Complete Solutions to Single Correct of chapter ELECTRIC POTENTIAL of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
A large insulated sphere of radius r charged with Q units of electricity is placed in contact with a small insulated uncharged sphere of radius r' and is then separated. The charge on the smaller sphere will now be.
View SolutionThree charges `2q, -q, and -q` are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionThe variation of potential with distance R from the fixed point is shown in (Fig. 3.125).
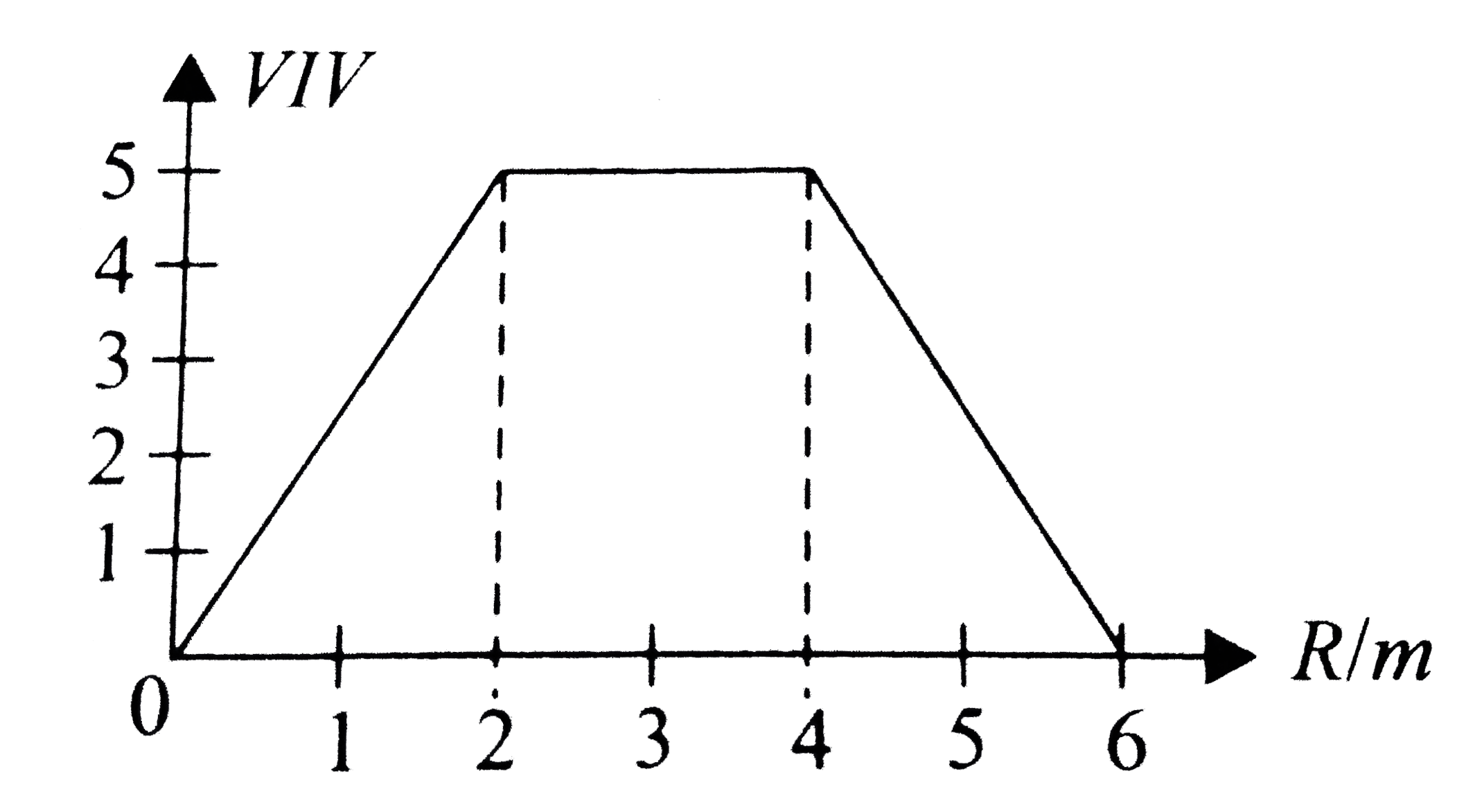 .
.
The electric field at `R = 5 m` is.
View SolutionWhen a `2 mu C` charge is carried from point A to point B, the amount of work done by the electric field is `50 mu J`. What is the potential difference and which point is at a higher potential ?
View SolutionThe work done in taking a unit positive charge from P to A is `W_A` and P to B is `W_B`. Then
 .
.
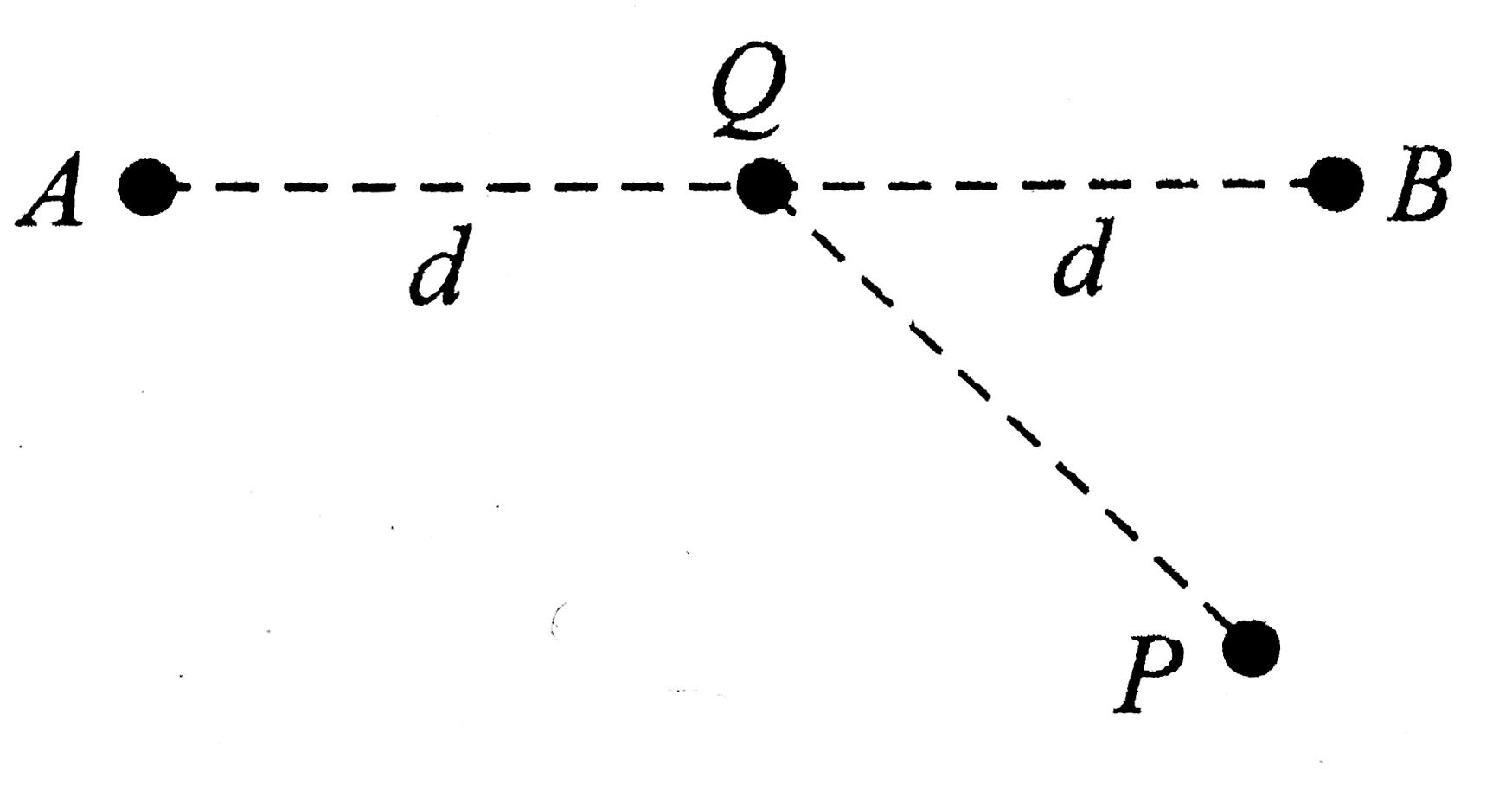
View SolutionThe electric field in a region surrounding the origin and along the x- axis is uniform. A small circle is drawn with the center at the origin cutting the axes at points `A, B, C, and D` having coordinates `(a,0),(0.a), (-a,0), and (0, -a)`, respectively, as shown in (Fig. 3.127). Then the potential is minimum at.
 .
.
View SolutionA small conducting sphere of radius a, carrying a charge `+Q`, is placed inside an equal and oppositely charged conducting shell of radius b such that their centers coincide. Determine the potential at a point which is at a distance c from center such that `a lt c lt b`.
View SolutionTwo metal spheres `("radii" r_1, r_2 "with" r_1 lt r_2)` are very far apart but are connected by a thin wire. If their combined charges is Q, then what is their common potential ?
View SolutionMark the correct statement :.
View SolutionVariation in potential is maximum if one goes.
View SolutionAn uncharged conductor A is brought near a positively charged conductor B. The size of the conductor A is much greater than the size of conductor B. Then,
View SolutionTwo spherical conductors of radii `R_1 and R_2` are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are `q_1 and q_2`, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .
.
View SolutionThree is an electric field E in the x - direction. If the work done by the electric field in moving a charge of `0.2 C` through a distance of `2 m` along a line making an angle `60^(@)` with the x- axis is `4 J`, then what is the value of E ?
View SolutionIn moving from A to B along an electric field line, the work done by the electric field on an electron is `6.4 xx 10^-19 J`. If `phi_1 and phi_2` are equipotential surfaces, then the potential difference `V_C - V_A ` is.
 .
.
View SolutionAn electron is taken from point A to point B along the path A B in a uniform electric field of intensity `E = 10 Vm^-1` side `AB = 5 m`, and side `BC = 3 m`. Then, the amount of work done on the electron by us is.
 .
.
View SolutionTwo identical rings `P and Q` of radius `0.1 m` are mounted coaxially at a distance `0.5 m` apart. The charges on the two rings are `2 mu C and 4 mu C`, respectively. The work done in transferring a charge of `5 mu C` from the center of P to that of Q is.
View Solution`n` charged drops, each of radius `r` and charge `q`, coalesce to from a big drop of radius `R` and charge `Q`. If `V` is the electric potential and `E` is the electric field at the surface of a drop, then.
View SolutionAt a point in space, the eletric field points toward north. In the region surrounding this point, the rate of change of potential will be zero along.
View SolutionA spherical charged conductor has surface density of charge as `sigma`. The electric field intensity on its surface is `E`. If the radius of the surface is doubled, keeping `sigma` uncharged, what will be the electric field intensity on the new sphere ?
View SolutionIn the previous question, if `V` is the electric potential of the first sphere, what would be the electric potential of the second sphere ?
View SolutionThe electric field lines are closer together near object `A` than they are near object `B`. We can conclude that.
View SolutionAs shown in figure a dust particle with mass m = 5.0 × 10–9 kg and charge q0 = 2.0 nC starts from rest at point a and moves in a straight line to point b . What is its speed v at point b?
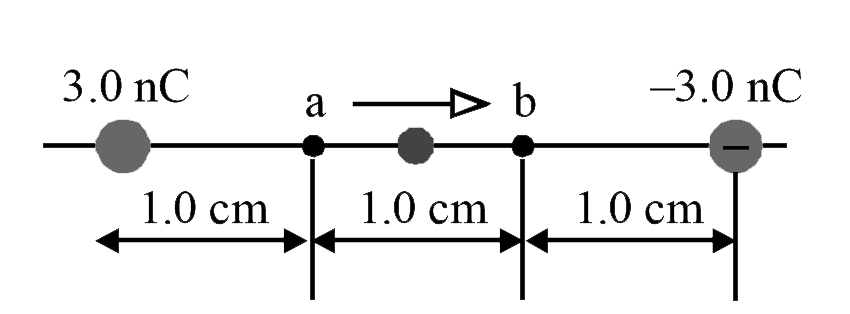
View SolutionCharges`-q , Q, and -q` are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio `Q//q`.
 .
.
View Solution`ABC` is a right - angled triangle, where `AB and BC` are `25 cm and 60 cm`, respectively. A metal sphere of `2 cm` radius charged to a potential of `9 xx 10^5 V` is placed at `B` as in (Fig. 3.133). Find the amount of work done in carrying a positive charge of 1 coulomb from C to A.
 .
.
View SolutionTwo charged particles having charges `1 and -1 mu C` and of mass `50 g` each are held at rest while their separation is `2 m`. Now the charges are released. Find the speed of the particles when their separation is `1 m`.
View SolutionAn electron is fired directly towards the center of a large metal plate that has excess negative charge with surface charge density `=2.0xx10^(-6) C//m^(2)`. If the initial kinetic energy of electron is 100 eV and if it is to stop due to repulsion just as it reaches the plate, how far from the plate must it be fired ?
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionFour identical charges are placed at the points `(1,0,0), (0,1,0),(-1,0,0)`, and `(0,-1,0)`. Then,
View SolutionWhen the separation between two charges is increase the electric potential energy of the charges.
View SolutionMark the correct statement :.
View SolutionTwo point charges `Q and -Q //4` placed along the x - axis are separated by a distance `r`. Take `-Q//4` as origin and it is placed at the right of Q. Then the potential is zero.
View SolutionThe electric potential decreases unifromly from 120 V to 80 V as one moves on the x-axis from x=-1 cm to x=+1 cm. The electric field at the origin
View SolutionA small sphere with mass `1.2 g` hangs by a thread between two parallel vertical plates `5.00 cm` apart. The plates are insulating and have uniform surface charge densities `+ sigma and - sigma`. The charge on the sphere is `q = 9 xx 10^-6 C`. What potential difference between the plates will cause the thread to assume an angle of `37^(@)` with the vertical as shown in (Fig. 3.134) ?
 .
.
View SolutionA particle of mass `m` carrying charge `q` is projected with velocity `v` from point `P` toward aninfinite line of charge from a distance `a` . Its speed reduces to zero momentarily at point `Q`, which is at a distance `a//2` from the line of charge. If another particle with mass `m` and charge `-q` is projected with the same velosity `v` from `P` toward the line of charge, what will be its speed at `Q` ?
View SolutionCharge `Q` is given a displacement `vec r = a hat i + b hat j` in an electric field `vec E = E_1 hat i + E_2 hat j`. The work done is.
View SolutionA point charge `q` is placed inside a conducting spherical shell of inner radius `2 R` and outer radius `3 R` at a distance of `R` from the center of the shell. Find the electric potential at the center of the shell.
View SolutionAn electric field is expressed as `vec E = 2 hat i + 3 hat j`. Find the potential difference `(V_A - V_B)` between two points `A` and `B` whose position vectors are given by `r_A = hat i + 2 hat j and r_B = 2 hat i + hat j + 3 hat k`.
View SolutionThe potentaial function of an electrostatic field is given by `V = 2 x^2`. Determine the electric field strength at the point `(2 m, 0, 3 m)`.
View SolutionA conducting sphere `A` of radius `a`, with charge `Q`, is placed concentrically inside a conducting shell `B` of radius `b`. `B` is earthed. `C` is the common center of `A and B`. Study the following statements.
(i) The potential at a distance `r` from `C`, where
`a le r le b, is (1)/(4 pi epsilon_0)(q/( r))`
(ii) The potential difference between `A and B` is
`(1)/(4 pi epsilon_0) Q ((1)/( r) - (1)/B)`
(iii) The potential at a distance `r` from `C`, where
`a le r le b, is (1)/(4 pi epsilon_0) Q ((1)/r - (1)/B)`
Which of the above statements are correct ?
 .
.
View SolutionAn electron having charge `e` and mass `m` starts from the lower plate of two metallic plates separated by a distance `d`. If the potential difference between the plates is `V`, the time taken by the electron to reach the upper plate is given by
 .
.
View SolutionThere is an infinite straight chain of alternating charges `q` and `-q` . The distance between teh neighbouring charges is equal to `a`. Find the interaction energy of each charge with all the others.
Instruction . Make use of the expansion of In `(1 + alpha)` in a power series in `alpha`.
View SolutionThree identical metallic uncharged spheres `A, B, and C,` each of radius `a`, are kept at the corners of an equilateral triangle of side `d(d gt gt a)` as shown in (Fig. 3.137). The fourth sphere (of radius a), which has a charge `q`, touches `A` and is then removed a position far away. `B` is earthed and then the earth connection is removed. `C` is then earthed. The charge on `C` is
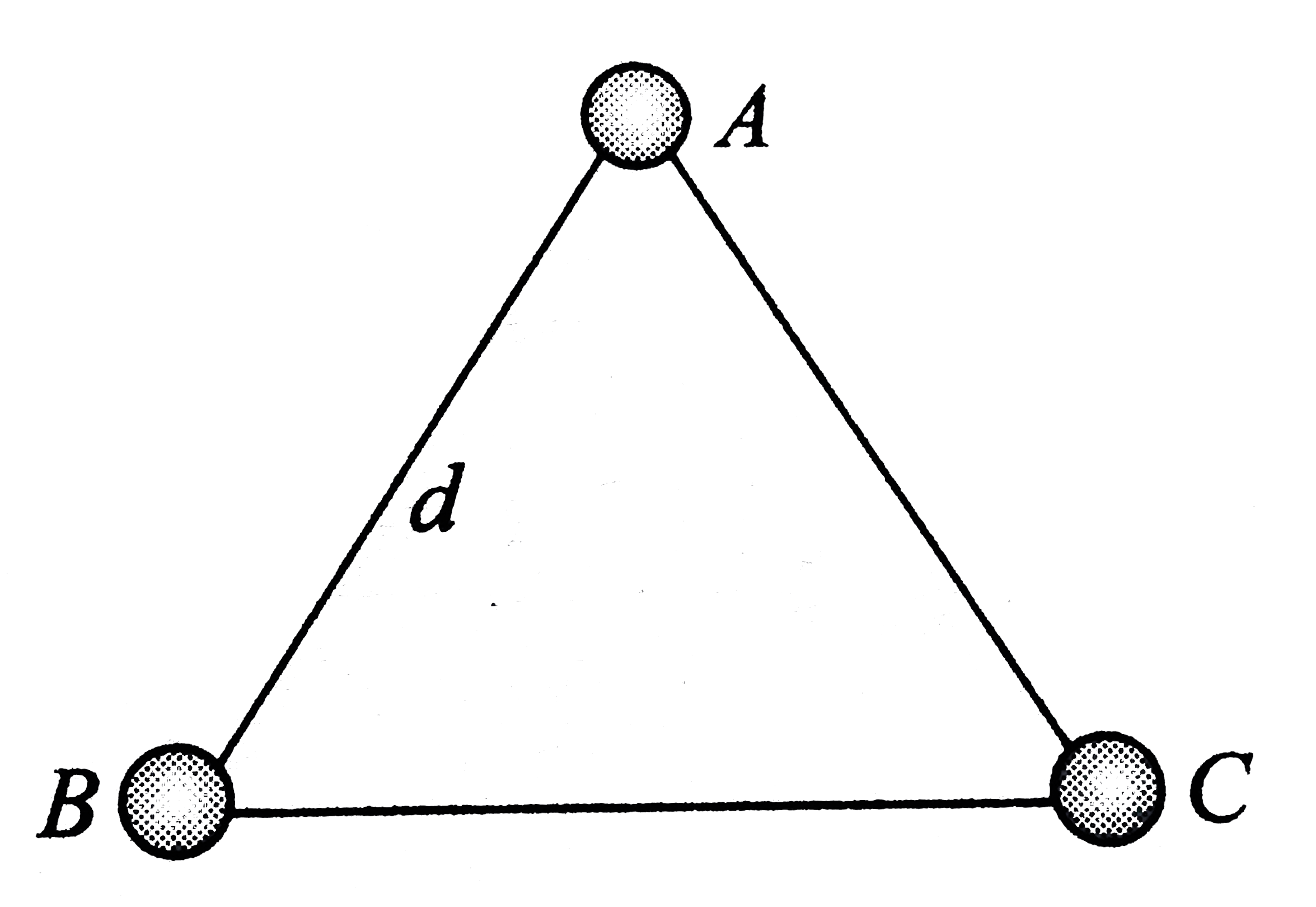 .
.
View SolutionA solid conducting sphere of radius `10 cm` is enclosed by a thin metallic shell of radius `20 cm`. A charge `q = 20 mu C` is given to the inner sphere is connected to the shell by a conducting wire.
View SolutionFind the potential `V` of an electrostatic field `vec E = a(y hat i + x hat j)`, where `a` is a constant.
View SolutionWe have three identical metallic spheres `A,B, and C`. `A` is given a charge `Q, and B and C` are uncharged. The following processes of touching of two spheres are carried out in succession. Each process is carried out with sufficient time. ltbgt i. A and B
ii. B and C
iii. C and A
iv. A and B
v. B and C
The final charges on the spheres are.
View SolutionDetermine the electric field strength vector if the potential of this field depends upon x - and y - coordinates as :
(i) `V = a(x^2 - y^2)`
(ii) `V = a x y`.
View SolutionThe point charge `q` is within the cavity of an electrically neutral conducting shell whose outer surface has spherical shape. Find the potential `V` at a point `P` lying outside the shell at distance `r` from the center `O` of the outer sphere.
 .
.
View SolutionTwo concentric conducting spherical shells of radii `a_1 and a_2 (a_2 gt a_1)` are charged to potentials `phi_1` and `phi_2`, respectively. Find the charge on the inner shell.
View Solution(Figure 3.139) shows three circular arcs, each of radius `R` and total charge as indicated. The net electric potential at the center of curvature.
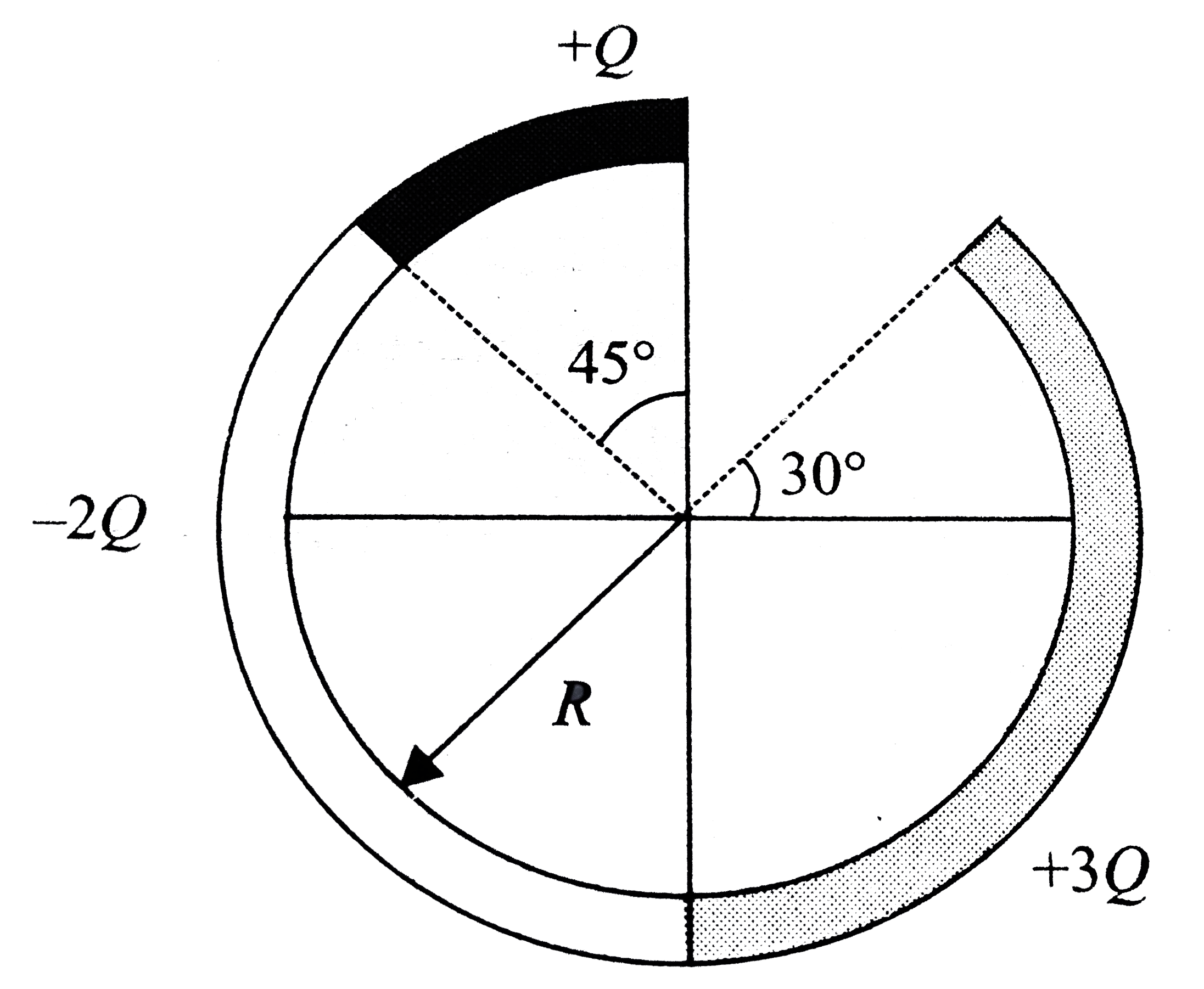 .
.
View SolutionWhen the positively charged hanging pendulum bob is made fixed, the work done in slowly shifting a unit positive charge from infinity to P is V. If the pendulum is free to move, the corresponding work done id `V'`. Then.
View SolutionThe potential V is varying with x as `V = (1)/(2) (y^2 - 4 x)` volt. The field at `x = 1m, y = 1 m,` is.
View SolutionA charge `+Q` at A (see Fig. 3.140) produces electric field `E` and electric potential V at D. If we now put charges `- 3 Q` and `+Q` at B and C, respectively, then the electric field and potential at `D` will be
 .
.
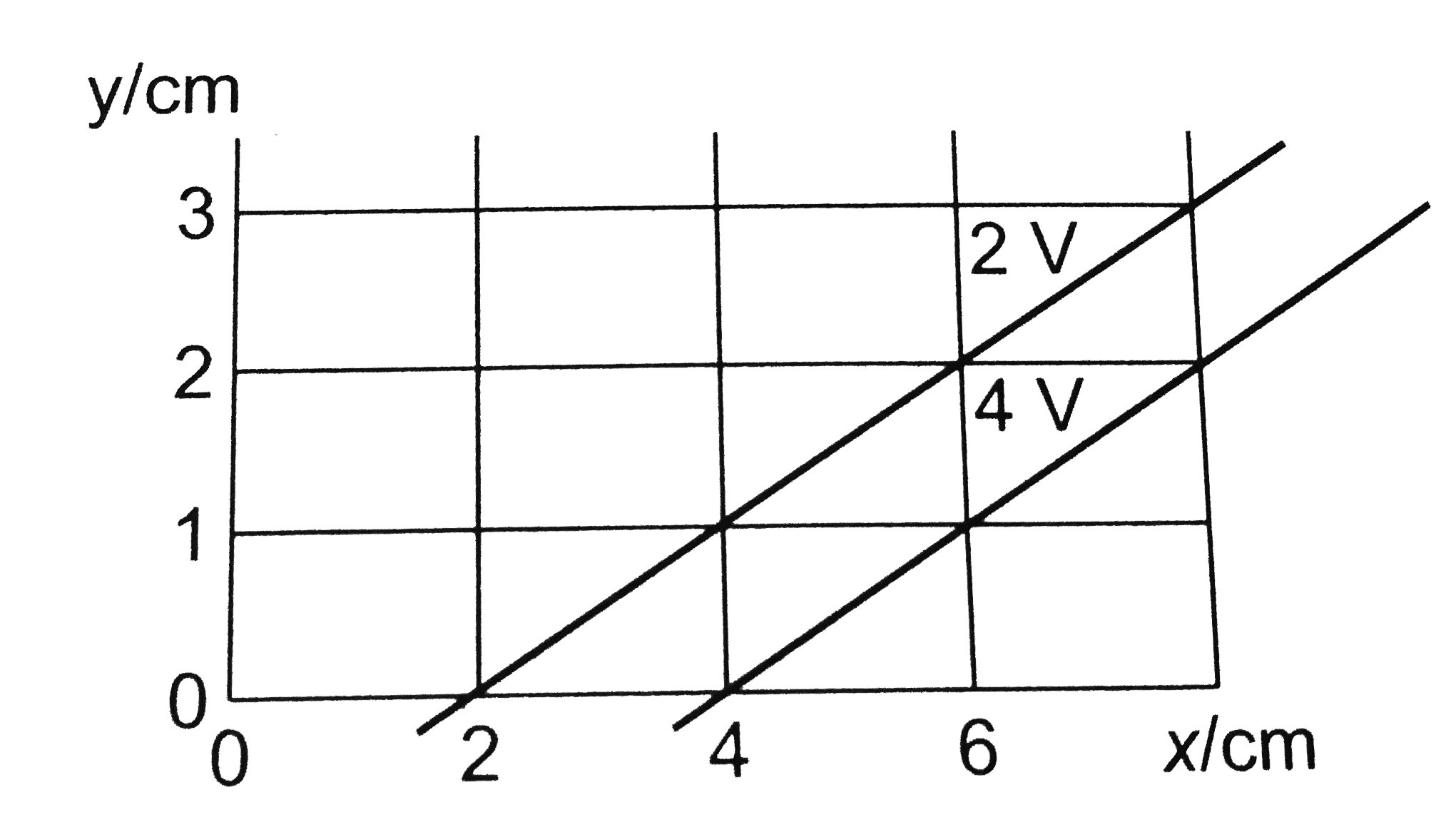
View SolutionFigure shown two equipotential lies `x, y` plane for an electric field. The scales are market. The `x`-component `E_(x)` and y-component `E_(y)` of the field in the space between these equipotential lines are respectively
View SolutionVariation of electrostatic potential along the x - direction is shown in (Fig. 3.142). The correct statement about electric field is
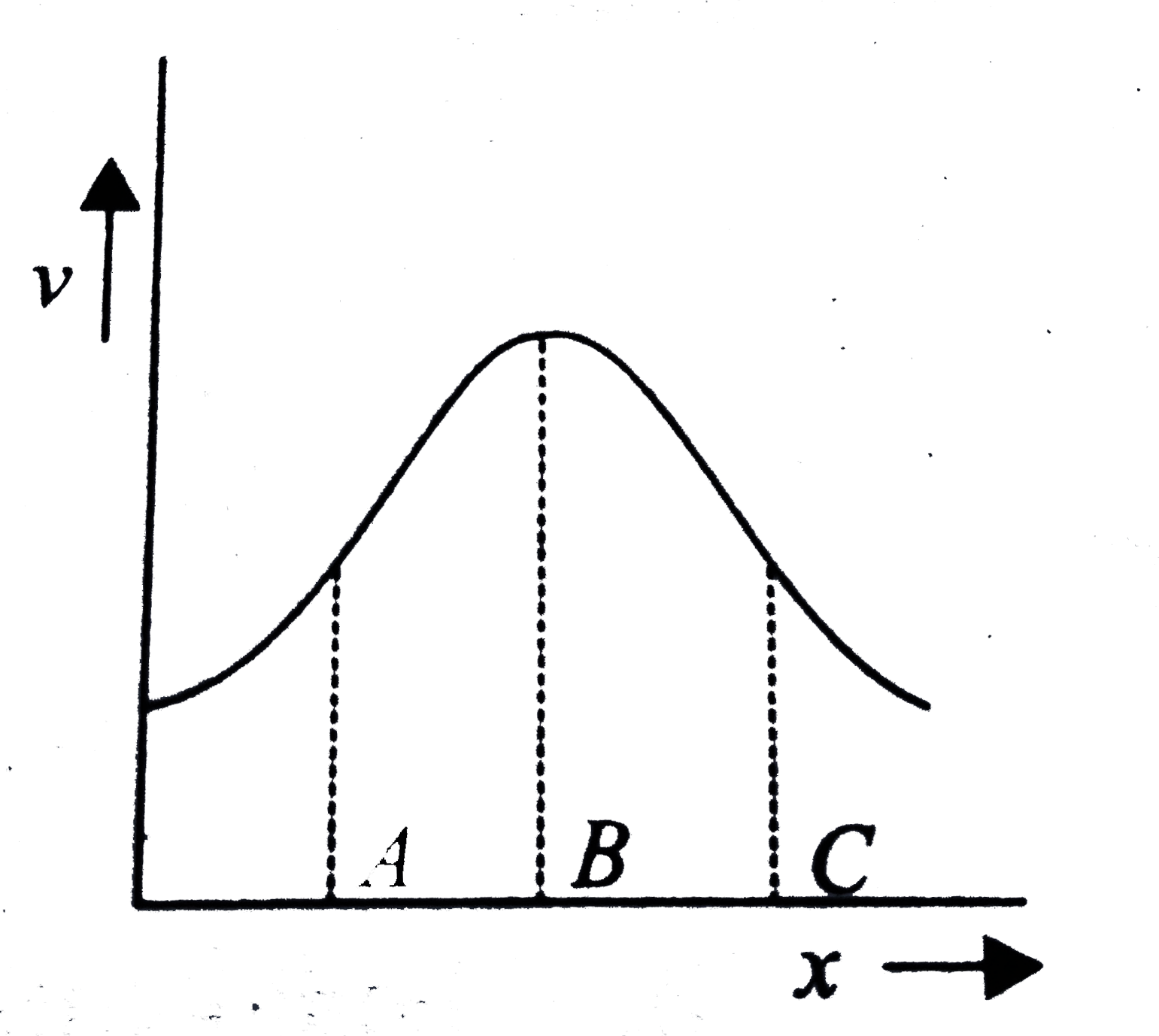 .
.
View SolutionA unit positive point charge of mass `m` is projected with a velocity `V` inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel is equal to

View SolutionElectric field given by the vector `vec E = x hat i + y hat j` is present in the x y plane. A small ring carrying `+Q`, which can freely slide on a smooth nonconducting rod, is projected along the rod from the point `(0, L)` such that it can reach the other end of the rod. What minimum velocity should be given to the ring ? (Assume zero gravity).
 .
.
View Solution
Single Correct questions and complete solutions for chapter ELECTRIC POTENTIAL of CENGAGE PHYSICS (HINGLISH) of Class 12