Complete Solutions to Illustration of chapter ELECTRIC POTENTIAL of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
find the work done by an external agent in slowly shifting a charge `q = 1 mu C` in the electric field ` vec E = 10^3 hat i Vm^-1` from the point `P(1,2) "to" Q(3, 4)`.
View SolutionA charge particle `q = -10 mu C` is carried along OP and PQ and then back to O along QO as shown in fig. 3 . 2, in an electric field `vec E = (x + 2y) hat i + 2x hat j` Find the work done by an external agent in (i) each path and (ii) the round trip.
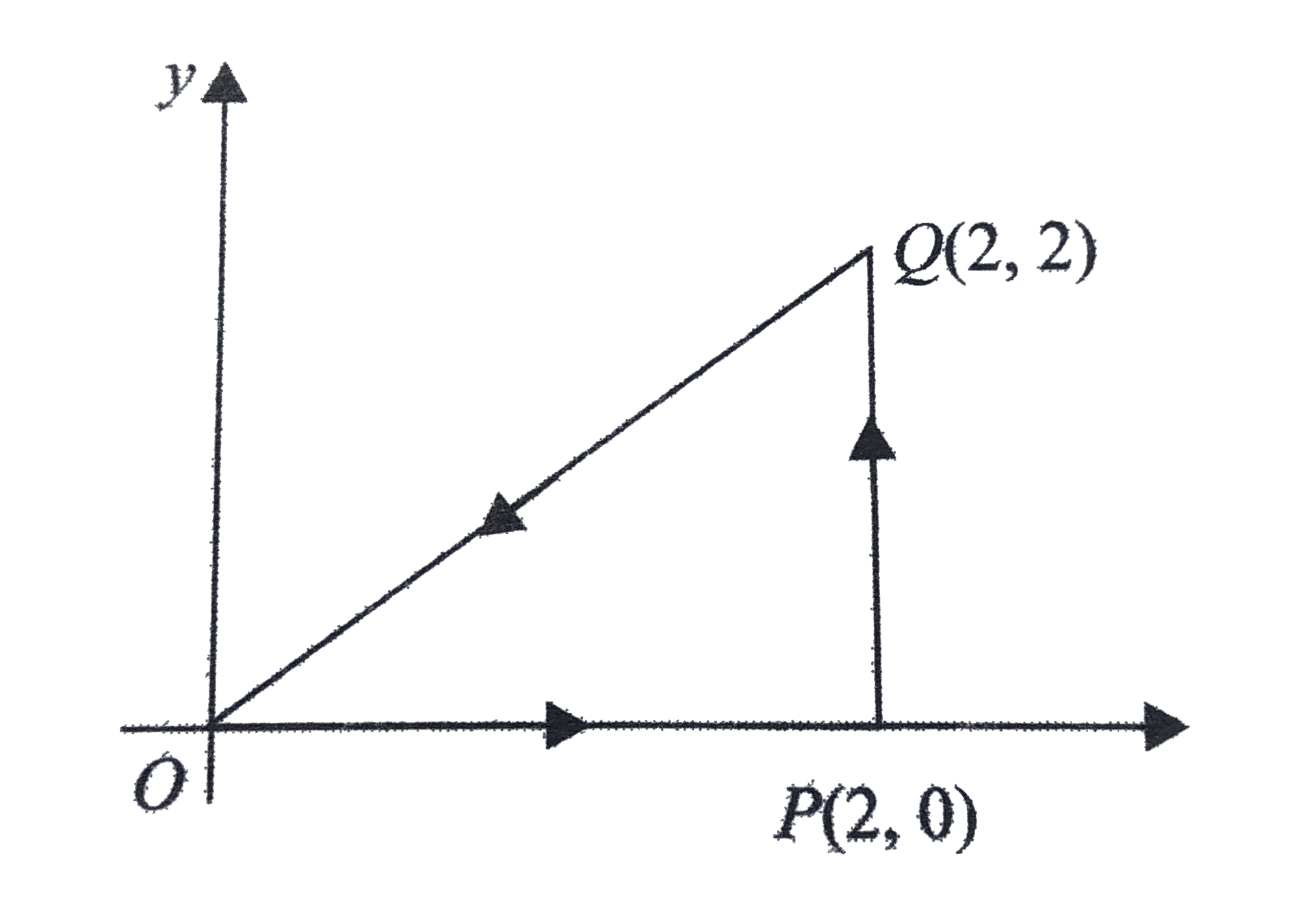 .
.
View SolutionThe electric field in a region is given by `vecE = (A/x^3) vecI.` Write a suitable SI unit for A. Write an experssion for. the potential in the region assuming the potential at. infinity to be zero.
View SolutionThree charges `q_1 = 1 mu C, q_2 = -2 mu C, and q_3 = -1 mu C` are placed at `A (0,0,0), B(-1 , 2,3,) and C (2 , -1, 1)`. Find the potential of the system of three charges at `P( 1, - 2, -1)`.
View SolutionTwo point charges `Q_1` and `Q_2` lie along a line at a distance from each other. Figure 3.7 shows the potential variation along the line of charges. At which of the points 1, 2, and 3 is the electric field zero ? What are the singns of the charges `Q_1` and `Q_2` and which of the two charges is greater in magnitude ?
 .
.
View SolutionTwo electric charges `q and - 2 q` are placed at a distance 6 m apart on a horizontal plane. Find the locus of point on this plane where the potential has a value zero.
 .
.
View Solution`1 mu C` charge is shifted from A to B, and it is found that work done by an external force is `40 mu J`. In doing so against electrostatic forces, find potential difference `V_A - V_B`.
View SolutionA uniform electric field is present in the positive x - direction. If the intensity of the field is `5 NC^-1` then find the potential difference `(V_B - V_A)` between two points A (0 m, 2 m) and B (5 m, 3 m).
View SolutionA uniform field of magnitude `vec E = 2000 NC^-1` is directed `theta = 37^(@)` below the horizontal [fig. 3.11].
 .
.
(i) Find the potential difference between P and R.
(ii) If we define the reference level of potential so that potential at R is `V_R = 500 V`, what is the potential at P?
View SolutionFind the potential difference `V_(AB)` between `A (0,0,0) and B (1 m , 1 m,1 m)` in an electric field :
(i) `vec E = (y hat i + x hat j) Vm^-1`
(ii) `vec E = (3 x^2 y hat i + x^3 hat j) Vm^-1`.
View SolutionUniform electric field of magnitude `100 Vm^-1` in space is directed along the line `y = 3 + x`. Find the potential difference between points `A (3,1) and B (1,3)`.
View SolutionA uniform electric field of magnitude `325 Vm^-1` is directed in the negative y - direction in (fig. 3.12). Theb coordinates of point A are `(-0.2 m , -0.3 m)` and those of point B are `(0.4 m, 0.5 m)`. Calculate the potential difference `V_B - V_A` along the path shown in the figure.
 .
.
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to `a//2`.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side `2 a`.
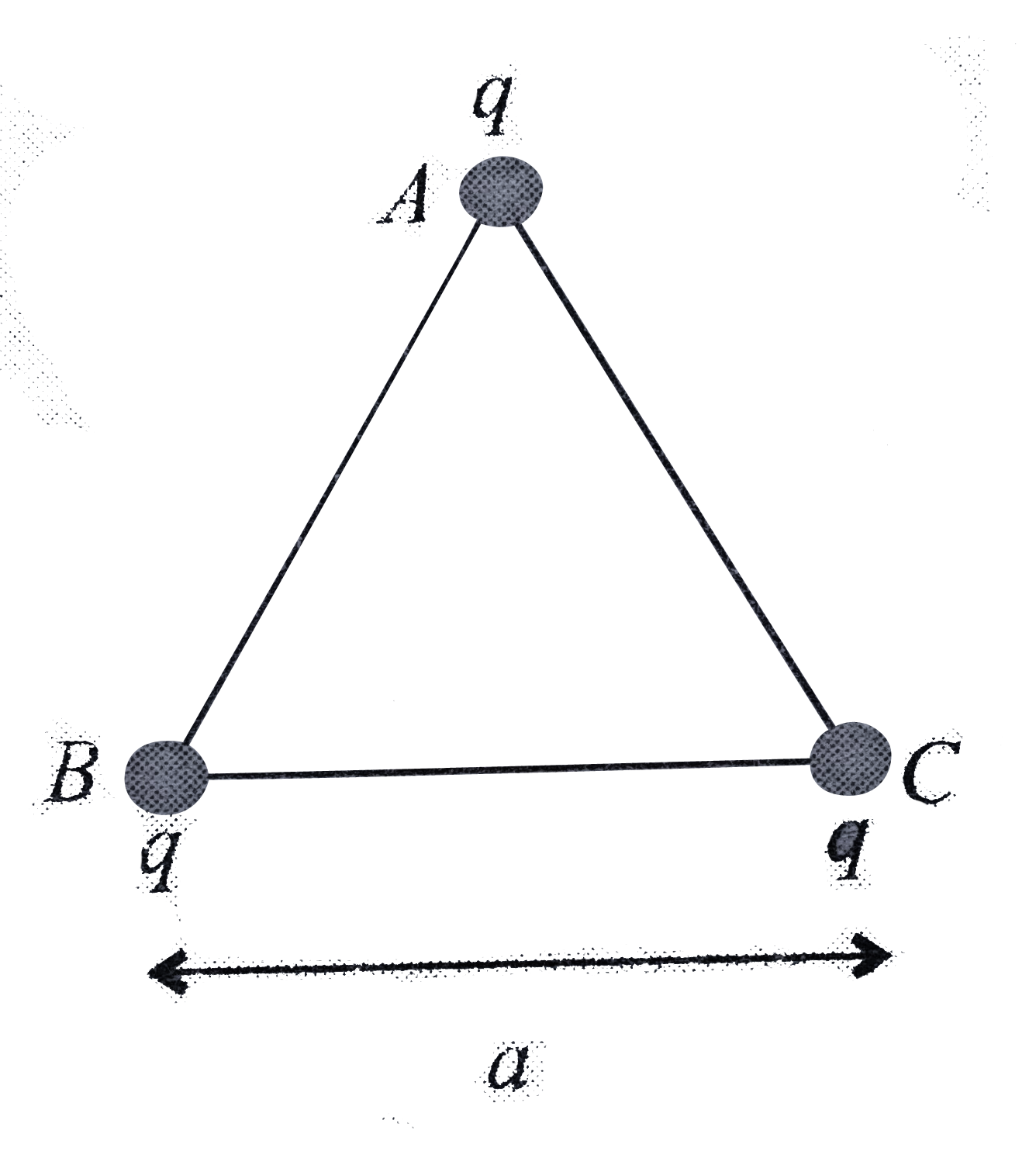 .
.
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionAn alpha particle with kinetic energy `10 Me V` is heading toward a stationary tin nuclcus of atomic number 50. Calculate the distance of closest approach (Fig . 3.23).
 .
.
View SolutionA proton moves from a large distance with a speed u m/s directly towards a free proton originally at rest. Find the distance of closest of closest approach for the two protons in terms of mass of proton m and its charge e.
View SolutionIn space of horizontal `EF (E = (mg)//q)` exist as shown in figure and a mass m is released at the end of a light rod. If mass m is releases from the position shown in figure find the angular velocity of the rod when it passes through the bottom most position
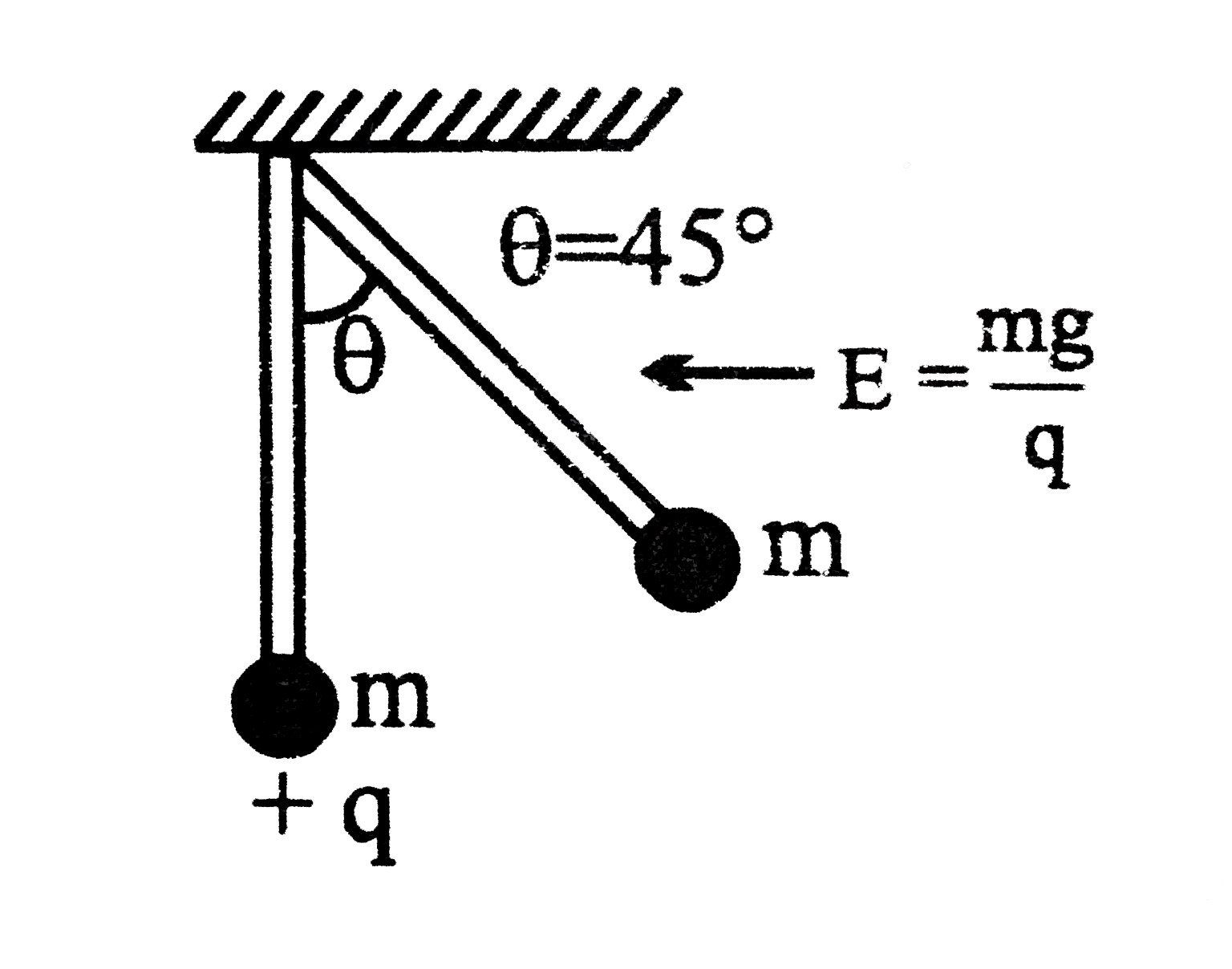 .
.
View Solution(Figure 3.27) shows equipotential surfaces. What is the direction of electric field `vec E` at P and R?
 .
.
View SolutionThree equipotential surfaces are shown in (Fig. 3.28) A. Draw the corresponding field lines and estimate the field strength at a point A where the distance between the surfaces is 4 cm.
a.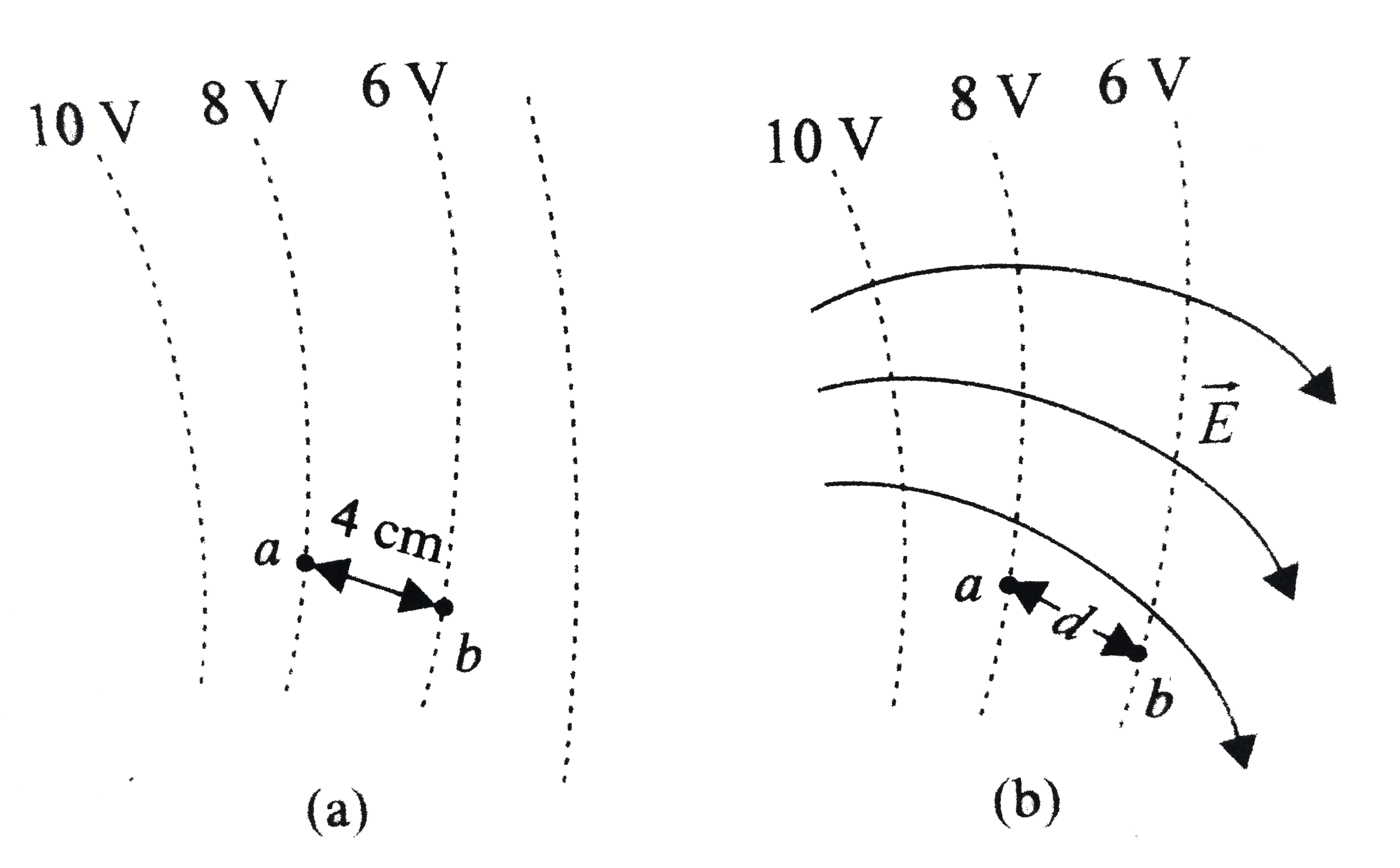
View SolutionConsider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionThe potential at any point is given by `V = x(y^2 - 4 x^2)`. Calculate the cartesian components of the electric field at the point.
View SolutionSome equipotentialo surfaces are shown in (Fig. 3.31.) What can you say about the magnitude and the direction of the electric field ?
 .
.
View SolutionDetermine the electric field strength vector if the potential of this field depends upon x - and y - coordinates as :
(i) `V = a(x^2 - y^2)`
(ii) `V = a x y`.
View Solution(i) Find the field intensity if potential `V = - k x y (k gt 0)`.
(ii) Draw the field pattern of the field in i.
View SolutionA, B, C, D, P, and Q are points in a uniform electric field. The potentials at these points are `V(A) = 2 V. V(P) = V( B) = V(D) = 5 V`, and `V(C) = 8 V`. Find the electric field at P.
 .
.
View SolutionReferring to the spherical equipotential lines in (Fig. 3.36)A, find
(i) `vec E = f ( r)`
(ii) `vec E` - pattern.
a. .
.
b. .
.
c. .
.
View SolutionA very small sphere of mass `80 g` having a charge q is held at a height of `9 m` vertically above the center of a fixed conducting sphere of radius `1 m`, carrying an equal charge q. When released, it falls until it is repelled back just before it comes in contact with the shpere as shown in Fig. 47. Calculate the charge `q. [g = 10 ms^-2]`.
View SolutionA hollow uncharged spherical conductor has inner radius A and outer radius b. A positive point charge +q is in the cavity at the center of the sphere (Fig. 3.48). Find the potential V( r) everywhere, assuming that `V = 0` at `r rarr oo`.
 .
.
View Solution(Figure 3.51) shows two concentric conducting shells of radii `r_(1)` and `r_(2)` carrying uniformaly distributed charges `q_(1)` and `q_(2)`, respectively. Find an expression for the poptential of each the potential of each shell.
 .
.
View SolutionA metal sphere A of radius a is charged to potential V. What will be its potential if it is enclosed ny a spherical conducting shell B of radius b and the two are connected by a wire ?
View SolutionFind the electric work done in bringing a charge q from A to B in a sphere of charge Q distributed uniformly throughout its volume.
 .
.
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance `r (r gt R)` from the center of the sphere. Find the minimum velocity v so that it can penetrate `(R//2)` distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View SolutionA charge particle q is shifted from point 1 to point 2 in the electric field of a straight long linear charge of `lambda`.
i. Find the electric work done if `r_1 = R` and `r_2 = 2 R`
ii. Find the potential difference between 1 and 2.
 .
.
View SolutionTwo circular loops of radii `0.05` and `0.09 m`, respectively, are put such that their axes coincide and their centers are `0.12 m` apart. A charge of `10^-6 C` is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View SolutionA circular ring of radius R with uniform positive charge density `lambda` per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point `p( - sqrt(3) R, 0,0)` on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA spherical shell of radius `R_(1)` with uniform charge q is expanded to a radius `R_(2)`. Find the work performed by the electric forces in this process.
View SolutionA spherical shell of radius `R_(1)` with a uniform charge q has a point charge `q_0` at its center. Find the work performed by the electric forces during the shell expansion from radius `R_(1)` to radius `R_(2)`.
View SolutionInside a conducting hollow sphere of inner radius `R_(1)` and outer radius `R_(2)`, a point charge q is placed at a distance `x` from the center as shown in (Fig. 3.70.) Find.
 .
.
(i) electric potential at C
(ii) electric field and potential at a distance r from the center outside the shell.
View SolutionIn (Fig. 3.73), if the inner shell has charge `+q_0` and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionConsider two concentric spherical metal shells of radii `'a'` and `bgt a` .The outer shell has charge `Q` but the inner shell has no charge.Now the inner shell is grounded ,This means that the inner shell will come at zero potential and that electric fields lines leave the outer shell and end on the inner shell.(a) Find the charge on the inner shell
Find the potential on outer sphere.

View Solution(Figure 3.78) shows three thin concentric spherical shells A, B and C with initial charges on A , B, and C as 3 Q, 2Q, and -Q, respectively. The shells A amd C are connected by a wire such that it does not touch B. Shell B is earthed. Determine the final charges `q_A, q_B, "and" q_C`.
 .
.
View SolutionTwo small particles A and B having masses `m = 0.5 kg` each and charges `q_1 = (-155//18 muC)` and `q_2 = (+100 muC)`, respectively, are connected at the ends of a nonconducting, flexible, and inextensible string of length `r = 0.5 m`.
Particle A is fixed and B is whirled along a verticle circle with center at A. if a vertically ipward electric field of Strength `E = 1.1 xx 10^5 NC^-1` exists in the space, calculate the minimum velocity of particle B required at the highest point so that it may just complete the circle `(g = 10 ms^-2)`.
 .
.
View SolutionA small sphere of mass `m = 0.6 kg` carrying a positive charge `q = 80 muC` is connected with a light, flexible, and inextensible string of length `r = 30 cm` and whirled in a vertical circle. If a horizontal rightward electric field of strength `E = 10^5 NC^-1` exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle `(g = 10 ms^-2)`.
View SolutionTwo point charges of `3.2 xx 10^-19 C and -3.2 xx 10^-19 C` are separated from each other by `2.4 xx 10^-10 m`. The dipole is situated in a uniform electric field of intensity `4 xx 10^5 Vm^-1`. Calculate the work done in roating the dipole by `180^(@)`.
View SolutionWhat is the potential energy of the charge and dipole system shown in (Fig. 3.93) ?
 .
.
View Solution
Illustration questions and complete solutions for chapter ELECTRIC POTENTIAL of CENGAGE PHYSICS (HINGLISH) of Class 12