Complete Solutions to Exercises (integer) of chapter INDUCTANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INDUCTANCE |
| CENGAGE PHYSICS | Exercises (integer) |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Figure shows a part of a bigger circuit. The capacity of the capacitor is `6 mF` and is desaesing at the constate rate `0.5 mF s^(-1)`. The potential difference across the capacitor at the shows moment is changing as follows:
`(dV)/(dt) = 2 V s^(-1)`, `(d^(2)V)/(dt^(2)) = (1)/(2) V S^(-2)`
The current in the `4 Omega` resistor is decreasing at the rate of `1 mA s^(-1)`. What is the potential difference (in `mV`) across the inductor at this moment?

View SolutionIn the circuit (Fig.) what is potential difference `V_(B) - V_(A)` (in `V`) when current `I` is `5 A` and is decreasing at the rate of `10^(3) A s^(-1)`
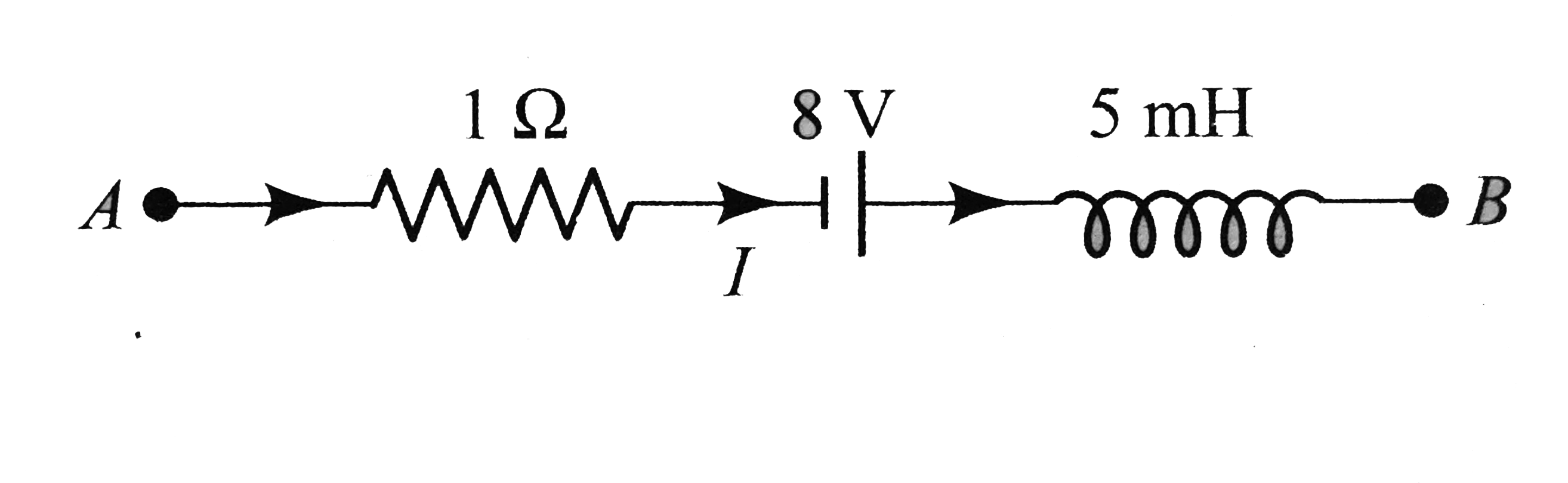
View SolutionA current of `2 A` is increasing at a rate of `4 A s^(-1)` through a coil of inductance `1 H`. Find the energy stored in the inductor per unit time in the units of `J s^(-1)`.
View SolutionFigure shows a circuit having a coil of resistance `R = 2.5 Omega` and inductance `L` connected to a conducting rod of radius `10 cm` with its center at `P`.

Assume that friction and gravity are absent and a constant uniform magnatic field of `5 T` exists as shown in figure. At `t = 0`, the circuit is switched on and simultaneously a time-varying external torque is applied on the rod so that it rotates about `P` with a constant angular velocity `40 rad s^(-1)`. Find the magnitude of this torque (in `mNm`) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.
View SolutionIn the given circuit, initially switch `S_(1)` is closed, and `S_(2)` and `S_(3)` are open. After charging of capacitor, at `t = 0`, `S_(1)` is opened and `S_(2)` and `S_(3)` are closed. If the relation between inductance, capacitance and resistance is `L = 4 CR^(2)`, tehn find the time (in s) after which current passing through capacitor and inductor will be same (given `R = In2 m Omega,L = 2 mH`)

View SolutionTwo colis, `1` and `2` have a mutual inductance `M = 5H` and resistance `R = 10 Omega` each. A current flows in coil 1, which varies with time as: `I_(1) = 2t^(2)`, where `t` is time. Find the total charge (in `C`) that has flows through coil `2` between `t = 0` and `t = 2 s`.
View SolutionA long solenoid of diameter `0.1 m` has `2 xx 10^(4)` turns per metre. At the centre of the solenoid, a `100-`turns coil of radius `0.01 m` is placed with its axis coinciding with the constant rate from `+ 2 A` to `2 A` in `0.05 s`. Find the total charge (in `mu C`) flowing through the coil during this time when the resistance of the coil is `40 !=^(2) Omega`.
View SolutionA capacitor of capacity `2 muF` is charged to a potential difference of `12 V`. It is then connected across an inductor of inductance `6 mu H`. What is the current (in `A`) in the circuit at a time when the potential difference across the capacitor is `6.0 V`?
View Solution
Exercises (integer) questions and complete solutions for chapter INDUCTANCE of CENGAGE PHYSICS (HINGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS INDUCTANCE
- Archives (fills In The Blanks)
- Archives (integer)
- Archives (linked Compreshension)
- Archives (multiple Correct)
- Archives (single Correct )
- Comprehension Type
- Concept Based
- Exercise 4.1
- Exercises (assertion-reasoning)
- Exercises (integer)
- Exercises (linked Compreshension)
- Exercises (multiple Correct )
- Exercises (single Correct )
- Exercises (subjective)
- Illustration
- Multiple Correct Answer
- Single correct Answer Type
- Solved Examples
- Subective Type