Complete Solutions to QUESTION BANK of chapter ELECTROMAGENTIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGENTIC INDUCTION |
| CENGAGE PHYSICS | QUESTION BANK |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
A flat, circular coil of radius `10 cm` has 100 turns of wire. Auniform magnetic field exists in a direction perpendicular to the plane of the coil. This ficld is increasing at the rate of `0.1 T / s`. Calculate the magnitude of emf induced (in volt) in the coil.
View SolutionA wire loop of area `0.2 m^(2)` has a resistance of `20 ohm . (A)` magnetic field, normal to the loop, initially has a magnifude of `0.25 T` and is reduced to zero at a uniform rate in `10^(-4) s`. Estimate the resulting current in ampere.
View SolutionA long solenoid has 1000 turns. When a current of `4 A` flows through it, the magnetic flux linked with each tum of the solenoid is `4 times 10^(-3) (wb)`. The self-inductance (in henry) of the solenoid is
View SolutionA condacting circular loop is placed in a uniform magnetic field `0.04T` with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at `2 mm / s`. The indaced emf in the loop whicn the redius is `2 cm` is `y pi` microvolt, then find `y`.
View SolutionA coil having 30 tums of wire, each of area' `10 cm^(2)`, is placed with its plane at rigiht angle to a magnetic ficld of `0.1 T`. When the coil is suddenly withdrawn from the field, a gaivanometer in series with the coil indicates that a charge of `10^(-5)C` passes around the circuit. What is the combined resistânce (in ohm) of the coil and the galvanometer?
View SolutionA metal dise of radins `0.1m` spins about a horizontal axis lyinig in the magnetic meridian' at a speed of 5 revis. If the horizontal componeat of the earth's.field is `B=2 xx 10^(-5) Wb / m^2`, the potential difference between the centre and the outer edge of the disc is `zxx 10^(-6) V` Find `z`.
View SolutionIn a coil of resistance `10 ohm`, the induced current developed by changing magnetic flux through it is shown in figure as a function of time. The magnitade of change in flux (in weber) through the coil is
'(##CEN_KSR_PHY_JEE_CO23_E01_007_Q01##)'
View SolutionA body enters in an MRI machine in `10 s`. If the magnctic field is `1.5 T` and circumference of the MRI mechine is `0.9 m`, then find out the magnitude of emf induced (in milli volt) in the body.
View SolutionA long solenoid of radius `2cm` has `100 (turns) / (cm)` and carries a current of `5A`. A coil of radius `1 cm` having 100 tums and a total resistance of `20 ohm` is placed inside the solenoid coraxially, The coil is cornected to a galwanometer and the current in the solenoid is reversed in direction. If the charge flown through the galvanometer is `k times 10^(-oo) C`, then find `k`. (Take `pi^(2)=10` )
View SolutionIn an R-I circuit, `R=4 ohm, L=0.5 (H)` and emf of cell `=6V. The work done (in mj ) in changing the current from `0.80A to `0.81A` through the circuit is
View SolutionA long solenoid of diameter `0.1 m` has `2xx 10^(4)` turns per metre. At the centre of the solenoid, a coil of 100 turns and radius `0.01 m` is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to `0 A` from `4A` in `0.05` .If the resistance of the coil is `10 pi^(2) ohm`, the total charge (in `mu C` ) flowing through the coil during this time is
View SolutionA small piece of metal `(mu_(r) = 20 )`of volume `10 cm ^3` has a uniform magnetie field 4T` inside it, Thé magnetic eneigy stored in the metal is `(alpha)/(pi) J_(3)` then find `alpha`.
View SolutionA solenoid having 500 turns and length `2m` has radius of 2 cm. Then self-inductance (in milithenry) of solenoid is
View SolutionA simple electric motor has an armature resistance of `1Omega` and runs from a dc source of 12 volt . When running unloaded it draws a current of 2 amp . When a certain load is connected , its speed becomes one-half of its unloaded value . The new value of current drawn
View SolutionIn an ac dynamo, the peak value of emf is `60V`. The induced emf (in V) in the position when the armature makes an angle of `30^(circ)` with the magnetic ficld perpendicular to the coil, will be
View SolutionAn electric motor operating on a `60 V` dc supply draws a currrent of `10A`. If the effeciency of the motor is `50%`, the resistance of its winding is
View SolutionThe time constunt of an `L-R` circuit is `10 s`. When a resistance of `10 ohm` is connected in series in a previous circuit, then the time constant becomes. `2s`. The self-inductance (in henry) of the circuit is
View SolutionA square of side `L` meters lies in the `x-y` plane in a region where tbe magnctic fleld is given by `vec(B)=B_(0)(2 hat(i)+3 hat(j)+4 hat(k))` tesla `_(3)` where `B_(0)` is a constant. If the magnitude of flux passing through the square is `y B_(a) L^(2)` weber, then find the value of `y .`
View SolutionA `10 (~V)` battery, conmected to `5 ohm` resistance coil having inductance 10 H ` through a switch, drives a constant carrent in the circuit, The switch is saddenly opened and the time taken to open it is `2 ms `. If the average emf induced across the coil is `varepsilon`, then find `(E)/(1000)`.
View SolutionA wooden stick of length `3 l` is rotated ahout an end with constant angular velocity `ohm` in a uniform magnetic ficld `underline(B)` pérpendicular to the plane of motion. If the upper oaethird of its length is coated with copper, the potential. difference across the whole length of the stick is `(x B ohm l^(2))/(2)`. Find `x`.
'(##CEN_KSR_PHY_JEE_CO23_E01_020_Q02##)'
View SolutionA physicist works in a laboratory where the magnetic field 'is 2T`. She wears a necklace of enclosing are `0.01 m^2` in such a way that the plane of the necklace is norinal to the field and is having a resistance `R=0.01 ohm`. Because of power failure, the field decays to 1 ' `T` in time `10^(-1)s`. Then what is the total beat produced (in joule) in her necklace?
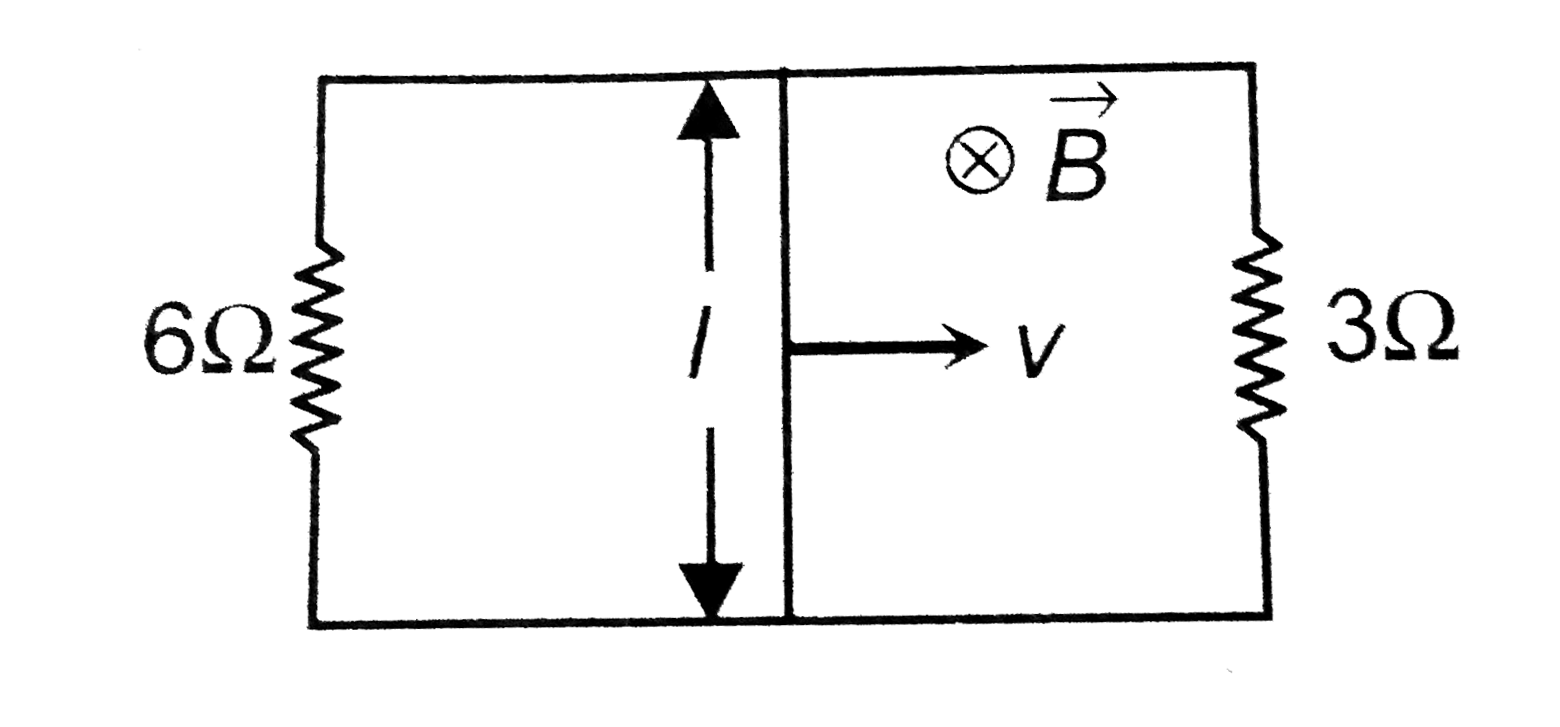
View SolutionThe network shown in the figure is a part of a copmplete circuit. If at a certain instant, the current `i` is `5A` and decreasing at the rate of `10^(3) A / s`, then `V_(s)-V_(A)` (in volt) is
'(##CEN_KSR_PHY_JEE_CO23_E01_022_Q03##)'
View SolutionA conducitng rod `AB` of length `l = 1 m` moving at a velcity `v = 4 m//s` making an angle `30^(@)` with its length. A uniform magnetic field `B = 2T` exists in a direction perpendicular to the plane of motion. Then :

View SolutionA wire is sliding on two parallel conducting rails placed at a separation of `1m` as shown in the figure."Magnetic field of `2T` exists in a directịon perpendicular to the rails. The necessary force required to keep the wire moving with a constant velocity of `1 cm /s` is `pi xx10^(-4) N`. Find `n .`
View SolutionThe below figure shows a circuit that contains threc identical resistors with resistance `R=9.0 ohm` each, two identical inductors with inductance `L=2.0mH` each, and an ideal battery with emf `varepsilon=18 V`. The current `i` (in ampere) through the bettery just after the switch is closed,
View SolutionA copper disc of radius `10cm` is rotating in magnetic field `B=0.4 G` with `10 rev /s`. What will be the potential differenee across the peripheral points of disc?
View SolutionAn inductor `(L=100 mH)`, a resistor `(R=100 ohm)` and a battery `(E=100 V)` are. initially connected in series as shown in the figure. Afler a long time, the battery is disconnected after short-circuiting the points `A` and `B`. The current in the circuit, `1 ms` after the short-circuit, is `(k)/(4)`. Find `k`.
View SolutionA loop made of straight edegs has six corners at `A(0,0,0), B(L, O,0) C(L,L,0), D(0,L,0) E(0,L,L)` and `F(0,0,L)`. Where `L` is in meter. A magnetic field `B = B_(0)(hat(i) + hat(k))T` is present in the region. The flux passing through the loop `ABCDEFA` (in that order) is
View SolutionA rectangular loop of sides `8cm` and `2 cm` with a small cut is moving out of a region of uniform magnetic field of magnitude `0.3` T directed normal to the loop. The velocity of the loop is `1cm s^(-1)` in the direction normal 'to the (i) longer side, (ii) shorter side of the loop. If the ratio of voltage induced in case (i) to case (ii) is `alpha` and the ratio of time for which voltage induced in case (ti) to case (i) is `beta`, then calculate `(alpha times beta)`.
View SolutionIn the given circuit, the ratio of `(t)_(1)` to `i_(2)` is `(x)/(y)`, where `i_(1)` is the initial (at `t=0` ) current and `i_(2)` is steady state (at `t=oo` ) current through the battery. Find `(x+y)`.
'(##CEN_KSR_PHY_JEE_CO23_E01_030_Q09##)'
View SolutionA rectangle loop with a sliding connector of length `l=1.0 m` is situated in a uniform magnetic field `B=2T` perpendicular to the plane of loop. Resistance of connector is `r=2Omega`. Two resistance of `6Omega` and `3Omega` are connected as shown in figure. the external force required to keep the connector moving with a constant velocity `v=2m//s` is
View SolutionAn inductor coil stores 32 J of magnetic field energy and dissiopates energy as heat at the rate of 320 W when a current of 4 A is passed through it. Find the time constant of the circuit when this coil is joined across on ideal battery.
View SolutionA time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)

View SolutionThe ratio of time constant in charging and discharging in the circuit shown in the figure is `(x)/(y)`. Find `(x+y)`
'(##CEN_KSR_PHY_JEE_CO23_E01_034_Q12##)'
View SolutionThe magnetic flux through a stationary loop with a resistanoe `R` varies during interval of time `T` as `phi=` at `(T-`t). If the heat generated during this time, neglecting the inductance of the loop, is `(a^(2) T^(3))/(p R)`, then find `p`.
View SolutionAs shown in the figare, wire `P Q` has negligible resistance. `B`, the magnetic field, is coming out of the paper, `theta` is a fixed angle mede by `P Q` travelling smoothly over two condiucting parallel wires separated by a distance `d`, If the current in the wirc for the configuration is `I=(x d V B)/(4 R)`, then find `x`.
'(##CEN_KSR_PHY_JEE_CO23_E01_036_Q13##)'
View SolutionThere are two coils `A` and `B` separated by some distance. If a curreat of 2 A flows through `A`, a magnetic flux of `10^(-2) Wb` passes through `B` (no current through B ). If no current passes through `A` and 'a current of 1 A.passes through `B`, then what is the flux (in `(mWb)` ) through A ?
View SolutionThe induced emf in the loop, if the long wire carries a current of `50 A` and the loop has an instantaneous velocity `v=10 m / s` at the location `x=0,2m` as shown in figure is e microvolt. Caluclate `3 epsilon` (Take `a=0.1m`)
'(##CEN_KSR_PHY_JEE_CO23_E01_038_Q14##)'
View SolutionA small square loop of wire of side `l` is placed inside a large square loop of wire of side `(L gt gt l)`. The loops are coplanar and their centres coincide. If the mutual inductance of the system is `p sqrt(q) (mu_(0))/(pi) (l^(2))/(L)`, then find `(p+q)`.
View SolutionA square wire of length `L_(1)` mass `m` and resistance `R` slides without friction on parallel conducting resistanceless rails. The rails are interconinected at the bottom by resistanceless rails so that the wire and the rails form a closed rectangular loop. The plane of the rails is inclined at an angle `theta` with the horizontal and a vertical uniform magnetic field `B` exists within the frame. If the wire acquires a steady velocity of magnitude `v=(k m g R sin theta)/(6 B^(2) l^(2))`, `cos ^(2) theta`
'(##CEN_KSR_PHY_JEE_CO23_E01_040_Q15##)'
View Solution
QUESTION BANK questions and complete solutions for chapter ELECTROMAGENTIC INDUCTION of CENGAGE PHYSICS (HINGLISH) of Class 12