Complete Solutions to Level 2 Subjective of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| DC PANDEY | Level 2 Subjective |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
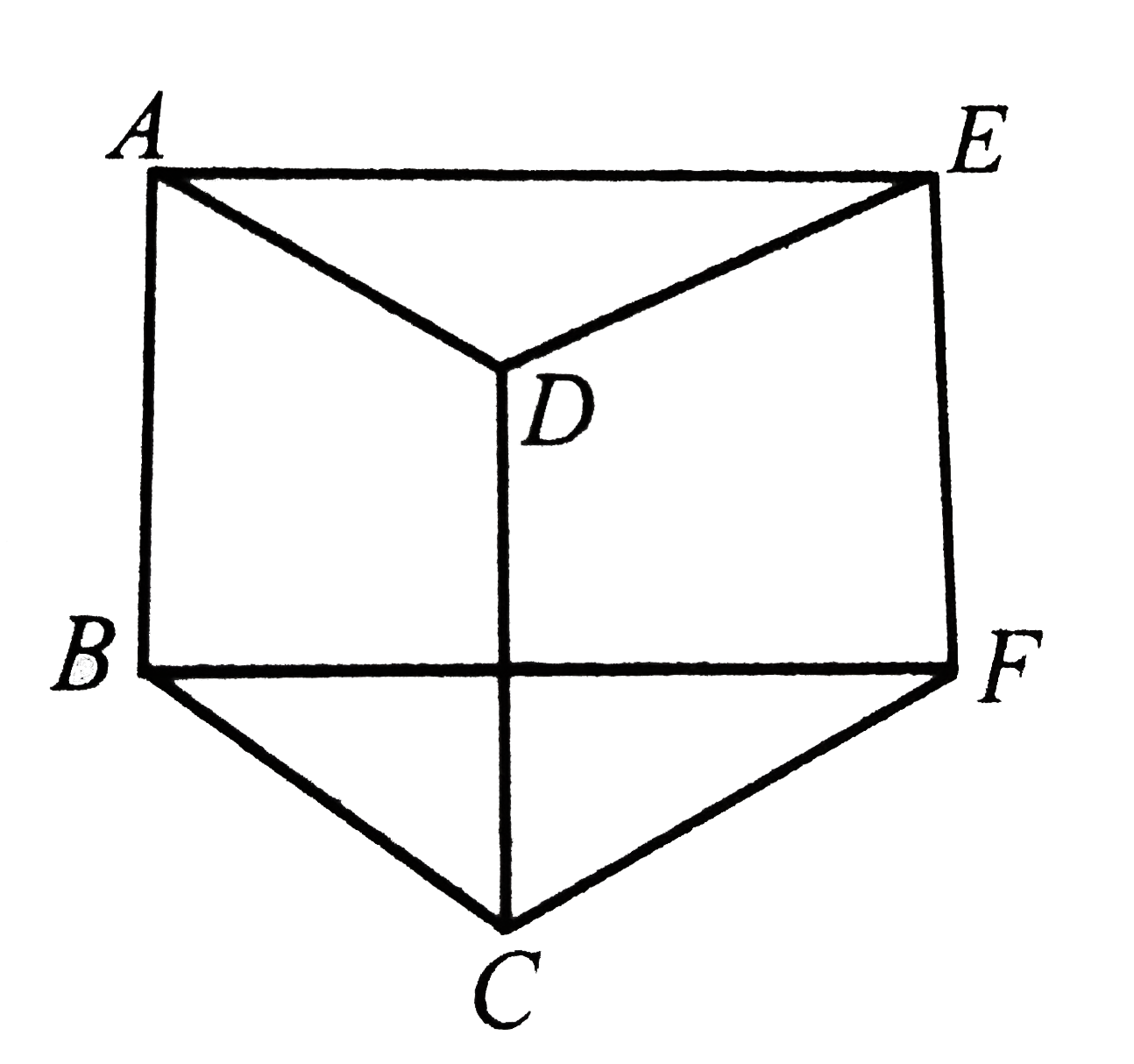
Find the equivalent resistance of the triangular bipyramid between the points.

a. `A` and `C` , b. D` and `E`
View SolutionNine wires each of resistance `r = 5 Omega` are connected to make a prism as shown in fig. find the equivalent resistance of the arrangement across AB (in `Omega`)
View SolutionThe figure shows part of certain circuit, find,
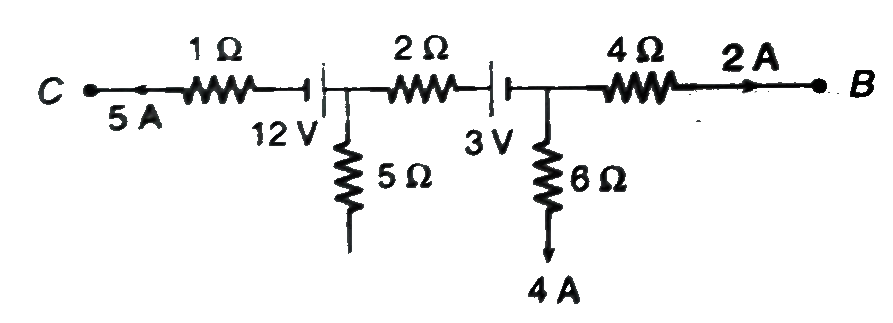
a. power dissipted in `5Omega` resistance,
b.Potential difference `V_C-V_B`
c.Which battery is being charged?
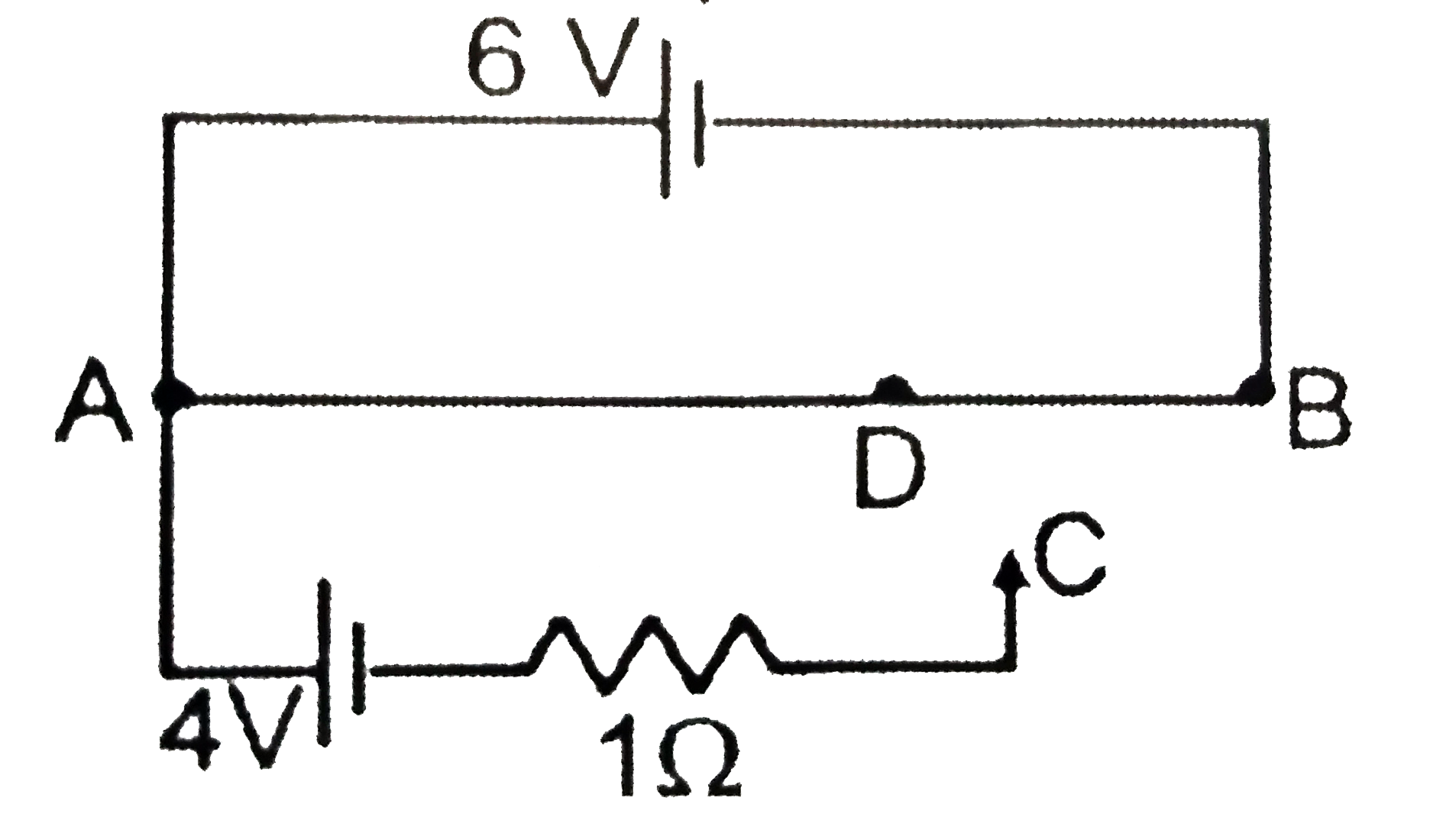
View SolutionA 6 volt battery of negligible internal resistance is connected across a uniform wire AB of length `100 cm`. The positive terminal of another battery of emf 4V and internal resistance `1 Omega` is joind to the point A as shown in figure. Take the potential at B to be zero. (a) What are the potentials at the points A and C ? (b) At which D of the wire AB, the potential is equal to the potential at C. ( c) If the point C and D are connected by a wire. What will be the current through is ? (d) Id the 4V batteryt is replaced by 7.5 V battery, what whould be the answers of parts (a) and (b) ?
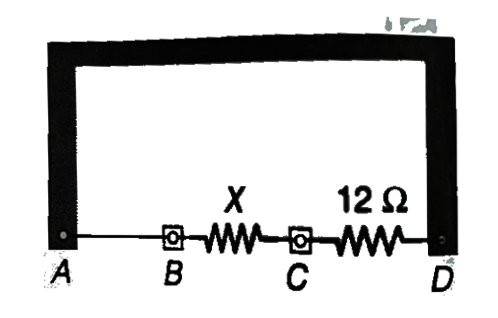
View SolutionA thin uniform wire `AB` of length `1 m`, an unknown resistance `X` and a resistance of `12 Omega` are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance `X`. Using the principle of Wheatstone bridge answer the following questions :
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey connect at appropriate points.
(c) After appropriate connections are made, it is found that no deflection takes place in th, from galvanometer when the sliding jockey touches the wire at a distance of `60 cm` from `A`. Obtain value of the resistance X.
View SolutionA galvanometer (coil resistance `99 Omega`.) is converted into an ammeter using a shunt of `1 Omega` and connected as shown in figure (a). The ammeter reads `3 A`. The same galvanometer is convened into a voltmeter by connecting a resistance of `101 Omega` in series. This voltmeter is connected at, shown in figure (b). Its reading is found to be `4/5` of the full scale reading. Find :
(a) internal resistance r of the cell
(b) range of the ammeter and voltmeter
(c) full scale deflection current of the galvanometer.

View SolutionIn a circuit shown in figure if the internal resistances of the sources are negligible then at what value of resistance `R` will the thermal power generated in it will be the maximum. What is the value of maximum power?
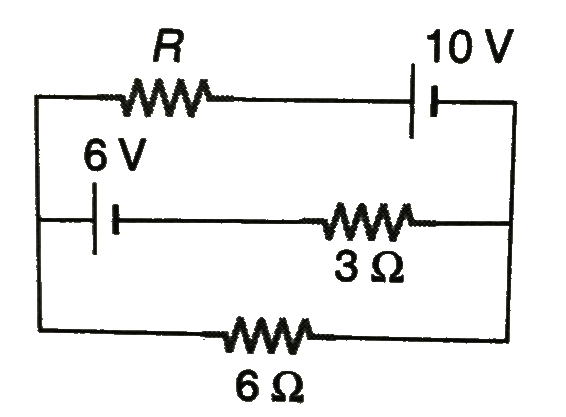
View SolutionIn the circuit shown in figure find:

a. the current in the `3.00 Omega` resistor,b. the unknown emfs`E_1` and `E_2` and c the resistance `R`.
View SolutionIn the circuit shown all the ammeters are ideal.
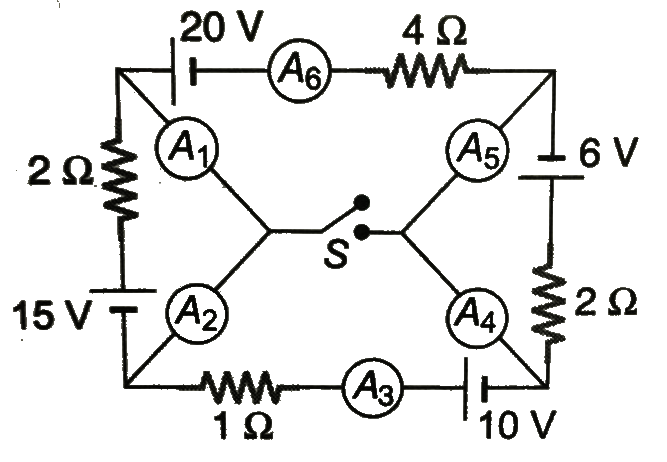
(a), If the switch S is open, find the reading of all ammeters and the potential difference across the switch.
(b) If the switch `S` is closed, find the current through all ammeters and the switch also.
View SolutionAn accumulator of emf `2 V` and negligible internal resistance is connected across a uniform wire of length 10 m and resistance `30 Omega` The appropriate terminals of a cell of emf `1.5 V` and internal resistance `1 Omega` is connected to one end of the wire and the other terminal of the cell is connected through a sensitive galvanometer to a slider on the wire. What is the length of the wire that will be required to produce zero deflection of the galvanometer? How will the balancing length change?
(a) When a coil of resistance `5Omega` is placed in series with the accumulator.
(b) The cell of `1.5 V` is shunted with `5 Omega` resistor?
View SolutionA circuit shown in the figure has resistances `20 Omega` and `30 Omega`. At what value of resistance `R_x` will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between points `A` and `B` is supposed to be constant in this case.

View SolutionIn the circuit shown in figure, the emfs of batteries are `E_1`, and `E_2` which have internal resistances `R_1`, and `R_2`. At what value of the resistance `R` will the thermal power generated in it be the highest? What it is?
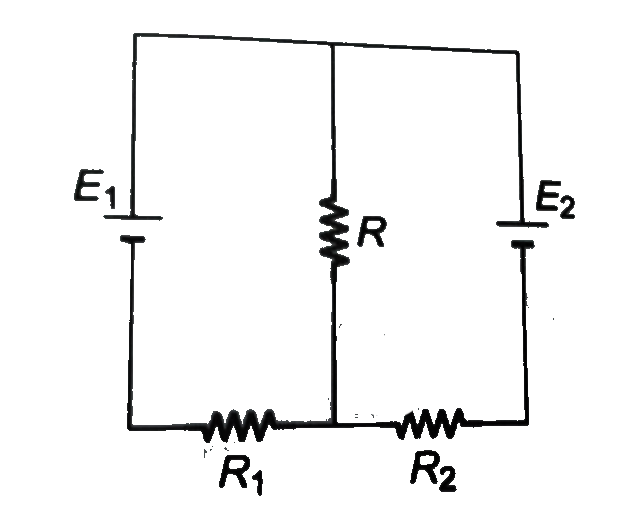
View SolutionA conductor has a temperature independent resistance `R` and a total heat capacity `C`. At the moment `t=0` it is connected to a `DC` voltage `V`. Find the times dependence of the conductors temperature t assuming the thermal power dissipated into surrounding space to vary as `q=k(T-T_0)` where `k` is a constant `T_0` is the surrounding temperature (equal to conductor's temperature at the initial moment).
View Solution
Level 2 Subjective questions and complete solutions for chapter CURRENT ELECTRICITY of DC PANDEY ENGLISH of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS CURRENT ELECTRICITY
- B. Assertion and reason
- Check point
- Example
- Example Example Type
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Exercise 23.1
- Exercise 23.10
- Exercise 23.11
- Exercise 23.12
- Exercise 23.13
- Exercise 23.2
- Exercise 23.3
- Exercise 23.4
- Exercise 23.5
- Exercise 23.6
- Exercise 23.7
- Exercise 23.8
- Exercise 23.9
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Example Type
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Medical entrances gallery
- Miscellaneous Examples
- OBJECTIVE_TYPE
- Taking it together