Complete Solutions to For JEE Advanced Only one option is correct of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| DC PANDEY MASTER PROBLEM PACKAGE | For JEE Advanced Only one option is correct |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
In Young's double slit experiment how many maximas can be obtained on a screen (including the central maximum) on both sides of the central fringe if `lambda=2000Å` and `d=7000Å`
View SolutionIn Young's double-slit experiment `d//D = 10^(-4)` (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit `I_(0)`. Then, the distance of point P from the central maximum is `(lambda = 6000 Å)`
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is `(3//2)x`. The refractive index of the second plate is
View SolutionIn Young's double-slit experiment, the y-coordinate of central maxima and 10th maxima are 2 cm and 5 cm, respectively, When the YDSE apparatus is immersed in a liquid of refractive index 1.5, the corresponding y-coordinates will be
View SolutionThe maximum intensity in Young's double slit experiment is `I_(0)` . What will be the intensity of light in front of one the slits on a screen where path difference is `(lambda)/(4)` ?
View SolutionThe coherent point sources `S_(1)` and `S_(2)` vibrating in same phase emit light of wavelength `lambda`. The separation between the sources is `2lambda`. Consider a line passing through `S_(2)` and perpendicular to the line `S_(1)S_(2)`. What is the smallest distance from `S_(2)` where a minimum of intensity occurs due to interference of waves from the two sources?
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation `d(ltltR)(d=5lambda)` symmetrically about the centre of the circle. The sources emit identical wavelength `lambda` each. What will be the number of points on the circle with constructive interference?
View SolutionIn the Young's double slit experiment apparatus shown in figure, the ratio of maximum to minimum intensity on the screen is 9. The wavelength of light used is `lambda`, then the value of y is

View SolutionIn the figure shown `S_(1)O-S_(2)O=S_(3)O-S_(2)O=(lambda)/(4)`, Intensity at O due to any one of the slits is `I_(0)`. What is the intensity due to all the three coherent sources `S_(1), S_(2) and S_(3)` ?
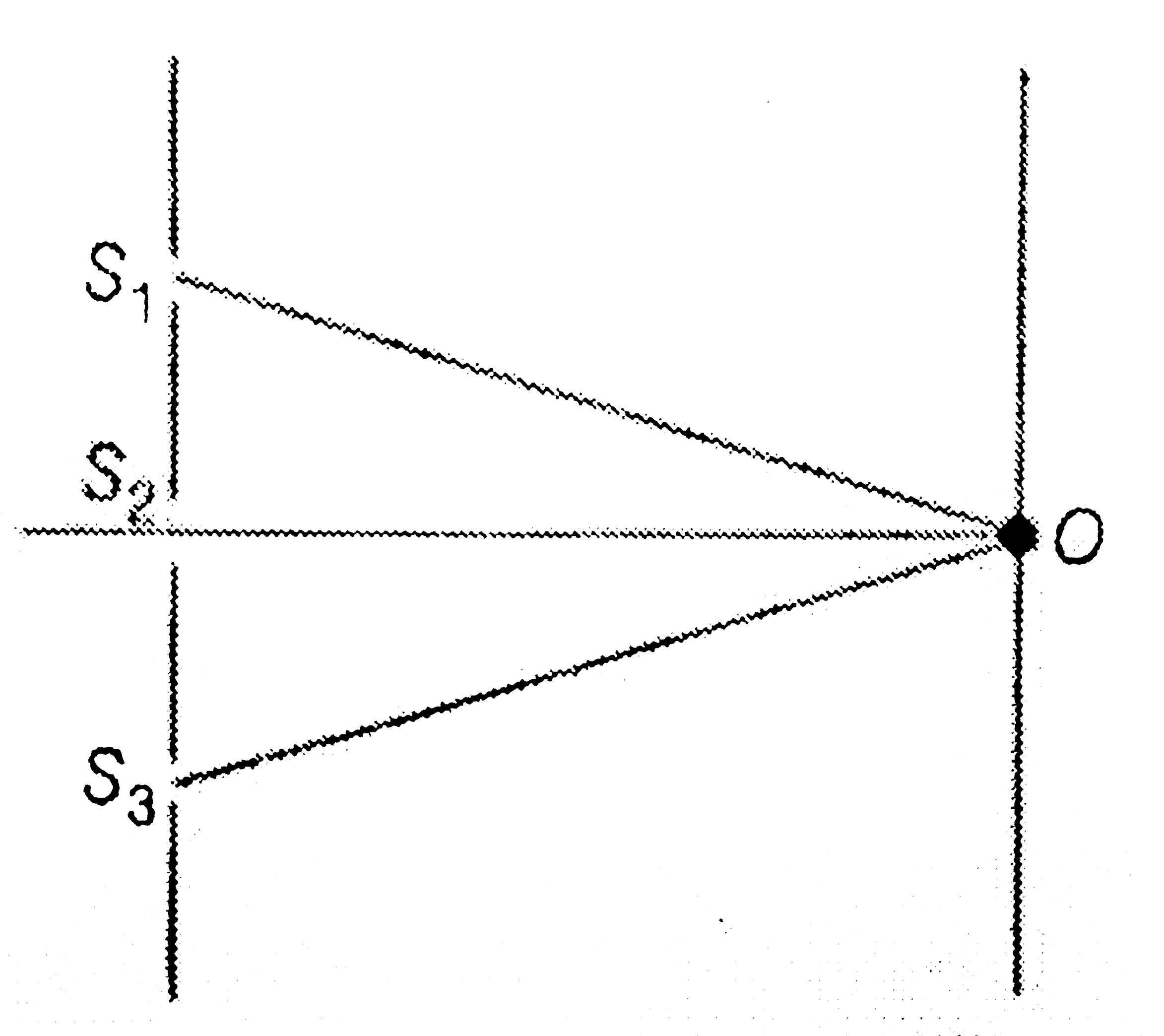
View SolutionTwo coherent light sources, each of wavelength `lambda`, are separated by a distance `3 lambda`, The maximum number of minima formed on line AB, which funs from `-oo` to `+oo`, is

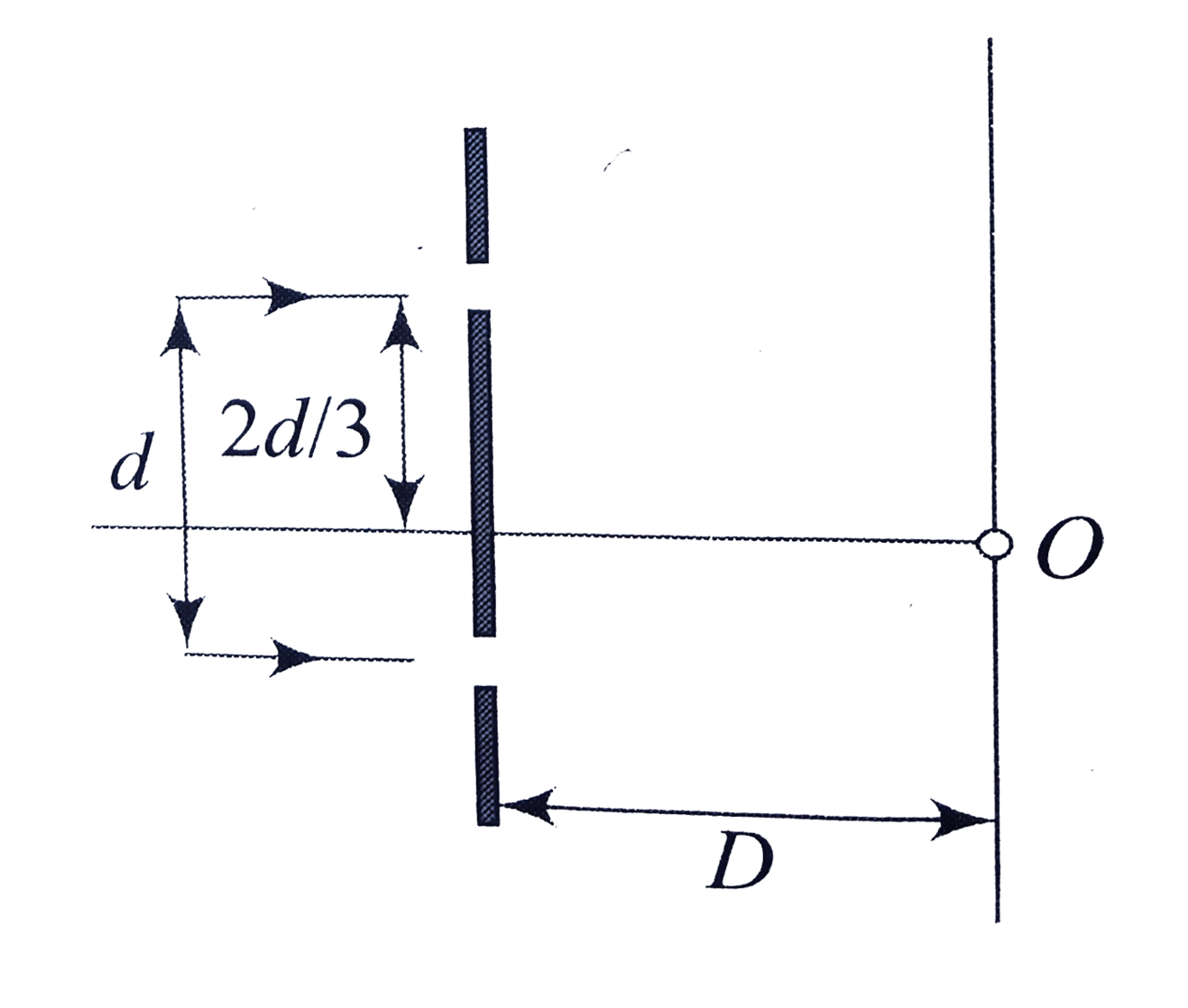
View SolutionIn figure, if a parallel beam of white light is incident on the plane of the slit, then the distance of the nearest white spot on the screen form O is [assume `d lt lt D, lambda lt lt D`]
View SolutionIn YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with `mu` will be best represented by `(mu is greater than or equal to 1)
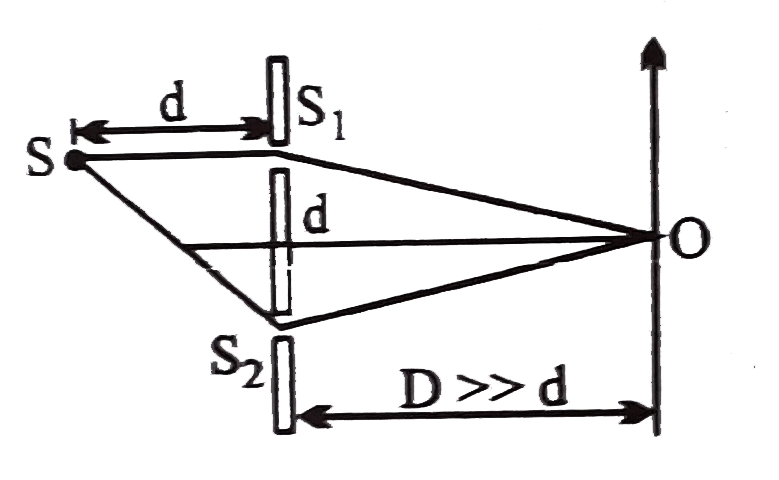
View SolutionTwo identical narrow slits `S_(1)` and `S_(2)` are illuminated by light of wavelength `lambda` from a point source P. If, as shown in the diagram above the light is then allowed to fall on a scree, and if n is a positive integer, the condition for destructive interference at Q is that

View SolutionTo make the central fringe at the center`O` , mica sheet of refractive index `1.5` is introduced Choose the corect statement.
View SolutionA thin oil film of refractive index 1.2 floats on the surface of water `(mu = 4/3)`. When a light of wavelength `lambda = 9.6xx 10^(-7)m` falls normally on the film from air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is:
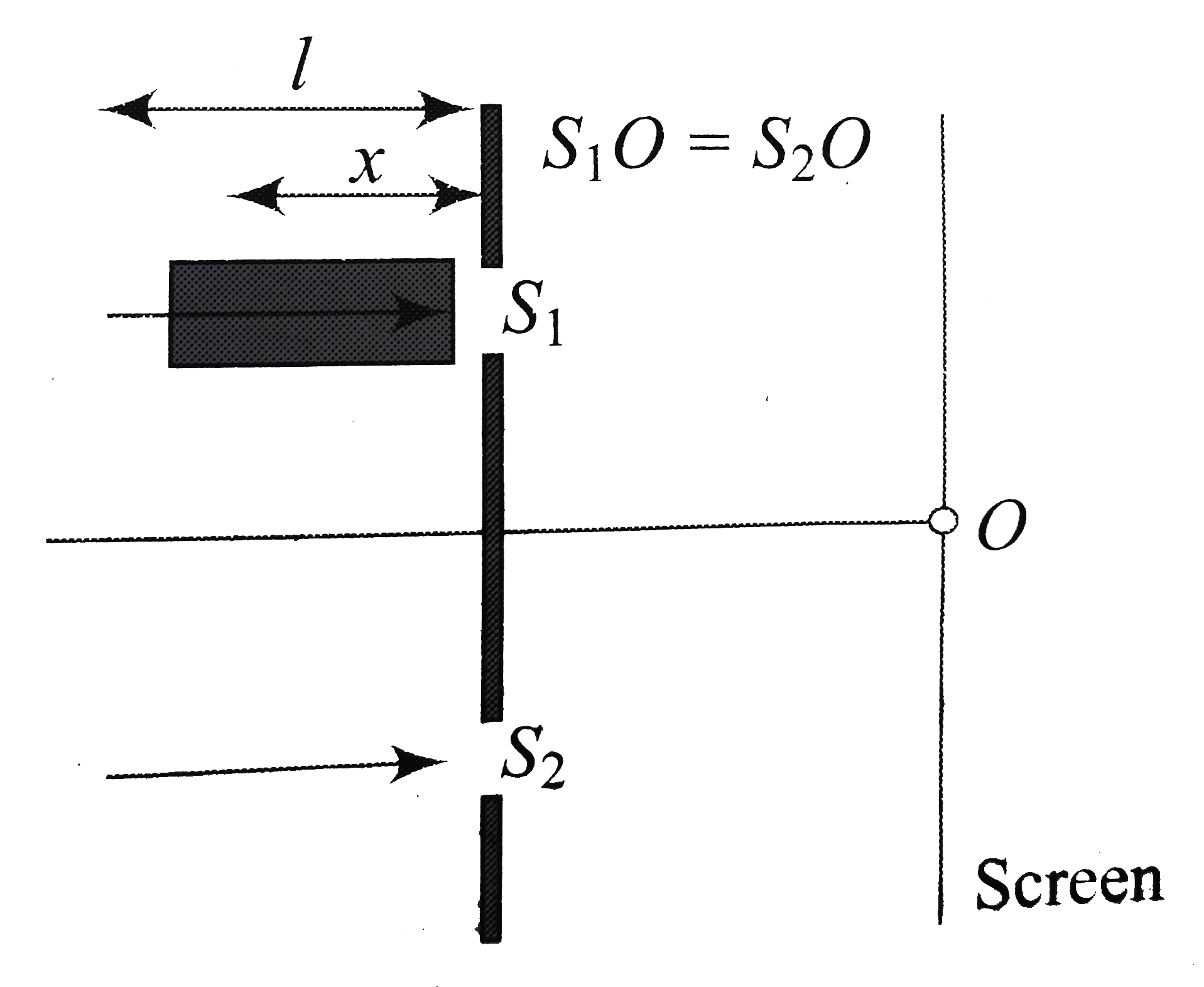
View SolutionIn figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit `S_(1)` passes through a medium of variable refractive index `mu = 1 + ax` (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on `S_(1)`. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength `lambda` in air) is
View SolutionConsider two coherent, monochromatic (wavelength `lambda`) sources `S_(1) and S_(2)`, separated by a distance d. The ratio of intensities of `S_(1)` and that of `S_(2)` (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from `S_(1)` is (if the resultant intensity at point P is equal to `(9)/(4)` times of intensity of `S_(1)`) `("Given : "angleS_(2)S_(1)P=90^(@), d gt0 and n" is a positive integer")`
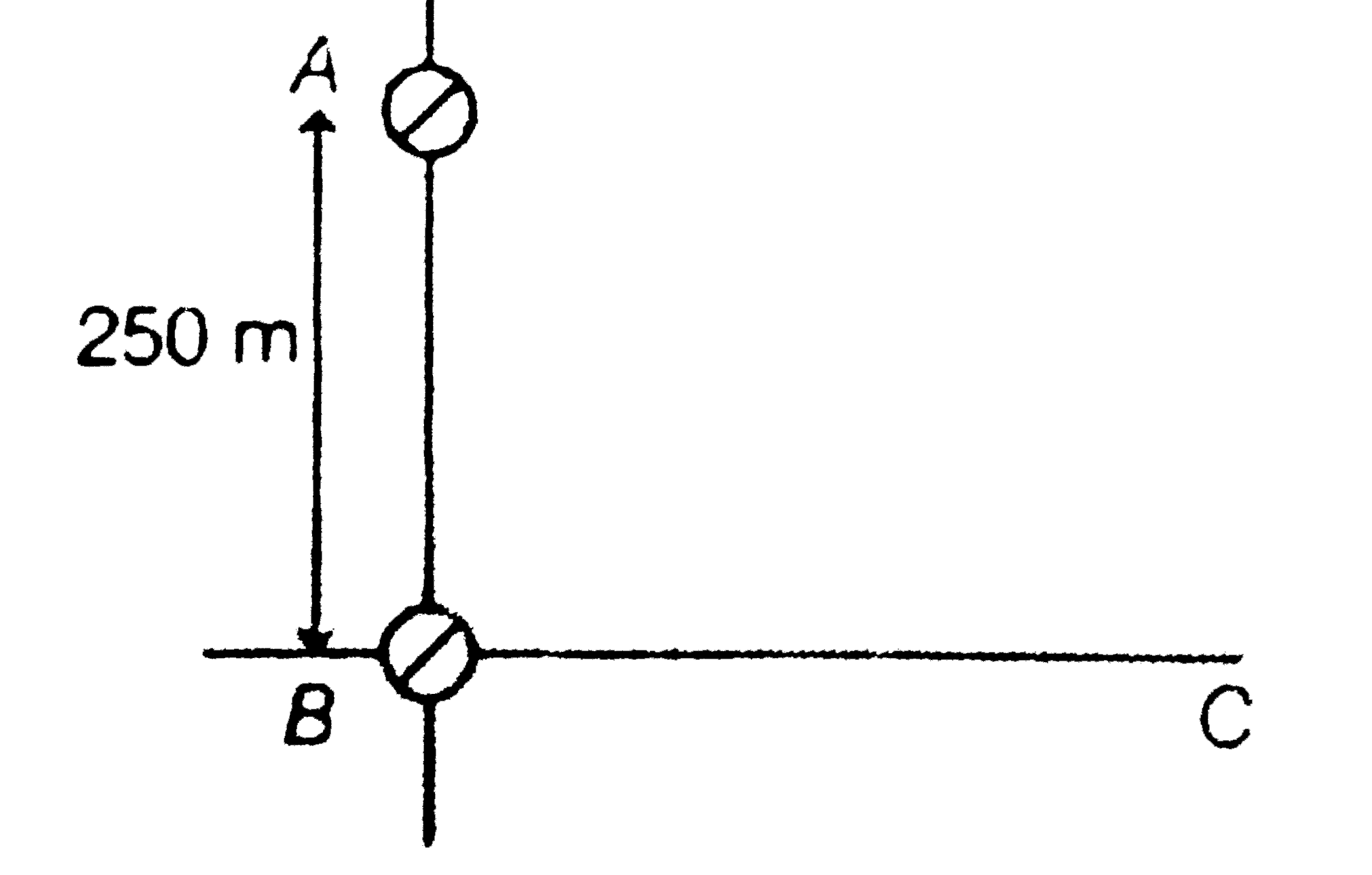
View SolutionTwo radio transmitters radiating in phase are located at point A and B, 250 m apart. The ratio wave have frequency of 3MHz. A radio receiver is moved out from point B along a line BC (perpendicular to AB). The distance from B beyond which the detector does not detect any minima si :
View SolutionA parallel beam of light of all wavelength greater than 3000Å falls on a double slit in a Young's double slit experiment. It is observed that the wavelength 3600Å and 6000Å are absent at a distance of 31.5 mm from the position of the centre maximum and the orders of the interference at this point for the two wavelength differ by 7. If the distance between the slit and the screen in 1m, the separation between the two slits is
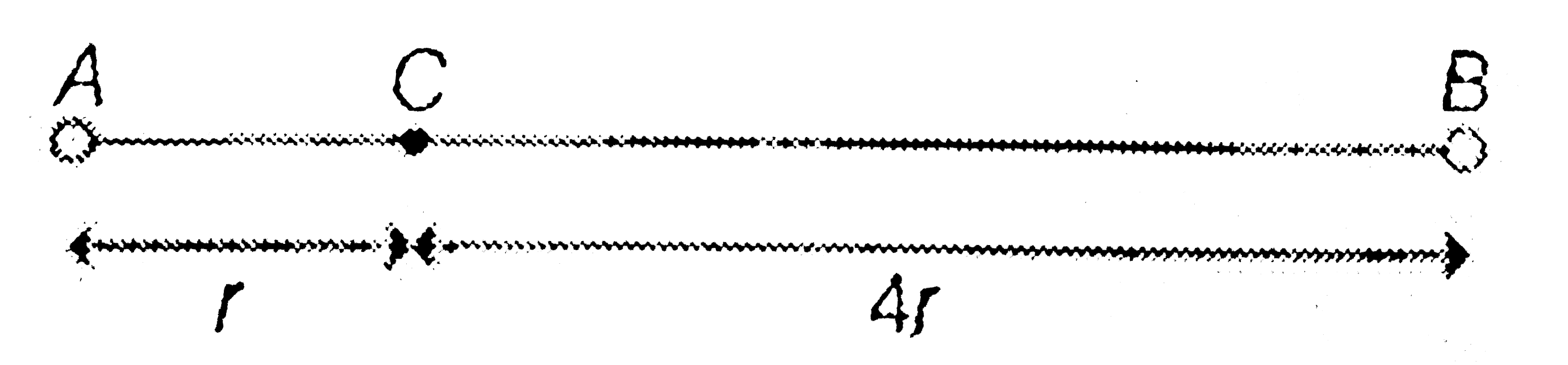
View SolutionTwo point coherent sources of power `P_(0) and 4P_(0)` emitting sound of frequency 150 Hz are kept at point A and B respectively. Both sources are in same phase. A detector is kept at point C as shown in figure. The distance of point A and B is r and 4r form detectro respectively. The speed of sound in medium is 300 m/s . Given `P_(0)=64pi` Watt and r=1m. The intensity observed by detector is
View SolutionConsider the YDSE (Young's double slit experiment ) arrangement shown in figure . The screen in the arrangement starts accelerating from rest in positive x-direction, with acceleration a=kt, (here k is a constant ), then rate of change of fringe width ( R) varies with time t as

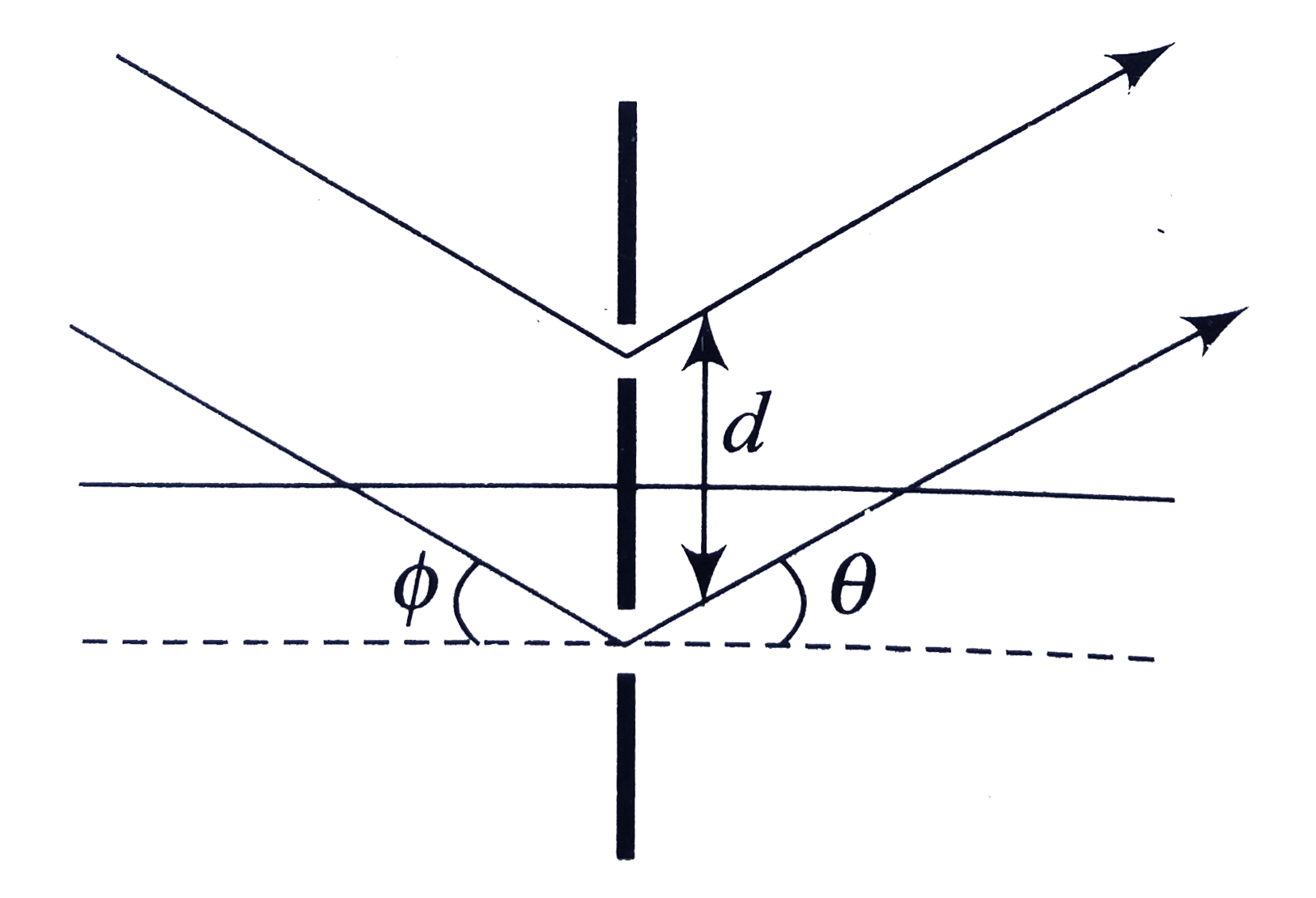
View SolutionLight is incident at an angle `phi` with the normal to a plane containing two slits of separation d. Select the expression that correctly describes the positions of the interference maxima in terms of the incoming angle `phi` and outgoing angle `theta`.
View Solution
For JEE Advanced Only one option is correct questions and complete solutions for chapter WAVE OPTICS of DC PANDEY ENGLISH of Class 12
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 12 PHYSICS WAVE OPTICS
- Assertion reason
- Check point
- Example
- For JEE Advanced B. More than one option is correct
- For JEE Advanced C. Comprehension Type Questions. Passage (I)
- For JEE Advanced C. Comprehension Type Questions. Passage (II)
- For JEE Advanced C. Comprehension Type Questions. Passage (III)
- For JEE Advanced D. Matrix Matching type Questions.
- For JEE Advanced E. Integer Type Questions
- For JEE Advanced Only one option is correct
- For JEE main (Only one option is Correct )
- match column
- medical entrances
- taking it together