Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=5λ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
20
22
24
26
The correct Answer is:A
To solve the problem of finding the number of points on a circle with constructive interference from two coherent sources, we can follow these steps:
1. Understanding the Setup:
- We have two coherent sources S1 and S2 separated by a distance d=5λ, where λ is the wavelength of the emitted waves. The sources are placed symmetrically about the center of a circle of radius R.
2. Path Difference for Constructive Interference:
- For constructive interference, the path difference Δx between the waves from the two sources at any point on the circle must satisfy the condition:
Δx=nλ
where n is an integer (0, 1, 2, ...).
3. Calculating Path Differences:
- The maximum path difference occurs when the angle subtended by the line connecting the two sources at the point on the circle is at its maximum. The maximum path difference can be calculated as:
Δxmax=d=5λ
4. Finding Possible Values of n:
- The possible values of n for constructive interference can be determined by the equation:
nλ≤5λ
- This gives us:
n≤5
- Therefore, n can take the values 0,1,2,3,4,5 which gives us a total of 6 values.
5. Counting the Points on the Circle:
- For each value of n, there are two points on the circle where constructive interference occurs (one on each side of the line connecting the two sources).
- Thus, for each n from 0 to 5, we have:
Total Points=2×(number of n values)=2×6=12
6. Conclusion:
- The total number of points on the circle where constructive interference occurs is 12.
Final Answer:
The number of points on the circle with constructive interference is 12.
- We have two coherent sources S1 and S2 separated by a distance d=5λ, where λ is the wavelength of the emitted waves. The sources are placed symmetrically about the center of a circle of radius R.
- For constructive interference, the path difference Δx between the waves from the two sources at any point on the circle must satisfy the condition:
Δx=nλ
where n is an integer (0, 1, 2, ...).
- The maximum path difference occurs when the angle subtended by the line connecting the two sources at the point on the circle is at its maximum. The maximum path difference can be calculated as:
Δxmax=d=5λ
- The possible values of n for constructive interference can be determined by the equation:
nλ≤5λ
- This gives us:
n≤5
- Therefore, n can take the values 0,1,2,3,4,5 which gives us a total of 6 values.
- For each value of n, there are two points on the circle where constructive interference occurs (one on each side of the line connecting the two sources).
- Thus, for each n from 0 to 5, we have:
Total Points=2×(number of n values)=2×6=12
- The total number of points on the circle where constructive interference occurs is 12.
The number of points on the circle with constructive interference is 12.
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced B. More than one option is correct
4 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced C. Comprehension Type Questions. Passage (I)
2 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View SolutionTwo sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo coherent fight sources A and B with separation 2λ are placed on the x-axis symme-trically about the origion. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and with centre at the origion.
View SolutionFour point charges each +q is placed on the circumference of a circle of diameter 2d in such a way that they form a square. The potential at the centre is
View SolutionA charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. The ratio of electric potentials at the centre in the two situations is
View SolutionFrom the figure, identify :(a) the centre of circle (b) three radii(b) a diameter (d) a chord(e) two points in the interior (f) a point in the exterior
View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
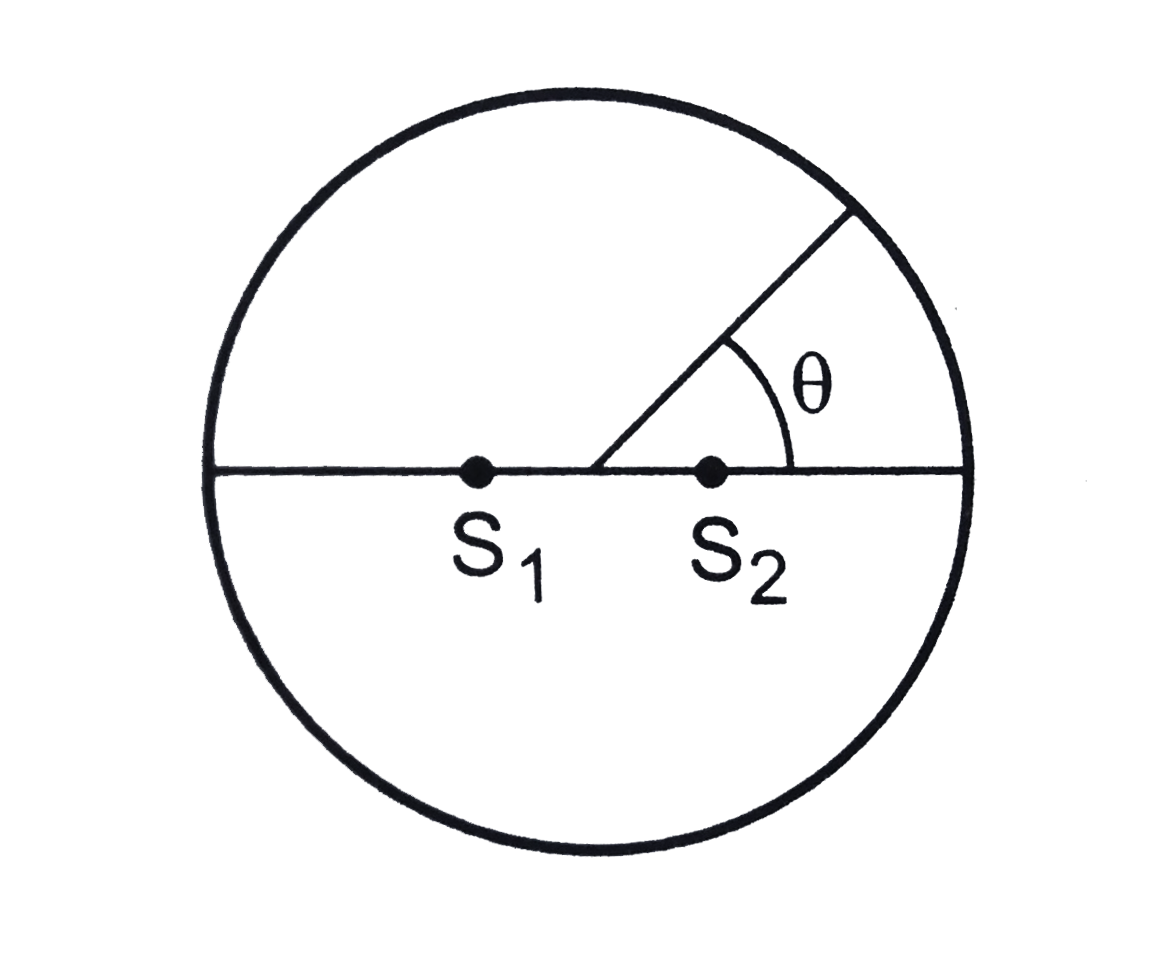
View SolutionFigure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View Solution
