Complete Solutions to जड़त्व आघूर्ण of chapter घूर्णी गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | घूर्णी गति |
| ERRORLESS HINDI | जड़त्व आघूर्ण |
| Number Of Questions | 84 |
| Academic Year | 2023-24 |
2 किग्रा द्रव्यमान के 5 कण 0.1 मीटर त्रिज्या एवं नगण्य द्रव्यमान की एक वृत्तीय चकती की परिधि से जुड़े हैं। इसके तल के लम्बवत् एवं केन्द्र से होकर गुजरने वाली अक्ष के परितः इस निकाय का जड़त्व आघूर्ण है
View Solutionसमान धातु से बनी एवं समान मोटाई की दो वलयों की त्रिज्यायें 0.2 मीटर एवं 0.6 मीटर हैं। इनके जड़त्व आघूर्णों का अनुपात होगा
View Solutionएक ठोस बेलन जिसका द्रव्यमान M, त्रिज्या R तथा लम्बाई । है। उस अक्ष के परितः जडत्व आघूर्ण क्या होगा जो इसके केन्द्र से होकर जाता है एवं स्वयं के अक्ष के लम्बवत है।
View Solutionएक व्यास के अनुदिश वलय का जड़त्व आघूर्ण है ।
View Solution10kg द्रव्यमान एवं 0.5m त्रिज्या वाले गोले का एक स्पर्श रेखा के सापेक्ष जड़त्व आघूर्ण है
View Solutionएक अर्द्धवृत्तीय वलय का उसके केन्द्र से होकर जाने वाले तथा उसके तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionसमान द्रव्यमान M एवं समान लम्बाई `l` की चार पतली छड़ें चित्रानुसार एक वर्ग बनाती हैं। इस निकाय का, केन्द्र O से गुजरने वाली एवं इसके तल के लम्बवत अक्ष के परितः जड़त्व आघूर्ण है
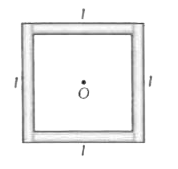
View Solutionलोहे एवं एल्यूमीनियम का उपयोग करके एक वृत्तीय चकती इस प्रकार बनायी जाती है कि इसका जड़त्व आघूर्ण इसकी ज्यामितीय अक्ष के परितः अधिकतम हो, तो इसके लिए
View Solutionकिसी एकसमान वृत्तीय चकती का इसके व्यास के परितः जड़त्व आघूर्ण I है। इसके तल के लम्बवत एवं इसकी परिधि के एक बिन्दु से होकर गुजरने वाली अक्ष के परितः इसका जड़त्व आघूर्ण होगा
View Solutionजड़त्व आघूर्ण निर्भर करता है
View Solutionकिसी वस्तु का जड़त्व आघूर्ण किस पर निर्भर नहीं करता
View Solutionएक पतली छड़ जिसका द्रव्यमान M तथा लम्बाई `l` है। इस छड़ का किसी एक सिरे से लम्बाई के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण होगा
View Solution10 किग्रा द्रव्यमान के एक पहिये का इसकी अक्ष के परितः जड़त्व आघूर्ण 160 किग्रा `”मी”^(2)` है। इसकी घूर्णन त्रिज्या होगी।
View Solutionघूर्णन गति में द्रव्यमान के तुल्य राशि है
View Solutionचार कणों को जिनमें प्रत्येक का द्रव्यमान m है, एक `l` भुजा वाले वर्ग ABCD के शीर्षों पर रखा गया है। वर्ग में A से गुजरने वाली एवं BD के समान्तर अक्ष के परितः निकाय का जड़त्व आघूर्ण होगा
View SolutionR त्रिज्या की एक चकती से । त्रिज्या का समकेन्द्रीय वृत्तीय भाग निकाल लेने पर एक वलयाकार चकती बच जाती है जिसका द्रव्यमान Mहै। बची हुई वलयाकार चकती का जड़त्व आघूर्ण उसके तल के लम्बवत एवं उसके गुरुत्व केन्द्र से गुजरने वाले अक्ष के परितः होगा
View Solutionएक समरूप तार में से दो वृतीय लूप बनाए जाते है (i) Pr त्रिज्या का एवं (ii) Q,nr त्रिज्या का। यदि Q का जड़त्व आघूर्ण, इसके तल के लम्बवत एंव केन्द्र से गुजरने वाली अक्ष के परितः P के समान अक्ष के परितः, जड़त्व आघूर्ण से 8 गुना हो तो n का मान है, (r तथा nr की तुलना में तार का व्यास नगण्य है)
View Solutionएक पतली वृत्ताकार चकती का द्रव्यमान 2kg एवं व्यास 0.2m है। चकती का जड़त्व आघूर्ण, इसके तल के लम्बवत् एवं किनारे से गुजरने वाली अक्ष के परितः होगा `(kg - m^(2)` में)
View Solutionद्रव्यमान M तथा त्रिज्या r वाले एक एकसमान वलय का जड़त्व आघूर्ण उसके तल में स्थित एक स्पर्श रेखा के परितः होता है
View SolutionM द्रव्यमान एवं R त्रिज्या वाले गोले का, इसके केन्द्र से गुजरने वाले अक्ष के परितः, जड़त्व आधूर्ण `2/5MR^(2)` है। उपरोक्त अक्ष के समान्तर एवं गोले को स्पर्श करने वाली अक्ष के परितः गोले की घूर्णन त्रिज्या है
View Solutionचार कणों को, जिनमें प्रत्येक का द्रव्यमान m है, एक । भुजा वाले वर्ग के शीर्षों पर रखा गया है। वर्ग के तल के लम्बवत एवं इसके केन्द्र से गुजरने वाली अक्ष के परितः निकाय की घूर्णन त्रिज्या है
View Solutionपिण्ड की घूर्णन त्रिज्या निर्भर करती है
View Solutionएक ठोस गोला एवं एक ठोस बेलन, जिनकी त्रिज्याएँ एवं घनत्व समान हैं, अपनी-अपनी अक्षों के परितः घूर्णन कर रहे हैं। जड़त्व आघूर्ण अधिक होगा (L = R)
View Solutionएक वृत्ताकार वलय एवं वृत्ताकार चकती दोनों के द्रव्यमान एवं त्रिज्यायें समान हैं। इनके तलों के लम्बवत् एवं केन्द्रों से गुजरने वाले अक्षों के परितः जड़त्व आघूर्णों का अनुपात है
View SolutionM ग्राम द्रव्यमान एवं 2.5cm त्रिज्या वाली चकती की, इसके तल के लम्बवत एवं गुरुत्व केन्द्र से गुजरने वाली अक्ष के परितः घूर्णन त्रिज्या है
View SolutionM द्रव्यमान एवं र त्रिज्या के तीन वलयों को दर्शाये गये चित्रानुसार व्यवस्थित किया गया है। निकाय का जड़त्व आघूर्ण YY' अक्ष के सापेक्ष होगा

View Solutionभुजा 'a' तथा द्रव्यमान 'm' की किसी एकसमान वर्गाकार प्लेट पर विचार कीजिए। इस प्लेट का उस अक्ष के परितः जो इसके तल के लम्बवत् है तथा इसके किसी एक कोने से गुजरती है, जड़त्व आघूर्ण है
View Solutionएक चकती का इसकी अक्ष के पारितः जड़त्व आघूर्ण `l` है। इसके तल में स्थित स्पर्श रेखा के परितः इसका जड़त्व आघूर्ण होगा
View Solutionवलय का द्रव्यमान m = 3 ग्राम, त्रिज्या r = 1 सेमी है। मुख्य अक्ष के समान्तर तथा वलय के तल के लम्बवत् स्पर्श रेखा के परितः इस वलय का जड़त्व आघूर्ण होगा
View Solution500 ग्राम द्रव्यमान तथा 10 सेमी त्रिज्या के बेलन का इसकी मुख्य अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionएक ठोस बेलन का द्रव्यमान M लम्बाई L तथा त्रिज्या R है। इस बेलन का जड़त्व-आघूर्ण उसके किसी जनित्र के परितः क्या है।
View Solutionएक चकती का द्रव्यमान M व त्रिज्या r है। चकती के किनारे को स्पर्श करती हुई तथा उसके तल में स्थित अक्ष के परितः अथवा व्यास के समान्तर अक्ष के परितः उसका जड़त्व आघूर्ण है
View Solutionपतली वृत्ताकार चकती का इसके व्यास के परितः जड़त्व आपूर्ण होगा (M चकती का द्रव्यमान तथा R त्रिज्या है)
View Solutionकिसी दृढ़ छड़ की लम्बाई L है और उसका द्रव्यमान नगण्य है। इसके दो विपरीत सिरों पर क्रमश: m, तथा m द्रव्यमान के दो बिन्दु पिंड रखे गये हैं। इस छड़ को उसके स्वयं के लम्बवत् अक्ष के परितः घूर्णन कराना है, जो छड़ पर स्थित किसी बिन्दु P से होकर गुजरती है (आरेख देखिये)। तो बिन्दु P की वह स्थिति जिसके लिये छड़ को कोणीय वेग `omega_(0)` से घूर्णन कराने के लिये आवश्यक कार्य न्यूनतम होगा, कौन सी है
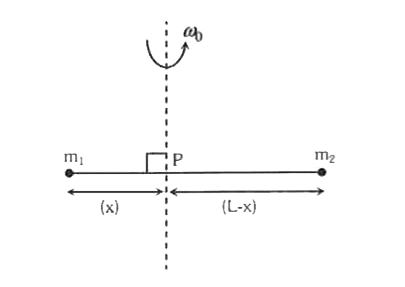
View Solutionकिसी ठोस गोले का द्रव्यमान M तथा इसकी त्रिज्या R है। इसमें से अधिकतम सम्भव आयतन का एक क्यूब (धन) काट लिया जाता है। इस क्यूब का जड़त्व आघूर्ण कितना होगा, यदि इसका घूर्णन अक्ष इसके केन्द्र से होकर गुजरता है तथा इसके किसी एक फलक के लम्बवत् है।
View Solutionखोखले गोले का द्रव्यमान M तथा त्रिज्या R है। इसके व्यास के परितः जड़त्व आघूर्ण होगा
View Solutionतीन सर्वसम गोलीय कोशों (खोखले गोले) में प्रत्येक का द्रव्यमान m तथा त्रिज्या r है। इन्हे आरेख में दर्शाया गया है। XX' एक अक्ष है, जो दो गोलीय कोशों को स्पर्श करता है और तीसरे के व्यास से होकर गुजरता है। तो Xx' अक्ष के परितः इन तीन गोलीय कोशों के निकाय का जडत्व आघूर्ण होगा।
View Solutionएक वृत्ताकार चकती का द्रव्यमान M एवं त्रिज्या R है। चकती के व्यासतः स्पर्श करने वाले तथा उसके लम्बवत् अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionसमान त्रिज्या तथा समान द्रव्यमान वाली वृत्ताकार चकती तथा वृत्ताकार वलय की घूर्णन त्रिज्याओं का अनुपात इनकी अक्ष के सापेक्ष होगा
View Solutionलम्बाई L तथा द्रव्यमान M की एक छड़ को अर्द्धवृत्तीय रूप में मोड़ा जाता है (चित्रानुसार) | XY के परितः जड़त्व आघूर्ण है

View Solutionकिसी पतली एकसमान छड़ का द्रव्यमान M और लम्बाई L हैं। उसके मध्यबिन्दु से होकर जाने वाली और उसकी लम्बाई के लम्बवत् अक्ष के परितः छड़ का जड़त्व आघूर्ण `I_(0)` है। तो, छड़ के एक सिरे से गुजरने वाली और उसकी लम्बाई के लम्बवत् अक्ष के परितः उसका जड़त्व आघूर्ण होगा
View Solutionपतली एक समान वृत्तीय चकती की विघूर्णन त्रिज्या इसके तल में स्थित तथा केन्द्र से गुजरने वाले अक्ष के परितः है
View Solution1kg द्रव्यमान तथा 2m त्रिज्या की वृत्तीय चकती के तल के लम्बवत्, द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण `2kgm^(2)` है। चकती के सतह से गुजरने वाले अक्ष के समानान्तर जड़त्व आघूर्ण होगा (दिये गये चित्रानुसार)
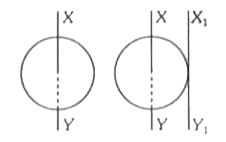
View Solutionएक समरुप छड़ का जड़त्व आघूर्ण एक सिरे से लम्बवत् गुजरने वाले अक्ष के सापेक्ष `I _(1)` है। इस छड़ को मोड़कर वलय बनाई जाती है, जिसका व्यास के परितः जड़त्व आघूर्ण `l_(2)` है। `(I_(1))/(I_(2))` का मान है
View Solutionसमबाहु त्रिभुज के तीनों शीर्षों पर m द्रव्यमान के तीन कण रखे गये हैं। त्रिभुज की भुजा की लम्बाई `a` है। इस निकाय का त्रिभुज की किसी भी भुजा के परितः जड़त्व आघूर्ण होगा :
View Solutionएक ठोस बेलन जिसका द्रव्यमान M तथा त्रिज्या R है, की वर्तुलाकार त्रिज्या बेलन के अक्ष के परितः होगी
View Solutionएक चकती की त्रिज्या R तथा द्रव्यमान 9M है, इससे द्रव्यमान M तथा त्रिज्या `R/3` की एक छोटी संकेन्द्रीय चकती पृथक कर दी जाती है शेष चकती का इसके केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण है
View Solutionकिसी एक समान वृत्ताकार डिस्क (चकती) का जड़त्व आघूर्ण अधिकतम होगा, यदि घूर्णन अक्ष डिस्क के लम्बवत् हो और उससे गुजरता हो
View Solutionएकसमान पतली छड़ की लम्बाई L तथा संहति M है। इसका उस अक्ष के परितः जड़त्व आघूर्ण, जो कि इसके एक सिरे से L/3 दूरी पर स्थित बिन्दु से होकर लम्बवत् जाती है, का मान होगा
View Solutionएक टेनिस रैकेट जो कि M द्रव्यमान तथा R त्रिज्या की एक रिंग और L लंबाई तथा M द्रव्यमान की एक छड़ से मिलकर बना है। यदि रिंग और छड़ समाक्षीय है और छड़ की रेखा रिंग के केन्द्र से गुजरती है। तब समतल के लंबवत् और रिंग के केन्द्र से अक्ष के सापेक्ष रैकेट का जड़त्व आघूर्ण होगा
View Solutionएक समान लंबाई `1/2L` तथा `m_(omega)` द्रव्यमान की लकड़ी और एक समान लंबाई `1/2L` तथा `m_(b)` द्रव्यमान की पीतल से संघटित होकर L लंबाई की एक छड़ बनाई जाती है। छड़ के लंबवत तथा इसके केन्द्र से गुजरने वाले अक्ष के सापेक्ष छड़ का जड़त्व आघूर्ण `I` होगा
View SolutionX एवं Y समान तार से बने दो लूप है। X एवं Y की त्रिज्या क्रमशः `r_(1)`तथा `r_(2)` व उनके जड़त्व आघूर्ण `I_(1)` एवं `I_(2)` है। यदि `(I_(2))/(I _(1)) = 4` हो, तो `(r _(2))/(r _(1))` का मान है
View SolutionR त्रिज्या की एक चकती का इसके व्यास के सापेक्ष जड़त्व आघूर्ण `25 kg-m^(2)` है। चकती के केन्द्र से R/2 दूरी पर व्यास के समांतर अक्ष के सापेक्ष चकती का जड़त्व आघूर्ण होगा
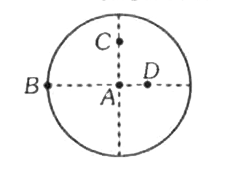
View Solutionएक वर्ग पटल ABCD दर्शाया गया है, जिसका केन्द्र 0 है, इसमें होगा
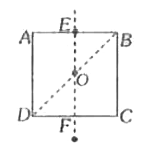
View Solutionद्रव्यमान M तथा त्रिज्या r के खोखले बेलन का स्वयं के अक्ष के परितः जड़त्व आघूर्ण है
View Solutionएक समरूप बेलन की त्रिज्या R तथा लम्बाई L है। इस बेलन का इसके वृत्तीय तल के लम्बवत् केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण एक अन्य समान बेलन की लम्बाई के लम्बवत् तथा केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण के बराबर है,
View Solutionआयत ABCD का जड़त्व आघूर्ण किस अक्ष के परितः न्यूनतम होगा (BC = 2AB)
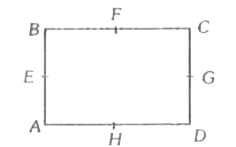
View Solutionवृत्तीय छल्ले के तल के लंबवत इसके केंद्र से होकर जाने वाली अक्ष के सापेक्ष इसका जड़त्व आघूर्ण `"200 ग्राम सेमी"^(2)` है । इसके व्यास के परितः जड़त्व आघूर्ण कितना होगा ?
View Solutionएक रेडियन प्रति सेकण्ड के कोणीय वेग से घूर्णित एक पिण्ड का किसी अक्ष के परितः जड़त्व आघूर्ण आंकिक रूप से बराबर है
View Solution2m त्रिज्या तथा 1kg द्रव्यमान की वृत्तीय चकती का इसके द्रव्यमान केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण `2 kg-m^(2)` है। इसी अक्ष के समान्तर तथा चकती के सिरे से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण `kg-m^(2)` में होगा
View Solution1 kg द्रव्यमान की वृत्तीय वलय का इसके केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण `4 kg-m^(2)` है। वलय का व्यास होगा
View Solutionद्रव्यमान M तथा त्रिज्या R की वृत्तीय वलय से `90^(@)` चाप के संगत भाग को अलग किया जाता है। शेष वलय का जड़त्व आघूर्ण उसके तल के लम्बवत् तथा केन्द्र से गुजरने वाले अक्ष के परितः `MR^(2)` का k गुना है। तब k का मान है।
View Solutionएक वलय का द्रव्यमान M तथा त्रिज्या R है, इसके केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण `I` है। तब, व्यास के परितः इसका जड़त्व आघूर्ण होगा
View SolutionM द्रव्यमान तथा R त्रिज्या की वृत्तीय चकती का द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण `I_(0)` है। एक अन्य समान द्रव्यमान तथा मोटाई किन्तु आधे घनत्व की वृत्तीय चकती का उसी अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionतीन कण, जिनमें से प्रत्येक का द्रव्यमान m है, I cm भुजा के समबाहु त्रिभुज के शीर्षों पर स्थित हैं (जैसा कि चित्र में प्रदर्शित है) रेखा AX के परितः जो कि AB के लम्बवत् है तथा ABC के तल में स्थित है, जड़त्व आघूर्ण का मान `”ग्राम/सेमी”^(2)` में होगा ।
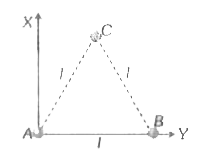
View Solutionकिसी वृत्तीय चकती के तल में स्थित स्पर्शी अक्ष के परितः घूर्णन त्रिज्या तथा उसी त्रिज्या की वृत्तीय वलय की वलय के तल में स्थित स्पर्शी अक्ष के सापेक्ष घूर्णन त्रिज्या का अनुपात होता है
View Solutionएक ठोस गोले A तथा एक अन्य खोखले गोले B के द्रव्यमान तथा बाह्य त्रिज्याएँ समान हैं। उनके व्यास के परितः जड़त्व आघूर्ण `I_(A)` तथा `I_(B)` इस प्रकार हैं कि
View Solutionबिन्दु द्रव्यमान 1, 2, 3 तथा 4kg क्रमशः बिंदुओं (0, 0,0), (2,0,0), (0,3,0) तथा (-2,-2,0) पर स्थित हैं। x अक्ष के परितः निकाय का जड़त्व आघूर्ण होगा
View Solutionबिन्दु द्रव्यमान 1, 2, 3 तथा 4kg क्रमशः बिंदुओं (0, 0,0), (2,0,0), (0,3,0) तथा (-2,-2,0) पर स्थित हैं। x अक्ष के परितः निकाय का जड़त्व आघूर्ण होगा
View Solutionएक ही पदार्थ के तथा समान आकार के एक ठोस गोले तथा खोखले गोले का भार मापे बिना उनके बीच अंतर बताया जा सकता है
View Solutionदो छड़ों को जिनमें प्रत्येक छड़ का द्रव्यमान m तथा लम्बाई । है, केन्द्र पर जोड़ कर क्रास का स्वरुप दिया जाता है। छड़ों के तल के लम्बवत् तथा उनके उभयनिष्ठ केन्द्र से होकर जाने वाली अक्ष के परितः क्रास का जड़त्व आघूर्ण होगा
View SolutionR त्रिज्या तथा 9M द्रव्यमान की एक वृत्तीय चकती से R/3 त्रिज्या की एक छोटी चकती काटी जाती है। चकती के तल के लम्बवत् तथा O से गुजरने वाली अक्ष के परितः शेष चकती का जड़त्व आघूर्ण होगा
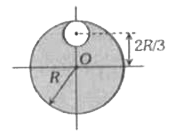
View Solutionएक ठोस गोले का द्रव्यमान M एवं त्रिज्या R है उसके द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण | है। इसे । मोटाई की एक चकती के रूप में बदल दिया जाये जिसका तल के लम्बवत एवं किनारे से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण। ही रहता है, तब चकती की त्रिज्या होगी
View Solutionद्रव्यमान M तथा त्रिज्या की किसी डिस्क से R व्यास का कोई वृताकार छिद्र इस प्रकार काटा जाता है कि उसकी नेमि डिस्क के केन्द्र से गुजरे। डिस्क के शेष भाग का, डिस्क के लम्बवत् उसके केन्द्र से गुजरने वाले अक्ष के परित जड़त्व आघूर्ण क्या है
View Solutionएक छड़ के केन्द्र से गुजरने वाले एवं तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण `(1)/(12)ML^(2)` है (जहाँ पर M द्रव्यमान और L छड़ की लम्बाई है) छड़ को मध्य बिन्दु से इस प्रकार मोड़ते हैं कि उनके सिरों के बीच का कोण `60^(@)` हो जाये तब छड़ का उपरोक्त अक्ष के परितः जड़त्व आघूर्ण होगा
View SolutionL लम्बाई तथा 1.8 kg द्रव्यमान की समरूप छड़ को इसके दोनों सिरों पर दो मापन स्केल पर विराम में रखा गया है। बांयें सिरे से L/4 दूरी पर 2.7 kg द्रव्यमान का समरूप गुटका छड़ पर रखा जाता है। दांयें सिरे पर मापन स्केल द्वारा अनुभव किया गया बल होगा
View Solutionएक गति पालक चक्र (Fly Wheel) के परिधि (Rim) का छोटा सा भाग टूट कर गिर जाता है। जबकि यह नियत कोणीय चाल से घूर्णित है, तब इसकी घूर्णन त्रिज्या का मान होगा
View Solutionr त्रिज्या वाले ठोस गोले की एक नियत अक्ष के सापेक्ष घूर्णन त्रिज्या r है। इस अक्ष की गोले के केन्द्र से दूरी होगी
View Solutionदो समान छड़ A तथा B समान द्रव्यमान m तथा लम्बाई L की हैं, इन्हें xy तल में चित्रानुसार T आकृति में जोड़ा जाता है। इनका A से सम्पाती अक्ष के परितः जड़त्व आघूर्ण है
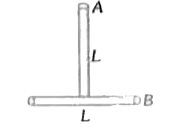
View Solutionकुछ समान द्रव्यमान के पिण्ड दिये गये हैं। उनके गुरुत्व केन्द्र से गुजरने वाले एवं पिण्ड के तल के लम्बवत अक्ष के परितः अधिकतम जड़त्व आघूर्ण किसका होगा
View Solutionएक छड की लम्बाई 2L एवं द्रव्यमान m प्रति इकाई लम्बाई है। छड़ के केन्द्र से गुजरने वाले तथा इसकी लम्बाई के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionएक हल्की छड़ की लम्बाई । है। इसके दो सिरों से क्रमश: `m_(1)` तथा `m_(2)` द्रव्यमान के पिण्ड संलग्न है। इस छड़ के लम्बवत तथा इसके द्रव्यमान केन्द्र से गुजरते हुए अक्ष के परितः इस निकाय का जड़त्व आघूर्ण होगा
View Solutionएक त्रिज्या R तथा लम्बाई । के एक समान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व आघूर्ण | है। जड़त्व आघूर्ण के निम्नतम मान के लिए अनुपात 1/R क्या होगा
View Solutionचित्रानुसार सात एक जैसी वृत्ताकार समतल डिस्कों, जिनमें प्रत्येक का द्रव्यमान M तथा त्रिज्या R है, को सममित रूप से जोड़ा जाता है। समतल के लंबवत् तथा P से गुजरने वाली अक्ष के सापेक्ष, इस संयोजन का जड़त्व आघूर्ण है
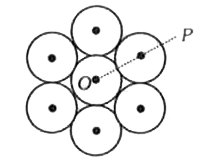
View Solution
जड़त्व आघूर्ण questions and complete solutions for chapter घूर्णी गति of ERRORLESS PHYSICS (HINDI) of Class 12