Complete Solutions to JEE SECTION of chapter घूर्णी गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | घूर्णी गति |
| ERRORLESS HINDI | JEE SECTION |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
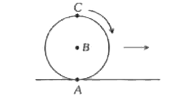
एक स्थिर क्षैतिज समतल पृष्ठ पर एक गोला बिना फिसले लुढ़क रहा है। चित्र में, A तल से सम्पर्क बिन्दु, B गोले का केन्द्र तथा C उसका सबसे ऊपरी बिन्दु है, तब
View Solutionएक घर्षणयुक्त नत समतल का झुकाव कोण `theta` है, एक ठोस बेलन नीचे की ओर लोटनिक गति कर रहा है, तब
View Solutionएक ठोस बेलन का द्रव्यमान m और त्रिज्या R है एक `theta` झुकाव के नत समतल पर लुढ़क रहा है। यदि नत समतल और बेलन के बीच घर्षण गुणांक `mu` हो, तब
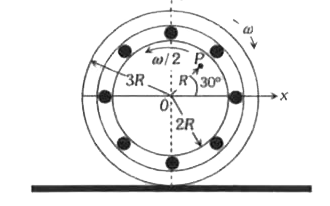
View Solutionचित्र में दिखाये निकाय के हिस्से हैं: (i) 3R बाहरी-त्रिज्या की रिंग, जो क्षैतिज सतह पर`omega` कोणीय चाल से दक्षिणावर्त बिना फिसले लुढ़क रही है, और (ii) 2R त्रिज्या की भीतरी डिस्क जो `omega//2` कोणीय चाल ये वामावर्त घूम रही है। घर्षण-रहित बॉल-बियरिंग (गोलियों) रिंग और डिस्क को एक दूसरे से अलग रखते हैं। निकाय x-Z तल में है। भीतरी डिस्क पर बिन्दु P उद्गम से R दूरी पर है और OP क्षैतिज से 30° का कोण बनाता है। तब क्षैतिज सतह के सापेक्ष
View Solutionm द्रव्यमान के एक कण की स्थिति-सदिश `vecr` नीचे समीकरण में दिया गया है
`vecr (t) =alphat ^(3) hati + beta t^(2) hatj,` जिसमें `alpha -= 10 //3ms ^(3),beta =5m s^(-2)` एवं `m =0.1 kg.` है। समय t=1s पर, निम्नलिखित में से कौन सा/कौन से कथन सत्य है/है
View Solutionएक गोलीय चकती क्षैतिज सतह पर बिना फिसले लुढ़क रही है तथा चकती का केन्द्र एक समान वेग । से गति कर रहा है चकती के शिरों के किसी बिन्दु पर वेग का मान क्या हो सकता है
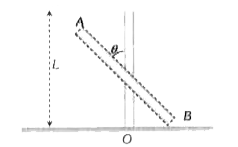
View Solutionएक L लम्बाई का दृढ़ दंड AB अपनी ऊर्ध्वाधर स्थिति से घर्षणहीन अनुभूमिक तल पर चित्रानुसार फिसल रहा है। समय के किसी क्षण पर दंड उध्याधर से बनाया कोण `theta` है। निम्न में से कौनसा (से) प्रकथन सही है/हैं
View Solutionकथन-1 : यदि किसी पिण्ड पर उसके द्रव्यमान केन्द्र के सापेक्ष कोई बाह्य बल आघूर्ण नहीं होता है। तब द्रव्यमान केन्द्र का वेग नियत रहता है।
कथन-2 : विलगित निकाय का रेखीय संवेग नियत रहता है।
View Solutionकथन-1 : समान द्रव्यमान तथा समान त्रिज्या के दो बेलन, एक खोखला (धातु) तथा दूसरा ठोस (लकड़ी) का है, इन्हें समान ऊँचाई से एक साथ छोड़ा जाये तो दोनों बिना फिसले लुढ़ककर नतसमतल के आधार तक पहुँचते हैं। दोनों में से खोखला बेलन आधार तक पहले पहुँचेगा।
कथन-2 : ऊर्जा संरक्षण के नियम से, दोनों बेलनों की कुल गतिज ऊर्जा, नत समतल की तली पर समान होती
View Solutionकथन-1 : यदि एक दृढ़ पिण्ड का जड़त्व आघूर्ण दो अक्षों के परितः बराबर है तब दोनों अक्ष समानान्तर होने चाहिए। कथन-2 : समानान्तर अक्ष प्रमेय से `I=I_(cm)+md ^(2),` जहाँ सभी पदो के सामान्य अर्थ हैं।
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समाक्ष रूप से लगाया गया है। चकती के जड़त्व आघूर्ण, उभयनिष्ठ अक्ष के परितः क्रमशः I तथा 21 है। स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2omega` प्राप्त करती है। समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है। दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है।
उपरोक्त प्रक्रम में गतिज ऊर्जा का क्षय है
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समाक्ष रूप से लगाया गया है। चकती के जड़त्व आघूर्ण, उभयनिष्ठ अक्ष के परितः क्रमशः I तथा 21 है। स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2omega` प्राप्त करती है। समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है। दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है।
जब चकती B को चकती A के सम्पर्क में किया जाता है, तब वे समय में उभयनिष्ठ कोणीय वेग प्राप्त कर लेती है। इस समय अन्तराल में एक चकती द्वारा दूसरी से प्राप्त औसत घर्षण बल आघूर्ण है
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समाक्ष रूप से लगाया गया है। चकती के जड़त्व आघूर्ण, उभयनिष्ठ अक्ष के परितः क्रमशः I तथा 21 है। स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2omega` प्राप्त करती है। समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है। दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है।
अनुपात `x_(1)//x_(2)` है
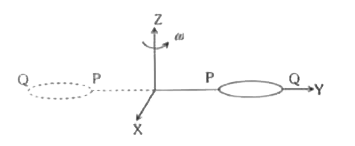
View Solutionव्यापक रूप से किसी दृढ़ पिण्ड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते है: (i) उसके संहति–केन्द्र की किसी अक्ष के परितः गति, और (ii) उसके संहति-केन्द्र से गुजरने वाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति। यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों। उदाहरण के लिए हम क्षैतिज तल में रखी एक समान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये)। यह डिस्क-छड़ निकाय उद्गम के परितः `omega` कोणीय चाल से घर्षण रहित क्षैतिज तल में घूम रहा है। तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं (i) डिस्क के संहति केन्द्र का 2-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने संहति केन्द्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक अक्ष पर घूर्णन (जो कि बिन्दुओं P और Q के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल`omega` है।
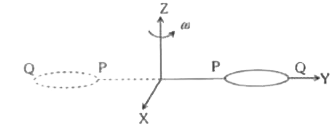
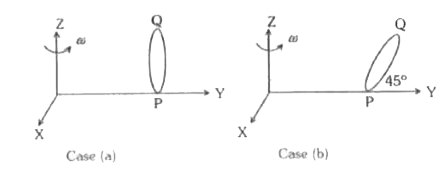
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें। Case(a): डिस्क का पृष्ठ ऊर्ध्वाधर है और x-z तल के समांतर है, Case(b): डिस्क का पृष्ठ x - y तल में `45^(@)` कोण बनाता है एवं उसका क्षैतिज व्यास x- अक्ष के समांतर है। दोनों cases में डिस्क बिन्दु P पर जड़ित है तथा यह निकाय zअक्ष के परितः `omega` कोणीय चाल से घूर्णन करता हैं
तात्क्षणिक-अक्ष (जो संहति-केन्द्र से गुजर रहा है) के परितः घूर्णन की कोणीय चाल के बारे में कौन सा प्रकथन सही है
View Solutionव्यापक रूप से किसी दृढ़ पिण्ड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते है: (i) उसके संहति–केन्द्र की किसी अक्ष के परितः गति, और (ii) उसके संहति-केन्द्र से गुजरने वाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति। यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों। उदाहरण के लिए हम क्षैतिज तल में रखी एक समान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये)। यह डिस्क-छड़ निकाय उद्गम के परितः `omega` कोणीय चाल से घर्षण रहित क्षैतिज तल में घूम रहा है। तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं (i) डिस्क के संहति केन्द्र का 2-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने संहति केन्द्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक अक्ष पर घूर्णन (जो कि बिन्दुओं P और Q के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल`omega` है।
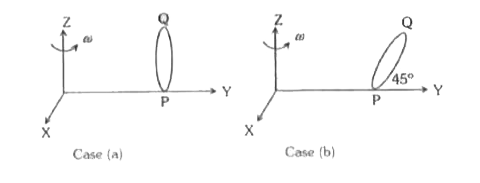
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें। Case(a): डिस्क का पृष्ठ ऊर्ध्वाधर है और x-z तल के समांतर है, Case(b): डिस्क का पृष्ठ x - y तल में `45^(@)` कोण बनाता है एवं उसका क्षैतिज व्यास x- अक्ष के समांतर है। दोनों cases में डिस्क बिन्दु P पर जड़ित है तथा यह निकाय zअक्ष के परितः `omega` कोणीय चाल से घूर्णन करता हैं
तात्क्षणिक-अक्ष (जो संहति-केन्द्र से गुजर रहा है) के बारे में कौन सा प्रकथन सही है
View Solutionएक अवितान्य डोरी से जुडा हुआ M द्रव्यमान का एक कण स्थिर बिन्दु 0 के परितः R त्रिज्या के ऊर्ध्वाधर वृत्त में गति कर रहा हैं। यह चित्रानुसार निम्नतम स्थिति पर क्षैतिज दिशा में वेग `u`आरोपित करता हैं। निम्न जानकारी दी गई हैं (i)
h ऊँचाई पर वेग सूत्र `v^(2) =u^(2) -2gh` के प्रयोग से ज्ञात किया जा सकता है
(ii) कण वृत्त को पूर्ण करेगा यदि `u ge sqrt (5gR)`
(iii) कण निचले अर्धभाग `(0^(@) lt theta lt 90^(@))` में दोलन करेगा यदि `0 lt u le sqrt (2gR)`
(iv) ‘h’ ऊँचाई पर तनाव का परिमाण सूत्र `T= (M)/(R) {u^(2) + gR - 3gh)` के प्रयोग से ज्ञात किया जाता है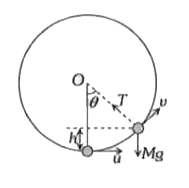
यदि R=2m, M=2kg तथा u=12m/s तब निम्नतम स्थिति पर तनाव का मान है
View Solutionएक अवितान्य डोरी से जुडा हुआ M द्रव्यमान का एक कण स्थिर बिन्दु O के परितः R त्रिज्या के ऊर्ध्वाधर वृत्त में गति कर रहा हैं। यह चित्रानुसार निम्नतम स्थिति पर क्षैतिज दिशा में वेगv आरोपित करता हैं। निम्न जानकारी दी गई हैं (i)
h ऊँचाई पर वेग सूत्र `v^(2) =u^(2) -2gh` के प्रयोग से ज्ञात किया जा सकता है
(ii) कण वृत्त को पूर्ण करेगा यदि `u ge sqrt (5gR)`
(iii) कण निचले अर्धभाग `(0^(@) lt theta lt 90^(@))` में दोलन करेगा यदि `0 lt u le sqrt (2gR)`
(iv) ‘h’ ऊँचाई पर तनाव का परिमाण सूत्र `T= (M)/(R) {u^(2) + gR - 3gh)` के प्रयोग से ज्ञात किया जाता है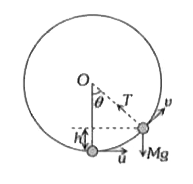
ऊपर दिए गए प्रश्न में, यदि R=2m, M=2kg तथा u=12m/s तब प्रक्षेप्य पथ के उच्चतम् बिन्दु पर तनाव होगा
View Solutionएक अवितान्य डोरी से जुडा हुआ M द्रव्यमान का एक कण स्थिर बिन्दु 0 के परितः R त्रिज्या के ऊर्ध्वाधर वृत्त में गति कर रहा हैं। यह चित्रानुसार निम्नतम स्थिति पर क्षैतिज दिशा में वेग`u` आरोपित करता हैं। निम्न जानकारी दी गई हैं (i)
h ऊँचाई पर वेग सूत्र `u^(2) =u^(2) -2gh` के प्रयोग से ज्ञात किया जा सकता है
(ii) कण वृत्त को पूर्ण करेगा यदि `mu ge sqrt (5gR)`
(iii) कण निचले अर्धभाग `(0^(@) lt theta lt 90^(@))` में दोलन करेगा यदि `0 lt u le sqrt (2gR)`
(iv) ‘h’ ऊँचाई पर तनाव का परिमाण सूत्र `T= (M)/(R) {u^(2) + gR - 3gh)` के प्रयोग से ज्ञात किया जाता है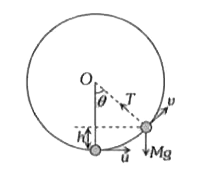
यदि M=2kg, R=2m तथा u=10m/s कण का वेग जब `theta= 60^(@)`
View Solutionएक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग `omega` से घूमती हुई डिस्क पर बद्ध निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है। गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल `F_(rot)` तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल `vecF_(l n)` को महसूस करता है। `vecF_(rot)` और `vecF_(l n)` के बीच का संबंध निम्नलिखित समीकरण में दिया गया है `vecF _(rot) = vecF_(i n) + 2m (vecv _(r ot) xx vecomega)+ m (vec omega xx vecr) xx vecomega.`
यहाँ पर `vec v _(rot)` घूमते हुए निर्देश तंत्र में कण का वेग है तथा । कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश है।
माना कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर काणीय गति `omega` से अपने अक्ष पर वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिंदु डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है, z-अक्ष खाँचे के अभिलम्ब पर है एवं -अक्ष घूमने वाली अक्ष के समानान्तर है `(vec omega = omega hatk) lm` द्रव्यमान वाले एक छोटे गुटके को समय `t=0` पर `vecr = (R//2)hat i` बिन्दु पर धीरे से इस तरह रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
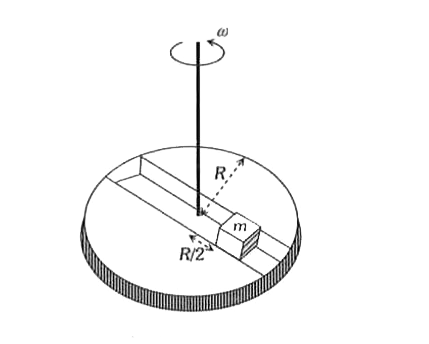
समय । पर गुटके की दूरी का मान है
View Solutionएक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग `omega` से घूमती हुई डिस्क पर बद्ध (fixed) निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है। गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल `vecF_("rot")` तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल `vecF_m` को महसूस करता है। `vecF_("rot")` और `vecF_m` में के बीच का सम्बन्ध निम्नलिखित समीकरण में दिया गया है
`vecF_("rot") = vecF_m + 2m (vecV_("rot") xx vecomega) + m(vecomega xx vecr) xx vecomega`
यहाँ पर `vecV_("rot")` घूमते हुए निर्देश तंत्र में कण का वेग है तथा `vecr` कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश (position vector) है। माना कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर कोणीय गति `omega` से अपने अक्ष पर वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिन्दु डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है, y-अक्ष खाँचे के अभिलम्ब पर है एवं z-अक्ष घूमने वाली अक्ष के समानान्तर है `(vecomega = omega hatk)`| m द्रव्यमान वाले एक छोटे गुटके को समय `t = 0` पर `vecr = (R//2)hati` बिन्दु पर धीरे से इस तरह से रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
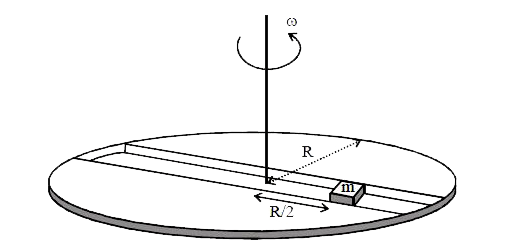
गुटके पर डिस्क की नेट प्रतिक्रिया (net reaction) है :
View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग `omega_(0)` से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक `mu` एवं गुरूत्वीय त्वरण g है

वलय की कुल गतिज ऊर्जा
View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग `omega_(0)` से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक `mu` एवं गुरूत्वीय त्वरण g है
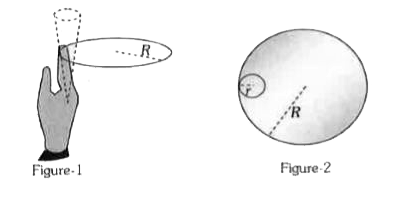
न्यूनतम `omega _(0 )` जिसके कम होते ही वलय गिर जायेगा वह है
View Solution`sqrt5cm` व्यास के चार ठोस गोलों, प्रत्येक का द्रव्यमान `0.5kg` है, को एक 4cm भुजा के वर्ग के कोनों पर क्रमशः रखा गया है। वर्ग के कर्ण पर इस निकाय का जड़त्व आघूर्ण यदि `N xx 10 ^(-4) kg - m ^(2)` हो, तब N का मान है
View Solutionएक लड़का छड़ी से एक रिंग को 2 N बल लगाकर धकेल रहा है (चित्र देखिये)। रिंग का द्रव्यमान 2 kg और त्रिज्या 0.5 m है। रिंग बिना फिसले `0.3m//s ^(2)` के त्वरण से लुढ़क रहा है। रिंग और जमीन के बीच घर्षण गुणांक इतना है कि लुढ़कना हमेशा संभव है। यदि छड़ी और रिंग के बीच घर्षण (P/10) हो, तब P का मान है

View Solutionएक एकसमान द्रव्य घनत्व की 2R त्रिज्या की गोल डिस्क में से एक 2R व्यास की छोटी गोल डिस्क निकालकर एक पटल (lamina) बनाया गया है (चित्र देखिए)। इस पटल का जड़त्व आघुर्ण 0 और P से जानेवाले अक्षों के परितः क्रमशः `I_(O)` एवं `I_(P)` हैं। दोनों अक्ष पटल तल के लम्बवत् हैं। तब अनुपात `(I_(P))/(I_(O))` निकटतम पूर्णांक में क्या है
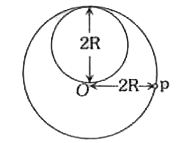
View Solution30 cm त्रिज्या के एक खोखले गोले को एक खुरदुरे नतसमतल पर विरामावस्था से छोड़ा जाता है। कोई भी फिसलन रोकने के लिए घर्षण पर्याप्त हैं। गोले का कोणीय वेग (rad/s में) ज्ञात कीजिए जब यह 3 cm की ऊर्ध्वाधर ऊँचाई से नीचे की ओर आता हैं
View Solutionएक 50 kg व 0.4m त्रिज्या की एकसमान डिस्क अपनी ऊर्ध्वाधर अक्ष के गिर्द `10 rad //s^(-1)` के कोणीय वेग से घूम रही है। दो एकसमान वृत्ताकार छल्ले धीरे से डिस्क पर सममित तरीके से एक दूसरे को छूते हुए इस प्रकार डिस्क तल पर रखे जाते है कि वे डिस्क के अक्ष को भी स्पर्श करें। प्रत्येक छल्ले का द्रव्यमान 6.25 kg व त्रिज्या 0.2 m है। इस निकाय का नया कोणीय वेग `(rads ^(-1)` में) निम्न होगा (मान लीजिए कि डिस्क एवम् छल्ले के बीच घर्षण इतना है कि डिस्क व छल्ले के बीच सापेक्ष गति शून्य है और निकाय मूल अक्ष पर घूर्णन कर रहा है)
View Solutionचित्र में दिखाया गया 0.5m त्रिज्या तथा 0.45 kg द्रव्यमान वाला एक क्षैतिज वृत्तीय प्लेटफार्म अपने अक्ष के परितः घूमने के लिए स्वतंत्र है। दो द्रव्यमान रहित कमानी वाली खिलौना बन्दूके (toy-guns), जिन पर 0.05 kg द्रव्यमान वाली स्टील की गेंद लगी है, प्लेटफार्म के व्यास पर केन्द्र से 0.25 m की दूरी पर, केन्द्र के दोनों ओर स्थित हैं। दोनों बन्दूके एक साथ गोलियों के व्यास के लंबवत् क्षैतिज तल में विपरीत दिशा में दागती है। प्लेटफार्म को छोड़ने के पश्चात् गोलियों की भूमि के सापेक्ष क्षैतिज दिशा में गति `9 ms^(-1)` है। गोलियों के प्लेटफार्म छोड़ने के पश्चात् प्लेटफार्म की घूर्णीय गति `rad ^(-1)` में है
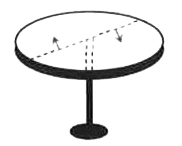
View Solutionएक एकसमान वृत्ताकार डिस्क जिसका द्रव्यमान 1.5 kg तथा त्रिज्या 0.5m है, प्रारम्भ में घर्षण रहित क्षैतिज सतह पर विरामावस्था में है। बराबर परिमाण F=0.5N वाले तीन बल एक साथ t=0 चित्र में दिखाये गये समबाहु त्रिभुज XYZ, जिसके शीर्ष बिंदु डिस्क की परिधि पर स्थित है, की भुजाओं के अनुदिश लगाये जाते हैं। बलों को लगाने के 1 सैकण्ड पश्चात् डिस्क की कोणीय गति `rad s^(-1)` में है
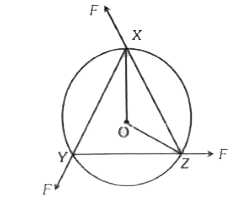
View SolutionR त्रिज्या के दो ठोस गोलों A और B के घनत्वों का त्रिज्य दूरी के साथ संबंध क्रमशः `rho _(A) (r ) = k ((r)/(R))` तथा `rho _(B) (r ) =k ((r)/(R)),` है, जहाँ k एक स्थिरांक है। गोलों का अपने-अपने केन्द्र से होकर जाने वाले अक्षों के परितः जड़त्वाघूर्ण क्रमशः `I_(A)` तथा `I_(B)` है। यदि `(I_(B))/(I_(A)) = (n)/(10),` है, तब n का मान है
View Solutionएक कण R त्रिज्या के वृत्त की परिधि पर चाल `u = 2t ^(2)` से गति कर रहा है। कॉलम-I में दी गई राशियों को कॉलम-II में दिए गए अनुकूल परिमाणों के साथ सुमेलित कीजिए

View Solutionएक व्यक्ति केन्द्र के समीप घूम रहे प्लेटफॉर्म पर खड़ा है। वह प्लेटफॉर्म की परिधि की ओर चलता है तथा अपनी प्रारम्भिक स्थिति पर वापस आता है, तब

View Solutionद्रव्यमान (mass) m के एक कण की स्थितिज ऊर्जा (potential energy) `V (r ) =kr ^(2) //2` है, जहाँ एक नियत बिंदु (fixed point) 0 से कण की दूरी है और उचित विमाओं (dimensions) वाला एक धनात्मक नियतांक (positive constant) है। यह कण बिंदु 0 के सापेक्ष R त्रिज्या वाली एक वृत्तीय कक्षा (circular orbit) में घूम रहा है। यदि कण की चाल है और L बिंदु के सापेक्ष इसके कोणीय संवेग (angular momentum) का परिमाण (magnitude) है, तो निम्नलिखित कथनों में से कौन सा (से) सही है (हैं)
View Solution1.0 kg द्रव्यमान (mass) की एक वस्तु समय t = 0 पर मूलबिंदु (origin) पर विरामावस्था में है। इस वस्तु पर एक बल `vecF = (alpha t hati + beta hatj)` लगाया जाता है, जहाँ `alpha = 1.0 Ns^(-1)` और `beta =1.0N` हैं। समय । = 1.0s पर मूलबिंदु के सापेक्ष वस्तु पर लगने वाला बल आघूर्ण (torque) `tau` है। निम्नलिखित कथनों में से कौन सा (से) सही है (हैं)
View Solutionएक वृत्ताकार वलय (ring) और एक वृत्ताकार चकती (disc), एक आनत तल (inclined plane) के शीर्श पर अगल-बगल (side by side) विरामावस्था में हैं। आनत तल, क्षैतिज तल (horizontal plane) से `60^(@)` का कोण बनाता है। दोनों वस्तुएं एक ही पल, न्यनतम दूरी वाले पथ पर बिना फिसले लोटना (rolling without slipping) आरम्भ करती हैं। यदि दोनों वस्तुओं के क्षैतिज तल पर पहुँचने का समयांतर `(2- sqrt3) //sqrt10 s` हो, तो आनत तल के शीर्श की ऊँचाई __ मीटर है। `g = 10 ms ^(-2)` लें।
View Solutionनीचे दी गयी सूची-1 में, एक कण के चार विभिन्न पथ, समय के विभिन्न फलनों (functions) के रूप में दिये गये हैं। इन फलनों में `alpha` और `beta` उचित विमाओं वाले धनात्मक नियतांक (positive constants) हैं, जहाँ `alpha ne beta` । प्रत्येक पथ में कण पर लगने वाला बल या तो शून्य है या संरक्षी (conservative) है। सूची-II में कण की पाँच भौतिक राशियों का विवरण दिया गया है: `vecp` रेखीय संवेग (linear momentum) है,`vecL` मूल बिंदु (origin) के सापेक्ष कोणीय संवेग (angular momentum) है,Kगतिज ऊर्जा (kinetic energy) है, U स्थितिज ऊर्जा (potential energy) है और E कुल ऊर्जा (total energy) है। सूची-1 के प्रत्येक पथ का सूची-II में दिये गये उन राशियों से सुमेल कीजिये, जो उस पथ के लिए संरक्षी (conserved) हैं।
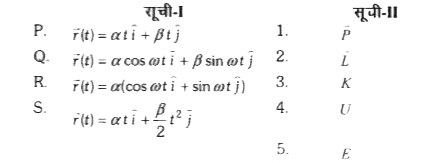
View Solution
JEE SECTION questions and complete solutions for chapter घूर्णी गति of ERRORLESS PHYSICS (HINDI) of Class 12