Complete Solutions to CRITICAL THINKING OBJECTIVE QUESTIONS of chapter घूर्णी गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | घूर्णी गति |
| ERRORLESS HINDI | CRITICAL THINKING OBJECTIVE QUESTIONS |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
प्रारम्भ में विराम स्थिति से दो कण A व B एक दूसरे की तरफ, परस्पर आकर्षण बल के कारण गति करते हैं। जब A की चाल । तथा B की चाल 20 है, उस क्षण निकाय के द्रव्यमान केन्द्र की चाल है
View Solutionएक चकती क्षैतिज सतह पर बिना फिसले लुढ़क रही है। C इसका केंद्र है तथा Q व P, C से समान दूरी पर स्थित बिन्दु हैं। यदि P, Q तथा C पर बिन्दुओं के वेग क्रमशः `u _(rho) ,u_(Q)` तथा `v _(C)` हों, तब

View SolutionR त्रिज्या एवं `R/6` मोटाई की एक वृत्तीय चकती का इसके तल के लम्बवत् तथा केन्द्र से होकर गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण । है। इसे पिघलाकर एक ठोस गोला बनाया गया है। व्यास के परितः इस गोले का जड़त्व आघूर्ण होगा
View Solutionकिसी एकसमान वृत्ताकार चकती में से, एक-चौथाई वृत्तखण्ड काटा गया है। इस वृत्त खण्ड का द्रव्यमान M है। इसको, इसके तल के लम्बवत् पूर्ण चकती के केन्द्र से गुजरने वाली रेखा के परितः घूर्णन कराते है। इसका घूर्णन अक्ष के परितः जड़त्व आघूर्ण है
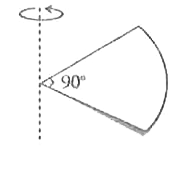
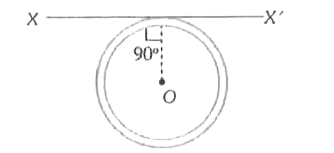
View SolutionLलम्बाई एवं एकसमान रैखिक द्रव्यमान घनत्व `rho` वाले एक पतले तार को एक वृत्ताकार लूप में (चित्रानुसार) मोड़ा जाता है, जिसका केन्द्र ० है। XX' अक्ष के परितः लूप का जड़त्व आघूर्ण है
View Solutionदो चकतियाँ, जिनकी मोटाई समान है परन्तु त्रिज्यायें अलग-अलग हैं, दो विभिन्न पदार्थों से इस प्रकार बनी हुई हैं कि इनके द्रव्यमान रागान है। पदार्थों के घनत्व 1:3 के अनुपात में है। इनके केन्द्रों से गुजरने वाले एवं तलों के लम्बवत् अक्षों के परितः चकत्तियों के जड़त्व आघूर्णों का अनुपात है
View Solutionएक समरूप वर्गाकार प्लेट का AB अक्षा के परितः जड़त्व आघूर्ण है। AB यह अक्ष है जो कि प्लेट के केन्द्र से जाती है तथा किन्हीं दो भुजाओं के समान्तर है। CD प्लेट के तल में वह रेखा है जो कि केन्द्र से होकर गुजरती है तथा AB से `theta` कोण बनाती है। CD अक्ष के परितः प्लेट का जड़त्व आघूर्ण होगा
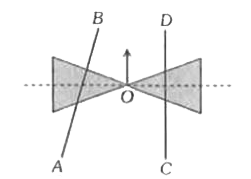
View Solutionदो शंकु को उनके शीर्ष 0 पर जोड़कर एक रोलर बनाया गया है और उसे AB व CD रेल पर असममित रखा गया है (चित्र देखिये) रोलर का अक्ष CD से लम्बवत् है और ० दोनों रेल के बीचों बीच है। हल्के से धकेलने पर रोलर रेल पर इस प्रकार लुढ़कना आरम्भ करता है कि 0 का चालन CD के समांतर है (चित्र देखिये) चालित हो जाने के बाद यह रोलर
View Solutionस्पर्शरेखीय लगाये गये बल `F=(20t-5t^(2))` न्यूटन (जहाँ । सेकण्ड में नापा गया है) के कारण 2m त्रिज्या की एक चिरनी अपने अक्ष पर घूर्णन करती है। यदि घूर्णन अक्ष के ईर्द-गिर्द घिरनी का जड़त्व आघूर्ण `10kg m^(2)` हैं, तब घिरनी की गति की दिशा प्रतिलोमित होने से पहले घिरनी द्वारा किये गये चक्करों की संख्या हैं
View Solutionकोण `theta` के नततल पर एक ठोस बेलन नीचे की ओर लोटनिक गति करता है। समतल तथा बेलन के मध्य स्थैतिक घर्षण गुणांक`mu_(s)` है। बेलन फिसले नहीं इसके लिये शर्त है
View Solutionएक कण एकसमान वृत्तीय गति कर रहा है। वृत्तीय तल के किस बिन्दु के परितः कण का कोणीय संवेग सदैव संरक्षित रहेगा
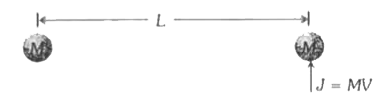
View Solutionचित्र में दिखाये गये निकाय में समान द्रव्यमान की दो एकसमान गेदें एक हल्की एवं दृढ़ छड़ के द्वारा आपस में जुड़ी हैं। यदि आवेग J = MV निकाय पर एक सिरे पर अरोपित किया जाये तो इसका कोणीय वेग क्या होगा
View SolutionM द्रव्यमान तथा । त्रिज्या की एक पतली वृत्ताकार चलय नियत कोणीय वेग `omega` से घूम रही है। चलय के व्यास के दोनों सिरों पर दो कण, प्रत्येक m द्रव्यमान का, जोड़ दिये जाते हैं। वलय का कोणीय वेग अब होगा
View SolutionLलम्बाई की छड़ का एक सिरा (x=0) मूल बिन्दु पर तथा दूसरा सिरा (x=L) पर रखा गया है। इसका द्रव्यमान प्रति इकाई लम्बाई AX है (जहाँ पर Aनियतांक है) तब इसका द्रव्यमान केन्द्र होगा
View Solutionद्रव्यमान m अचर वेग से X-अक्ष के समान्तर एक रेखा में गति कर रहा है। मूलबिन्दु अथवा Z-अक्ष के सापेक्ष इसका कोणीय संवेग ।
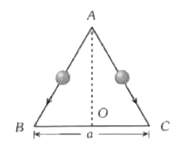
View Solutionसमान तारों से निर्मित एक समबाहु त्रिभुज पर दो सूक्ष्म मोती प्रारंभ में A पर स्थित हैं। त्रिभुज को उधिर अक्ष A0 के परितः घूर्णन कराने पर मोती एक साथ स्थिर अवस्था से छोड़े जाते हैं एवं एक मोती AB के अनुदिश तथा दूसरा AC के अनुदिश खिसकता (चित्रानुसार) है। मोती के " - नीचे की ओर खिसकने पर संरक्षित राशियाँ हैं। (घर्षण नगण्य है)
View Solutionएक पतली एक समान छड का जड़त्व आघूर्ण ।1 है जो कि इसके केन्द्र से होकर जाने वाले लम्बवत अक्ष के परितः घूम रही है। यदि इसी छड़ को मोड़कर यलय के रूप में परिवर्तित कर दिया जाये और व्यास के परित इसका जड़त्व आघूर्ण I2 हो तो `I/I`का अनुपात होगा।
View Solutionलम्बाई की एक छड़, जिसके एक सिरे पर कम द्रव्यमान m लटका हुआ है छड़ के मध्य बिन्दु के लगभग ऊर्ध्वाधर समतल में एक समान कोणीय गति `omega`से घूर्णन कर रही है। घूर्णन के दौरान, किसी समय जब छड़ क्षैतिज हो जाती है तो भार छड़ से अलग हो जाता है परंतु छड तब भी समान कोणीय गति `omega` से लगातार घूर्णन करती रहती है। भार ऊर्ध्वाधर ऊपर की ओर गति करके छड़ के उसी बिन्दु पर वापस आ जाता है। उस स्थान पर गुरुत्व के दौरान त्वरण होगा।
View Solutionएक ललका, अपनी केंद्रीय अक्ष के परितः घूर्णन कर रहे प्लेटफार्म के केन्द्र पर हाथ बांधकर खड़ा है। निकाय की गतिज ऊर्जा Kहै। बच्चा अब अपने हाथों को फैला देता है, जिससे निकाय का जड़त्व आघूर्ण दुगुना हो जाता है। निकाय की गतिज ऊर्जा हो जायेगी
View Solutionएक बेलन नततल पर लुढ़कता हुआ कुछ ऊँचाई तक पहुँचता है एवं फिर नीचे की ओर लुढ़कता है। इन गतियों के दौरान बेलन बिना फिसले लुढ़कता है) बेलन पर कार्यरत् घर्षण बल की दिशायें है
View Solutionएक 21 लंबाई की एकसमान छड़ का एक सिरा क्षैतिज तल पर है। यह क्षैतिज तल से `alpha` कोण पर झुकी है। अब यह संपर्क बिन्दु के परितः घूमकर बिना फिसले गिर रही है। क्षैतिज तल में आने पर इसका कोणीय वेग हेगा
View Solutionएक वृत्ताकार मंच एक घर्षणरहित ऊधिर पर टिका है। इस मंच की त्रिज्या R= 2m है और इसका जड़त्व आघूर्ण `200 kgm^(2)` है। प्रारम्भ में यह बिरामावस्था में है। 50kg द्रव्यमान का एक व्यक्ति इस मंच के किनारे पर खड़ा होता है और किनारे-किनारे भू-तल के सापेक्ष `1ms^(-1)` के वेग से चलना प्रारम्भ करता है तो, इस व्यक्ति द्वारा एक चक्कर पूरा करने में लगा समय होगा।
View Solutionसेमी त्रिज्या की चकती से एक 2 सेमी त्रिज्या की चकत्ती को इस प्रकार निकालते हैं कि केन्द्रों के बीच की दूरी 3.2 सेमी रहे तो चकती का द्रव्यमान केन्द्र विस्थापित होगा
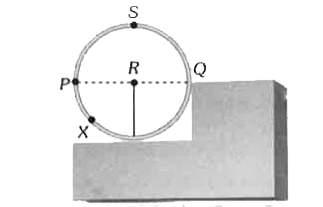
View Solutionएक त्रिज्या R एवं द्रव्यमान M का पहिया एक R ऊँचाई गाले दृढ़ सोपान के तल पर रखा है (जैसे चित्र में दिखाया गया है)। पहिये को सोपान चढ़ाने मात्र के लिए एक अचर बल पहिये के पृष्ठ पर सतत् कार्यरत है। कागज के पृष्ठ से अभिलम्ब दिशा में बिन्दु से जाने वाली अक्षा के सापेक्ष बलआघूर्ण `tau` मानिये। निम्न में से कौन(सा) से प्रकथन सही है/है
View Solutionद्रव्यमान M तथा त्रिज्या R के एक ठोस समांग बेलनाकार रोलर को एक क्रिकेट पिच पर क्षैतिज बल `F_(s)` से खींचा जा रहा है। यह मानते हुए कि बेलन बिना फिसले लुढ़कता है, इसके कोणीय त्वरण का मान होगा
View Solutionएक समतल को पोंछे से साफ करने की एक मशीन द्वारा R त्रिज्या के पोछे को कुल ऊधिर बल F से दबाकर उसे उसकी अक्ष के परितः एक नियत कोणीय गति से घुमाया जाता है। यदि बल F पोंछे पर एकसमान वितरीत है तथा पोंछे तथा समतल के बीच घर्षण गुणांक `mu` है, तो मशीन द्वारा पोंछे पर लगाया गया बल आघूर्ण होगा
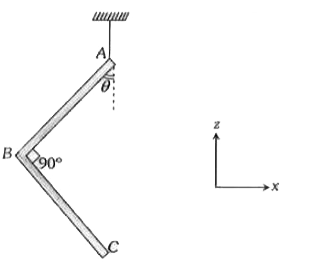
View Solutionएकसमान द्रव्यमान घनत्व की छड़ों से बनायी हुई L-आकृति के एक वस्तु को चित्रानुसार, एक डोरी से लटकाया गया है। यदि AB = BC, तथा AB द्वारा ऊर्ध्वाधर निम्न दिशा से बनाया कोण `theta है, तो
View Solution50 cm की एक छड़ के एक सिरे को कीलकित किया हैं। इसको क्षैतिज से `30^(@)` कोण पर, चित्रानुसार, उठाकर स्थिरावस्था से छोड़ दिया जाता हैं जब यह छड़ क्षैतिज अवस्था से गुजरती है तो इसकी कोणीय चाल का `rad s ^(-1)` में मान होगा: (दिया है`g= 10 ms ^(-2))`

View Solutionलम्बाई की एक पतली रोधी छड़ पर रेखीय आवेश धनत्य `=rho _(0) (x)/(l)` है। इस छड़ के मूलबिन्दु (x = 0) से जाने वाली तथा छड़ के लम्बवत् एक अक्ष के परितः । चक्कर प्रति सेकण्ड से घुमाया जाता है। इस छड़ का कालिक माध्य चुम्बकीय आघूर्ण होगा
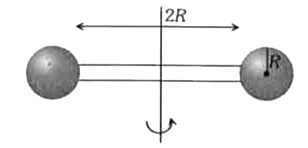
View Solutionद्रव्यमान M तथा त्रिज्या R की दो एकसमान गोलाकार गेंदों को 2R लम्बाई तथा द्रव्यमान M की एक छड़ के सिरों पर चित्रानुसार जोड़ा गया है। इस संयोजन का छड़ के केन्द्र से जाने वाली तथा छड़ के लम्बवत् अक्ष के परितः जड़त्व आपूर्ण का मान होगा
View Solutionएक द्रव्यमान रहित तथा / की छड़ पर दो द्रव्यमान चित्रानुसार उसके सिरों पर लगाये हैं। तथा उसे एक क्षैतिज अक्ष पर बिन्द । से कीलकित किया जाता है। जब इस छड़ को तिज अवस्था से छोड़ा जाता है तो उसका तात्क्षणिक कोणीय त्वरण होगा
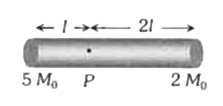
View Solutionएक पतले ठोस लकड़ी के फलक से एक त्रिभुज ABC काटा गया हैं (चित्र देखिए) दर्शाए गये अनुसार D, E तथा F इसकी भुजाओं के मध्य बिन्दु हैं तथा G त्रिभुज का केन्द्र है। G से गुजरने वाली तथा त्रिभुज के समतल के लम्बवत् अक्ष के सापेक्ष त्रिभुज का जडत्व आघूर्ण `I_(0).` है। यदि छोटा त्रिभुज DEF त्रिभुज ABC में से निकाल लिया जाये तो शेष बचे हुए भाग का उसी अक्ष के सापेक्ष जडत्व आघूर्ण है। तब
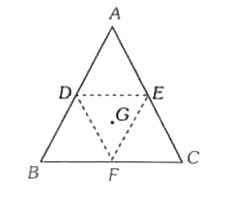
View Solutionदिखाये गये चित्रानुसार एक तख्त पर समान परिमाण F के दो बल `vecF_(1)` तथा `vecF_(2)` लगाये गये है। बल`vecF_(2)XY` समतल में है जबकि बल `F_(1)Z-` दिशा के अनुदिश बिन्दु `(vec(2i) + vec(3j))` पर लगा है। बिन्दु 0 के सापेक्ष इन बलों का आघूर्ण होगा
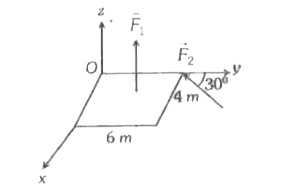
View Solution5kg द्रव्यमान तथा 0.5m. त्रिज्या के एक खोखेले बेलन पर एक डोरी को लपेटा गया है। यदि डोरी को अब 40N, के क्षैतिज बल से खींचा जाता है और, बेलन बिना फिसले क्षैतिज समतल पर लुढ़कता है (चित्र देखिये) तो, बेलन का कोणीय त्वरण होगा (डोरी का द्रव्यमान तथा मोटाई नगण्य है)

View Solution1kg द्रव्यमान पर मूल बिन्दु के सापेक्ष बल आघूर्ण का परिमाण 2.5Nm है। यदि इस पर लगने वाला बल 1N है, तथा कण की मूल बिन्दु से दूरी 5m है तो बल तथा स्थिति सदिश के बीच कोण (रेडियन में) हैं
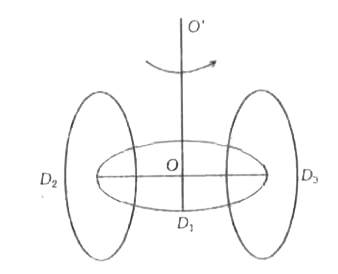
View Solutionद्रव्यमान M तथा त्रिज्या R की एक डिस्क `D_(1)` से समान द्रव्यमान M तथा त्रिज्या R की दो डिस्क `D_(2)` तथा `D _(3)`को आमने सामने दृढ़तापूर्वक जोड़ा गया है इस संयोजन का, दिखाये गये चित्रानुसार `D_(1)` के केन्द्र से गुजरने वाली अक्ष 00' के सापेक्ष, जड़त्व आघूर्ण होगा
View Solutionआंतरिक त्रिज्या 10 cm बाझा त्रिज्या 20 तथा लम्बाई 30 cm के एक खोखले बेलन का जडत्व आघूर्ण, उसकी अक्षा के परितः। है। उसी द्रव्यमान के एक ऐसे खोखले एवं पतले बेलन की त्रिज्या, जिसका अपने अक्ष के परितः जड़त्व आघूर्ण । ही है, होगी
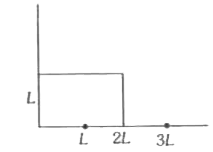
View Solutionचित्र में दिखायी गयी असममित किन्तु एकसमान छड़ जिसकी अनुप्रस्थ काट का क्षेत्रफल नगण्य है, के द्रव्यमान केन्द्र का स्थिति सदिश `vecr cm` होगा
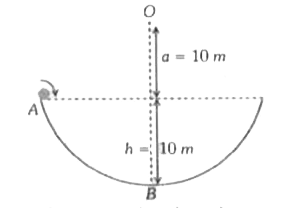
View Solutionचित्रानुसार 20g द्रव्यमान के एक कण को 5mls वक्र के अनुगत आरम्भिक वेग से बिन्दु A से छोडा जाता है। बिन्दु A की बिन्दु B से ऊँयाई है। यह कण घर्षणहीन पृष्ठ पर सरकता है। जब कण बिन्दु B पर पहुंचता है, तो इसका बिन्दुO के सापेक्ष कोणीय संवेग क्या होगा
View Solutionएक ठोस गोले का जड़त्व आघूर्ण, एक अक्ष के सापेक्ष, जो उसके व्यास के समान्तर तथा उससे x दूरी पर है, '!(x)'. है। निम्न में से कौन सा ग्राफ Ix) का x के साथ परिवर्तन को सही दर्शाता है
View Solution. यदि सूर्य के परितः तृतीय कक्ष में घूमते हुए द्रव्यमान m, के एक ग्रह का, सूर्य के केन्द्र के सापेक्ष, कोणीय संवेग L. है तो इसकी क्षेत्रीय गति होगी
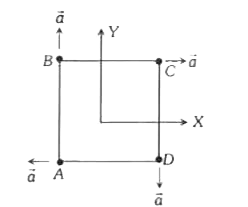
View Solutionद्रव्यमान `m_(A)=m,m_(B) =2m, m_(C) =3m` और `m_(0) =4m` वाले चार कण A, B,C और D एक वर्ग के कोनों पर रखे गये हैं। उनके त्वरण एकसमान परिमाण के हैं और दर्शाए गये चित्र के अनुसार हैं। कणों के द्रव्यमान केन्द्र का त्वरण है
View Solutionद्रव्यमान M और त्रिज्या R की एक वृत्तीय प्लेट का घनत्य `rho (r ) =rho_(0)r,` के अनुसार परिवर्तित हो रहा है जहाँ `rho _(0)` स्थिरांक है और । उसके केन्द्र से दरी है। प्लेट के लम्बवत और प्लेट की परिधि से जाने वाली अक्ष के परितः वृत्तीय प्लेट का जड़त्व आघूर्ण `I=aMR^(2)` है। गुणांक `alpha` का मान है
View Solutionएक ठोस गोला तथा एक ठोस बेलन जिनकी त्रिज्यायें समान है, एक आनत तल की तरफ समान रेखीय वेग से जा रहे हैं (चित्र देखें)। शुरू से अंत तक दोनों बिना फिसले लुढ़कते हुये चलते हैं। ये आनत तल पर अधिकतम ऊँचाई `h _(aph) `तथा `h_(eyl)` तक चढ़ पाते हैं तो अनुपात `(h _(sph))/(h_(eyl))` होगा

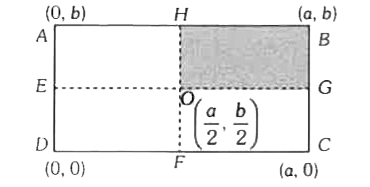
View Solutionद्रव्यमान M की एकसमान आयताकार पतली चदर ABCD जिसकी लम्बाई a तथा चौड़ाई b है, को चित्र में दिखाया गया है। यदि इसके आच्छादित भाग HBGO को काटकर हटा देते है तो बाकी चद्दर के द्रव्यमान केन्द्र का निर्देशांक होगा
View Solution0.3m लम्बाई के एक ठोस आयताकार डिब्बे के एक सिरे को 5m ऊँचे प्लेटफार्म के किनारे पर क्षैतिज पकड़ा हुआ है। जब उसे छोड़ते हैं तो लगभग क्षैतिज रहते हुए बहुत कम समय `tau =0.01s` में मेज पर से फिसल जाता है। जब यह जमीन पर गिरता है तो यह लगभग किस कोण (रेडियन में घूम जायेगा
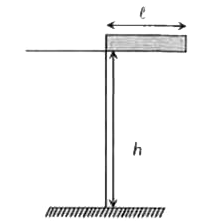
View Solutionनिम्न वस्तुएँ एक क्षतिज समतल से एक झुके हुए समतल पर लुढ़कते हुए (बिना फिसले) ऊपर की ओर चढ़ती है : (1) त्रिज्या R का एक वलय, (ii) त्रिज्या `R/2`का एक ठोस बेलन तथा (ii) त्रिज्या `R/4` का एक ठोस गोला। यदि प्रत्येक वस्तु के द्रव्यमान केन्द्र की गतियाँ झुके हुए समतल के निम्न बिन्दु पर बराबर हों, तो उनके द्वारा चड़ी गयी अधिकतम ऊँचाईयों का अनुपात होगा
View Solutionएक स्थिर क्षैतिज डिस्क अपनी अक्ष के परितः घूमने के लिये स्वतंत्र है। जब इस पर एक बल आघूर्ण लगाया जाता है, तो इसकी गतिज ऊर्जा `theta` के फलन में `ktheta ^(2)` से दी जाती है, जहाँ । परिश्रमण कोण है। यदि इसका जड़त्व आघूर्ण [ है तो इसका कोणीय त्वरण होगा
View Solutionएक पिण्ड का दिये गये अक्ष के परितः जड़त्व आघूर्ण `1.5 kgm ^(2)` है। आरम्भ में पिण्ड विरामावस्था में है। 1200J की घूर्णन गतिज ऊर्जा उत्पन्न करने के लिये, उसी अक्ष के परितः `20 rad //s^(2)` का कोणीय त्वरण कितने समयान्तराल तक लगाना होगा
View Solutionद्रव्यमान M तथा लम्बाई L की एक पतली छड़ कोणीय चाल से छड़ के लम्बवत् तथा उसके केन्द्र से जाने वाली अक्ष के परितः स्वतंत्र रूप से घूम रही है। दव्यमान m तथा नगण्य आकार की दो मणिकायें आरम्भ में छड़ के केन्द्र पर है। यह मणिकायें छड़ पर चलने को स्वतंत्र हैं। मणिकायें जब छड़ के विपरीत सिरों पर पहुँचती हैं, तो इस विन्यास की कोणीय चाल होगी
View Solutionद्रव्यमान M तथा त्रिज्या R की एक पतली डिस्क का प्रति इकाई क्षेत्रफल द्रव्यमान `sigma (r ) =kr ^(2)` है जहाँ । केन्द्र से दूरी है। डिस्क के केन्द्र से जाने वाली तथा इसके लम्बवत् अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionजड़त्व आघूर्ण `I_(1)` तथा `(I_(1))/(2)` की दो समअक्षीय डिस्क कोणीय वेग `omega _(1)` तथा `(omega_(i))/(2),` क्रमशः, से अपनी उभयनिष्ठ अक्ष के परितः घूम रहीं हैं। जब दोनों डिस्क को सटा दिया जाता है तो वे बराबर कोणीय वेग से घूमते हैं। यदि `E_(f)` तथा `E_(i)` अंतिम एवं प्रारम्भिक कुल कर्जाएँ हों तो `(E_(f) -E _(i))` का मान होगा
View Solutionद्रव्यमान m के एक पिण्ड का पथ निम्न है
`x =x _(0) + a cos omega _(1) t`
`y = y _(0) + b sin omega _(2) t`
`t =0` पर, मूलबिंदु के सापेक्ष पिण्ड पर लगने वाला जड़त्व आघूर्ण होगा
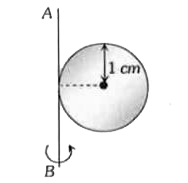
View Solution5g द्रव्यमान तथा 1cm त्रिज्या के धातु के एक सिक्के को एक पतली नगण्य द्रव्यमान की छड़ AB से चित्रानुसार जोड़ा जाता है। यह निकाय आरम्भ में स्थिरावस्था में है। इसे AB के परितः 5s तक 25 चक्कर प्रति सेकण्ड की गति से घुमाने के लिये नियत बलआघूर्ण का सन्निकट मान होगा
View Solutionद्रव्यमान M तथा त्रिज्या R के एक ठोस गोले को दो असमान हिस्सों में बाँटा जाता है। `(7M)/(8)` द्रव्यमान के पहले हिस्से को एक 2R त्रिज्या की एकसमान डिस्क में बदला जाता हैं बचे हुये हिस्से से एक एकसमान ठोस गोला बनाया जाता है। मानाकि `I_(1)` डिस्क का उसकी अक्ष के परितः जड़त्व आघूर्ण है तथा `I_(1) //I_(2)` नये गोले का उसके अक्ष के परितः जड़त्व आघूर्ण है। अनुपात `I_(1) //I_(2)` होगा
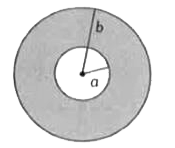
View Solutionकिसी वृत्ताकार डिस्क की त्रिज्या b है। इसमें एक छिद्र इसके केन्द्र पर बना है, जिसकी त्रिज्या a है चित्र देखिए। यदि डिस्क के प्रति-एकांक-क्षेत्रफल का द्रव्यमान, `((sigma _(0))/( r))` के अनुसार परिवर्तित होता है तो, इसके केन्द्र से गुजरने वाली अक्ष के परितः, डिस्क की विघूर्णन त्रिज्या होगी
View Solutionएक व्यक्ति (द्रव्यमान = M),L लम्बाई के एक झूले पर झूल रहा है। झूले का कोणीय आयाम `theta _(0)` है। झूले के अपने निम्नतम बिन्दु से गुजरते समय, वह व्यक्ति झूले पर खड़ा हो जाता है। यदि खड़े होने से उस व्यक्ति का द्रव्यमान केन्द्र `l( l lt lt L)` दूरी से विस्थापित हो जाता है, तो, व्यक्ति द्वारा किया गया कार्य होगा
View Solutionलम्बाई की, किसी एकसमान छड़ को, दौतिज समतल में, एक स्थिर कोणीय चाल से घुमाया जा रहा है। घूर्णन-अक्ष छड़ के एक सिरे से गुजरती है। यदि, इस घूर्णन के कारण, छड़ में उत्पन्न तनाव, अक्ष से x दूरी पर Tix) है तो, निम्नांकित में से कौनसा ग्राफ इसे सर्वाधिक निकट रूप से दर्शाता है
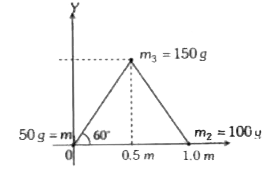
View Solution50g, 100 तथा 150g के तीन कणों को चित्रानुसार 1m भुजा वाले एक समबाहु त्रिभुज के कोनों पर रखा है। इस निकाय के द्रव्यमान केन्द्र {x तथा ) के निर्देशांक होंगे
View Solutionद्रव्यमान m=2 के एक कण की स्थिति, समय (t) के अनुसार,`vecr (t) =2 t veci -3 t^(2)vecj` है। इस कण का मूलबिन्दु के सापेक्ष 1 = 2 पर कोणीय संवेग होगा।
View Solutionद्रव्यमान 100 kg और 2m त्रिज्या की कोई चकती किसी क्षैतिज फर्श पर लुदकती है। इसके संहति केन्द्र की चाल 20cm/s है। इसे रोकने के लिये कितने कार्य की आवश्यकता होगी
View Solution4cm त्रिज्या और 2kg द्रव्यमान का कोई ठोस बेलन अपने अक्ष के परितः 3rpm की दर से घूर्णन कर रहा है। `2pi` परिक्रमण करने के पश्चात इसे रोकने के लिए आवश्यक बल आघूर्ण है
View Solution
CRITICAL THINKING OBJECTIVE QUESTIONS questions and complete solutions for chapter घूर्णी गति of ERRORLESS PHYSICS (HINDI) of Class 12