Complete Solutions to कोणीय संवेग of chapter घूर्णी गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | घूर्णी गति |
| ERRORLESS HINDI | कोणीय संवेग |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
सौर मण्डल में उपग्रहों की गति किसका उदाहरण है
View Solutionएक छल्ला जिसका द्रव्यमान M तथा त्रिज्या R है, केन्द्र 0 से होकर जाने वाले स्थिर ऊर्ध्वाधर अक्ष के चारों ओर `omega` कोणीय गति से घूम रहा है। इस समय पर `M/8` द्रव्यमान के दो बिन्दु द्रव्यमान छल्ले के केन्द्र पर विराम स्थिति में हैं। वे चित्र में दर्शाए अनुसार छल्ले पर लगी द्रव्यमान रहित दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकते हैं। किसी एक क्षण पर निकाय की कोणीय गति `8/9omega` है तथा एक विन्दु द्रव्यमान O से `3/5R`की दूरी पर है। इस क्षण दूसरे बिन्दु द्रव्यमान की 0 से दूरी होगी
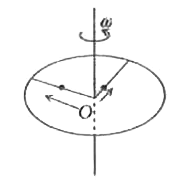
View SolutionM द्रव्यमान एवं । त्रिज्या की एक पतली वृत्ताकार वलय अपनी अक्ष के परितः नियत कोणीय वेग `omega` से घूम रही है। m द्रव्यमान के चार कण, वलय के दो लम्बवत् व्यासों के विपरीत बिन्दुओं पर धीरे से रख दिये जाते हैं, वलय का कोणीय वेग होगा
View Solutionस्थिति सदिश के कण का रेखीय संवेग p है। मूल बिन्दु के परितः इसके कोणीय संवेग के सम्बन्ध में निम्नलिखित में रो रात्य कथन है
View Solutionएक पतली क्षेतिज वृत्तीय चकती अपने केन्द्र से गुजर रही ऊधिर अक्ष पर घूर्णन कर रही है। चकती की धुरी के समीप बिन्दु पर एक कीड़ा विराम अवस्था में है। कीड़ा अब एक व्यास पर एक सिरे से दूसरे सिरे तक गतिशील होता है। कीड़े की यात्रा के दौरान चकती की कोणीय चाल
View Solutionकणों के एक निकाय का कोणीय संवेग संरक्षित रहता है
View Solutionएक क्षैतिज प्लेटफॉर्म अपने केन्द्र से गुजरने वाली ऊर्ध्वाधर अक्ष के परितः एकसमान कोणीय वेग से घूर्णन कर रहा है। किसी समय इसके केन्द्र पर 'm' द्रव्यमान का एक श्यान द्रव गिराया जाता है, जो कि फैलने के लिये स्वतंत्र है तथा अन्त में नीचे गिर जाता है। इस समयान्तराल में कोणीय वेग का मान
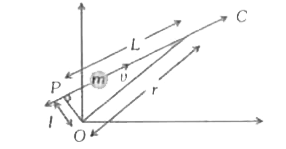
View Solutionm द्रव्यमान का एक कण PC रेखा के अनुदिश (चित्रानुसार) v वेग से गति करता है। बिन्दु O के परितः कण का कोणीय संवेग
View SolutionM द्रव्यमान एवं R त्रिज्या वाली एक पतली वृत्ताकार वलय किसी क्षैतिज तल में इसके केन्द्र से गुजरने वाले एवं तल के लम्बवत् अक्ष के परितः कोणीय वेग `omega` से घूर्णन कर रही है। यदि समान आकार परन्तु द्रव्यमान `M/4`की एक अन्य वलय पहली वाली वलय पर समक्षीय रख दी जाये तो निकाय का नया कोणीय वेग
View Solutionचिकने फर्श पर नृत्य कर रही एक नर्तकी अपने हाथों को सिकोड़े हुए 20 rad/sec के कोणीय वेग से ऊर्ध्वाधर अक्षा के परितः घूर्णन कर रही है। जब वह अपने हाथों को फैला देती है तो पूर्णन चाल घटकर 10 rad/sec हो जाती है। यदि नर्तकी का प्रारम्भिक जड़त्व आघूर्ण `I` हो तो नया जड़त्ल आपूर्ण होगा
View Solutionएक चकती कोणीय वेग `omega` से घूर्णन कर रही है। एक बच्चा इस पर धीरे से बैठ जाता है, तो संरक्षित रहेगा
View Solutionबल आघूर्ण आरोपित किये बिना एक पिण्ड का कोणीय वेग `omega_(1)` से `omega_(2)` हो जाता है, परन्तु यह परिवर्तन जड़त्व आघूर्ण में परिवर्तन होने के कारण होता है। दोनों स्थितियों में घूर्णन त्रिज्याओं का अनुपात होगा
View Solutionयदि पृथ्वी की त्रिज्या क्षण भर में सिकुड़कर वर्तमान त्रिज्या की आधी हो जाये, तो एक दिन में घण्टे होंगे
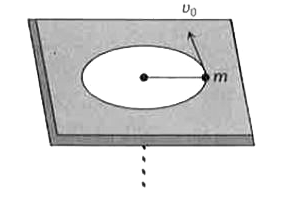
View Solution. M द्रव्यमान का एक पिंड (वस्तु), R. त्रिज्या के पथ में किसी चिकने क्षैतिज समतल के ऊपर `v_(0)` वेग से गति कर रहा है। यह पिंड एक डोरी (रस्सी) से जुड़ा है। जो समतल पर बने एक छिद्र से होकर गुजरती है जैसे कि आरेख में दर्शाया गया है। पिण्ड की गतिज ऊर्जा होगी।
View Solutionकणों के निकाय का कोणीय संवेग परिवर्तित होता है, यदि
View Solutionयदि एक पिण्ड पर बल, द्रव्यमान केन्द्र से दूर किसी बिन्दु पर कार्य करता है तब
View Solutionएक वस्तु की घूर्णीय गतिज ऊर्जा E तथा जड़त्व आघूर्ण `।` है। वस्तु का कोणीय संवेग होगा
View Solutionm द्रव्यमान का एक कण किसी तल में त्रिज्या r के वृत्तीय पथ पर घूम रहा है। इसका कोणीय संवेग L है। कण पर लगने वाले अभिकेंद्रिय बल का मान होगा
View Solutionरेखीय संवेग के आघूर्ण को कहते हैं
View Solutionलम्बाई की एक अवितान्य डोरी से बैंधे द्रव्यमान m के एक बाब को एक ऊर्ध्वाधर आधार से लटकाया जाता है। बाब ऊर्ध्वाधर पर कोणीय चाल `omega`rad/s से एक क्षैतिज वृत्त में घूर्णन करता है। निलंबन बिन्दु पर
View Solutionm द्रव्यमान व R त्रिज्या की एक चकत्ती की परिधि पर v वेग से एक कॉकरोच वामावर्त दिशा में चल रहा है चकती का अक्ष के परितः जड़त्व आघूर्ण । है और चकती `omega` कोणीय वेग से दाक्षिणावर्त घुमती है यदि कॉकरोच रूक जाये तब चकती का कोणीय वेग होगा
View Solutionकोणीय संवेग सरंक्षण के सिद्धान्त के अनुसार कोणीय संवेग
View Solutionएक कण की स्थिति `vecr = (hati + 2 hatj - hatk)` एवं संवेग `vecP -= (3hati + 4 hatj - 2 hatk)` द्वारा प्रदर्शित होते हैं। कोणीय संवेग लंबवत है
View Solutionएक कण कोणीय संवेग L से एकसमान वृतीय गति कर रहा है। यदि कण की गति की आवृत्ति दुगुनी एवं गतिज ऊर्जा आधी कर दी जाए तो कोणीय संवेग होगा
View Solutionएक पतली क्षेतिज वृत्तीय चकती अपने केन्द्र से गुजर रही ऊधिर अक्ष पर घूर्णन कर रही है। चकती की धुरी के समीप बिन्दु पर एक कीड़ा विराम अवस्था में है। कीड़ा अब एक व्यास पर एक सिरे से दूसरे सिरे तक गतिशील होता है। कीड़े की यात्रा के दौरान चकती की कोणीय चाल
View Solutionदो वस्तुओं के जड़त्व आघूर्ण उनकी घूर्णन अक्षा के सापेक्ष क्रमशः ! तथा 2 हैं। यदि उनकी घूर्णन गतिज ऊर्जाओं का मान समान हो, तो उनके कोणीय संवेगों का अनुपात होगा
View Solutionबाह्य बल आघूर्ण की अनुपस्थिति में किसी अक्ष के परितः परिक्रमा करने वाले पिण्ड के लिये कौनसी राशि नियत रहती है
View Solutionद्रव्यमान की एक विलियर्ड गेंद जिसकी त्रिज्या r है। एक क्षैतिज दिशा में केन्द्र से h ऊँचाई पर एक क्यू (लकड़ी) द्वारा हिट की जाती है तब उसका रेखीय वेग `v_(0)` प्राप्त होता है। गेंद द्वारा प्राप्त किया गया कोणीय वेग , होगा
View Solutionध्रुवीय बर्फ अचानक पिघल जाने से
View Solutionएक कण वृत्तीय मार्ग में गति कर रहा है। तब निम्न में से कौन सा कथन सत्य है
View Solutionकोणीय वेग `omega_(0)` से घूर्णन कर रहे द्रव्यमान m और त्रिज्या । के एक हुप को एक खुरपुरे क्षतिज राल पर रखा है। हूप के केन्द्र का प्रारम्भिक वेग शून्य है। जब यह स्लिप करना बन्द कर दे, तब हूप के कोन्द का वेग क्या होगा
View Solutionघूर्णन टेबिल पर खड़ा हुआ व्यक्ति अपने दोनों हाथों को फैलाकर उनमें भार पकड़े हुये है तथा घूर्णी गति कर रहा है। वह अचानक अपने हाथों को सिकोड़कर शरीर से सटा लेता है। कौन सा कथन सत्य है
View Solutionकिसी स्थिर बिन्दु के परितः किसी समतल में घूर्णन करते हुए एक पिंड के कोणीय संवेग की दिशा होती है|
View Solutionएक ठोस गोला अपने व्यास के परितः `omega` कोणीय वेग से घूम रहा है। यदि उसकी त्रिज्या प्रारम्भिक त्रिज्या की `1/n` गुना कर दी जाये तो उसका कोणीय वेग होगा
View Solutionयदि पृथ्वी को `6xx 10 ^(24)kg` का बिन्दु द्रव्यमान माना जाए, जो कि `1.5 xx 10 ^(8)` किमी की दूरी पर स्थित सूर्य के चारों ओर `T=3.14 xx 10 ^(7) s` में एक पूर्ण चक्कर लगा रहा है, तो सूर्य के चारों ओर पृथ्वी का कोणीय संवेग होगा
View Solutionकिसी पिण्ड का कोणीय संवेग किसका गुणनफल होता है
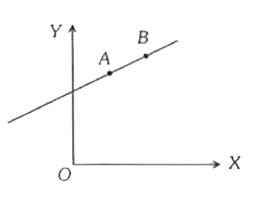
View Solutionm द्रव्यमान का एक कण XY तल पर Vवेग से रेखा AB के अनुदिश गति करता है (जैसा कि चित्र में दर्शाया गया है) यदि मूल बिन्दु 0 के सापेक्ष कोणीय संवेग `L_(A)` जब यह A पर है और`L_(B)` जब यह B पर है, तब सत्य कथन होगा ।
View Solutionआरेख में दर्शाये गये अनुसार, रस्सी के सिरे से जुड़ा हुआ एक छोटा सा पिण्ड, किसी घर्षण रहित मेज पर घूमता है। यदि रस्सी को खींचकर रस्सी के तनाव में वृद्धि कर दी जाये और रस्सी को इतना खींचा जाये कि, पिण्ड की (वृत्तीय) गति की त्रिज्या पहले से आधी हो जाये तो, पिंड की गतिज ऊर्जा
View Solutionएक पिण्ड नियत वेग से x-अक्ष के समान्तर सरल रेखा में गति करता है। मूल बिन्दु के सापेक्ष कोणीय संवेग होगा
View Solutionएक तैराक ऊँचाई से कूदते समय हवा में आसानी से कलाबाजी कर सकता है यदि वह
View Solutionएक तैराक ऊँचाई से कूदते समय हवा में आसानी से कलाबाजी कर सकता है यदि वह
View Solutionयदि घूर्णन कर रही किसी वस्तु का कोणीय संवेग 200% बढ़ा दिया जाए, तो इसकी गतिज ऊर्जा में वृद्धि होगी
View Solutionकक्षीय गति में, कोणीय संवेग सदिश होगा
View Solutionकिसी गोल चकती का इसके केन्द्र से जाने वाली तथा इसके तल के लंबवत् अक्ष के परितः, जड़त्व आघूर्ण `l_(2)` है। इस चकती को, `l_(1)` जड़त्व आघूर्ण वाली एक अन्य चकती, जो कि समान अक्ष के परितः `omega` कोणीय वेग से घूर्णन कर रही है, पर रखा जाता है। चकतियों के संयोजन का अंतिम कोणीय वेग होगा
View Solutionएक ठोस गोला किसी मुक्त स्थान में घूर्णन कर रहा है। यदि गोले के द्रव्यमान को नियत रखते हुए त्रिज्या को बढ़ाया जाए तो निम्न में से कौन सी राशि प्रभावित नहीं होगी
View Solutionकेन्द्रीय बल से घूमते हुये कण का कोणीय संवेग नियत रहता है, इसका कारण है
View Solutionकिसी तरणताल में कूदने से पूर्व तैराक अपने माथे को मोड़ लेता है, क्योंकि इससे
View Solutionकणों के निकाय का कोणीय संवेग संरक्षित नहीं रहता
View Solutionयदि किसी वस्तु की घूर्णन ऊर्जा 10 जूल है, तथा यदि इसका कोणीय संवेग सदिश घूर्णन अक्ष के साथ संपाती है व इस अक्ष के परितः उसका जड़त्व आघूर्ण `8xx 10 ^(-7) kg m ^(2)` है, वस्तु का कोणीय संवेग होगा
View Solutionयदि किसी वस्तु का द्रव्यमान जड़त्व आघूर्ण । तथा कोणीय वेग `omega `rad/sec है। तब उसके कोणीय संवेग L का मान होगा
View Solutionगदि पृश्नी को जिया तथा Mगमान का एक गोला माना जाए, तो इसकी घूर्णन अक्ष के परितः समयांतराल T के पदों में कोणीय संवेग का मान होगा
View Solutionएक व्यक्ति किसी वृत्तीय प्लेट के सिरे पर खड़ा हुआ है, जो कि इसके केंद्र से जाने वाली लम्बवत अक्ष के परितः नियत कोणीय चाल से घूर्णन कर रही है। यदि व्यक्ति त्रिज्या के अनुदिश अक्ष की ओर चलना प्रारंभ कर दे तो इसका कोणीय वेग
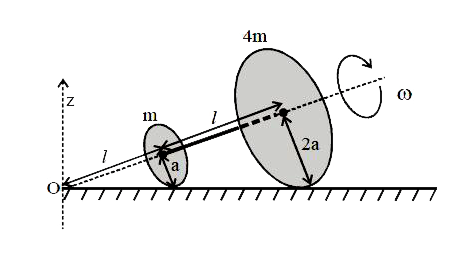
View Solutionm तथा 4m द्रव्यमान वाली दो पतली वृत्ताकार चत्रिकाएँ (discs), जिनकी त्रिज्याऐं क्रमशः a तथा 2a हैं, के केन्द्रों को `l = sqrt(24)a` लम्बाई की द्रव्यमान-रहित द्रढ़ (rigid) डंडी से जोड़ा गया है। इस समूह को एक मजबूत समतल सतह पर लिटाया गया है और फिसलाये बिना इस तरह से घुमाया गया है कि इसकी कोणीय गति डंडी के अक्ष के गिर्द `omega` है । पूरे समूह का बिन्दु `'omega'` के गिर्द कोणीय संवेग `vecL` है (चित्र देखिये) । निम्नलिखित में से कौनसा/कौनसे कथन सत्य है /हैं ?
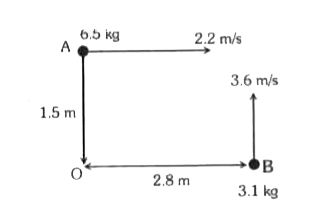
View Solutionदो कण A एवं B चित्रानुसार गति कर रहे हैं। इनका बिन्दु O से कूल कोणीय विस्थापन क्या होगा
View Solutionकिसी बिन्दु `vecr = 2 hati - 6 hatj - 12 hatk` पर एक बल `vecf = alpha hati + 3 hatj + 6 hatk` लग रहा है। तो `alpha` के किस मान के लिए मूल बिन्दु के परितः कोणीय संवेग सुरक्षित रहेगा
View Solutionघूर्णन करते हुए दो पिण्डों A तथा B के द्रव्यमान क्रमशः m तथा 2m और जडत्व आघूर्ण क्रमशः `I_(A)` तथा `I _(B) (I _(B) gtI _(A))` है। दोनों की घूर्णन गतिज ऊर्जाये बराबर है। यदि इनके कोणीय संवेग क्रमशः `L_(A)` तथा `L _(B)` हों, तब
View Solutionmद्रव्यमान का एक कण त्रिज्या r की वृत्तीय कक्षा में बल `vecF =- (K )/(r ^(2)) ` के प्रभाव में गतिमान है। कण का केन्द्र के सापेक्ष कोणीय संवेग होगा
View Solution
कोणीय संवेग questions and complete solutions for chapter घूर्णी गति of ERRORLESS PHYSICS (HINDI) of Class 12