Complete Solutions to Exercises of chapter GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GAUSS LAW |
| HC VERMA | Exercises |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
The electric field in a region is given by `vecE=3/5 E_0veci+4/5E_0vecj` with `E_0=2.0 xx 10^3 N C^(-1)`. Find the flux of this field through a recatngular surface of area `0.2m^2` parallel to the y-z plane.
View SolutionA charge Q is uniformly distributed over a rod of length `iota`. Condider a hypothetical cube of edge `iota` with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
View SolutionShow that there can be no net charge in a region in which the electric field is uniform at all points.
View SolutionThe electric field in a region is given by `vecE=E_0x/iota veci`. Find the charge contained inside a cubical volume bounded by the curfaced `x=0, x=alpha, y=0, y=alpha, z=0 and z= alpha`. Take `E_0= 5 xx 10^3 N C^(-1)`, `iota= 2cm and alpha=1 cm`.
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
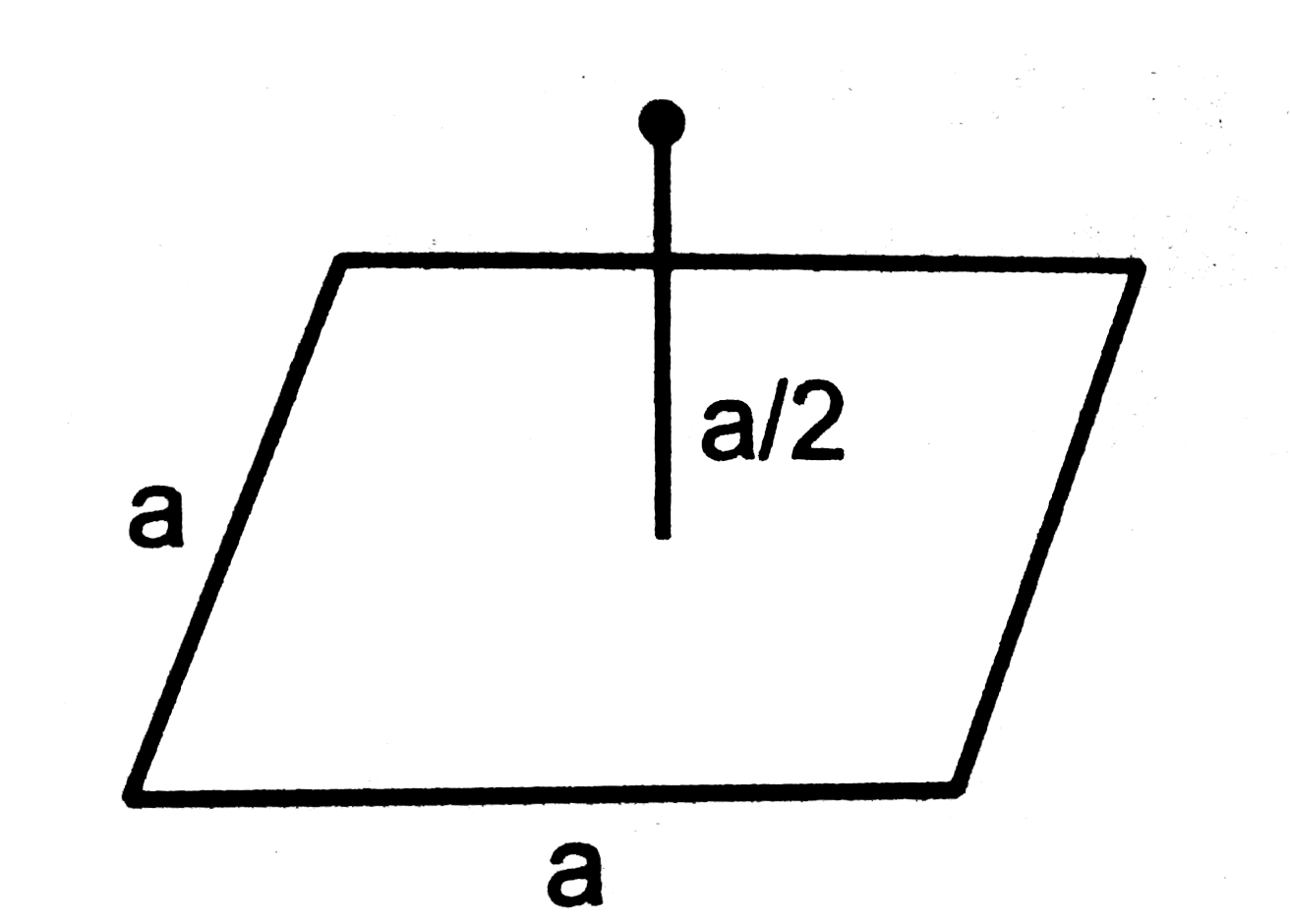
View SolutionA charge Q is placed at a distance `a/2` above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
View SolutionFind the fluz f the electric field through a spherical surface of radius R due to a charge of `10^(-7) C ` at the centre and another equal charge at a point 2R away from the centre (figure ).

View SolutionA charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

View SolutionA spherical volume contains a uniformaly distributed charge of density `2.0 xx 10^(-4) C /m^(3)`. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View SolutionThe radius of a gold nucleus (Z=79) is about `7.0*10^(-10) m`. Assume that the positive charge is distributed uniformly throughout the the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
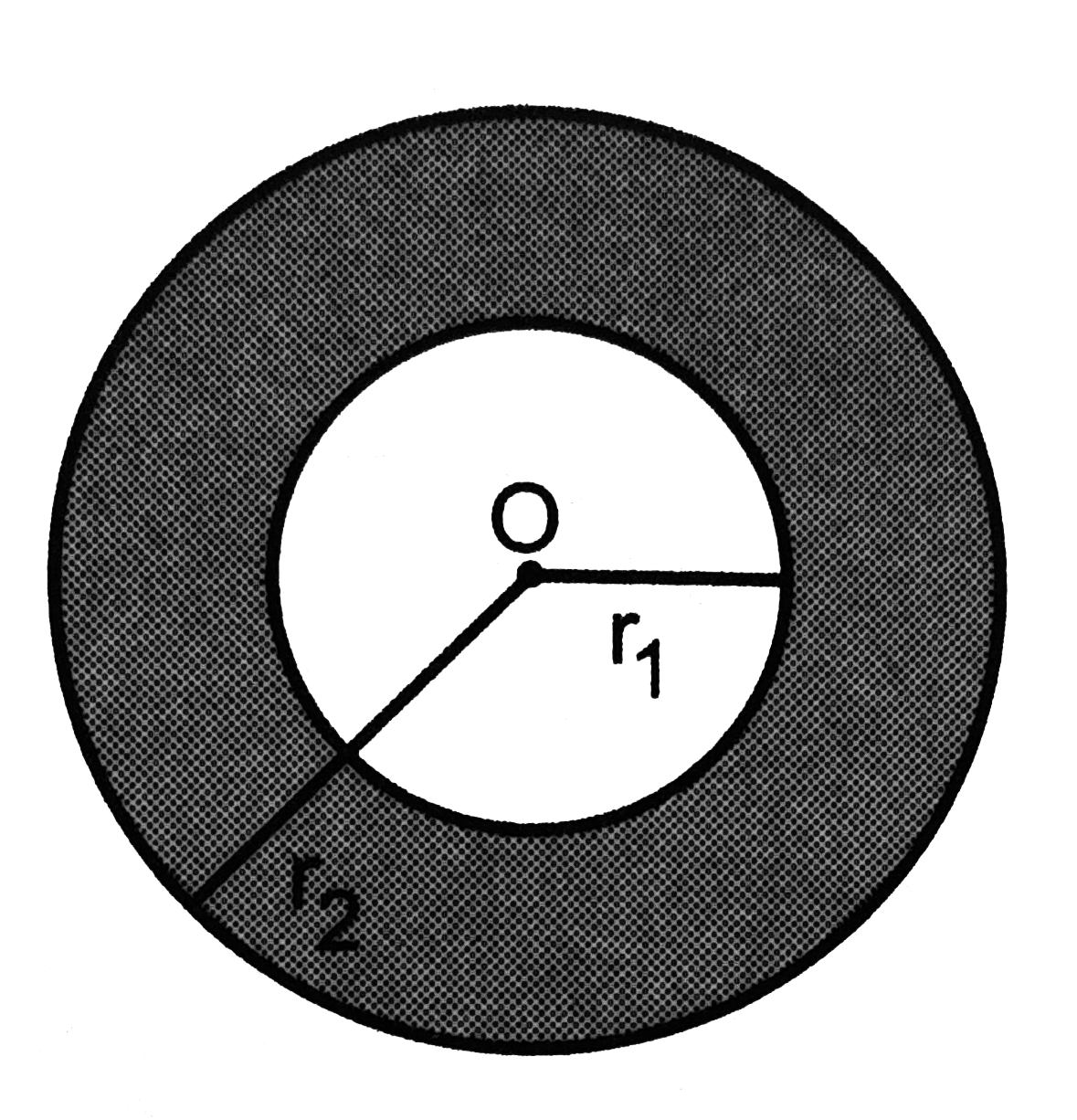
View SolutionA Charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii `r_1` and `r_2` (figure 30-E4). Find the electric field at a point P at a distance x away from the centre for `r_1ltxltr_2`. Draw a rough graph showing the electric field as a function of `x` for `0ltx lt2r_2`.
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View SolutionConsider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius `10^(-15)m`. The two 1s electrons make a spherical charge cloud at an average distance of `1.3 xx 10^(-11)` m from the nucleus, whereas the two 2s electrons make another spherical cloud at an average distance of `5.2 xx 10^(-11)` m from the nucleus. Find the electric field at (a) a point just inside the 1 s cloud and (b) a point just inside the 2s cloud.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density `2 xx 10^(-6) C m^(-1)`.
View SolutionA long cylindrical wire carries a positive charge of linear density `2.0 x 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
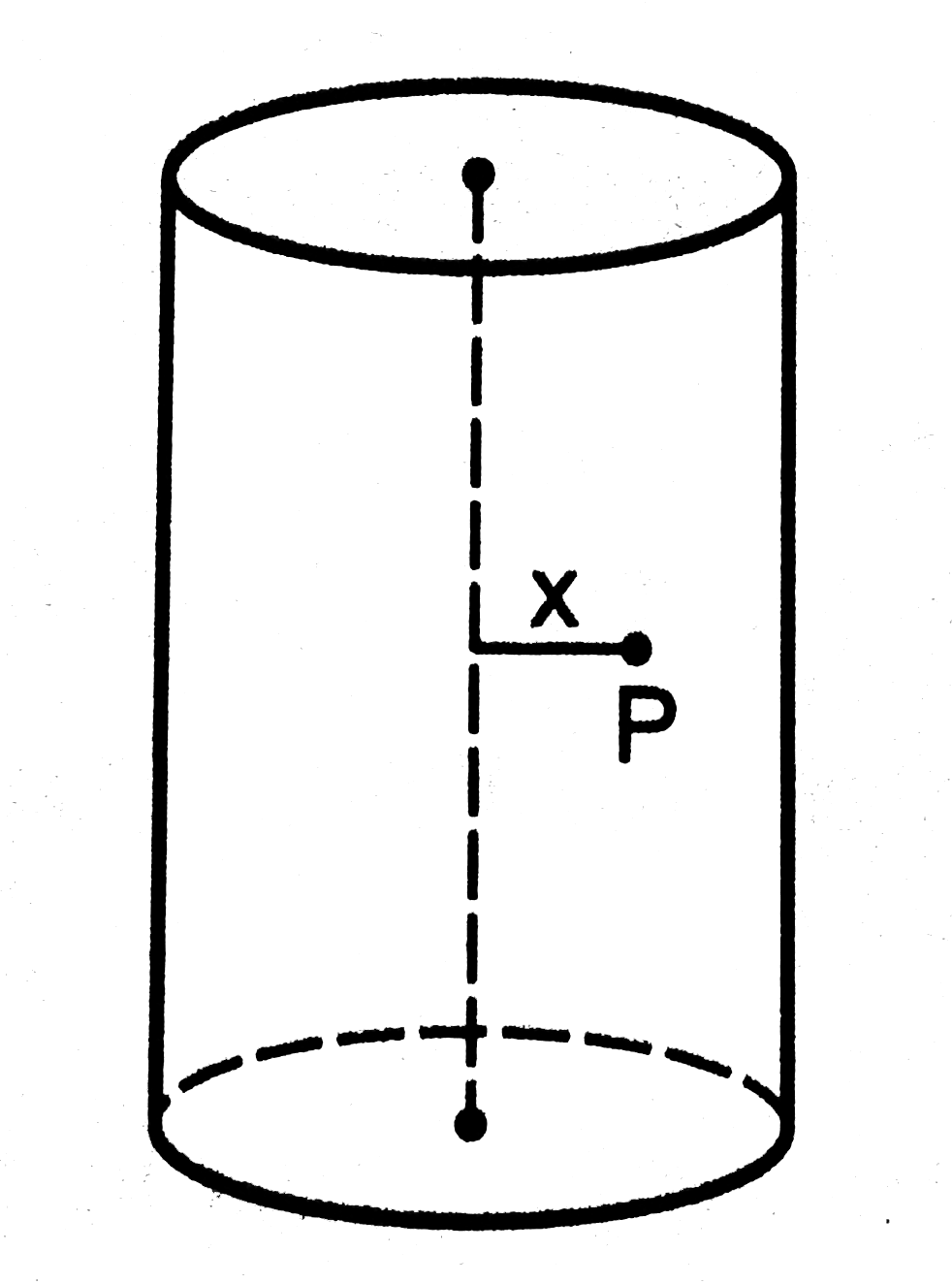
View SolutionA long cylindrical volume contains a uniformly distributed charge of density `rho`. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density `rho`. Find the electric field at a point P inside the plate, at a distance x from the central plane.
View SolutionA charged partical having a charge of `-2.0 xx 10^(-6) C` is placed close to a nonconducting plate having a surface charge density `4.0 xx 10^(-6) C m^(-2). Fine the force of attraction between the particle and the plate.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non conducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of `4.0 xx 10^ C`. In equilibrium, the thread make an angle of `60^0` with the vertical. Find the surface charge density on the plate.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of `4 xx 10^(-6) C`. In equilibrium, thread makes an angle of `60^(o)` with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use `sigma=7.5xx10^(-7) C/m^2`)
View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View SolutionTwo large conducting plates are placed parallel to each other nad they carry equal and opposite charges with surface density `sigma` as shown in figure (30-E6). Find the electric field (a) at the left of the plates, (b) in between the plates and © at the right of the plates.

View SolutionTwo large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X is given a charge Q whereas the other is neutral. Find (a) the surface charge density at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.

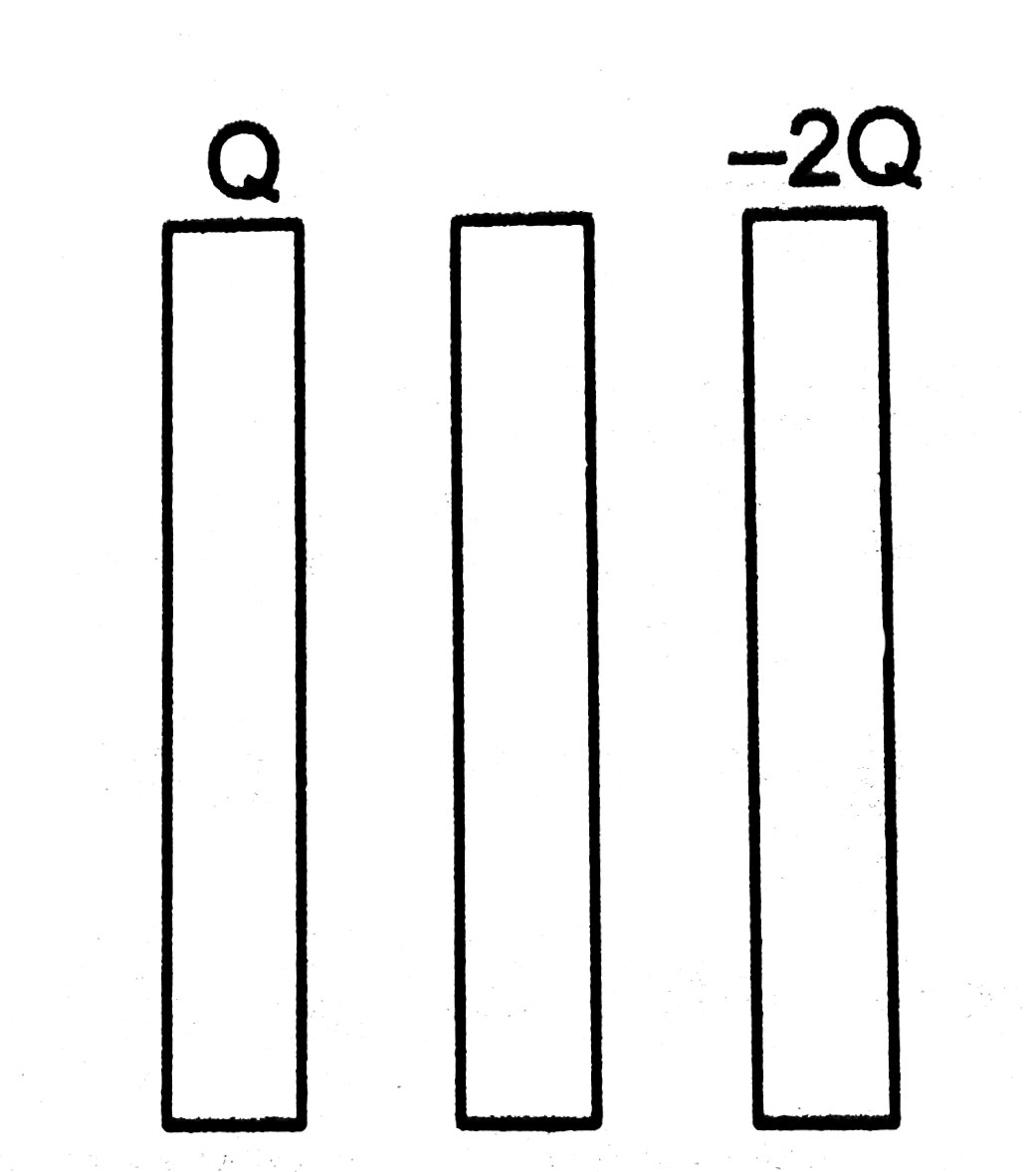
View SolutionThree identical metal plates with large surface areas are kept parallel to each as shown in figure (30-E8). The leftmost plate is given a charge Q, the rightmost a chrgear2Q and the middle one remains neutral. Find the charge appearing on the outer surface of the rightmost plate.
View Solution
Exercises questions and complete solutions for chapter GAUSS LAW of HC VERMA PHYSICS (ENGLISH) of Class 12