Complete Solutions to Multiple Choice Questions (MCQs) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| KUMAR PRAKASHAN | Multiple Choice Questions (MCQs) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If A and B are two events such that `P(A) gt 0` and `P(B) ne 1`, then `P(A | B')` is ……….
05:07View SolutionA study has been done to determine whether or not a certain drug leads to an improvement in symptoms for patients with a particular medical condition. The results are shown in the following table :
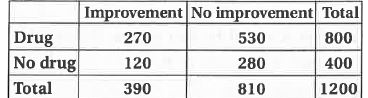
Based on this table, what is the probability that a patient shows improvement if it is known that the patient was given the drug ?03:12View SolutionA and B are two events such that `P(A) = (1)/(4), P(A | B)= (1)/(2) , P(B | A)= (2)/(3)`, then P(B)= ………….
02:21View SolutionIf two events A and B are such that `P(A')= 0.3, P(B)=0.5` and `P(A cap B) = 0.3`, then `P(B | A cup B')` is …………
03:39View SolutionThe probabilities of new purchased television and refrigerator will be working 10 years hence are `(7)/(15)` and `(7)/(10)` respectively. The probability that both will not be working 10 years hence is ………..
03:09View SolutionTwo unbiased dice are thrown. The probability that sum of the numbers appearing on the top face of two dice is 12, if 6 appears on the top face of first dice is ……….
02:20View SolutionIf A and B are two events such that `P(A) ne 0` and `P(B) ne 0`, then `P(A' | B')=` ……….
00:49View SolutionTwo unbiased dice are thrown. The probability that the sum of the numbers appearing on the top face of two dice is greater than 7, if 4 appear on the top face of first dice is ………..
02:30View SolutionIf A and B are two events such that `P(A) = (1)/(3), P(B) = (1)/(4)` and `P(A cap B) = (1)/(5)` , then `P(A' | B')` = ………..
02:46View SolutionIf A and B are two events such that `P(A) = (5)/(8), P(B) = (3)/(8)` and `P(A cup B) = (3)/(4)` then `P(A | B) `= ………..
01:13View SolutionIf `4P(A) = 6 P(B) = 10 P(A cap B) = 1 ` then `P(B | A) ` = ……….
00:51View SolutionIn a family having two children if one of the child is a girl, then the probability that other is also a girl is ………..
01:26View SolutionA and B are events such that `P(A')= 0.3, P(B) = 0.4 ` and `P(A cap B') = 0.5 ` then `P[B | (A cup B')] = ` …………
04:17View SolutionA coin is tossed three times is succession. If E is the event that there are at least two heads and F is the event in which first throw is a head, then `P(E | F)`= ………
03:29View SolutionIf `P(A | B) gt P(A)` then which of the following is true ?
00:51View SolutionChoose the correct answer:
If A and B are any two events such that P(A) + P(B) - P(A and B) = P(A), then01:02View SolutionIf `P(A)= 0.2, P(B) = 0.3 ` and ` P(A cup B) = 0.25` then ` P(B | A')` = ………..
02:18View SolutionIf `P(A) = 0.1, P(B) = 0.2 ` and `P(A cup B)= 0.25` then `P(A' | B')`= …………
01:15View SolutionIf `P(A) = 0.30, P(B) = 0.40 ` and `P( A cup B)= 0.60` then `P(B | A)=` ………..
01:05View SolutionOne card is selecting from the pack of 52 playing cards if A and B denotes that card is an ace and it is of square then `P(A|B)` = ………..
02:27View Solution`P(A' cup B') | C = `………………
01:01View SolutionA and B are events such that `P(A) ne 0, P(B) ne 1 ` then `P(barA // barB)=`………..
00:46View SolutionTwo unbaised coins are tossed. If one coin shows head, the probability that the other also shows head is ……..
01:25View SolutionIn a college 12 % students fails in mathematics, 25% fails in physics and 12% fails in both subjects. One student is selected at random. Then ………… is the probability of an event that student fail in Maths if he fail in physics.
01:55View SolutionComplementary events of E and F are E' and F' respectively if `0 lt P(F) lt 1` then …………
03:36View SolutionTwo cards are drawn in succession from a standard well shuffled pack of 52 card. What is the probability that both the cards are aces if the cards are drawn without replacement ?
01:53View Solutiona circular wheel with numbers 1 to 20 on its surface is rolled twice. What is the probability of getting two 13's ?
02:36View SolutionLet A and B be two events such that `P(A)= 0.4, P(A cup B)= 0.7` and `P(B)= p`. For what choice of p are A and B independent ?
01:28View SolutionA problem in mathematics is given to three students A, B, C and their respective probability of solving the problem is `(1)/(2), (1)/(3)` and `(1)/(4)`. Probability that the problem is solved is ………
02:51View SolutionThe probability that A speaks truth is `(4)/(5)`, while this probability for B is `(3)/(4)`. The probability that they contradict each other when asked to speak on an event is ……….
02:13View SolutionA company has three plants at which it produces a certain item. 30% are produced at plant A, 50% at plant B and remaining at plant C. Suppose that 1% , 4% and 3% of the items produced at plants A, B and C respectively are defective. If an item is selected at random from all of those produced, what is the probability that item was produced at plant B is defective ?
02:56View SolutionA problem of mathematics is given to three students and probability of solving the problem is ` (1)/(3), (1)/(3), (1)/(3)` respectively. The probability that at least one of them solves the problem is …………
03:31View SolutionLet `E_(1), E_(2), E_(3), ....,E_(n)` be independent events with respective probabilities `p_(1), p_(2), p_(3), ....,p_(n)`. The probability that none of them occurs is ……….
02:13View SolutionTwo cards are drawn at random from the well shuffled pack of 52 cards. If the first card is not replaced before the second card is drawn, then the probability of getting two aces is ………..
01:44View SolutionIf A and B are two independent events such that `P(A)= (1)/(2), P(B)= (1)/(5)`, then `P(A | (A cup B))`= ………
02:14View SolutionA small town has one fire engine and one ambulance available for emergencies. The probability that the fire engine is available when needed is 0.98 and the probability that the ambulance is available when called is 0.92. In the event of injury resulting from a building on fire, the probability that both the ambulance and the fire engine will be available is .........
02:21View SolutionIf A and B are two independent events such that `P(A cap B)= (3)/(25) ` and `P(A' cap B)= (8)/(25)` , then `P(B)=` ……….
01:55View SolutionA and B are independent events `P(A cap B)= 0.5` and `P(A)= 0.2` then `P(B)=` ……….
01:25View SolutionA purse contains 6 Silver coins and 3 Gold coins. Another purse contains 4 Silver coins and 5 Gold coins. A purse is selected at random and a coin is drawn from it. It's known that a coin is Gold then what is the probability that a Gold coin is selected from another `(II^(nd))` purse?
04:35View SolutionA fair coin is tossed n times, then what is the probability that H (Head) has appeared at least once ?
01:28View SolutionA building has two lifts. `L_(1)` and `L_(2)` are events when lifts are working. Probability `P(L_(1) ) = 0.01 = P(L_(2))* L_(1)` and `L_(2)` are independent events. What is the probability of atleast one lift is not working ?
04:27View SolutionSuppose A and B are two persons. The probability that A does the job is `(4)/(5)` and probability that B does the job is `(3)/(4)` . Then what is the probability that only one person does the job?
01:53View SolutionThree machines A, B and C produce respectively 30%, 50% and 20% of the total number of items of a factory. The percentage of defective output of these machines are 1%, 4% and 3% respectively. If an item is selected at random, find the probability that the item is non-defective.
05:00View SolutionLet X be the random variable with following probability distribution.
`therefore E(X^(2)) = ` ..............
 01:48View Solution
01:48View SolutionIf `P(A cap B)= (1)/(12)` and `P(A' cap B')= (1)/(2)` then `P(A) + P(B) =` .......
02:06View SolutionProbability of an event that newly purchase mobile and laptop will be in working condition after 8 years is `(7)/(12)` and `(7)/(9)` respectively. Then .... is the probability that both are not in working condition after 8 years.
02:42View SolutionA problem in mathematics is given to three students A, B, C and their respective probability of solving the problem is `(1)/(2),(1)/(3)` and `(1)/(4)` . Probability that the problem is solved is ........
02:51View SolutionProbability of an event that 10 persons `A_(1), A_(2), ..., A_(10)` with ages 70 years above expires in one year is `(1)/(2)`. Then ......... is the probability that person `A_(1)` expire first in one year.
05:32View SolutionIn one day match of 50 overs Sachin Tendulkar becomes out in odd numbers of over. Then ........ is the probability that he out in `9^(th)` over or over multiple of 9 = .........
View SolutionProbability of an event that one male person lives 10 years more is `(1)/(4)` . His wife lives 10 years more is `(1)/(3)` . Then of least one person lives has ......... probability.
View Solution4 American and 1 Indian couple Total 5 couples seats around the circular table at random. If it is given that each American seat near by his wife then ......... is the probability of an event that Indian person can seat near by his wife.
08:13View SolutionIn a city 40% persons have gray hair, 25% person have gray eyes and 15% person have gray hair as well as gray eyes. One person is selected at random then ........ is the probability of an event that person has gray hair and gray eyes.
03:20View Solution`f(x)= x^(3) + ax^(2) + bx + c` is real valued function in which a, b and c are selected by tossing one baised dice twice. Then ......... is the probability for f(x) becomes an increasing function.
05:36View SolutionIn box I and II there are 7 white 3 black, and 3 white, 7 black ball respectively. Now two balanced coins are tossed. If two heads comes up then box I is selected and one ball is drawn from it randomly. otherwise box II is selected and one ball is drawn from it randomly. Then ....... is the probability that selected ball is being white.
03:11View SolutionIn box X there are 4 red and 6 white balls and in box Y there are 3 red and 7 white balls. Now one ball is selected from box X and placed into box Y. Then from box Y one ball is drawn at random.
Then ....... is the probability that selected ball is of red colour and ball placed in box Y from box X is of white colour.02:31View SolutionIn bag X there are 2 white and 3 black balls and in bag Y there are 4 white and 2 black balls. One bag is selected at random and one ball is drawn from it. Then what is the probability that selected ball is white ?
02:02View SolutionFor the post of principal in school three persons A, B and C are candidates.
Probability of their appointment is in ratio `4 : 2 : 3`. If school time will changes to morning then probability of the appointment of candidate will be 0.3, 0.5 and 0.8 respectively. Then find probability of an event that school time changes to morning.View SolutionBox `B_(1)` contains 4 white and 6 black balls and box `B_(2)` contains 6 white and 4 black balls. Now one balanced coin is tossed. If two head comes up then 2 balls are drawn from box `B_(1)` other wise 2 white balls are drawn from Box `B_(2)`. Then find probability of an event that selected both balls are of white colour.
03:59View SolutionThere are 2 white and 3 red balls in box A and 4 white, 5 red balls in box B One box is selected at random and one ball is drawn from it. Then ......... is the probability that selected ball is of red colour.
02:28View SolutionThere are 16 coins in bag. Out of which 2 coins are defective having both sides head and remaining coins are good. One coin is selected at random from box and is tossed. Then ........ is the probability of event that head is obtained on it.
03:09View SolutionIn three boxes numbers of balls are 3 white & 1 black, 2 white and 2 black, 1 white and 3 black balls respectively. One ball is drawn from each box randomly. Then .......... is the probability of event that selected balls are 2 white and 1 black.
04:56View SolutionFor given events A and B if P(A) = 0.25 and P(B) = 0.50 probability that both event occurs together is 0.14. Then ........ is the probability of an event that A and B does not occurs.
01:47View SolutionThe probability of an event that student gets I, II and III grade in exam is `(1)/(10),(3)/(5)` and `(1)/(4)` respectively. Then ......... is the probability that he fails in exam.
02:08View Solution.......... is the probability of an event that there are 53 sundays in year 2019.
01:36View SolutionA person writes 4 letters and addresses on 4 covers. If these letters are inserted in covers randomly then ....... is the probability that all letters are not in proper cover.
02:54View SolutionPerson A speaks true in 75% and B speaks true in 80% then ....... is the probability that both contradict each other.
01:42View Solution3 integers are selected from the numbers 1 to 20. Then ........ is the probability that their product is an even number.
04:09View SolutionS is sample space if `P(A)= (1)/(3)P(B)` and `S= A cup B` Then P(A) = ....... Where A and B are mutually exclusive events.
01:36View SolutionFor events A and B `P(bar(A cup B))= (1)/(6), P(barA)= (1)/(4)` and `P(A cap B) = (1)/(4)` , Where `(barA)` is the complementary event of A then events A and B are
04:17View SolutionIn a vessel there are 5 red and 2 green balls. One ball is selected at random from it. If selected ball is green than one red ball is added in vessel and if selected ball is red then one green ball is added in vessel. Here selected ball is not placed back. Now second ball is drawn from it. Then ....... is the probability of event that second ball is of red colour.
05:08View SolutionOne balanced coin is tossed. If two head comes up then two balanced dice are tossed and sum of the numbers obtained on it is noted. If tail is obtain then one card is selected from the card numbered 1 to 9 and its number is noted. Then ....... is the probability of event that noted number from card is 7 or 8.
06:12View SolutionProbability of independent events is `P(A_(i))= (1)/(i+1)`. Where i = 1, 2, 3 ... n, probability of an event that at least one event occurs is ...............
05:05View SolutionA man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
03:08View SolutionA purse contains 4 copper and 3 silver coins while another purse contains 6 copper and 2 silver coins. A purse is drawn at random and coin is drawn. Then ....... is the probability that selected coin is of copper.
02:43View SolutionIn the box there are a white and b black balls. Two persons A and B takes ball one after the other and each time ball is placed back in box. Person A starts the game. If white ball is obtained then person A wins the game probability of winning game by person A is double then the winning probability of person B. Then `a : b =` .........
10:23View SolutionThe probability of an event that person hits the target is `(1)/(4)`. He hits target at least n times. The probability that to hit target n times is more than `(2)/(3)` then minimum value of n is ........
06:18View SolutionEach element of the second order determinant is 1 and - 1 then ....... is the probability that value of determinant is not zero.
02:35View SolutionA coin is tossed 2n times. During the toss any person can't get head and tail with equal numbers. Its probability is ........
04:08View SolutionFor events E and F if `P(E) le P(F) ` and `P(E cap F) gt 0` then …………
03:42View SolutionThe probability that a student is not a swimmer is `(4)/(5)`. The probability that out of 5 students exactly 4 are swimmers is ………..
01:59View SolutionThe probability distribution of random variable X is as follows.
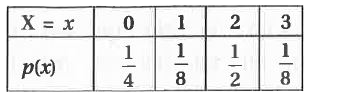
Then possible value of `E(2X +3)` ………….02:03View SolutionMean and variance of binomial distribution of random variance X are 4 and 2 respectively then `P(X = 1) = ` ……….
02:26View SolutionIn experiment probability that event A occurs in first trail is 0.4 then ………. is the probability that in three independent trial event A occurs.
03:15View SolutionProbability distribution of random variable X is as follows :
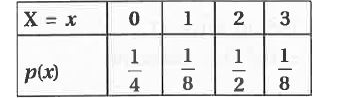
Then variance of `g(X) = 2X + 3` ……….06:36View SolutionA random variable X has the probability distribution:

For the events E = { X is a prime number } and `F = { X lt 4}`, the probability `P(E cup F)` is ………..03:21View SolutionIf a random variable X can take all non- negative integral values and the probability that X takes the value r is proportional to `alpha^(r)(0 lt alpha lt 1)` then `P(X = 0)` is ………..
04:52View SolutionThe mean and standard deviation of a random variable X are 10 and 5 respectively. Match the following.
 05:36View Solution
05:36View SolutionThe probability distribution of a random variable X is given below :
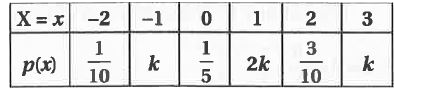
The value of k is ……….01:45View SolutionMean of the following probability distribution is …………
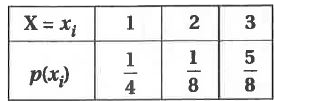 01:28View Solution
01:28View SolutionA fair dice is rolled 6 times. If "getting an even number" is a success the probability of 5 successes is …………..
02:07View SolutionA fair dice is rolled 6 times. If "getting a prime number" is a "success" , the probability of no seccess is …………
02:43View SolutionA bag consists of 10 balls each marked with one e digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
01:13View SolutionMean of the binomial distribution is 100 then it standard deviation lies in ………… interval.
02:33View SolutionIn a box there are 100 electric bulbs out of which 10 are defective. 5 bulbs are selected from it then ………..is the probability that bulb is defective.
02:17View SolutionMean and variance of one binomial distribution are `(4)/(3)` and `(20)/(21)` respectively then p = ………….. where p is parameter.
01:47View SolutionProbability distribution of a discrete random variable X is given in the following table.

1) Find the probability of random variable X assuming negative values.
2) Find the value of `P(0 le x le 3)`02:05View SolutionMean and variance of binomial distribution are 3 and 2 respectively then parameter n is ………..
01:54View SolutionThe probability function of the binomial distribution is `P(x)= ((6), (x))p^(x)q^(6-x), x= 0, 1, 2, ....., 6.` If `2P(2) = 3P(3)` then value of q is ……….
02:53View SolutionLet X be the random variable with following probability distribution.
`therefore E(X^(2))= ...... `
 02:42View Solution
02:42View SolutionThe mean and standard deviation of a random variable X are given by E(X) = 5 and `sigma_(x)=3` respectively, then
`(1) E(X^(2))=…….`
(2) `E[(3X-2)^(2)]= ……….`
(3) `V(3-2X)= …………`04:33View Solution
Multiple Choice Questions (MCQs) questions and complete solutions for chapter PROBABILITY of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12
All Exercises from KUMAR PRAKASHAN Class 12 MATHS PROBABILITY
- EXERCISE -13.1
- EXERCISE -13.2
- EXERCISE -13.3
- EXERCISE -13.4
- EXERCISE -13.5
- MISCELLANEOUS EXERCISE 13
- Multiple Choice Questions (MCQs)
- Practice Paper - 13 (Section - A (Choose the correct option))
- Practice Paper - 13 (Section - B (Answer the following questions))
- Practice Paper - 13 (Section - C (Answer the following questions))
- Practice Paper - 13 (Section - D (Answer the following questions))
- Practice Work
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook Illustrations for Practice Work
