Complete Solutions to Textbook Illustrations for Practice Work of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| KUMAR PRAKASHAN | Textbook Illustrations for Practice Work |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
If `P(A)= (7)/(13), P(B)= (9)/(13) ` and `P( A cap B) = (4)/(13)` evaluate `P(A | B)`
00:39View SolutionA couple has two children,
(i) Find the probability that both children are males, if it is known that at least one of the children is male.
(ii) Find the probability that both children are females, if it is known that the elder child is a female.04:30View SolutionTen cards numbered 1 to 10 are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3, what is the probability that it is an even number?
02:03View SolutionIn a school there are 1000 students out of which 430 are girls. It is known that 10 % girls are studying in class XII. Find the probability of an event that randomly selected student studies in class XII given that selected student is girl.
03:24View SolutionA die is thrown three times. Events A and B are defined as below:
A : 4 on the third throw
B : 6 on the first and 5 on the second throw
Find the probability of A given that B has already occurred.03:13View SolutionA dice is thrown twice and the sum of the numbers appearing is observed to be 6. What is the conditional probability that the number 4 has appeared at least once ?
02:23View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4' given that there is at least one tail.
07:14View SolutionAn urn contains 10 black and 5 white balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are black ?
01:16View SolutionThree cards are drawn successively, without replacement from a pack of 52 well shuffled cards. What is the probability that first two cards are kings and the third card drawn is an ace?
02:09View SolutionA die is thrown. If E is the event the number appearing is a multiple of 3' and F be the event 'the number appearing is even' then find whether E and F are independent ?
02:27View SolutionAn unbiased die is thrown twice. Let the event A be 'odd number on the first throw' and B the event 'odd number on the second throw'. Check the independence of the events A and B.
02:59View SolutionThree coins are tossed simultaneously. Consider the event E 'three heads or three tails', F 'at least two heads' and G ‘at most two heads'. Of the pairs (E,F), (E,G) and (F,G), which are independent? which are dependent?
04:48View SolutionProve that if E and F are independent events, then so are the events E and F'.
02:23View SolutionIf A and B are two independent events, then the probability of occurrence of at least one of A and B is given by 1- P(A') P(B').
02:55View SolutionA person has undertaken a construction job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
03:28View SolutionBag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag II.
03:43View SolutionGiven three identical boxes I, II and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in the box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?
03:54View SolutionSuppose that the reliability of a HIV test is specified as follows:
Of people having HIV, 90% of the test detect the disease but 10% go undetected. Of people free of HIV, 99% of the test are judged HIV-ive but 1% are diagnosed as showing HIV+ive. From a large population of which only 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist reports `"him" // "her"` as HIV+ive. What is the probability that the person actually has HIV?05:03View SolutionIn a factory which manufactures bolts, machines A, B and C manufacture respectively 25%, 35% and 40% of the bolts. Of their outputs, 5, 4 and 2 percent are respectively defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by the machine B ?
06:13View SolutionA doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport are respectively `(3)/(10), (1)/(5), (1)/(10)` and `(2)/(5)`. The probabilities that he will be late are `(1)/(4), (1)/(3)` and `(1)/(12)`, if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. What is the probability that he comes by train?
05:16View SolutionA man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
03:08View SolutionA person plays a game of tossing a coin thrice. For each head, he is given Rs 2 by the organiser of the game and for each tail, he has to give Rs 1.50 to the organiser. Let X denote the amount gained or lost by the person. Show that X is a random variable and exhibit it as a function on the sample space of the experiment.
03:49View SolutionA bag contains 2 white and 1 red balls. One ball is drawn at random and then put back in the box after noting its colour. The process is repeated again. If X denotes the number of red balls recorded in the two draws, describe X.
02:30View SolutionTwo cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Find the probability distribution of the number of aces.
03:59View SolutionFind the probability distribution of number of doublets in three throws of a pair of dice.
04:09View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where k is some unknown constant.
`P(X=x)={{:(0.1, "if "x =0),(kx, "if "x = 1 or 2 ),(k(5-x), "if " x=3 or 4),(0,"otherwise"):}`
(a) Find the value of k.
(b) What is the probability that you study at least two hours ? Exactly two hours? At most two hours?03:09View SolutionLet a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
02:41View SolutionFind the variance of the number obtained on a throw of an unbiased die.
02:53View SolutionTwo cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean, variance and standard deviation of the number of kings.
05:05View SolutionSix balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether or not the trials of drawing balls are Bernoulli trials when after each draw the ball drawn is (i) replaced (ii) not replaced in the urn.
06:39View SolutionIf a fair coin is tossed 10 times, find the probability of
(i) exactly six heads
(ii) at least six heads
(iii) at most six heads04:28View SolutionTen eggs are drawn successively with replacement from a lot containing 10% defective eggs. Find the probability that there is at least one defective egg.
03:05View SolutionColoured balls are distributed in four boxes as shown in the following table :
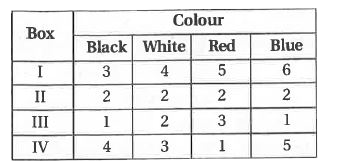
A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the box III ?03:15View SolutionFind the mean of the Binomial distribution `B(4, (1)/(3))`
01:00View SolutionThe probability of a shooter hitting a target is `(3)/(4)`. How many minimum number of times must `"he" // "she"` fire so that the probability of hitting the target at least once is more than 0.99?
02:08View SolutionA and B throw a die alternatively till one of them gets a '6' and wins the game. Find their respective probabilities of winning, if A starts first.
02:15View SolutionIf a machine is correctly set up, it produces 90% acceptable items. If it is incorrectly set up, it produces only 40% acceptable items. Past experience shows that 80% of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.
04:14View Solution
Textbook Illustrations for Practice Work questions and complete solutions for chapter PROBABILITY of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12
All Exercises from KUMAR PRAKASHAN Class 12 MATHS PROBABILITY
- EXERCISE -13.1
- EXERCISE -13.2
- EXERCISE -13.3
- EXERCISE -13.4
- EXERCISE -13.5
- MISCELLANEOUS EXERCISE 13
- Multiple Choice Questions (MCQs)
- Practice Paper - 13 (Section - A (Choose the correct option))
- Practice Paper - 13 (Section - B (Answer the following questions))
- Practice Paper - 13 (Section - C (Answer the following questions))
- Practice Paper - 13 (Section - D (Answer the following questions))
- Practice Work
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook Illustrations for Practice Work
