Complete Solutions to Solutions of NCERT Exemplar Problems (Long Answer Type Questions) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| KUMAR PRAKASHAN | Solutions of NCERT Exemplar Problems (Long Answer Type Questions) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
An urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.
06:35View SolutionThree bags contain a number of red and white balls as follows:

The probability that bag i will be chosen and a ball is selected from it is `(i)/(6)`, i = 1, 2, 3. What is the probability that,
(i) a red ball will be selected ?
(ii) a white ball is selected ?05:48View SolutionThree bags contain a number of red and white balls as follows:
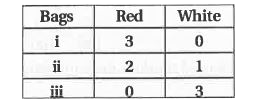
If a white ball is selected, what is the probability that it came from (i) Bag II (ii) Bag III.07:23View SolutionA shopkeeper sells three types of flower seeds `A_(1), A_(2)`, and `A_(3)`. They are sold as a mixture, where the proportions are 4:4:2 respectively. The germination rates of the three type of seeds are 45%, 60% and 35%. Calculate the probability
(i) Of a randomly chosen seed to germinate
(ii) That it will not germinate given that the seed is of type `A_(3)`.
(iii) That it is of the type `A_(2)` given that a randomly chosen seed does not germinate.09:06View SolutionA letter is known to have come either from word TATA NAGAR or from CALCUTTA, On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR ?
06:43View SolutionThere are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the `1^(st)` bag, but it shows up any other number, a ball is chosen from the `2^(nd)` bag. Find the probability of choosing a black ball.
04:52View SolutionThe three urns having the numbers of white and black balls are given below :

The probability of chosing every urn is equl. A ball is chosen randomly from the urn is found to be white. Then find the probability that the ball chosen was that form urn-2.06:38View SolutionBy examining the chest X-ray probability that T.B. is detected when person is actually suffering is 0.99. The probability that doctor diagnoses incorrectly that person has T. B. on the basis of X-ray is 0.001. In certain city 1 to 1000 persons suffering from T.B. A person is selected at random is diagnosed to have a T.B. what is the chance he has actually T.B. ?
05:00View SolutionAn item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A ?
05:11View SolutionLet X be a discrete random variable whose probability distribution is defined as follows:
`P(X=x)={(k(x+1)",",x="1, 2, 3, 4"),(2kx",",x="5,6,7"),(0"", "Otherwise"):}`
Where k is a constant. Calculate (i) the value of k (ii) E(X) (iii) Standard deviation of X.03:45View SolutionThe probability distribution of a discrete random variable X is given as under :
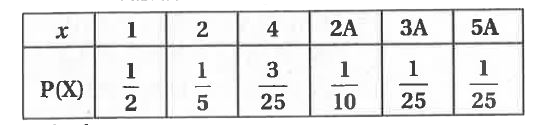
Calculate :
(i) The value of A if E(X) = 2.94 (ii) Variance of X06:30View SolutionThe probability distribution of a random variable X is given as under :
`P(X=x)={(kx^(2)",",x="1, 2, 3"),(2kx",",x="4,5,6"),(0"", "Otherwise"):}`
where k is a constant. Calculate (i) E(X), (ii) `E(3X^(2))` and (iii) `P(x ge 4)`.06:40View SolutionA bag contains (2n + 1) coins. It is known that n of these coins have a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is `(31)/(42)`, then determine the value of n.
04:56View SolutionTwo cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X, where X is the number of aces.
07:49View SolutionA dice is tossed twice. A 'success' is getting an even number on a toss. Find the variance of the number of successes.
05:02View SolutionThere are 5 cards numbered 1 to 5, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on two cards drawn. Find the mean and variance of X.
09:58View Solution
Solutions of NCERT Exemplar Problems (Long Answer Type Questions) questions and complete solutions for chapter PROBABILITY of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12
All Exercises from KUMAR PRAKASHAN Class 12 MATHS PROBABILITY
- EXERCISE -13.1
- EXERCISE -13.2
- EXERCISE -13.3
- EXERCISE -13.4
- EXERCISE -13.5
- MISCELLANEOUS EXERCISE 13
- Multiple Choice Questions (MCQs)
- Practice Paper - 13 (Section - A (Choose the correct option))
- Practice Paper - 13 (Section - B (Answer the following questions))
- Practice Paper - 13 (Section - C (Answer the following questions))
- Practice Paper - 13 (Section - D (Answer the following questions))
- Practice Work
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook Illustrations for Practice Work
