Complete Solutions to Solutions of NCERT Exemplar Problems (Short Answer Type Questions) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| KUMAR PRAKASHAN | Solutions of NCERT Exemplar Problems (Short Answer Type Questions) |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
For a loaded die, the probabilities of outcomes are given as under :
`P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1` and `P(4) = 0.3.`
The die is thrown two times. Let A and B be the events, 'same number each time', and 'a total score is 10 or more', respectively. Determine whether or not A and B are independent.07:30View SolutionFor a loaded die, the probabilities of outcomes are given as under :
`P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1` and `P(4) = 0.3.`
The die is thrown two times. Let A and B be the events, 'same number each time', and 'a total score is 10 or more', respectively. Determine whether or not A and B are independent.07:30View SolutionThe probability that atleast one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate `P(barA ) + P(barB)`.
02:16View SolutionA bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that atleast one of the three marbles drawn be black, if the first marble is red ?
04:00View SolutionTwo dice are thrown together and the total score is noted. The events E, F and G are 'a total of 4', 'a total of 9 or more', and 'a total is divisible by 5', respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.
10:00View SolutionExplain why the experiment of tossing a coin three times is said to have binomial distribution.
04:05View SolutionIf A and B are two events such that `P(A) = (1)/(2), P(B)= (1)/(3)` and `P(Acap B)= (1)/(4)`. Find :
(i) `P(A//B)` (ii) `P(B // A)` (ii)` P(A'//B)` (iv)`P(A'//B')`04:11View SolutionThree events A, B and C have probabilities `(2)/(5), (1)/(3) ` and `(1)/(2)` respectively. Given that `P(A cap C)=(1)/(5), P(B cap C)=(1)/(4)` find the values of `P(C//B)` and `P(A' cap C')`.
02:17View SolutionLet `E_(1)` and `E_(2)` be two independent events such that `P(E_(1)) = P_(1)` and `P(E_(2)) = P_(2)`. Describe in words of the events whose probabilities are :
(i) `P_(1)*P_(2)` (ii) `(1-P_(1))* P_(2)` (iii) `1-(1-P_(1))*(1-P_(2))` (iv) `P_(1) +P_(2) - 2P_(1)*P_(2)`08:07View SolutionA discrete random variable X has the probability distribution given as below:

(i) Find the value of k
(ii) Determine the mean of the distribution.03:12View SolutionProve that,
` P(A)=P(A cap B) +P(A cap barB)`02:56View SolutionProve that
`P(A cup B) = P(A cap B)+P(A cap barB)+P(barA cap B)`04:22View SolutionIf X is the number of tails in three tosses of a coin, determine the standard deviation of X.
07:01View SolutionIn a dice game, a player pays a stake of ₹ 1 for each throw of a die. She receives ₹ 5 if the die shows a 3, ₹ 2 if the die shows a 1 or 6 and nothing otherwise. What is the player's expected profit per throw over a long series of throws ?
05:46View SolutionThree dice are thrown at the sametime. Find the probability of getting three two's, if it is known that the sum of the numbers on the dice was six.
03:52View SolutionSuppose 10,000 tickets are sold in a lottery each for ₹ 1. First prize is of ₹ 3000 and the second prize is of ₹ 2000. There are three third prizes of ₹ 500 each. If you buy one ticket, what is your expectation ?
04:22View SolutionA bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.
04:10View SolutionBag-I contains 3 black and 2 white balls, Bag-II contains 2 black and 4 white balls. A bag and a ball is selected at random. Determine the probability of selecting a black ball.
03:59View SolutionA box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then, another ball is drawn at random. What is the probability of second ball being blue ?
04:29View SolutionFour cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are kings ?
00:55View SolutionIf a die is thrown 5 times. Then find the probability that an odd number will come up exactly three times.
01:18View SolutionTen coins are tossed. Then what is the probability of getting atleast 8 heads ?
04:27View SolutionThe probability of a man hitting a target is 0.25. He shoots 7 times, then what is the probability of his hitting atleast twice ?
04:44View SolutionA lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then what is the probability that there will be atleast one defective watch ?
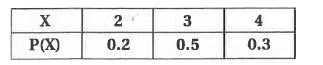
01:19View SolutionConsider the probability distribution of a random variable X:

Calculate (i) `V((X)/(2))` (ii) Variance of X.03:58View SolutionThe probability distribution of a random variable X is given below:
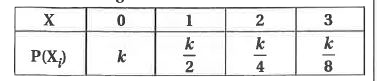
(i) Determine the value of k.
(ii) Determine `P(X le 2)` and `P(X gt 2)`
(ii) Find `P(X le 2) +P(X gt 2)`.03:45View SolutionFor the following probability distribution determine standard deviation of the random variable X.
 02:31View Solution
02:31View SolutionA biased die is such that `P(4) = (1)/(10)` and other scores being equally likely. The die is tossed twice. If X is the 'number of fours seen', then find the variance of the random variable X.
05:16View SolutionA dice is thrown three times. Let X be 'the number of two seen'. Find the expectation of X.
04:56View SolutionTwo biased dice are thrown together. For the first dice `P(6) = (1)/(2)` , the other scores being equally likely while for the second dice, `P(1) = (2)/(5)` and the other scores are equally likely. Find the probability distribution of 'the number of ones seen'.
04:32View SolutionTwo probability distributions of the discrete random variables X and Y are given below.

Prove that `E(Y^(2)) = 2E(X)`.02:22View SolutionA factory produces bulbs. The probability that any one bulb is defective is `(1)/(50)` and they are packed in 10 boxes. From a single box, find the probability that,
(i) none of the bulbs is defective
(ii) exactly two bulbs are defective
(iii) more than 8 bulbs work properly.06:35View SolutionSuppose you have two coins which appear identical in your pocket. You know that, one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin ?
04:12View SolutionSuppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed 30% of the people have blood group O. If a left handed person is selected at random, what is the probability that he/she will have blood group O ?
06:34View SolutionTwo natural numbers r, s are drawn one at a time, without replacement from the set S = {1, 2, 3, 4, ....., n}. Find `P(r le p//s le p)`, where `p in S.`
06:55View SolutionFind the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
07:12View SolutionThe random variable X can take only the values 0, 1, 2. Given that `P(X = 0) = P(X = 1) = p` and that `E(X^(2)) = E(X)`, find the value of p.
02:41View SolutionFind the variance of the distribution:
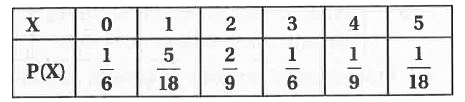 03:07View Solution
03:07View SolutionA and B throw a pair of dice alternately. A wins the game if he gets a total of 6 and B wins if she gets a total of 7. It A starts the game, then find the probability of winning the game by A in third throw of the pair of dice.
04:38View SolutionTwo dice are tossed. Find whether the following two events A and B are independent :
`A = {(x, y): x + y = 11}` and `B = {(x, y): x ne 5}`
where (x, y) denotes a typical sample point.05:50View Solution
Solutions of NCERT Exemplar Problems (Short Answer Type Questions) questions and complete solutions for chapter PROBABILITY of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 12
All Exercises from KUMAR PRAKASHAN Class 12 MATHS PROBABILITY
- EXERCISE -13.1
- EXERCISE -13.2
- EXERCISE -13.3
- EXERCISE -13.4
- EXERCISE -13.5
- MISCELLANEOUS EXERCISE 13
- Multiple Choice Questions (MCQs)
- Practice Paper - 13 (Section - A (Choose the correct option))
- Practice Paper - 13 (Section - B (Answer the following questions))
- Practice Paper - 13 (Section - C (Answer the following questions))
- Practice Paper - 13 (Section - D (Answer the following questions))
- Practice Work
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook Illustrations for Practice Work
