Complete Solutions to Multiple Choice Questions(LEVEL I) of chapter UNIFORM CIRCULAR MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | UNIFORM CIRCULAR MOTION |
| MODERN PUBLICATION | Multiple Choice Questions(LEVEL I) |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
Torque produced by the centripetal force `vecF_(c)`, in circle of radius `vecr` is given by
View SolutionA body of mass m is moving in a horizontal circle of radius 'r. If the centripetal force is F. the kinetic energy of the body is :
View SolutionIn the last problem the linear momentum of the body is:
View SolutionA body of mass m is moving with uniform speed in a horizontal circle of radius r under a centripetal force `(k)/(r^(2))`, where k is a constant. The K.E. of body is :
View SolutionA body of mass m tied to a string of length r is at its lowest position. What should be the minimum speed given to it so as just to complete one revolution ?
View SolutionA body is to be slided without friction along an inclined plane of height 'h' so that it loops the loop of radius at the bottom. The value of height is :
View SolutionA simple pendulum has a length 1. What minimum velocity should be imparted to its bob at the mean position so that the bob reaches a height equal to 1 above the point of suspension ?
View SolutionIn the above problem, what should be the minimum velocity imparted to the bob so that it rises up to a height equal to the length and is parallel to the point of suspension ?
View SolutionA cyclist moves round a circular road of radius 50 metres. If the coefficient of friction between the tyres and road is 0.2, the maximum velocity with which he can go round without skidding is (g = `10 ms^(-2)`:
View SolutionA motor cyclist moves round a curve at a certain speed. He doubles his speed. The ratio of the tangents of the angles by which he leans with vertical in two cases is :
View SolutionA man going on a cycle round a circular track of length 34.3 metres completes one round in `sqrt(22 )`sec. The angle through which he leans inward is :
View SolutionAn iron ball is moving from rim to rim via lowest point at the bottom of a small hemispherical bowl of radius 10 cm. The velocity with which the ball passes from the lowest position is : (g = `9.8 ms^(-2)`)
View SolutionA car is moving on a curved bridge of radius r with velocity v. The maximum velocity with which it can move round it without leaving the bridge at the highest point is :
View SolutionA ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving on a horizontal circle. The string breaks under a tension of 25 N. What is the maximum speed with which the ball can be moved ?
View SolutionFor a car moving along circular road of radius r and with coefficient of friction u between the tyres and the road, the maximum velocity without skidding is :
View SolutionA scooterist is moving round a circular track of radius 480 m. The track is 1 m wide. If his speed is 72 km/hour, how much the outer edge of track is lifted to bank the track for him ? (g = `10 ms^(-2)` )
View SolutionA small body of mass m slides down a hemispherical smooth bowl from the rim to the bottom. The velocity of the body at the bottom is :
View SolutionA particle of mass m is rotating by means of a string in a vertical circle. The difference in the tensions at the bottom and the top would be :
View SolutionA can filled with water is revolved in vertical circle of radius 4 m and water just does not fall down at the highest point. The time period of revolution is (g = 9.87 `ms^(-2)`):
View SolutionA disc revolves in a horizontal plane at the rate of 210 r.p.m. A coin placed at a distance of 2 cm from the axis of rotation just remains at rest on the disc. The coefficient of friction between the dice and coin is (g = `10ms^(-2)`):
View SolutionThe string of a simple pendulum is horizontal at a height and is released. The tension in the string at the lowest point is:
View SolutionA motor car is travelling at 30 ms on a circular curve of radius 500 m. It is increasing its speed at the rate of 2 `ms^(-2)`, what is its acceleration ?
View SolutionA curved road of 50 m radius is banked to a correct angle for the given speed. If the speed is to be doubled, keeping the banking angle to be the same, the radius of curvature of the road should be changed to :
View SolutionA phonograph record on the turn table rotates at 30 r.p.m. The linear speed of a point on the record at the needle 14 cm from the centre is :
View SolutionA railway carriage has its C.G. at a height of 1 m above the rails which are 1 m apart. The maximum speed with which it goes round the track (unbanked) of 250 m radius is: (8 = 10 `ms^(-2)`
View SolutionA particle is attached to one end of a string and is whirled in a horizontal circle with constant angular velocity. Its angular momentum about the centre of its path is 'L'. If the same mass is whirled with same angular velocity but with the length of string halved, the new angular momentum will be:
View SolutionA particle of mass m slides from rest from the top position A of a circular track of radius R. The vertical distance AB travelled by m before leaving the surface at C is :

View SolutionThe kinetic energy `E_(k)` of a particle moving along circle of radius R depends upon the distance x covered and varies as `E_(k)=ax^(2)`. The radial force acting on the particle is :
View SolutionA particle performs uniform circular motion with angular momentum 'L'. If the frequency of revolution is doubled and its kinetic energy is halved, the angular momentum would become :
View SolutionKeeping the banking angle to be the same, if maximum speed with which the vehicle can travel on the curved road is increased by 10%, what should be the increase in the radius of curvature of the curve from 20 m ?
View SolutionA stone of mass 1 kg tied to a light string of length `L=(10)/(3)`m, is whirled in a vertical circle of radius L. If the ratio of maximum to minimum tensions is 4, the speed of the stone at the highest point of the circle is:
View SolutionA stone of mass 1 kg tied to a light string of length `L=(10)/(3)`m, is whirled in a vertical circle of radius L. If the ratio of maximum to minimum tensions is 4, the speed of the stone at the highest point of the circle is:
View SolutionThe slope of the smooth banked road is p. If the radius of the curve is 'r', the maximum velocity with which a car can negotiate the curve is:
View SolutionA tube of length L is filled completely hy an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of the ends with a uniform angular velocity 0. The force exerted by the liquid at the other end is :
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point its :
View SolutionA particle goes round a circular path with uniform velocity v. After describing half the circle, the average acceleration of the particle (if its radius is r) is :
View SolutionA body is describing a circle of radius 'r'. If the centripetal acceleration varies inversely with the square of the radius 'Y', how does its velocity vary with the radius?
View SolutionTwo discs have their planes perpendicular to each other. They are rotating about their axis with angular speeds of 8 rad `s^(-)` and 6 rad `s^(-)` respectively. What is the resultant angular speed ?
View SolutionTwo rigid bodies are rotating with same angular speed co but in opposite directions about common axis. What is the resultant angular speed ?
View SolutionA disc, initially at rest starts rotating with uniform acceleration. During first five seconds it describes an angle Band during next five seconds the angle described is `lambda`. What is`(lambda)/(beta)`?
View SolutionA pendulum of mass 'm' and length l' is suspended to a point. It is displaced and released from a height equal to half the length of the pendulum. The tension in the string at the lowest point is:
View SolutionA particle of mass m describe a circle of radius r. The centripetal acceleration of the particle is`(4)/(r^(2))` What is the momentum of the particle ?
View SolutionThe K.E. of the particle in the above problem will be:
View SolutionA particle is projected into a vertical circular orbit of radius 1 m. In order that it may just rise to the top without the string becoming slack, the velocity of its projection is (g = 10 `ms^(-2)`):
View SolutionTwo particles of equal masses are revolving in circular paths of radii `r_(1)` and `r_(2)` respectively with the same period. The ratio of the centripetal force experienced by the two is:
View SolutionThe ratio of angular speeds of minute-hand and hour hand of a watch is :
View SolutionIf the over-bridge is concave instead of being convex, the thrust on the road at the deepest position by a body of mass m moving with velocity v round the bridge is :
View SolutionThe maximum frictional force between the tyres of a car and the road is half of the weight of the car. If the car negotiates a curve of radius 20 m, the velocity of the car is (g = 10 m`s^(-1)` ):
View SolutionA particle is projected so as to just move along the vertical circle of radius r. The ratio of the tensions in the string, when the particle is at the lowest and highest point on the circle, is :
View SolutionThe length of second's hand in a watch is 1 cm. The change in velocity of its tip in 15 seconds is :
View SolutionA car is moving in a circular horizontal track of radius 10 m`s^(-1)` with a constant speed of 10 ms. A plumb-bob is suspended from the roof of car by a light rigid rod of length 1 m. The angle made by the rod with the track is (8 = 10 `ms^(-2)`):
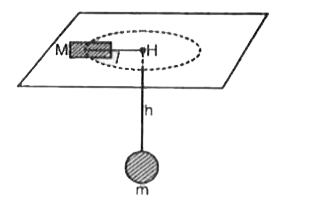
View SolutionA block of mass M is situated on a smooth horizontal frictionless table. A thread tied to the block passes through hole H in the table and carries a mass m at its other end. If the length of thread above the table is 'l'. what should be the value of m so that it remains suspended at a constant height 'h' below the table when M is revolving in horizontal circle with angular speed co on the table ?
View SolutionA particle P is moving with uniform speed of 10 m s in a circle of radius 100 m. C is the centre of the circle and AP its diameter. The angular speed of P about the points A and C are in the ratio of:
View SolutionA mass of 2 kg is tied to a string of length 1 m and is whirled in a vertical circle with a constant speed of 5 m`s^(-1)`. At which location the tension is 70 N ? (8 = 10 m`s^(-2)` )
View SolutionA stone attached to a rope of length 1 = 80 cm is rotated with a speed of 240 r.p.m. At the moment when the velocity is directed vertically upwards, the rope breaks. To what height does the stone rise further?
View SolutionA mass m attached to a string of length 'l' is suspended from the ceiling and is set into motion in a horizontal circle of radius 'r and the string making an angle with the vertical. If `T_(b)`, is the breaking tension of the string the maximum value of ris :
View SolutionA toy-car travels in a horizontal circle of radius 2a', kept on the track by radial clastic string of unstretched length 'a'. The period of rotation is T, The toy-car is speeded up until it is moving in a circle of radius, 3a. Assuming that the string obeys Hooke's law, the period of rotation T now is :
View SolutionThe rotation of a rigid body is defined by the equation`theta=2.5"sin"(pit)/(4)` . The angular velocity of the body for t=2 s will be
View SolutionThe maximum tension which an inextensible ring of mass 0.1 kg/m can bear is 10 N. The maximum velocity in m`s^(-1)` with which it can be rotated is :
View SolutionA stone is rotated steadily in a horizontal circle with a period T by a string of length 2 If the tension in the string is kept constant and is increased by 1%, what is the percentage change in the time period ?
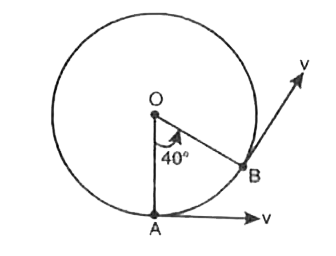
View SolutionA particle moving in a circle of radius 'r' centred at with a constant speed y, the change in velocity in moving from A to B, when angle subtended by it is `40^(@)` is given by :
View SolutionA playing record is revolving at the rate of `33(1)/(3)` rev./min and has a radius 25 cm. A coin of mass m is placed at a distance 20 cm from the centre. What should be the coefficient of friction between coin and record so that the coin just flies off ?
View SolutionA string of length is fixed at one end and carries a mass M at the other end. The string makes .`(2)/(pi)`p.s. about a vertical axis through the fixed end. The angle which the string subtends with vertical is:
View SolutionA mass of 2 kg is whirled in a horizontal circle at an initial speed of 51.p.m. Keeping the radius constant the tension in the string is doubled. The new speed is nearly
View SolutionA particle is moving along a circular path with angular speed co about the axis passing through its centre. What will be its angular speed about a point on the other end of the diameter through the instantaneous position of the particle?
View SolutionA simple pendulum of length 7" with a heavy bob is made to describe a horizontal circle of radius `sqrt((3l)/(2)) `131 What is the time period of revolution of the pendulum?
View SolutionThe K.E. of a particle moving in a circle of radius ris given by `K =betax^(2)`, where x is the distance covered. The force acting on the particle is given by :
View SolutionA swing is at 1 m height above the ground level in its lowermost position and 3m in middle position. Its speed at lowest position is :
View SolutionAngular displacement`(theta)` of a flywheel varies with time as `theta=at bt^(2)-ct^(2)`, then angular acceleration is given by:
View SolutionA meter scale is standing vertically on the earth's surface on one of its end. It now falls on earth without slipping. Find the velocity with which the free end of the scale strikes the earth. (g=9.8 `m//s^(2)`)
View SolutionTwo particles having mass M and I are moving in a circular path having radius R and r. If their time periods are same then the ratio of angular velocity will be:
View SolutionA cyclist riding the bicycle at a speed of `14sqrt3ms^(-1)` takes a turn around a circular road of radius `20sqrt3` m without skidding. Given 8 = 9.8 ms, what is his inclination to the vertical?
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes `(2)/(pi)`revolution per second around the vertical axis through the fixed end as shown in the figure, the tension in the string is :
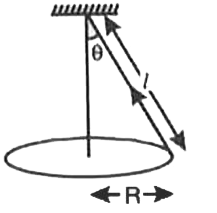
View SolutionThe centripetal force for a car moving on a road is given by:
View SolutionThe minimum velocity (in `ms^(-1)`) with which a car driver must traverse a flat curve of radius 150 m and coefficient of friction 0.6 to avoid skidding is :
View SolutionWhich of the following statements is false for a particle moving in a circle with a constant angular speed ?
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle, the motion of the particle takes place in a plane. It follows that
View SolutionA particle is moving eastwards with a velocity of 5 `ms^(-1)` In 10 seconds the velocity changes to 5 `ms^(-1)` northwards. The average acceleration in this time is :
View SolutionTwo cars of masses `m_(1)` and `m_(2)` are moving in circles of radii `r_(1)`and `r_(2)`, respectively. Their speeds are such that they make complete circles in the same time. The ratio of their centripetal acceleration is :
View Solution
Multiple Choice Questions(LEVEL I) questions and complete solutions for chapter UNIFORM CIRCULAR MOTION of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12