Complete Solutions to Revision Exercises (Short Answer Questions ) of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| MODERN PUBLICATION | Revision Exercises (Short Answer Questions ) |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Derive the force exerted by a magnetic field on a moving charged particle.
View SolutionA charged particle moving with a uniform velocity `vecv` enters a region where uniform electric and magnetic fields `vecE` and `vecB` are present. It passes through the region without any change in its velocity. What can we conclude about the (i) relative direction of `vecE`, `vecV` and `vecB`? (ii) magnetic of `vecE` and `vecB`?
or
Find the condition under which the charged particle moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speeds.
View SolutionDerive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (i) maximum (ii) minimum value.
View SolutionWrite the relation for the force `vecF` acting on a charge carrier q moving with a velocity `vec v` through a magnetic field `vec B` in vector notation. Using this relation, deduce the conditions under which this force will be
(i) maximum (ii) minimum. Under what condition will it move in (i) a circular path and (ii) a helical path?
View SolutionA charged particle q is moving in the presence of a magnetic field B which is inclined to an angle 30° with the direction of the motion of the particle. Draw the trajectory followed by the particle in the presence of the field and explain how the particle describes this path.
View SolutionState the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View SolutionA fine pencil of `beta`-particles, moving with a speed v, enters a region (region I), where a uniform electric field and a uniform magnetic field are both present. These `beta`-particles then move into region II where only the magnetic field, (out of the two fields present in region I) exists. The path of the `beta`-particles, in the two regions is as shown in the figure.
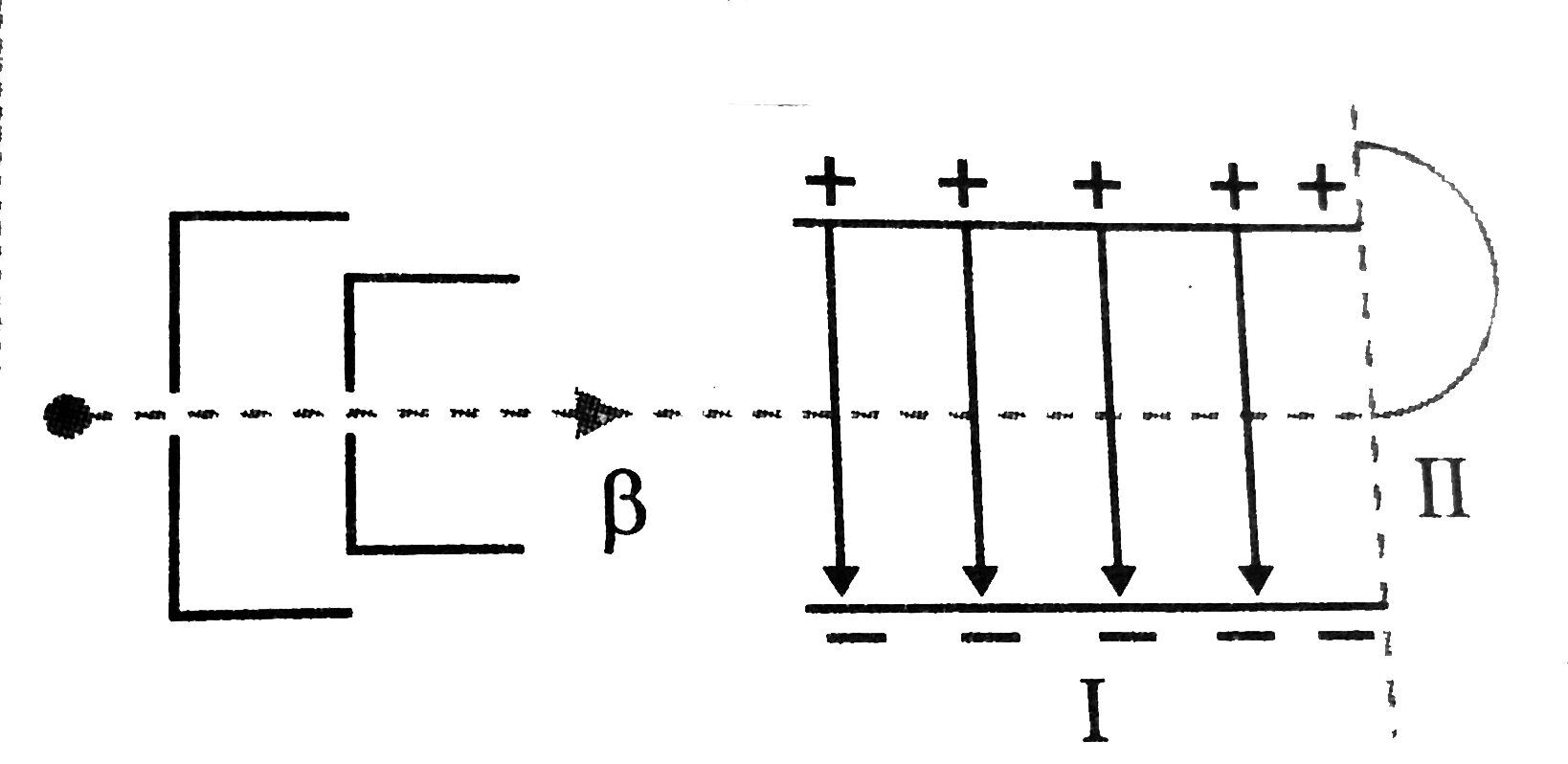
(i) state the direction of magnetic field.
(ii) state the relation between E and B in region I.
(iii) Drive the expression for the radius of the circular path of the `beta`-particle in region II.
(iv) If the magnitude of magnetic field, in region II is changed to n times its earlier value, (without changing the magnetic field in region I) find the factor by which the radius of this circular path would change.
View SolutionTwo parallel wires carrying current in the same direction attract each other while two beams of electrons travelling in the same direction repel each other. Why?
View SolutionExplain the principle and working of a cyclotron with the help of a schematic diagram. Write the expression for cyclotron frequency.
View SolutionA cyclotron is not suitable to accelerate electrons. Why?
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionA current I flows in a conductor placed perpendicular to the plate of the paper. Indicate the direction of the magnetic field due to a small element `dvecl` at point P situated at a distance `vecr` from the element as shown in the figure.
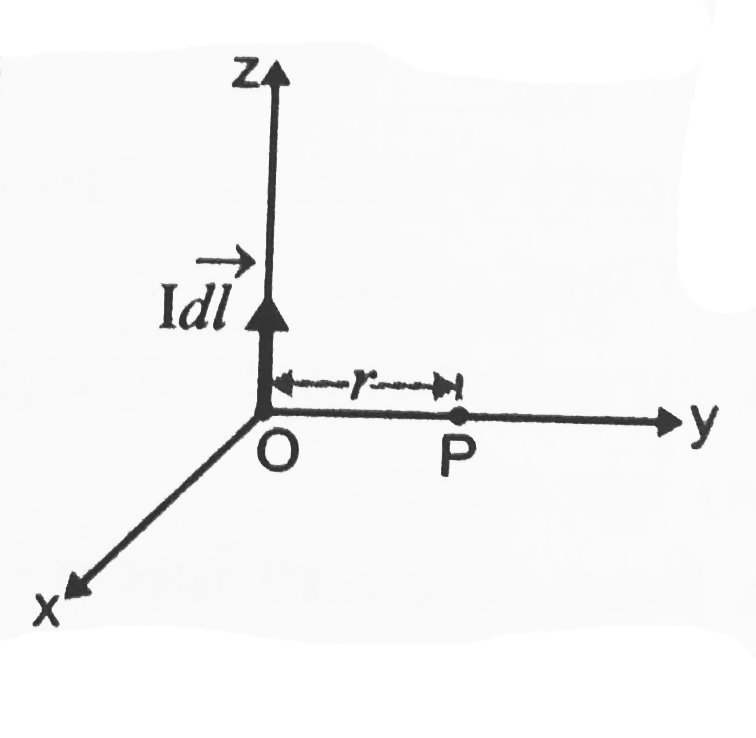
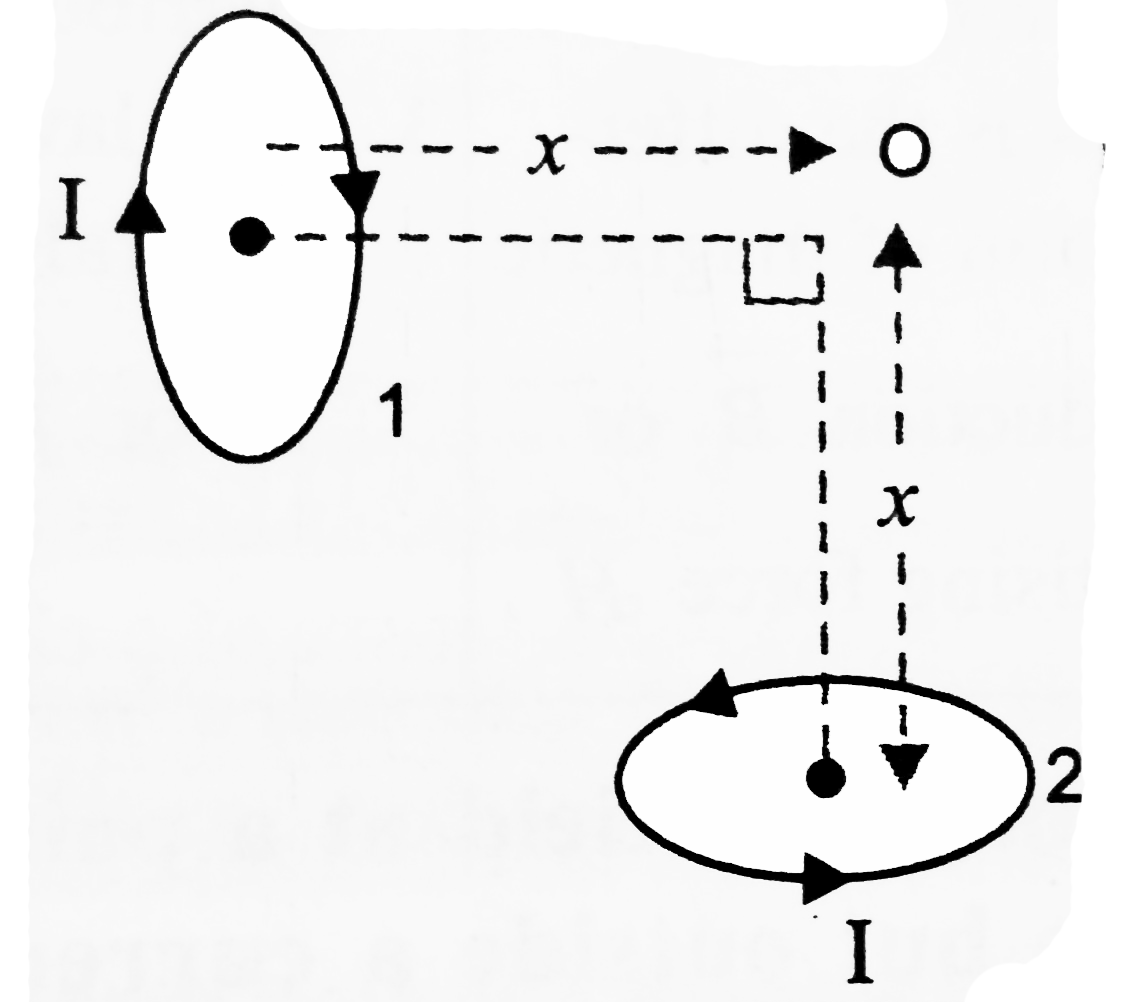
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
View SolutionA wire of length L is bent around in the form of a coil having N turns of same radius . If a steady current I flows through it in a clockwise direction, find the magnitude and direction of the magnetic field produced at its centre.
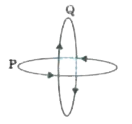
View SolutionTwo identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land `sqrt3 I` respectively.
View SolutionA rectangular coil of sides `l` and `b` carrying a current I is subjected to a uniform magnetic field `vec B` acting perpendicular to its plane. Obtain the expression for the torque acting on it.
View SolutionDefine electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
View SolutionIncreasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity. Justify this statement.
View SolutionWhat is the function of the radial magnetic field in the moving coil galvanometer?
View SolutionTwo protons P and Q moving with the same speed enter magnetic field `B_(1)andB_(2)` respectively at right angles to the field directions. If `B_(2)` is greater than `B_(1)` for which of the protons P and Q the circular path in the magnetic field will have a smaller radius?
View Solution(a) How does a voltmeter differ from ammeter?
(b) What is the main function of soft iron core used in a moving coil galvanometer?
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View Solution(a) State the principle of working of a galvanometer.
(b) Agalvanometer of resistance G is converted into a voltmeter to measure up to V volts by connecting a resistance `R_(1)` , in series with the coil. If a resistance `R_(2)` is connected in series with it, then it can measure up to V/2 volts. Find the resistance, in terms of `R_(1)" and R_(2)`, required to be connected to convert it into a voltmeter that can read up to 2 V. Also find the resistance G of the galvanometer in terms of `R_(1)" and " R_(2)`.
View SolutionA galvanometer of resistance G can be converted into a voltmeter of range `theta-V` volts by connecting a resistance R in series with it. How much resistance will be required to change its range from 0 to `V//2`?
View SolutionA electron of mass, `m_(e)` revolves around a nucleus of charge `+Ze`. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as `vec(mu) = - (e )/(2m_(e)) vec(L)`, where `vec(L)` is the orbital angular momentum of the electron. Give the signification of negative sign.
View SolutionA straight wire of`1.4` m long carries a current of 7 A at right angles to a uniform magnetic field of `0.01` T. Calculate the mechanical force acting on the wire due to the magnetic field.
View SolutionA wire of length l is bent in the form of a square and carries a current I. What is the value of its magnetic moment?
View SolutionState the factors on which the current sensitivity of a galvanometer is increased.
View Solution
Revision Exercises (Short Answer Questions ) questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- CHAPTER PRACTICE TEST
- COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (ASSERTION TYPE QUESTIONS)
- COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (INTEGER TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT (Exemplar Problems ) (Short Answer Type Questions )
- NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
- NCERT FILE (NCERT Additional Exercises)
- NCERT FILE (NCERT Textbook Exercises)
- PRACTICE PROBLEMS
- Revision Exercises (Additional Questions )
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer Questions )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer Questions )
- Revision Exercises (Very Short Answer Questions )
- SOLVED EXAMPLES
- Tough & Tricky (PROBLEMS )