Complete Solutions to PRACTICE PROBLEMS of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| MODERN PUBLICATION | PRACTICE PROBLEMS |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
In a region of magnetic field 0.05 T directed along positive direction of Y-axis, a beam of charged particles enters the region along X-axis with a velocity of `2.5 xx 10^(4) m s^(-1)`. Calculate the radius of circular path described by the charge particles if their charge to mass ratio is `7.5 xx 10^(6) C kg^(-1)`.
View SolutionThree charged particle with charge in ratio,` 1:1:2` and mass in ratio `1 : 2:4` enters in a region of uniform magnetic field. Calculate the ratio of radii of circular path described by three particles when inetic energy of all three particles is same.
View SolutionA long conducting wire is placed along Y-axis and a current of 5 A is flowing through it in positive Y-axis. A charged particle of charge ` + 3.2 xx 10^(-19)` C is moving parallel to the conductor towards negative Y-axis with a speed of `5 xx 10^(4) m s^(-1)`. Calculate the force exerted by the magnetic field of current on charged particle. The perpendicular distance between charged particle and wire is 25 cm.
View SolutionCan we calculate the force experienced by a charge moving in a magnetic field?
View SolutionA cyclotron's oscillator frequency is `10MHz`. What should be the operating magnetic field fro accelerating protons? If the radius of its dees is `60cm`, what is the kinetic energy (in `MeV`) of the proton beam produced by the acceleration?
`(e-1.60xx10^-19C,m_p=1.67xx10^-27kg, 1MeV=1.6xx10^-13J)`
View SolutionA beam of charged particle enters in a region of magnetic field of `5 xx 10^(-3)` weber m and electric field of `2.5 xx 10^(4) Vm^(1)`,acting perpendicularly. Calculate the speed of particles perpendicular to electric and ,magnetic field , if their path remains unchanged. The given charge on particles and mass are ` 3.2 xx 10^(-19) C " and " 12 xx 10^(-31) ` kg , respectively.
View SolutionA beam of charged particle enters in a region of magnetic field of 5 × 10^(−3) weber m and electric field of 2.5 × 10 4 V m 1 ,acting perpendicularly. Calculate the speed of particles perpendicular to electric and ,magnetic field , if their path remains unchanged. The given charge on particles and mass are 3.2 × 10 − 19 C and 12 × 10 − 31 kg , respectively.calculate the radius of circular path traced by the charged particle if the electric field is removed .
View SolutionA proton is accelerated in cyclotron with dees of radius 40 cm has a operating frequency of 12 MHz. Calculate the magnitude of magnetic field. Given mass of proton, `m_(P) = 1.67 xx 10^(-27) ` kg and charge on proton ` q_(P) = 1.6 xx 10^(-19) C`.
View SolutionAn alpha particle is accelerated in a cyclotron with dees of radius 40 em and operating at frequency of 20 MHz. Calculate the kinetic energy of the alpha particle if magnetic field in cyclotron ia 1 tesla.
Given, mass of alpha particle `m_(alpha) = 6.65 xx 10^(-27) `kg and charge of `alpha` - particle `q_(alpha) = 3.2 xx 10^(-19) C`.
View SolutionA wire of length 15 cm carrying current of 5 Ais balanced in air by a uniform magnetic field, B. The mass of wire is` 0.5` grams.
Calculate the value of B.
Use g = `10 ms^(-2)`.
View SolutionAn iron rod of mass 50 g and length 50 cm is suspended by master wires as shown in the figure. Calculate the magnitude and direction of magnetic field to be set in the region such that the tension is the wires is zero. The current in the rod is 4 A.

View SolutionA square loop of conducting wire of side 10 cm carrying current of 1 A shown in adjoining figure is placed in a region of magnetic field of` 0.2` T directed towards positive X-axis calculate the force on each side of the square.
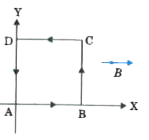
View Solutionचुम्बकीय क्षेत्र में गतिमान आवेश पर लगने वाले बल की दिशा ज्ञात होती हैं-
View SolutionCalculate the maximum torque experienced by a rectangular coil of length 10 em and breadth 8 cm carrying current of 100 mA and has 1,000 turns placed in a region of magnetic field of `0.2 T` such that magnetic field lie on the plane of coil.
View SolutionA coil bent in form of an equilateral triangle of side 10 cm is suspended with the help of a mass less string through one of its vertex. Calculate the torque experienced by the coil if the magnetic field in the region is` 0.2` T directed horizontally and current of 1 A is passing through the coil.
View SolutionA wire is bent to form a circular coil of radius 5 cm with 20 loops. The coil is placed in a magnetic field of `0.5` T and a current of 1 A flow through it. Calculate the maximum torque exerted by magnetic field.
View SolutionA rectangular coil of 10 em by 8 cm is suspended vertically in a region of horizontal magnetic field of `1.5 `T such that the field lines make an angle of `60^(@)` with the normal to the coil. Calculate the couple acting on the coil when a current of 5 A is passing through it.
View SolutionA circular coil of 30 turns and radius 15 cm carries a current of 5 A. Calculate the net torque on the coil when it is placed in a uniform magnetic field of` 0.2` T normal to the plane of coil. Also calculate the net force on the coil.
View SolutionA circular coil of 30 turns and radius 15 cm carries a current of 5 A. placed in a uniform magnetic field of 0.2 T normal to the plane of coil. , the coil has an aren of cross section `2 xx 10^(-6)m^(2)` and electron density of `10^(27) m^(-3)` . Calculate the average force on each electron in the coil due to magnetic field.
View SolutionA rectangular loop of length 10 cm and 8 cm is carrying current of 10 A placed in X-Y plane as shown in adjoining figure. Calculate the torque on the loop if uniform magnetic field of` 0.2` T is directed along positive Z-direction.
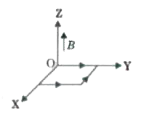
View SolutionA coil having 1,000 turns closely wound and an area of cross section `2 xx 10^(-5) m^(2)` carries a current of 4A. The coil is kept in a region of uniform magnetic field of` 0.2` T. Calculate the net torque acting on the coil if it is free to move about vertical axis and its axis makes an angle of `30^(@)` with the magnetic field lines.
View SolutionThe rectangular coil of a moving coil galvanometer has area of `8 xx 10^(-4) m^(2)` and 100 turns. The coil is kept in a radial horizontal magnetic field of` 0.2` T.
Calculate the restoring torque constant of hair spring connected to coil when current of `4 xx 10^(-5)` A passes through it and deflects the scale by `20^(@)` .
View SolutionA moving coil galvanometer has a rectangular coil of area `10^(-3) m^(2) ` and 150 turns. The torsional constant of the hair springe connected to the coil is `5 xx 10^(-7)` Nm per degree. The maximum angular deflection is `30^(@)` .
Calculate the maximum current that can be measured by it if its rectangular coil is kept in a radial horizontal magnetic field of `2,000 G` .
View SolutionIn previous problem, if the minimum angular deflection that can be recorded is `0.2^(@)`, then calculate the minimum current that can be measured by the galvanometer.
View SolutionIn a moving coil galvanometer, the current sensitivity increases by `30%` .
When the coil resistance is doubled, calculate the percentage change in its voltage sensitivity.
View SolutionTwo moving coil galvanometers A and B have rectangular coil of 100 turns each. The area of coil of galvanometers A and B are `2 xx 10^(-4) m^(2) " and " 6 xx 10^(-4) m^(2)` respectively. Calculate the ratio of current sensitivity of A to B if coils in both salvanometers are kept in a radial horizontal magnetic field of `0.2` T and the torsional constant of hair springs are also same.
View SolutionIn the previous problem calculate the ratio of voltage sensitivity if ratio of resistance of coil A to resistance of coil B is` 1:3`.
View SolutionCalculate the magnetic field at a point P. `0.5 `m away from an infinitely long straight wire carrying current of 90 A.
View SolutionCalculate the magnetic field induction at the centre of a square shaped coil of side 10 cm, if it carries of current of 1A.

View SolutionA point charge `3.2 xx 10^(-19) C " makes " 7 xx 10^(15)` revolutions per second in a circular path of radius `1 Å` . Calculate the magnetic induction at the centre of the circular path.
View SolutionAn electron moves with a uniform speed of `1.8 xx 10^(6) m s^(-1)` in a circular orbit of radius `0.8 Å`. Calculate the magnetic induction at the centre of orbit.
View SolutionConsider a tightly wound 100 turn coil of radius 10 cm, carrying a current of 1 A. What is the magnitude of magnetic field at the centre of the coil?
View SolutionA straight wire carrying a current of 12 A is bent into a semi-circular are of radius of` 2.0` cm as shown in the adjoining figure (a). Consider the magnetic field B at the centre of the arc. Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way a shown in figure (b)?

View SolutionMagnetic field at the centre of a circular loop with n turns is `0.50` mt. Calculate the value of n if current of `5.3` A flows in the loop and radius of loop is 2 cm.
View SolutionA circular coil with 100 turns and radius 20 cm is kept in Y-Z plane with its centre at the origin. Find the magnetic field at point (20 cm, 0, 0) if coil carries a current of` 2.0` A.
View SolutionA` 0.5` m long conducting wire is bent in form of a circle, Calculate the magnetic field at the centre if wire carries a current of 5 A.
View SolutionTwo circular loops of radius 6 cm and 8 cm are kept in Y-Z plane with their centres at (0, 0, 0) and (14 cm, 0, 0). Current in the first loop is 1 A and is in an anticlockwise direction, when seen from the second loop. Calculate the magnitude and direction of current in the second loop such that net magnetic field at point (8 cm, 0, 0) is zero.
View SolutionHow are the magnitude and direction of magnetic field at a point denoted by the magnetic lines of force ?
View SolutionA circular metallic ring has a radius r. A battery of V volts is connected across the diameter of the ring as shown in the adjoining figure. Calculate the magnetic field at the centre of the coil.
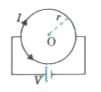
View SolutionA straight conducting wire is bent as shown in the adjoining figure. Calculate the magnetic field at point O.

View SolutionA wire is bent forming two semicircles as shown in the figure. Calculate the magnitude of magnetic intensity at the centre.

View Solution. A small circular ring of radius R is placed in Y-Z plane with its centre at `(-a , 0, 0)`. Another small circular ring of same radius Ris placed in X-Z plane with its centre at` (0, -a , 0)`. Calculate the magnitude and direction of net magnetic field at the origin (0, 0, 0), if both the rings carry current I. The direction of current in the first loop and the second loop is clockwise and anticlockwise respectively, when seen from the origin.
View SolutionCalculate the change in magnetic field induction at the centre of a current carrying loop of radius R, if the radius of coil is reduced to half and current through it changes from I to 2I .
View SolutionDeduce the expression for the magnetic field induction at the centre of a circular electron orbit of radius r, and angular velocity of orbiting electron `omega`.
View SolutionTwo current carrying wire-1 and 2 infinitely long wires are kept parallel at a distance of 5 cm. Calculate the magnitude and direction of force per unit length on each wire if current of 6 A and 12 A flows in first and second wire respectively, in a similar direction.
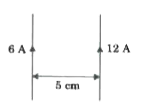
View SolutionA square loop of side 15 cm carrying current of 10 A is kept at a distance of 5 cm from a long wire carrying 12 A current as shown in the adjoining figure. Calculate the net force acting on the loop.
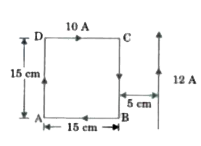
View SolutionTwo wires A and B of length 5 cm and infinite are kept 5 cm apart. Calculate the force experienced by wire B on A if wire A and B carry current of 10 A and 12 A respectively.
View SolutionA straight long wire carrying current 50 A is placed on a horizontal surface. Another wire of unit length carrying 22 A current is balanced in air above at a distance of` 0.5` cm from the long wire. Calculate the mass of the wire.
View SolutionA rectangular loop of wire of size `4 cm xx 10 cm` carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.

View SolutionA solid cylinder carries current of 1 A uniformly distributed over its cross sectional area. Calculate the magnetic field induction at point P, at a distance of 3 cm from the axis of cylinder, if its radius is 7 cm .
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for `(i) r lt a , (ii) r gt a `.
View SolutionA long conducting wire of radius 1 cm carrying current of 1 A placed with its axis coinciding with X-axis. Find the magnetic field at point having coordinates `(0.5 cm, 0.5 cm )` .
View Solutionएक छड़ चुंबक के ध्रुवो के बीच की दूरी 10 cm है । इसके मध्यबिंदु से 15 cm तथा 20 cm पर उसके अक्ष पर स्थित दो बिन्दुओ पर चुंबकीय क्षेत्रो का अनुपात निकाले ।
View SolutionA long conducting wire of radius 5 cm, carrying current of 2 A is placed with its axis coinciding with Y-axis and lies on XZ-plane. Calculate the magnetic field induction at point A (3 cm, 3 cm, 3 cm) and (8 cm, 8 cm, 8 cm) if relative magnetic permeability of conductor is 300.
View SolutionA solenoid of length `0.5` m has a radius of 1 cm and is made up of 500 turns, It carries a current of 5 A. What is the magnitude of magnetic field inside the solenoid?
View SolutionA one metre long solenoid carrying current of 10 A has a radius of 1 cm. Calculate the magnitude of magnetic field inside the solenoid if it has 500 turns per metre.
View SolutionThe magnetic field inside a solenoid is
View SolutionA wire carrying current of 5 A is wound on a toroid in 4,000 turns, Calculate the magnetic field inside the core of toroid and outside the toroid if its inner radius is 15 cm and the outer radius is 18 cm.
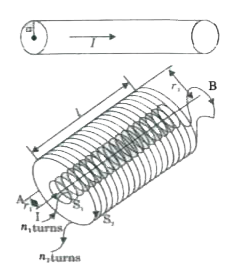
View Solution(a) State Ampere's circuital law, expressing it in the integral form.
(b) Two long coaxial inlsulated soenoids, `S_(1)` and `S_(2)` of equal lengths are would one over the other as shown in the figure. A steady current ''I'' flows through the inner solenoid `S_(1)` to the other end B, which is connected to the outer solenoid `S_(2)` through which the same current ''I'' flows in the opposite direction so as the come out at end A. If `n_(1)` and `n_(2)` are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) inside on the axis and
(ii) outside the combined system.
View Solution
PRACTICE PROBLEMS questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- CHAPTER PRACTICE TEST
- COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (ASSERTION TYPE QUESTIONS)
- COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (INTEGER TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT (Exemplar Problems ) (Short Answer Type Questions )
- NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
- NCERT FILE (NCERT Additional Exercises)
- NCERT FILE (NCERT Textbook Exercises)
- PRACTICE PROBLEMS
- Revision Exercises (Additional Questions )
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer Questions )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer Questions )
- Revision Exercises (Very Short Answer Questions )
- SOLVED EXAMPLES
- Tough & Tricky (PROBLEMS )