Complete Solutions to Tough & Tricky (PROBLEMS ) of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| MODERN PUBLICATION | Tough & Tricky (PROBLEMS ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
A flat disc of radius R charged uniformly on its surface at a surface charge density `sigma`. About its central axis of rotation it rotates at an angular speed `omega`. Find the magnetic moment of disc due to rotation of charges.
View SolutionA wire of uniform cross section is used to make the given system. The radius of semicircle BCD is R and that of AFE is 2R while current I enters at point A.
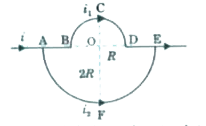
Find the magnetic field intensity at point O in the figure if resistance per unit length of wire is `lambda`.
View SolutionA uniform magnetic field is applied in a circular region of radius R as shown in the given figure. A charged particle of charge q and mass m enters with a velocity from point P along the line that is making an angle with the line segment OP, in the region of magnetic field.
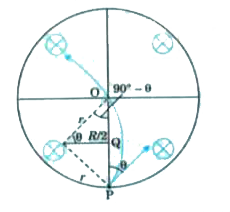
The charged particle is found to pass through the centre of the circular region. Find the angle `theta`.
Given : `B = 1 T, R = 10 cm, m = 6 xx 10^(-3) kg , q = 6 xx 10^(-2) C, v = 1 //sqrt3`.
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA long wire carrying a current `i` is bent to form a plane angle `theta`. The magnetic field at a point on the bisector of this angle situated at a distance `d` forms vertex is
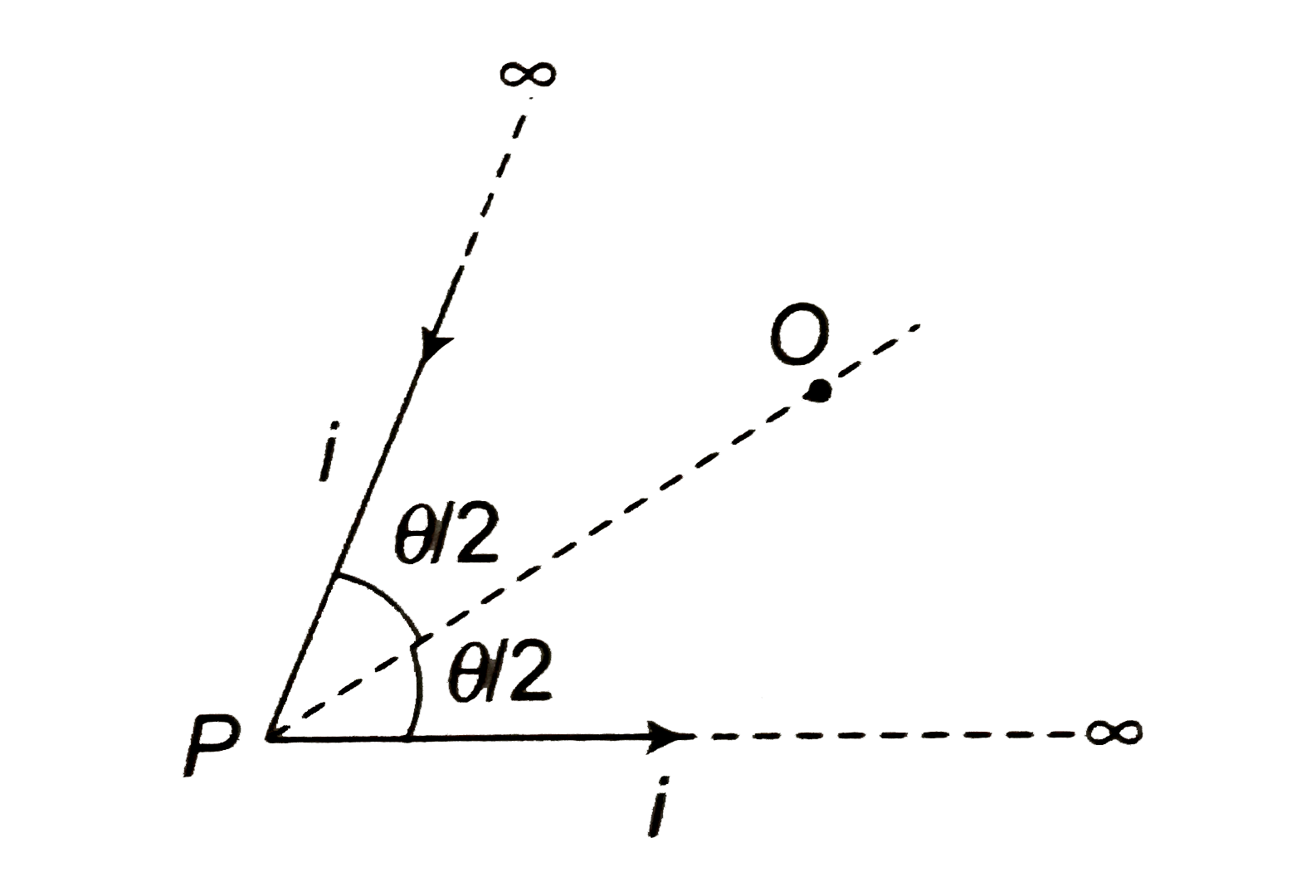
View SolutionA capacitor of capacitance `100 mu F` is connected to a battery of 20 volts for a long time and then disconnected from it. It is now connected across a long solenoid having 4000 turns per meter. It is found that the potential difference across the capacitor drops to `90%` of its maximum value in 2.0 seconds. Estimate the average magnetic field produced at the centre of the solenoid during this period.
View SolutionA circular loop of radius R, carries current. At what distance from the centre of the loop along the axis, the magnetic field intensity becomes half of its magnetic field intensity at the centre. Given: `root(3)(4) = 1.5874 & sqrt(0.5874) = 0.7664`.
View SolutionA uniformly charged ring of radius `R` is rotated about its axis with constant linear speed `v` of each of its particle. The ratio of electric field to magnetic field at a point `P` on the axis of the ring distant `x=R` from centre of ring is `( c` is speed of light )

View SolutionThe path of a charged particle moving in a uniform steady magnetic field cannot be a
View SolutionLet there be one sheet of infinite length and breadth is shown in the figure given below. Electric current is flowing along the length of sheet (perpendicular to the plane of paper). K is the electric current per unit width in this given sheet. Evaluate the magnetic field intensity near this sheet of current.

View SolutionTwo metal sheets of infinite width carrying current K per unit width, as shown in the figure, are kept parallel to each other. The direction of current in both the sheets is opposite to each other. A charged particle q of mass m is projected with a speed u perpendicularly into the plane of paper. What will be the radius of the circular path traversed by the charged particle due to magnetic field of sheets?

View SolutionA long, straight wire carries a current `i`. Let `B_1` be the magnetic field at a point P at a distance d from the wire. Consider a section of length `l` of this wire such that the point P lies on a perpendicular bisector of the section. Let `B_2` be the magnetic field at this point due to this section only. Find the value of d/l so that `B_2` differs from `B_1` by 1 %.
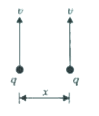
View SolutionTwo equal point charges q are moving parallel to each other with the same speed v as shown in the given figure. These charges can be same visualised as parallel currents in same direction and hence they will apply magnetic attraction on each other. What will be the magnetic force exerted by one on another? At what speed this magnetic force gets balanced by the electric repulsion between them?
View SolutionThere is one long solenoid with turns per unit length. The radius of the solenoid is R and current flowing through it is I. There is a charged particle having charge q and mass m projected from a point on axis of the solenoid, and in a direction perpendicular to the axis. Find the maximum possible speed with which the charged particle can be projected so as not to strike the solenoid.
View SolutionA metallic sphere rotates with angular speed and its surface charge density is o. Find the magnetic field intensity at the centre of sphere. Assume the radius of the sphere to be equal to R.
View Solution
Tough & Tricky (PROBLEMS ) questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- CHAPTER PRACTICE TEST
- COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (ASSERTION TYPE QUESTIONS)
- COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (INTEGER TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT (Exemplar Problems ) (Short Answer Type Questions )
- NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
- NCERT FILE (NCERT Additional Exercises)
- NCERT FILE (NCERT Textbook Exercises)
- PRACTICE PROBLEMS
- Revision Exercises (Additional Questions )
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer Questions )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer Questions )
- Revision Exercises (Very Short Answer Questions )
- SOLVED EXAMPLES
- Tough & Tricky (PROBLEMS )