Complete Solutions to COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS) of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| MODERN PUBLICATION | COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS) |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
A beam of electrons passes underfected throgh unifromly perpendicular electric and magnetic fields. If the electric field is swiched off, and the same magnetic field is maintained the electrons move:
View SolutionA cylindrical conductor of radius `R` is carrying constant current. The plot of the magnitude of the magnetic field, `B` with the distance, `d` from the centre of the conductor , is correctly represented by the figure:
View SolutionThe magnetic force acting on a charged particle of charge `-2 muC` in a magnetic field of `2 T` acting `y` direction, when the particle velocity is `(2i + 3 hat(j)) xx 10^(6) ms^(-1)`, is
View SolutionA thin ring of radius `R` meter has charge `q` coulomb uniformly spread on it. The ring rotates about its axis with a constant frequency of `f` revolution/s. The value of magnetic induction in `Wb m^(-2)` at the centre of the ring is
View SolutionIn mass spectrometer used for measuring the masses of ions, the ions are initaily accerlerated by an electric potential `V` and then made to describe semicircular paths of radius `R` using a magnetic field `B`.if `V` and `B` are kept constant, the ratio `(("charg e on the ion")/("mass of the ion"))` will be propertional to:
View SolutionCurrent sensitivity of a moving coil galvanometer is 5 div/mA and its voltage sensitivity (angular deflection per unit voltage applied) is 20 div/V. The resistance of the galvanometer is
View SolutionA closed loop `PQRS` carrying a current is place in a unifrom magnetic forces on segments `PS, SR` and `RQ` are `F_(1), F_(2)` and `F_(3)` respectively and are in the plane of the paper and along the directions shown, the force on the segment `QP` is
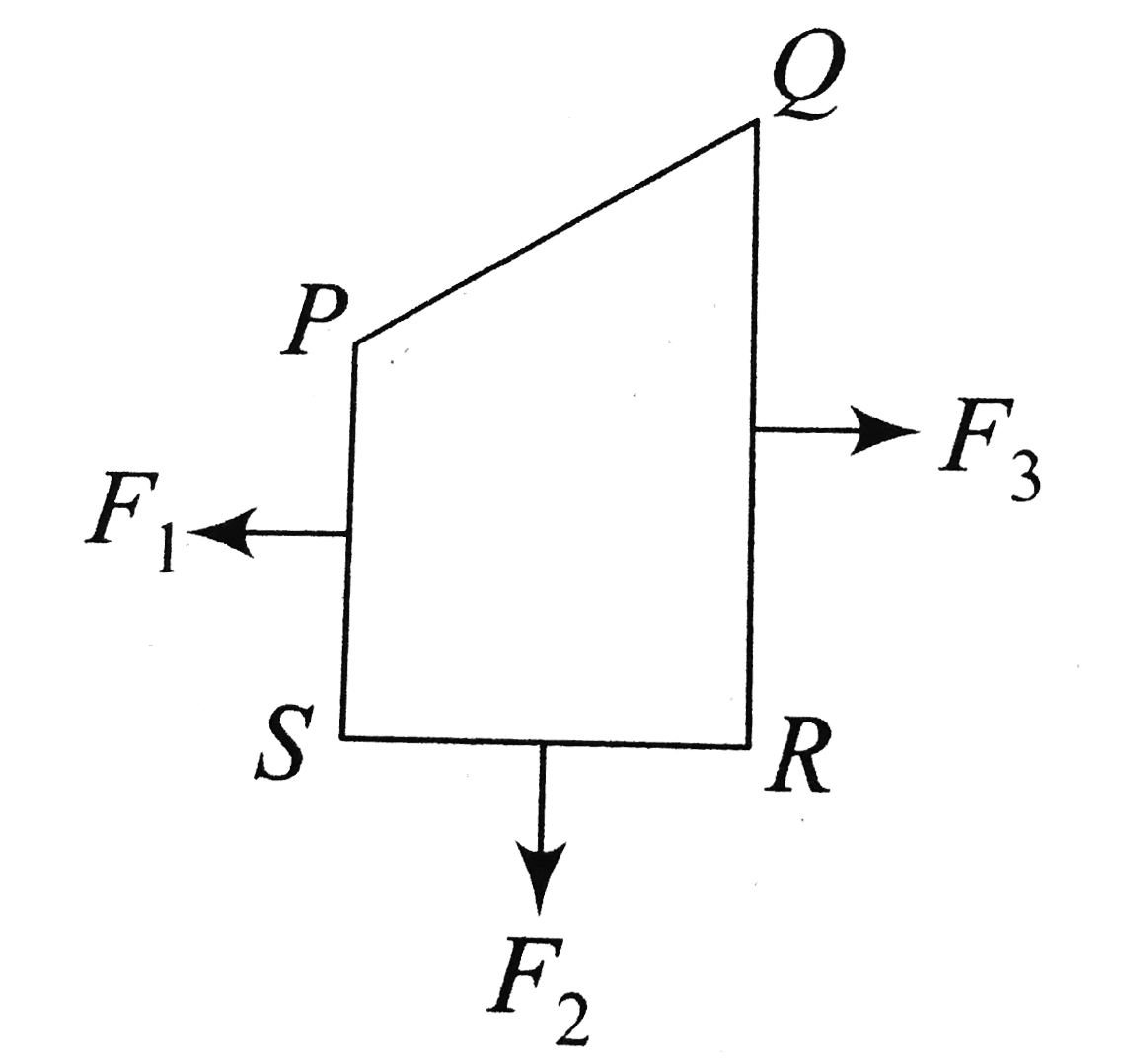
View SolutionA circular disc of radius `0.2 m` is placed in a uniform magnetic fied of induction `(1)/(pi) ((Wb)/(m^(2)))`
in such a way that its axis makes an angle of `60^(@)` with The magnetic flux linked with the disc is
View SolutionA square current carrying loop is suspended in a uniform magnetic field acting in the plane of the loop. If the force on one arm of the loop is `vec(F)`, the net force on the remaining three arms of the loop is
View SolutionA current carrying closed loop in the from of a right angle isoseles triangle `ABC` is placed in a unifrom magnetic fild acting along `AB`. If the magnetic force on the arm `BC` is `F`, the force on the arm `AC` is
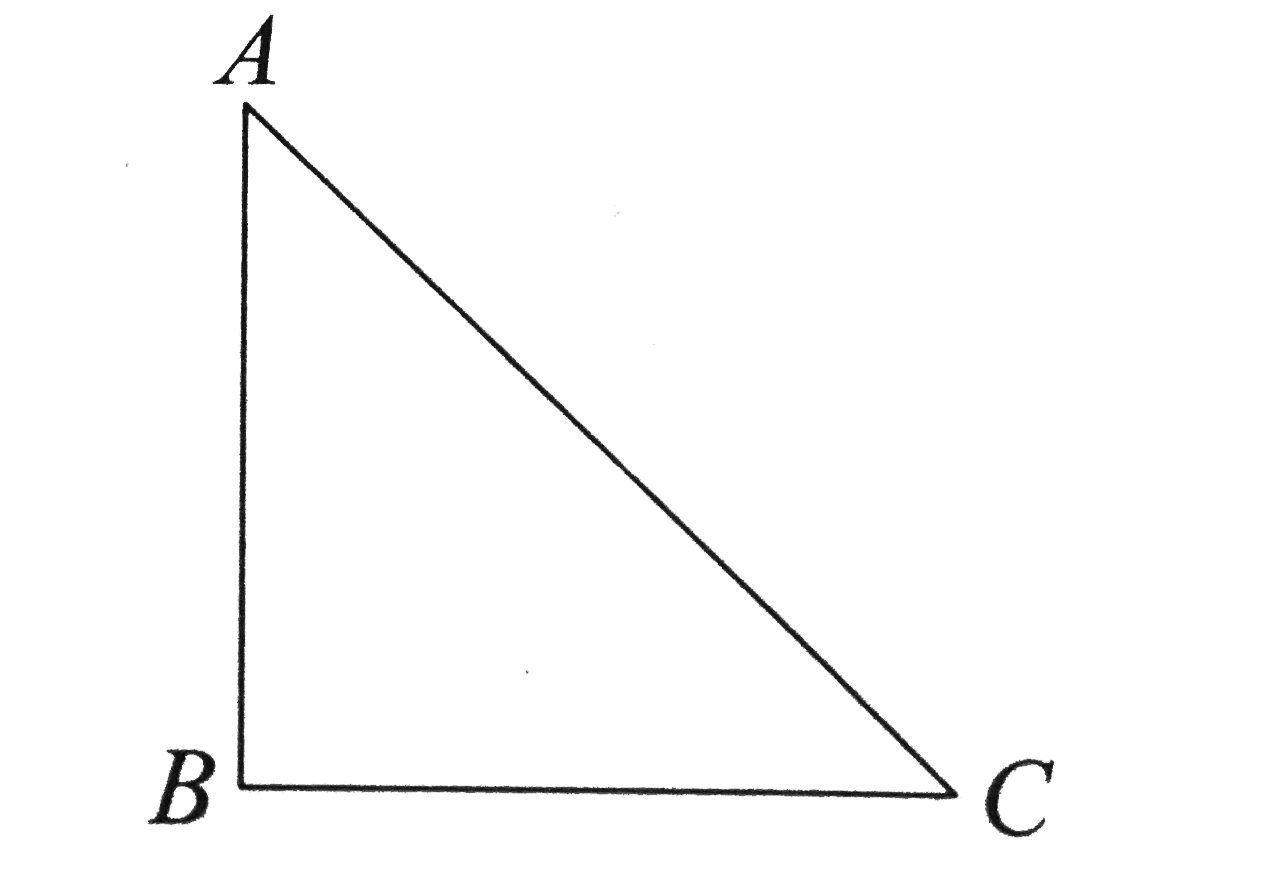
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA bar magnet of lenth `l` and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be

View SolutionA current loop in a magnetic field
View SolutionWhen a proton is released from rest in a room, it starts with an initial acceleration `a_(0)` towards west. When it is projected towards north with a speed `v_(0)` it moves with an initial acceleration `3a_(0)` toward west. The electric and magnetic fields in the room are
View SolutionTwo identical long conducting wires AOB and Cod are placed at right angles to each other, with one above other such that O is their common point for the two. The wires carry `I_(1) and I_(2)` currents, respectively. Points P is lying at distance d form O along a direction perpendicular to the plane containing the wires. The magnetic field at the point P will be
View SolutionAn electron moving in a circular orbit of radius `r` makes `n` rotation per secound. The magnetic field produced at the centre has magnitude
View SolutionA wire carrying current `I` has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius `R` is lying in `Y-Z` plane. Magnetic field at point `O` is
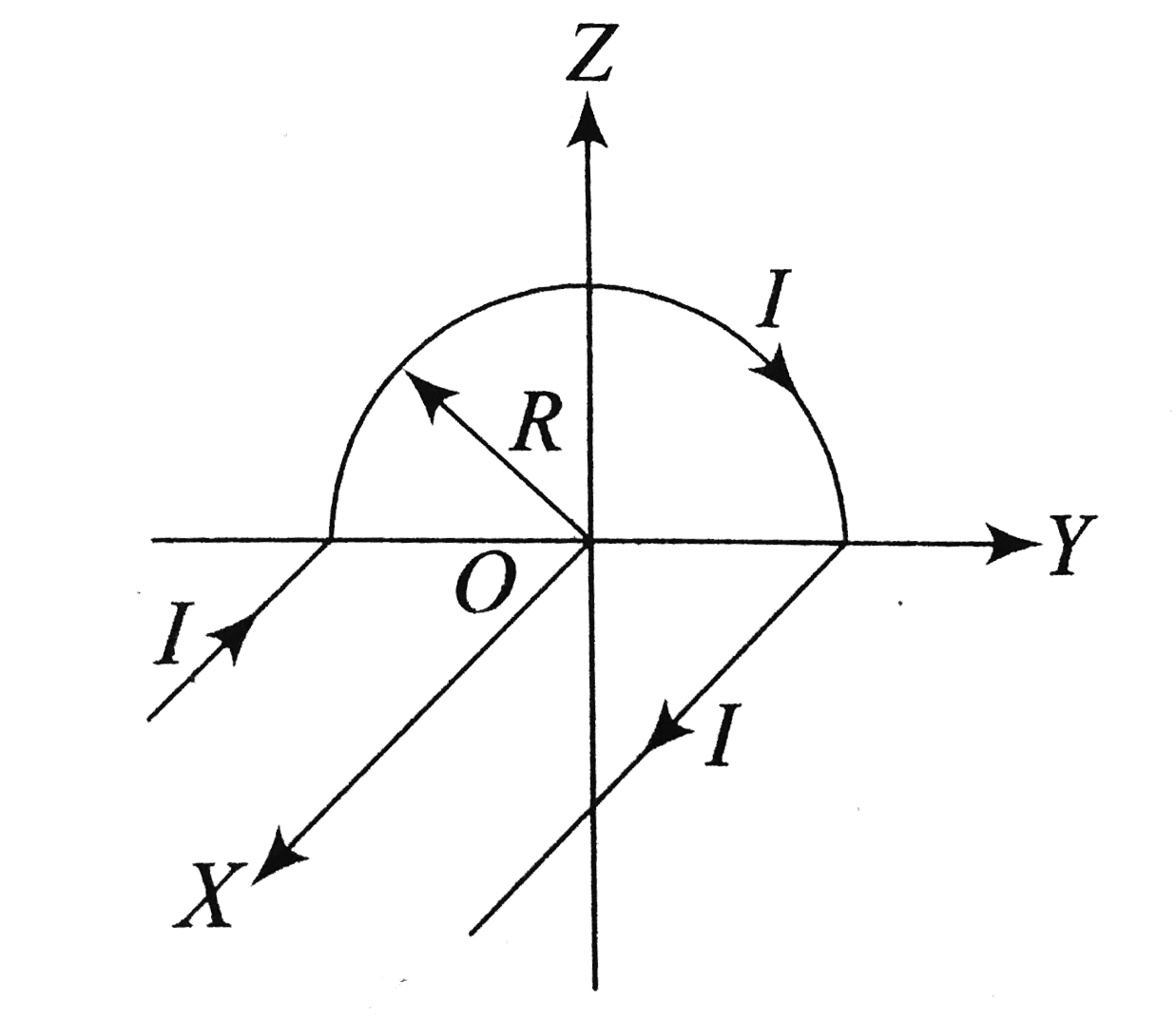
View SolutionA square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
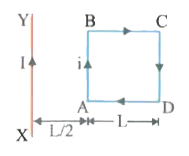
View SolutionA long straight wire of radius `a` carries a steady current `I`. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields `B` and `B'` , at radial distances `(a)/(2)` and `2a` respectively from the axis of the wire is:
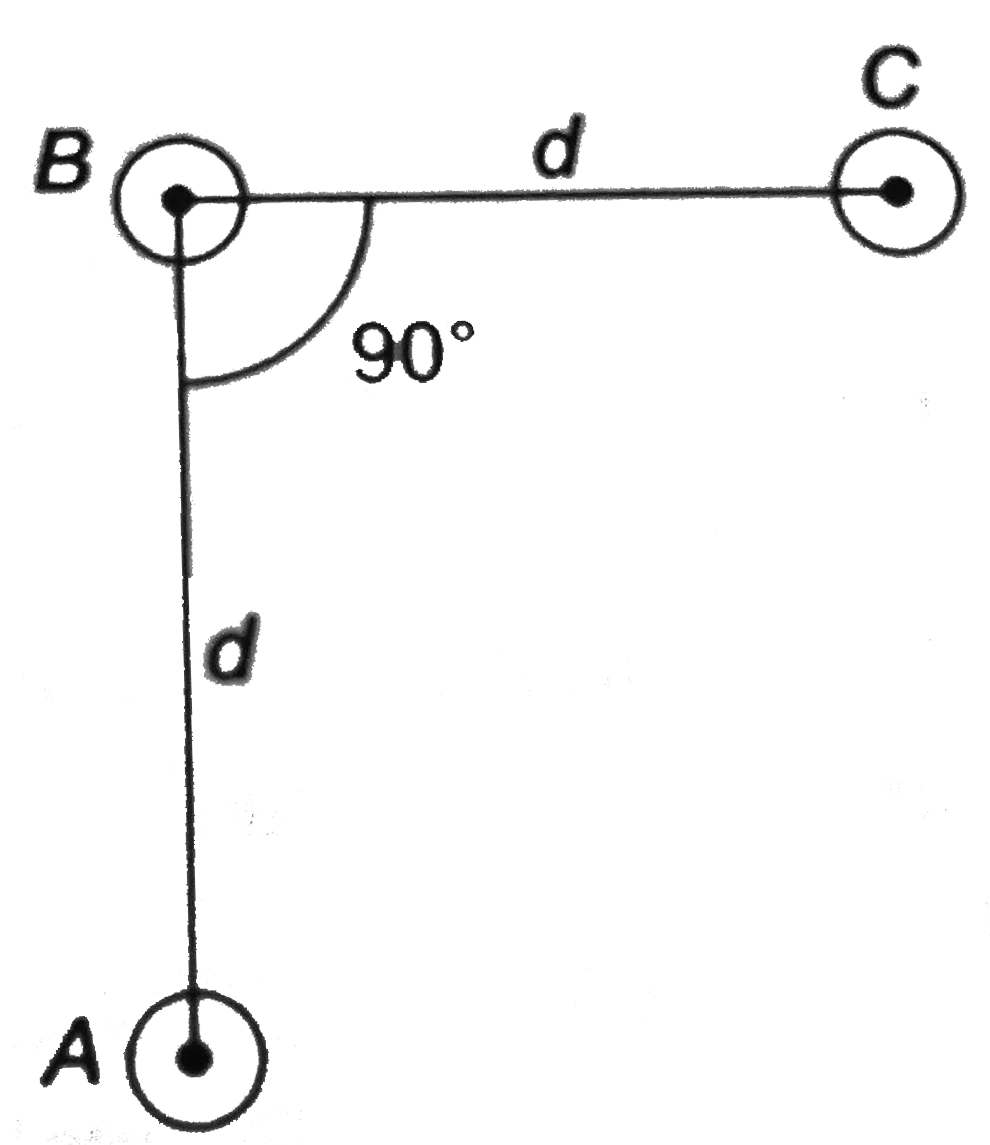
View SolutionAn arrangment of three parallel staright wires placed perpendcular to plane of paper carrying same current `I` along the same direction is shown in figure. Magnitude of force per unit length on the middle wire `'B'` is given by
View SolutionA 250-turns rectangular coil of length 2.1 cm and width 1.25 cm carries a current of `85 muA` and subjected to magnetic field of strength `0.85 T`. Work done for rotating the coil by `180^(@)` against the torque is
View SolutionA charged particle moves through a magnetic field perpendicular to its direction. Then
View SolutionTwo identical conducting wires `AOB and COD` are placed at right angles to each other. The wire `AOB` carries an electric current `I_(1) and COD` carries a current `I_(2)`. The magnetic field on a point lying at a distance `d` from O, in a direction perpendicular to the plane of the wires `AOB and COD`, will be given by
View SolutionTwo very long, straight, and insulated wires are kept at `90^(@)` angle from each other in xy-plane as shown in the figure. These wires carry currents of equal magnitude I, whose directions are shown in the figure. The net magnetic field at point will be:

View SolutionA current I flows along the lenght of an infinetely long, straight, thin walled pipe. Then
View SolutionA horizontal overheadpowerline is at height of `4 m` from the ground and carries a current of `100 A` from east to west. The magnetic field directly below it on the ground is
`( nu_(0) = 4 pi xx 10^(-7) Tm A^(-1)`
View SolutionA current loop `ABCD` is held fixed on the plane of the paper as shown in figure. The arcs `BC( radius = b) and DA ( radius = a)` of the loop are joined by two straight wires `AB and CD` at the origin `O` is 30^(@)`. Another straight thin wire with steady current `I_(1)` flowing out of the plane of the paper is kept at the origin .
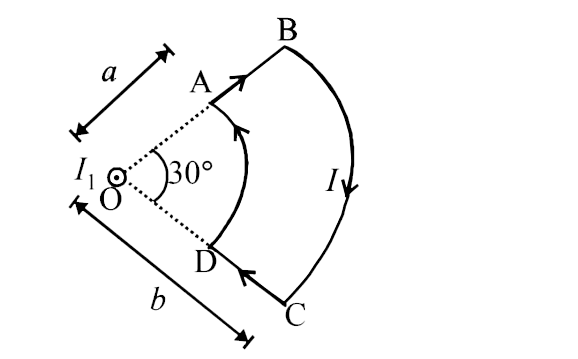
Due to the process of the current `I_(1)` at the origin:
View SolutionTwo long parallel wires are at a distance ` 2d` apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field `B` along the line `XX` is given by
View SolutionAn electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii `r_(e),r_(p),r_(alpha)` respectively in a uniform magnetic field B. The relation between `r_(e),r_(p),r_(alpha)` is:
View SolutionA thin circular disk of radius `R` is uniformly charged with density `sigma gt 0` per unit area.The disk rotates about its axis with a uniform angular speed `omega`.The magnetic moment of the disk is :
View SolutionA current `I` flows an infinitely long wire with cross section in the form of a semi - circular ring of radius `R`. The magnitude of the magnetic induction along its axis is :
View SolutionA charge `Q` is uniformly distributed over the surface of non - conducting disc of radius `R`. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionProton , deuton and alpha particle of same kinetic energy are moving in circular trajectories in a constant magnetic field. The radii of proton , deuteron and alpha particle are respectively `r_(p), r_(d) and r_(alpha)`. Which one of the following relation is correct?
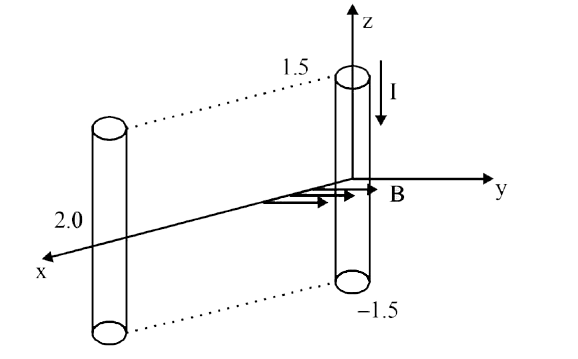
View SolutionA conductor lies along the ` z`-axis at ` -1.5 le z lt 1.5 m` and carries a fixed current of `10.0 A` in `- hat(a)_(z)` direction ( see figure). For a field `vec(B) = 3.0 xx 10^(-4) e^(-0.2x) hat(a)_(y) T`, find the power required to move the conductor at constant speed to `x = 2.0 m , y = 0 m ` in `5xx 10^(-3)s` . Assume parallel motion along the ` x-axis`.
View SolutionTwo coaxial solenoids of different radius carry current I in the same direction. `vec(F_1)` be the magnetic force on the inner solenoid due to the outer one and `vec(F_2)` be the magnetic force on the outer solenoid due to the inner one. Then
View SolutionA galvanometer of resistance `100Omega` has 50 divisions on its scale and has sensitivity of `20 mu`A/ division. It is to be converted to a voltmeter with three ranges, of `0-2V, 0-10V and 0-20V`. The appropriate circuit to do so is:
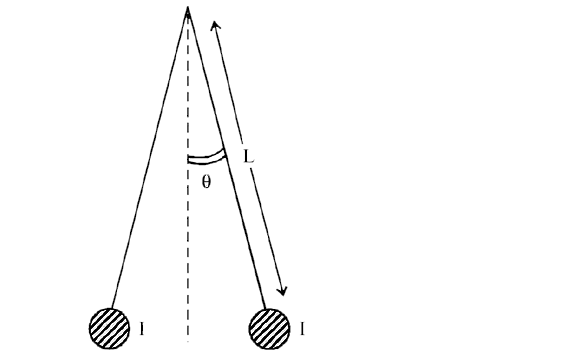
View SolutionTwo long current carrying thin wires , both with current `I`, are held by insulating threads of length `L` and are in equilibrium as shown in the gigure , With threads making an angle ` theta` with the vertical . If wires have mass ` lambda` per unit length then the value of `I` is :
View SolutionTwo identical wires `A and B` , each of length 'l', carry the same current `I`. Wire A is bent into a circle of radius `R and wire B` is bent to form a square of side 'a' . If ` B_(A) and B_(B)` are the values of magnetic field at the centres of the circle and square respectively , then the ratio `(B_(A))/(B_(B))` is :
View SolutionA galvanometer having a coil resistance of `100 omega` gives a full scale deflection , when a current of `1 mA` is passed through it. The value of the resistance, which can convert this galvanometer into ammeter giving a full scale deflection for a current of `10A` , is :
View SolutionA charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity `omega` with respect to normal axis then the magnetic moment of the loop is :
View SolutionThe sensitivity of a galvanometer is 60 division /A . When a shunt is used, its sensitivity becomes 10 division/A. If the galvanometer is of resistance `20 Omega `, the value of shunt used is
View SolutionIn a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 `kOmega` are used. The figure of merit of the galvanometer is 60 `muA//"division"`. In the absence of shunt resistance, the galvanometer produces a deflection of `theta =9` divisions when current flows in the circuit. The value of the shunt resistance that can cause the delflection of `theta//2`, is closet to :
View SolutionThe dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is `B_(1)` . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is ` B_(2)` . The ratio `(B_(1))/(B_(2))` is:
View SolutionA magnetic needle lying parallel to a magnetic field requires `W units` of work to turn it through `60^(@)`. The torque needed to maintain the needle in this position will be
View SolutionTwo identical magnetic dipoles of magnetic moments `2Am^2` are placed at a separation of `2m` with their axes perpendicular to each other in air. The resultant magnetic field at a mid point between the dipole is
View SolutionA Helmholtz coil has a pair of loops, each withN turns and radius R. They are placed coaxially at distance R and the same current I flows through the loops in the same direction. The magnitude of magnetic field at P, midway between the centres A and C, is given by [Refer to figure given below]:

View SolutionThe magnetic field at a point midway between two parallel long wires carrying currents in the same direction is `10 mu T`. If the direction of the smaller current among them is reversed, the field becomes `30 mu T` . The ratio of the larger to the smaller current in them is
View SolutionA thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of `40pi "rad s"^(-1)` about its axis, perpendicular to its plane. If the magnetic field at its centre is `3.8xx10^(-9)T`, then the charge carried by the ring is close to `(mu_(0)=4pi xx10^(-7)N//A^(2))`
View SolutionA galvanometer with its coil resistance `25 Omega` requires a current of 1 mA for its full deflection. In order to construct an ammeter to read up to a current of 2A, the approximate value of the shunt resistance should be :
View SolutionTwo long straight parallel wires, carrying (adjustable) currents `I_(1)` and `I_(2)` are kept at a distance d apart. If the force F between the two wires is taken as positive when the wire repel each other and negative when the wires attract each other, the graph showing the dependence of F, on the product `I_(1)I_(2)` would be:
View SolutionA wire carrying current I is tied between points P and Q and is in the shape of a circular arch of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by cross marked) in the vicinity of the wire. If the wire subtends and angle `2 theta_(0)` at the centre of the circle of which it forms an arch) then the tension in the wire is:
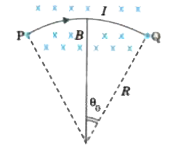
View SolutionA proton accelarted by a potential differnce `V = 500 kV` fieles through a unifrom transverse magnetic filed the induction `B = 0.54 T`. The field occupies a region of space `d = 10 cm` in thickness (Fig). Find the angle `alpha` through which the proton deviates from the initial direction of its motion.

View SolutionA `25cm` long solenoid has radius `2cm` and `500` total number of turns. It carries as current of `15A`.If it is equivalent to a magnet of the same size and magnetization `bar(M)` (magnetic moment//volume) then `|bar(M)|` is:
View SolutionConsider a thin metallic sheet perpendicular to the plane of the paper moving with speed `upsilon` in a uniform magnetic field B going into the plane of the paper (See figure.) If charge den- sities `sigma_1 and sigma_2` are induced on the left and right surfaces, respectively, of the sheet then (ignore fringe effects.)

View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as `B = B_0e^(-t//tau)`, where `B_0 and tau` are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time `(t to oo)` is :
View SolutionTo know the resistance of a galvanometer by half deflection method, a battery of emf V and resistance R is used to deflect the galvanometer by angle `theta` . If a shunt of resistance is needed to get half deflection then, G, R and S are related by the equation :
View SolutionA `50 Omega` resistance is connected to a battery of 5 V. A galvanometer of resistance `100 Omega` is to be used as an ammeter to measure current through the resistance, for this a resistancer `r_(s)` is connected to the galvanometer. Which of the following connections should be employed if the measured current is within 1% of the current without the ammeter in the circuit?
View SolutionIn a certain region static electric and magnetic fields exist. The magnetic field is given by `vec(B) = B_(0) (hat(i) + 2hat(j)-4hat(k))`. If a test charge moving with a velocity, `vec(upsilon) = upsilon_(0)(3hat(i)-hat(j) +2hat(k))` experience no force in that region, then the electric field in the region, in SI units, is-
View SolutionA magnetic dipole in a constant magnetic field has
View SolutionIn a coil of resistance `100 Omega` , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
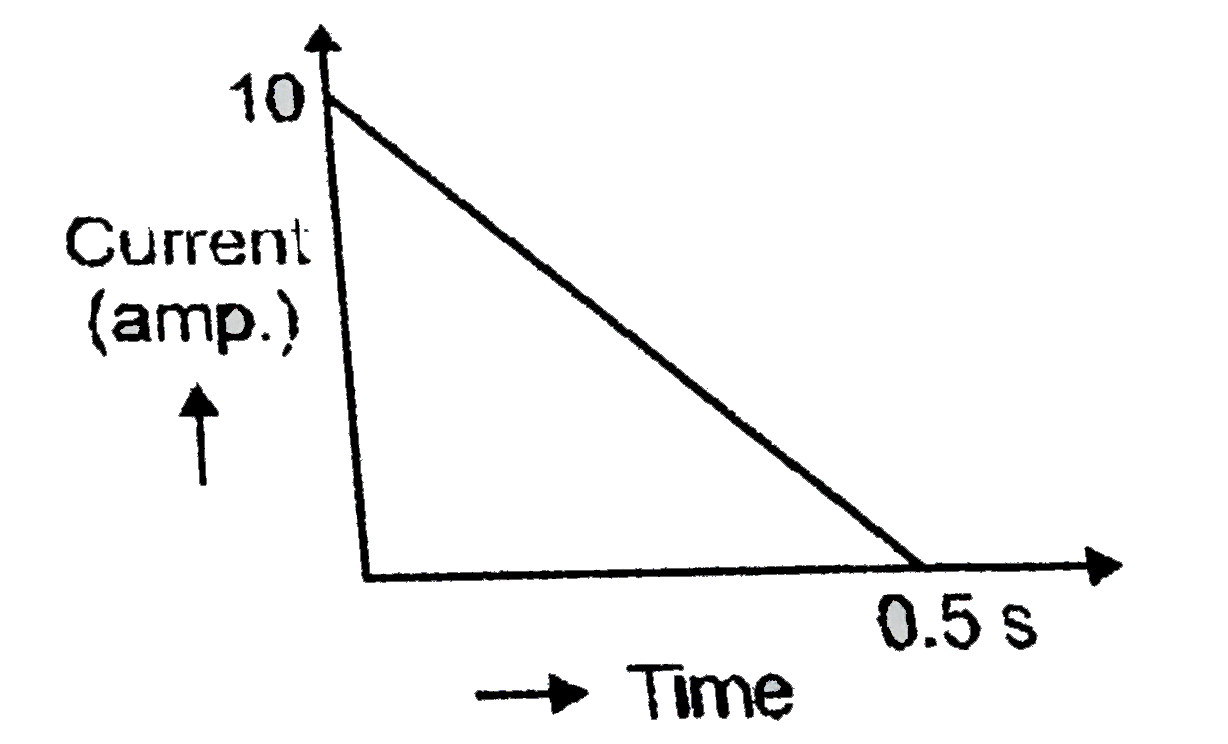
View SolutionWhen a current of 5mA is passed through a galvanometer having a coil of resistance `15Omega`, it shows full sacle deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range `0-10V` is:
View SolutionA negative test charge is moving mear a long straight wire carrying a current. The force acting on the test charge is parallel to the direction of the current. The motion of the charge is:
View SolutionA uniform magnetic field B of`0.3` T is along the positive Z-direction. A rectangular loop (abed) of sides `10 cm xx 5 cm` carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?
View SolutionA particle of the charged `q` and `mass m` moves in a circular orbit of radius `r ` with angular speed ` omega` . The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of mass `m` and charge `q` moves with a constant velocity `v` along the positive `x` direction. It enters a region containing a uniform magnetic field `B` directed along the negative `z` direction, extending from `x = a` to `x = b`. The minimum value of `v` required so that the particle can just enter the region `x gt b` is
View SolutionA conducting loop carrying a current `I` is placed in a uniform magnetic field pointing into the plane of the paper as shown. The loop will have a tendency to

View SolutionA loop carrying current `I` lies in the ` x-y ` plane as shown in the figure . The unit vector ` hat k` is coming out of the plane of the paper . The magnetic moment of the current loop is
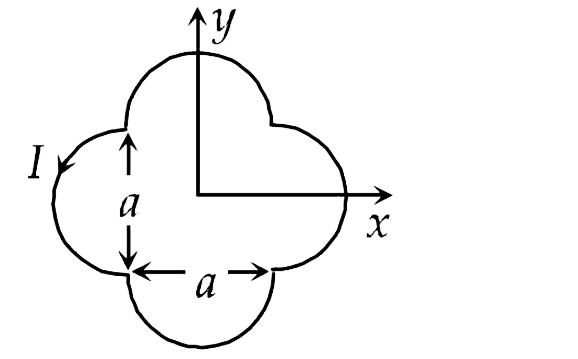
View SolutionAn electron moving with a speed u along the positive x-axis at `y=0` enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionA current carrying loop is placed in a uniform magnetic field in four different orientations , I,ii,iii & iv arrange them in the decreasing order of potential Energy`
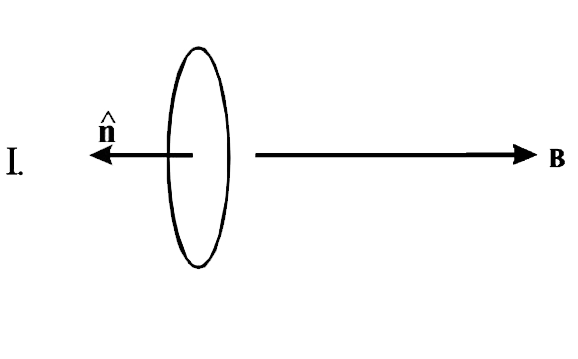
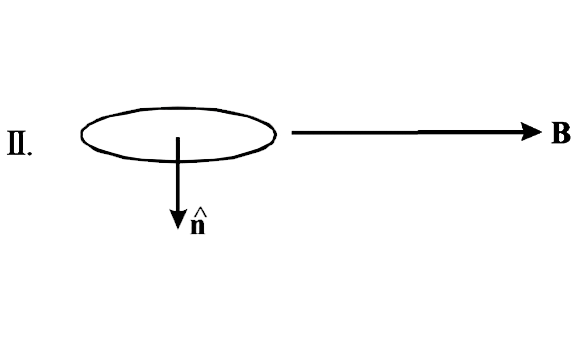


View SolutionAn ionized gas contains both positive and negative ions . If it is subjected simultaneously to an electric field along the ` +x` - direction and a magnetic field along the ` +y` - direction and the negative ions towardws `-y` - direction
View SolutionTwo long parallel wires are at a distance ` 2d` apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field `B` along the line `XX` is given by
View SolutionElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature `T_(C) (0)`. An interesting property of super conductors is that their critical temperature becomes smaller than `T_(C) (0)` if they are placed in a magnetic field, i.e., the critical temperature `T_(C) (B)` is a function of the magnetic field strength B. The dependence of `T_(C) (B)` on B is shown in the figure.
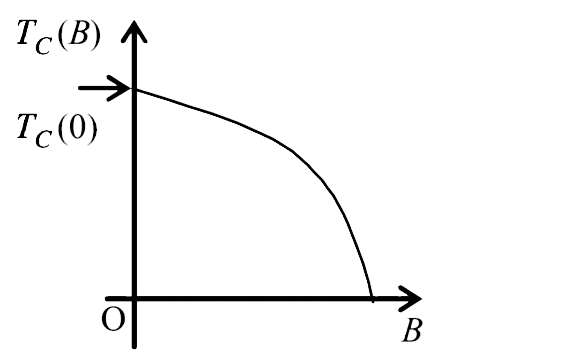 .
.
In the graphs below, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic fields `B_1`(solid line) and `B_2` (dashed line). If `B_2` is larget than `B_1` which of the following graphs shows the correct variation of R with T in these fields?
View SolutionA superconductor has `T_c(0)=100K`. When a magnetic field of `7*5tesla` is applied, its `T_c` decreases to `75K`. For this material, one can definitely say that when
View SolutionA magnetic field ` vec(B) = B_(0)hat(j)` , exists in the region `a ltxlt2a` , and `vec(B) = -B_(0) hat(j)` , in the region `2a lt xlt 3a`, where `B_(0)` is a positive constant . A positive point charge moving with a velocity `vec(v) = v_(0) hat (i)` , where `v_(0)` is a positive constant , enters the magnetic field at `x= a` . The trajectory of the charge in this region can be like

View SolutionA long insulated copper wire is closely wound as a spiral of `N` turns. The spiral has inner radius a and outer radius `b`. The spiral lies in the `xy`-plane and a steady current I flows through the wire. The`z`-component of the magetic field at the centre of the spiral is

View SolutionConsider the motion of a positive point charge in a region where area simultaneous uniform electric and magnetic fields ` vec(E) = E_(0) hat(j)` and ` vec(B) = B_(0) hat(j)`. At time ` t = 0` , this charge has velocity ` vec(v)` in the ` x-y `plane , making an angle ` theta` with the ` x-axis `. Which of the following option(s) is (are) correct for time ` t gt 0`?
View SolutionAn infinitely long hollow conducting cylinder with inner radius `(r )/(2)` and outer radius `R` carries a uniform current ra density along its length . The magnitude of the magnetic field , ` | vec(B)|` as a function of the radial distance `r` from the axis is best represented by
View SolutionA symmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is
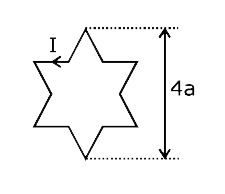
View SolutionA uniform magnetic field B exists in the region between x = 0 and `x = (3 R)/2` (region 2 in the figure) pointing normally into the plane of the paper. A particle with charge `+Q `and momentum p directed along X-axis enters region 2 from region 1 at point `P_(1) (y = - R)` . Which of the following option(s) is/are correct?

View Solution
COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS) questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- CHAPTER PRACTICE TEST
- COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (ASSERTION TYPE QUESTIONS)
- COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (INTEGER TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT (Exemplar Problems ) (Short Answer Type Questions )
- NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
- NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
- NCERT FILE (NCERT Additional Exercises)
- NCERT FILE (NCERT Textbook Exercises)
- PRACTICE PROBLEMS
- Revision Exercises (Additional Questions )
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer Questions )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer Questions )
- Revision Exercises (Very Short Answer Questions )
- SOLVED EXAMPLES
- Tough & Tricky (PROBLEMS )