Complete Solutions to Exercise of chapter CHEMICAL KINETIC & NUCLEAR CHEMISTRY of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETIC & NUCLEAR CHEMISTRY |
| NARENDRA AWASTHI | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The differential rate law equation for the elementary reaction `A+2Boverset(k)to3C`, is
View SolutionThe rate of a reaction is expressed in different ways as follows:
`+(1)/(2)(d[C])/(dt)=-(1)/(3)(d[D])/(dt)=+(1)/(4)(d[A])/(dt)=-(d[B])/(dt)`
the reaction is
View SolutionIn the reaction , `A+2Bto6C+2D`, if the initial rate `-(d[A])/(dt)` at t= 0 is `2.6xx10^(-2)Msec^(-1)`, what will be the value of `-(d[B])/(dt)` at t=0?
View SolutionFor the reaction `2AtoB+3C`, if `-(d[A])/(dt)=k_(1)[A]^(2),-(d[B])/(dt)=k_(2)[A]^(2),-(d[C])/(dt)=k_(3)[A]^(2)` the correct reaction between `k_(1),k_(2)` and `k_(3)` is :
View SolutionThe rate constant of `n^(th)` order has units :
View SolutionWhich of the following statement is incorrect?
View SolutionWhich of the following relation is correct for `k_(f)` and `k_(b)` in an equibilirium process that contains equal moles of rectants and products.
View SolutionListed in the table are forward and reverse rate constants for the reaction
`2NO(g)hArrN_(2)(g)+O_(2)(g)`
`{:(,Temperature(K),k_(f)(M^(-1)s^(-1)),k_(b)(M^(-1)s^(-1))),(,1400,0.29,1.1xx10^(-6)),(,1500,1.3,1.4xx10^(-5)):}`
Select the correct statement
View SolutionThe rate of constatnt depends on
View SolutionIn the following reaction, how is the rate of appearance of the underline product related to the rate of disappearance of the underlined reactant?
`BrO_(3)^(-)(aq)+ul(5Br^(-))(aq)+6H^(+)(aq)toul(3Br_(2))_((1))+3H_(2)O_((1))`
View SolutionConsider a reaction `A(g)overset(k=0.1 M min^(-1))to2B(g)`. If initial concentration of A is 0.5 M then select correct graph.
View SolutionWhich of the following statement is incorrect?
View SolutionThe molecularity of a complex reaction given below is :
`2N_(2)O_(5)(g)to4NO_(2)(g)+O_(2)(g)`
View SolutionDecomposition of `NH_(4)NO_(2)(aq` into `N_(2)(g)` and `2H_(2)O(l)` is first order reaction.
View SolutionDecomposition of `Hl (g)` on Gold surface is zero order reaction. Initially, few moles of `H_(2)` are present in container then which of the following graph is correct ?
View SolutionConsider the plots for the types of reaction
`nAtoB+C`

These plots respectively correspond to the reaction orders :
View SolutionIf decompositon reaction `A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be :
View SolutionConsider the plots for the types of reaction
`nAtoB+C`

These plots respectively correspond to the reaction orders :
View SolutionFor a zero order reaction, the plot of concentration, vs time is linear with
View SolutionWhat will be the order of reaction for a chemical change having `log t_((1)/(2))` vs log a? ( where a = initial concentration of rectant, `t_((1)/(2))` =half life)
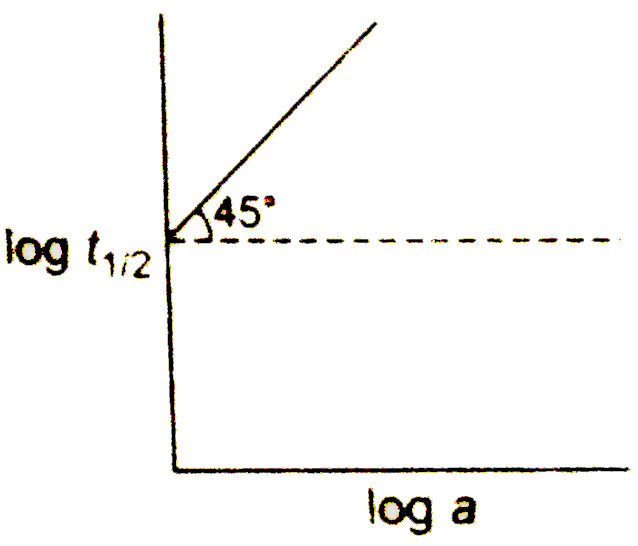
View SolutionA graph between `log t_((1)/(2))` and log a (abscissa), a being the initial concentration of A in the reaction For reaction `Ato`Product, the rate law is :
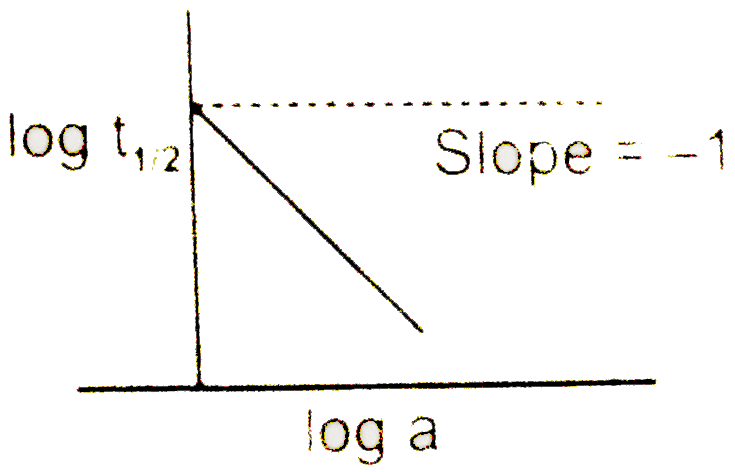
View SolutionFor the reaction`AtoB`, for which graph between half life `(t_(1//2)) and initial concentration (a) of the rectant is given below

Hence graph between `-(d[A])/(dt)` and time will be:
View SolutionFor the ideal gaseous reaction, the rate is generally expressed in terms of `(dP)/(dt)` instead of `(dC)/(dt)` or `(dn)/(dt)` (where C=`(n)/(V)` is concentration and n the no. of moles). What is the relation among these three expressions if T and V are constant?
View Solution`A_(2)+B_(2)to2AB`, R.O.R.=`k[A_(2)]^(a)[B_(2)]^(b)`
`{:(,"Initial"[A_(2)],"Initial"[B_(2)],R.O.R.(r) Ms^(-1)),(,0.2,0.2,0.04),(,0.1,0.4,0.04),(,0.2,0.4,0.08):}`
Order of reaction with respect to `A_( 2)` and `B_(2)` are respectively :
View SolutionFor a reaction initial rate is given as : `R_(0)=k[A_(0)]^(2)[B_(0)]`. By what factor, the initial rate of reaction will increase if initial concentration is taken 1.5 times and B is tripled?
View SolutionFor `A_((s))+B_((s))toC_((s))`,rate=`k[A]^(1//2)[B]^(2)`, if initial concentration of A and B are increased by factors 4 and 2 respectively, then the initial rate is changed by the factor:
View SolutionReaction `AtoB` follows second order kinetics. Doubling the concentration of A wil increase the rate of formation of B by a factor of :
View SolutionThe reaction of `A_(2)` and `B_(2)` follows the equation
`A_(2)(g)+B_(2)(g)to2AB(g)`
The following data were observed
`{:(,[A_(2)]_(0),[B_(2)]_(0),"Initial rate of appearance of AB(g)(in" Ms^(-1)),(,0.10,0.10,2.5xx10^(-4)),(,0.20,0.10,5xx10^(-4)),(,0.20,0.20,10xx10^(-4)):}`
The value of rate constatnt for the above reaction is :
View SolutionThe unit of rate constant of elementary reaction depends upon the
View SolutionSelect the rate law that corresponds to the datashown for the reaction `A+BtoC`
`{:(,Exp.,[A],[B],Rate),(,1,0.012,0.035,0.10),(,2,0.024,0.070,0.80),(,3,0.024,0.035,0.10),(,4,0.012,0.070,0.80):}`
View SolutionAn elementary reaction A and B is second order reaction. Which of the following rate equation must be correct?
View SolutionIf `a` is the initial concentration of the rectant, the half life period of the reaction of `n^(th)` order is inversely proportional to :
View SolutionWhich of the following expressions is correct for zero and first order respectively [Where a is initial concentration]?
View SolutionThe unit of rate constant of zero order and first order chemical reactions are respectively :
View SolutionThe unit of rate of reaction and rate of rate constant are same for a :
View Solution`CH_(3)COOC_(2)H_(5)(aq)+H_(2)O(l)overset(H^(+)(aq))toCH_(3)COOH(aq)+C_(2)H_(5)OH(aq)`. What type of reaction is this?
View SolutionWhen ethyl acetate was was hydrolysedin presemce of 0.1 M HCl, the rate constant was found to be `5.4xx10^(-5)s^(-1)`. But in presence of 0.1 M `H_(2)SO_(4)` the rate constant was found to be `6.25xx10^(-5)s^(-1)`. Thus it may be concluded that:
View SolutionFor an elementary reaction `2A+B rarr A_(2)B` if the volume of vessel is quickly reduced to half of it's original volume then rate of reaction will `:`
View SolutionIn the reaction `AtoB+C`, rate constant is `0.001Ms^(-1)`. If we start with 1 M of A then conc. Of A and B after 10 minutes are respectively :
View SolutionFor a reaction `Aoverset(k_(r)=0.6M min^(-1))to2B`
starting with 1 M of 'A' only, concentration of B (in M) after 100 sec. and 200 sec. is respectively?
View SolutionFor the zero order reaction `AtoB+C`, initial concentration of A is 0.1 M. If [A]=0.08 M after 10 minutes,then its half-life and completion time are respectively :
View SolutionFor an elementary reaction , `X(g)toY(g)+Z(g)`
the half life period is 10 min. In what period of time would the concentration of X be reduced to 10% of original concentration?
View SolutionIn the presence of acid, the initial concentration, of cane sugar was reduced form `0.2 M` to `0.1` in `5 hr` and to `0.05 M` in `10 hr`. The reaction must be of
View SolutionA first order reaction is 75% completed in 100 minutes. How long time will it take for its 87.5% completion?
View SolutionThe rate constant for a first order reaction whose half life is 480 sec, is :
View SolutionRate constant k=2.303 `min^(-1)` for a particular reaction. The initial concentration of the reactant is 1 mol`//`litre then rate of reaction after 1 minute is:
View SolutionFor the reaction `3A(g)overset(k)toB(g)+C(g)` k is `10^(-4)L//mol.min`.
If [A] = 0.5M then the value of `-(d[A])/(dt)`(in `ms^(-1)` is:
View Solution99% of a first order reaction was completed in 32 in. When wil 99.9% of the reaction complete?
View SolutionWhich of the following represents the expression for 3/4 th life of 1st order reaction
View SolutionConsider following two competing first ordr reactions,
`Poverset(k_(1))rarrA+B,Qoverset(k_(2))rarrC+D`
if `50%` of the reaction oof P wascompleted when `96%` of Q was complete ,then the ratio `(k_(2)//k_(1))` will be :
View SolutionFor the reaction
(i) `Aoverset(k_(I))toP`
(ii) `Boverset(K_(II))toQ`, following observation is made.
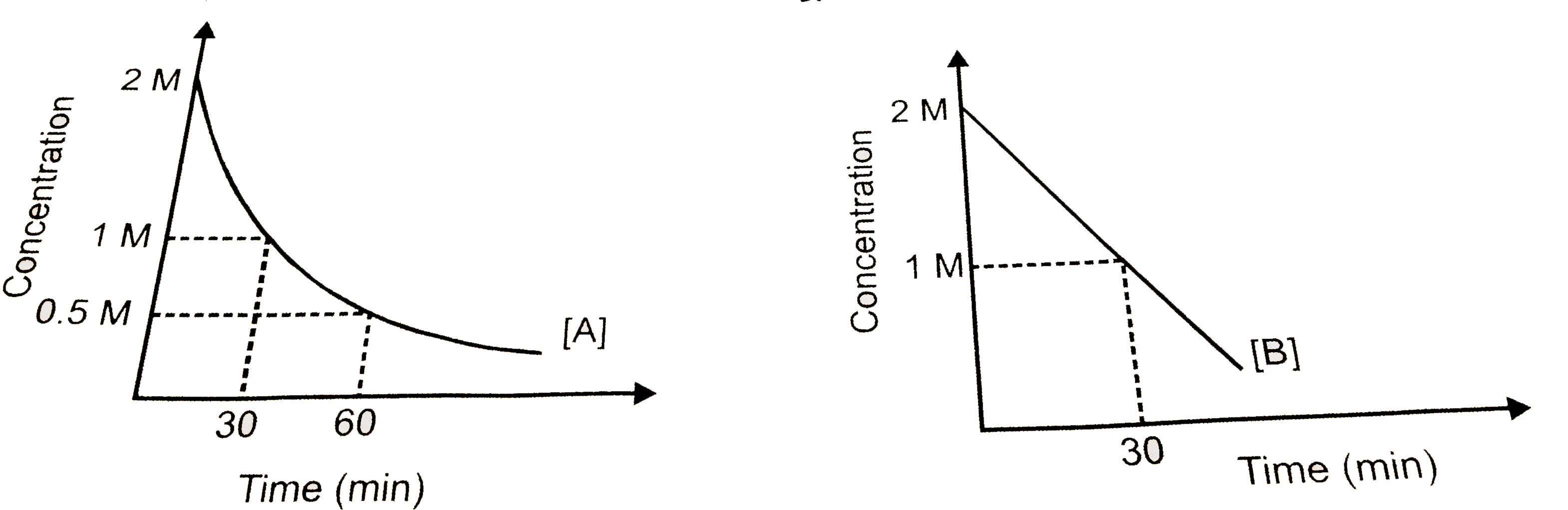
Calculate `(k_(1))/(k_(II))`, where `k_(I)` and `k_(II)` and rate constant for the respective reaction.
View SolutionFor the homogenous gaseous reaction `Ato3B`, if pressure after time t was `P_(t)` and after completion of reaction, pressure was `P_(oo)` then select correct relation
View SolutionThe half-life of first order decomposition of `NH_(4)NO_(3)` is 2.10 hr at 288 K temperature
`NH_(4)NO_(3)(aq)toN_(2)O(g)+2H_(2)O(l)`. If 6.2 of `NH_(4)NO_(3)` is allowed to decompose, the required for `NH_(4)NO_(3)` to decompose 90 % is :
View SolutionFor a first order homogeneous gaseous reaction `Ato2B+C`, if the total pressure after time t was `P_(t)` and after a long time `(to to oo)` was `P_(oo)` then k in terms of `P_(t),P_(oo)` and t is
View SolutionThe decomposition of azo methane, at certain temperature acccording to the equation `(CH_(3))_(2)N_(2)toC_(2)H_(6)+N_(2)` is a first order reaction.
After 40 minutes from the start, the total pressure developed is found to be 350 mm Hg in place of initial pressure 200 mm Hg of azo methane. The value of rate constant k is :
View SolutionThe hydrolysis of sucrose was studied with the help of calorimeter and following data were
`{:(,"Collected time (min.)",:0,70,oo),(,"observed rotation (degrees)",:44,16.5,-11):}`
the time taken when reaction mixture wil be optically inactive ? (Given : In 2=0.7,in 3=1.1, in 5=1.6)
View SolutionFor a partiocular reaction with initial conc. Of the rectents as `a_(1)` and `a_(2)`, the half-life period are `t_(1)` and `t_(2)` respectively. The order of the reaction (n) is given by :
View SolutionThe value of `t_(0.875)/(t_(0.50)` for `n^(th)` order reaction is
View Solution`AtoB` first order reaction A is ooptical active and B is optically inactive. A series of experiment were conducted on a solution of A
`{:(,"Time",0,60 min,oo),(,"optical rotation",82^(@),77^(@),2^(@)):}`
assume some imurity is present calculate the otical rotation for 5 hours.)
(Given in 1.066=0.064, `e^(0.16)`=1.17)
View SolutionAt 300 K the half-life of a sample of a gaseous compound initially at 1 atm is 100 sec. When the pressure is 0.5 atm the half-life is 50 sec. The order of reaction is :
View SolutionA decomposes as
 . The rate of appearance of B, taking 2 M concentration of A, is equal to :
. The rate of appearance of B, taking 2 M concentration of A, is equal to :
View SolutionFor an endothermic reaction energy of activation is `E_(a)` and enthalpy of reaction is `DeltaH` (both in kJ `"mol"^(-1)` ) Minimum value of `E_(a)` will be
View SolutionThe activation energy of the reaction, `A+BtoC+D+38` kcal is 20 kcal. What would be the activation energy pof the following reaction.
`C+DtoA+B`
View SolutionWhen the activation energies of the forward and backward reactions are equal, then :
View SolutionFor an exothermic chemical process ocuuring in two process occuring in two steps as follows
`(i)A+BtoX("slow")" "(ii)XtoAB("fast")`
The progress of reaction can be best described by :
View SolutionSelect the correct diagram for an endothermic reaction that proceeds through two steps with the second steps is rate determining :
View Solution`k_(34^(@))/k_(35^(@)) lt 1`, then
View SolutionThe plot of In 1/T is linear with slope of :
View SolutionRate constant for a chemical reaction taking place at 500K is expressed as `K=A. e^(-1000)` The activation energy of the reaction is :
View SolutionFor a complex reaction `A overset(k) rarr `products
`E_(a1)=180kJ //mol e,E_(a2)=80kJ//mol ,E_(a3)=50kJ//mol`
Overall rate constant `k` is related to individual rate constant by the equation `k=((k_(1)k_(2))/(k_(3)))^(2//3)`. Activation energy `( kJ//mol )` for the overall reaction is `:`
View SolutionFor reaction A `rarr` B , the rate constant `K_(1)=A_(1)(e^(-E_(a_(1))//RT))` and the reaction `X rarr Y` , the rate constant `K_(2)=A_(2)(e^(-E_(a_(2))//RT))` . If `A_(1)=10^(9)`, `A_(2)=10^(10)` and `E_(a_(1))`=1200 cal/mol and `E_(a_(2))` =1800 cal/mol , then the temperature at which `K_(1)=K_(2)` is : (Given , R=2 cal/K-mol)
View SolutionThe activation energies of the forward and backward reactions in the case of a chemical reaction are 30.5 and 45.5 KJ/mol , respectively . The reaction is:
View SolutionA reaction rate constant is given by : `K= 1.2 xx10^(14)e^((-25000)/(RT)) sec^(-1)`. It means :
View SolutionThe temperature coefficient of a reaction is
View SolutionWhich graph shows zero activation energy ?
View SolutionA homogenous catalytic reaction takes place through the three alternative plots A, B, and C shown in the given figure. Which one of the following indicates the relative ease with which the reaction can take place?

View SolutionThe rate of a reaction gets doubled when temperature increase by `27^(@) C "to" 37^(@)` . By what factor will it change for the temperature range `17^(@)` C to `27^(@)` C
View SolutionWhich of the following expkains the increase of reaction rate by a catalyst?
View SolutionCollision theory satisfactorily explains
View SolutionFor the first order reaction `A rarr B +C` , carried out at `27^(@)` C . If `3.8 xx 10^(-16)%` of the reactant molecules exists in the activated state , the `E_(a)` (activation energy) of the reaction is:
View SolutionFor a reaction the following mechanism has been proposed , `2A+BtoD+E`
`A+BtoC+D` (slow), `A+CtoE`(fast)
The rate law a expression for the reaction is
View SolutionA reaction `A_(2)+B_(2)to2AB` occurs by the following mechanism:
`A_(2)hArr A+A`…………(fast)
`A+B_(2)toAB+B`……….(slow)
`A+BtoAB`…………..(fast) Its order would be:
View SolutionChemical reaction occurs as a result of collisions between reacting molecules. Therefore, the reaction rate is given by
View SolutionRadioactivity is affected by:
View SolutionThe radiation from naturally occuring radioactive substance as seen after deflection by a magnetic field in one direction are :
View SolutionDuring `alpha`-decay:
View SolutionAtoms `._(7)X^(A),._(8)Y^(B)` and `._(9)Z^(17)` are such that `._(8)Y` is an isobar of `._(7)X` and atom `._(9)Z^(17)` is isotone of `._(8)Y`. Mass no. of `X` and no of neutrons in `Y` are respectively `:`
View Solution`._(90)Th^(234)` disintegrates to give `._(82)Pb^(206)Pb` as the final product. How many alpha and beta particles are emitted during this process ?
View SolutionAn isotone of `._(32)^(76)Ge` is-
(a) `._(32)^(77)Ge`
(b)`._(33)^(77)As`
(c)`._(34)^(77)Se`
(d)`._(34)^(78)Se`
View SolutionIsodiaphers are atoms having:
View SolutionThe number of neutrons accompanying the formation of `._(54)Xe^(139)` and `._(38)Sr^(94)` from the absorption of a slow neutron by `._(92)U^(235)`, followed by nuclear fission is
View SolutionComplete the following nuclear equation by suppling the symbol for the other product of the fission :
`._(92)^(235)U+_(0)^(1)n rarr _(38)^(94)Sr +………+2_(0)^(1)n`
View Solution`X rarr _(82)^(206)Pb+_(2)^(4)He` .In this reaction predict the position of group of X:
View Solution`._(90)Th` is a member of III group . After losing `alpha`-particle it forms a new element belonging to :
View SolutionAlpha decay of `._(92)^(238)U` forms `._(90)^(234)Th`. What kind of decay from `._(90)^(234)Th` produces `._(84)^(234)Ac` ?
View SolutionA radioactive sample had an initial activity of 56 dpm . After 69.3 minutes , it was found to have an activity of 28 dpm , the number of atoms in a sample having an activity of 100 dpm is `10^(x)` . The value of x is …….
View SolutionA radioactive sample has initial activity of 28 dpm 30 minutes later its activity 14 dpm . How many atoms of nuclide were present initially?
View SolutionThe value of decay constant of `Co^(60)` is `2.5xx 10^(-7)"min"^(-1)` . The activity of 2.0 g of the sample is nearly :
View SolutionHalf-life `(t_(1//2))` for a radioactive decay is 6930 sec. The time required to fall the rate of decay to `((1)/(100))^(th)` of its initial value is:
View SolutionA sample of radioactive substance is found 90% of its initial amount after one day . What % of the original sample can be found after 3 days?
View Solution
Exercise questions and complete solutions for chapter CHEMICAL KINETIC & NUCLEAR CHEMISTRY of NARENDRA AWASTHI of Class 12
All Exercises from NARENDRA AWASTHI Class 12 CHEMISTRY CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- Exercise
- Level 1 (Q.123 To Q.150)
- Level 1 (Q.3 To Q.32)
- Level 1 (Q.33 To Q.62)
- Level 1 (Q.63 To Q.92)
- Level 1 (Q.93 To Q.122)
- Level 2
- Level 2 (Q.3 To Q.32)
- Level 2 (Q.33 To Q.35)
- Level 3 - Assertion - Reason Type Questions
- Level 3 - One Or More Answers Are Correct
- Level 3 - Passage
- Level 3 - Subjective Problems