Complete Solutions to Short Answer Type Questions of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| NCERT EXEMPLAR | Short Answer Type Questions |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
For a loaded die, the probabilities of outcomes are given as under: `P(1)=P(2)=2/(10),P(3)=P(5)=P(6)=1/(10)a n dP(4)=3/(10)` The die is thrown two times. Let A and B be the events as defined below A=Getting same number each time, B=Getting a total score of 10 or more. Determine whether or not A and B are independent events.
View SolutionRefer to question 1 above. If the die were fair, determine whether or not the events A and B are independent.
View SolutionThe probability that atleast one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate `P(barA)+P(barB)`.
View SolutionA bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that atleast one of the three marbles drawn be black, if the first marble is red?
View SolutionTwo dice are thrown together and the total score is noted. The event E, F and G are a total 4, a total of 9 or more, and a total divisible by 5, respectively. Calculate `P(E),P(F)a n dP(G)` and decide which pairs of events, if any, are independent.
View SolutionExplain why the experiment of tossing a coin three times is said to have Binomial distribution.
View SolutionIf A and B are two events such
`P(A)=1/2,P(B)=1/3and P(AcapB)=1/4`,then find
(i) P(A/B). (ii) P(B/A).
(iii) P(A'/B). (iv) P(A'/B').
View SolutionThree events A, B and C have probalities `2/5,1/3 and 1/2`, respectively. If, `P(AcapC)=1/5and P(BcapC)=1/4`, then find the values of P(C/B) and `P(A'capC')`
View SolutionLet `E_(1) and E_(2)` be two independent events such that `P(E_(1))=P_(1)` and `P(E_(2))=P_(2)`, describe in words of the events whose probabilities are
(i) `P_(1)P_(2)` (ii) `(1-P_(1))P_(2)`
(iii) `1-(1-P_(1))(1-P_(2))` (iv) `P_(1)+P_(2)-2P_(1)P_(2)`
View SolutionA discrete random variable X has the probability distribution as given below
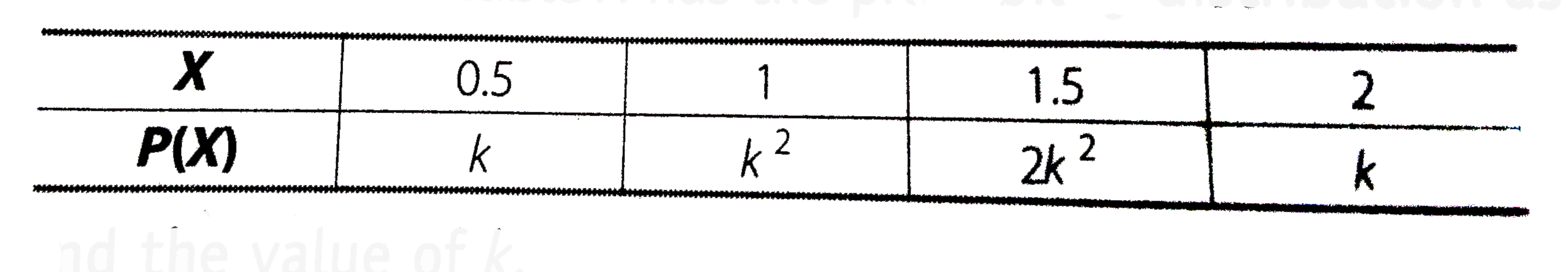
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionProve that
(i) `P(A)=P(AcapB)+P(AcapbarB)`
(ii) `P(AcupB)=P(AcapB)+P(AcapbarB)+P(barAcapB)`
View SolutionIf x is the number of tails in three tosses of a coin, then determine the standard deviation of X.
View SolutionIn a dice game , a player pays a stake of ₹1 for each throw of a die. She receives ₹5, if the die shows a 3, ₹ 2, if the die shows a 1 or 6 and nothing otherwise, then what is the player's expected profit per throw over a long series of throws?
View SolutionThree dice are thrown at the same time. Find the probability of getting three two's, if it is known that the sum of the numbers on the dice was 6
View SolutionSuppose 10000 tickets are sold in a lottery each for ₹ 1. First prize is of ₹ 3000 and the second prize is of ₹ 2000. There are three third prizes of ₹ 500 each. If you buy one ticket, then what is your expectation?
View SolutionA bag contrains 4 white and 5 black blls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.
View SolutionA bag contains 3 white and 2 black balls and another bag contains 2 white and 4 black balls. One bag is chosen at random. From the selected bag, one ball is drawn. find the probability that the ball drawn is white.
View SolutionA box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then, another ball is drawn at random. What is the probability of second ball being blue?
View SolutionFour cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are king?
View SolutionIf a die is thrown 5 times, then find the probability that an odd number will come up exactly three times.
View SolutionIf ten coins are tossed, then what is the probability of getting atleast 8 heads?
View SolutionThe probability of a man hitting man hitting target is 0.25. If he shoots 7 times, then what is the probability of his hittiing atleast twice ?
View SolutionA lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then what is the probability that there will be atleast one defective watch ?
View SolutionConsider the probability distribution of a random variable X

Calculate
(i) `V( X/2)` (ii) Variance of X.
View SolutionThe probability distribution of a random variable X is given below
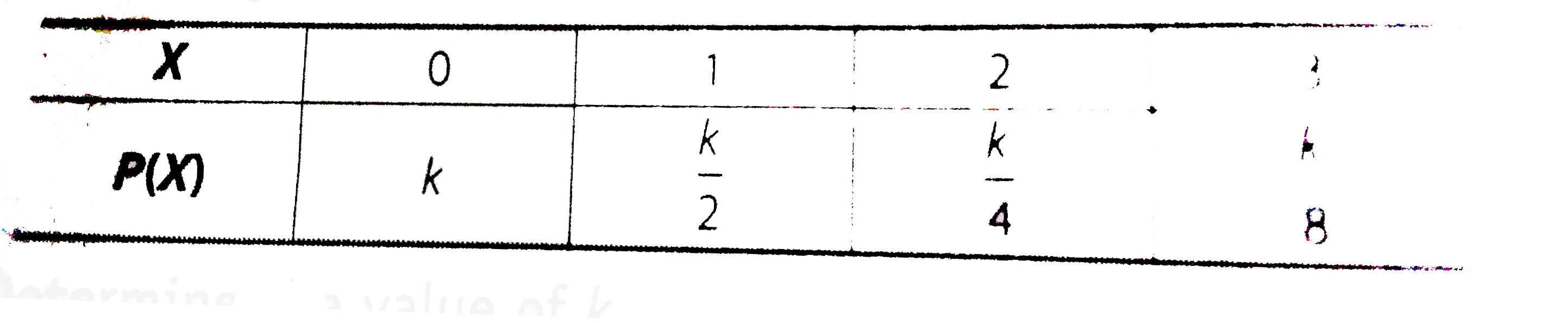
(i) Determine the value of K .
(ii) Determine `P(Xle2)andP(Xgt2)`.
(iii) Find P`(Xle2)+P(Xgt2)`.
View SolutionFor the following probability distribution determine standard deviation of the random variable X.

View SolutionA biased die is such that P(4)`=1/10` and other scores being equally likely. The die tossed twice. If X is the number of four seen, then find the variance of the random variable X.
View SolutionA die is thrown three times. Let `X` be the number of twos seen. Find the expectation of `X` .
View SolutionTwo baised dice are thrown together. For the first die `P(6)=1/2` , other scores being equally likely while for the second die, `P(1)=2/5` and other scores are equally likely. Find the probability distribution of the number of ones seen.
View SolutionTwo probability distributionof the discrete random variable X and Y are given below.

Prove that `E(Y^(2))=2E(X)`.
View SolutionA factory produces bulbs. The probability that any one bulb is defective is `1/50` and they are packed in 10 boxes. From a single box, find the probability that
(i) none of the bulbs is defective.
(ii) exactly two bulbs are defective.
(iii) more than 8 bulbs work properly.
View SolutionSuppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was fair coin?
View SolutionSuppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed, 30 % of the people have blood groups O. If a left handed person os selected at random, what is the probability that he/she will have blood group O?
View SolutionIf two natural numbers r and s are drawn one at a time, without replacement from the set S={1,2,3,….n}, then find P`(rlep//slep)` where p`in`S.
View SolutionFind the probability distribution of the maximum of two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
View SolutionThe random variable X can take only the values 0,1,2. If
`P(X=0)=P(X=1)=p and E(X^(2))=E[X]`,
then find valu of p.
View SolutionFind the varience of the following distribution.
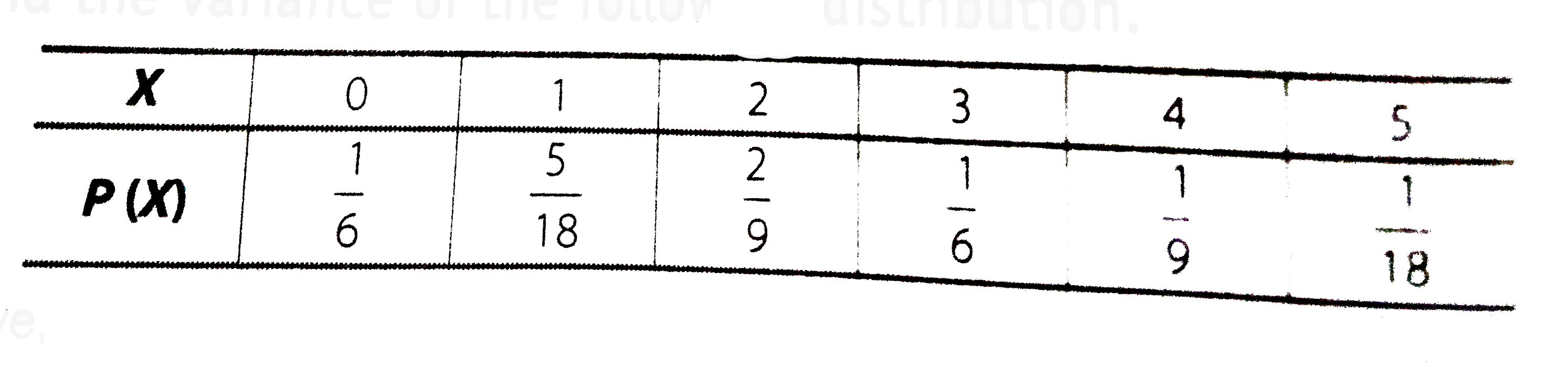
View SolutionA and B throw a pair of dice alternately. A wins the game, if he gets a total of 6 anfd B wins, if she gets a total of 7. If a starts the game, then find the probabbility of winning the game by A in third throw of the pair of dice.
View SolutionTwo dice are tossed. Find whether the following two events A and B are independent A={(x,y):x+y=11} and B={(x,y):`xne5`}, where (x,y) denotes a typical sample point.
View SolutionAn urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k balls of the same colour as that of the ball drawn. a ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.
View Solution
Short Answer Type Questions questions and complete solutions for chapter PROBABILITY of NCERT MATHS (ENGLISH) of Class 12