Complete Solutions to Illustration of chapter THREE DIMENSIONAL COORDINATE SYSTEM of Class 12 book with complete answers and questions

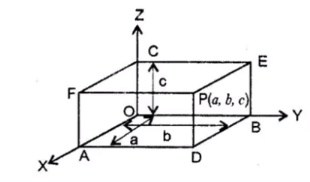
In the following figure, if the coordinates of `P` are `(a,b,c)` then the coordinates of `A,B` and `C` are respectively

In Fig 4 the coordinates of point D are

In fig. 28.7 if the coordinates of point `P\ a r e\ (a , b , c)` then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point `P` on the coordinate planes `X Y ,\ Y Z\ a n d\ Z Xdot` Find the perpendicular distances of point `P` from `X Y , Y Z\ a n d\ Z X-` planes. Find the perpendicular distances of the point `P` fro the coordinate axes. Find the coordinates of the reflection of `P` are `(a , b , c)` . Therefore `O A=a ,\ O B=b\ n d\ O C=cdot`

In fig. 28.7 if the coordinates of point `P\ a r e\ (a , b , c)` then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point `P` on the coordinate planes `X Y ,\ Y Z\ a n d\ Z Xdot` Find the perpendicular distances of point `P` from `X Y , Y Z\ a n d\ Z X-` planes. Find the perpendicular distances of the point `P` fro the coordinate axes. Find the coordinates of the reflection of `P` are `(a , b , c)` . Therefore `O A=a ,\ O B=b\ n d\ O C=cdot`

In fig. 28.7 if the coordinates of point `P\ a r e\ (a , b , c)` then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point `P` on the coordinate planes `X Y ,\ Y Z\ a n d\ Z Xdot` Find the perpendicular distances of point `P` from `X Y , Y Z\ a n d\ Z X-` planes. Find the perpendicular distances of the point `P` fro the coordinate axes. Find the coordinates of the reflection of `P` are `(a , b , c)` . Therefore `O A=a ,\ O B=b\ n d\ O C=cdot`

In the adoining figure if the coordinates of point P are `(a,b,c)` write the coordinates of A,B,C,D,E and F.

Planes are drawn parallel to the coordinate planes through the point `P(x_1, y_1,\ z_1)` and `Q(x_2, y_2, z_2)` . Find the length of the edges of the parallelopiped so formed.

The perpendicular distance of the point `(6,5,8)` from y-axis is

If the extremities of the diagonal fo a square are (1,-2,3) and (2,-3,5), then the length of the side is `sqrt(6)` b. `sqrt(3)` c. `sqrt(5)` d. `sqrt(7)`

Find the coordinates of a point equidistant from th four points `O(0,0,0),A(a ,0,0),B(0,b ,0)a n dC(0,0,c)dot`

Determine the point in `X Y-p l a n e` whcih is equidistant from three points `A(2,0,3),B(0,3,2)a n dC(0,0,1)dot`

The cosine of the angle of the triangle with vertices `A(1,-1,2),B(6,11,2)` and `C(1,2,6)` is

Let `P(2,-1,4)` and `Q(4,3,2)` are two points and as point `R` on `PQ` is such that `3PQ=5QR`, then the coordinates of `R` are

Let `A(2,-1,4)` and `B(0,2,-3)` be the points and C be a point on AB produced such that `2AC=3AB`, then the coordinates of C are

Find the ratio in which the line joining the points `(1,2,3)a n d(-3,4,-5)` is divided by the `x y-p l a n e` . Also, find the coordinates of the point of division.

In triangle ABC the mid point of the sides AB, BC and AC respectively (l, 0, 0), (0, m, 0) and (0, 0, n). Then, `(AB^2+BC^2+CA^2)/(l^2+m^+n^2)` is equal to

Find the coordinate of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the i. yz-plane ii. zx-plane.

Find the ratio in which the join the `A(2,1,5)a n dB(3,4,3)` is divided by the plane `2x+2y-2z=1.` Also, find the coordinates of the point of division.

If a vector `vecA` makes an angles `alpha, beta and gamma` respectively with the x, y and z axes respectively. Then `sin^(2)alpha + sin^(2)beta + sin^(2)gamma` is equal to

If a line makes angles `alpha,beta,gamma` with the axes respectively tehn `cos2alpha+cos2beta+cos2gamma=` `-2` b. `-1` c. `1` d. 2

If a line makes angle `pi/3\ a n d\ pi/4` with x-axis and y-axis respectively, then the angle made by the line with z-axis is `pi//2` b. `pi//3` c. `pi//4` d. `5pi//12`

The direction cosines of a vector `vecr` which is equally inclined with OX,OY and OZ are

A vector ` vec r` is inclined at equal to `O X ,O Ya n dO Zdot` If the magnitude of ` vec r` is 6 units, find ` vec rdot`

If OA is equally inclined to OX,OY ,OZ and if A is `sqrt(3)` units from the origin then the cordinates of A are

If `1/2,1/3,n` are direction cosines of a line, then the value of `n` is

If the direction ratios of a line are proportional to ( 1, -3, 2 ) then its direction cosines are `1/(sqrt(14)),-3/(sqrt(14)),2/(sqrt(14))` b. `1/(sqrt(14)),2/(sqrt(14)),3/(sqrt(14))` c. `-1/(sqrt(14)),3/(sqrt(14)),2/(sqrt(14))` d. `-1/(sqrt(14)),-2/(sqrt(14)),-3/(sqrt(14))`

The projections of a line segment on the coordinate axes are 12,4,3 respectively. The length and direction cosines of the line segment are

If `vecr` is a vector of magnitude 21 and has direction ratios 2, -3 and 6, then find `vecr`.

If `P(x,y,z)` is a point on the line segment joining Q(2,2,4) and R(3,5,6) such that the projection of `vec(OP)` on the axes are `13/9, 19/5, 26/5` respectively, then P divides QR in the ratio:

The direction cosines of the line passing through `P(2,3,-1)` and the origin are

The projection of the line segment joining the points `A(-1,0,3)` and `B(2,5,1)` on the line whose direction ratios are proportional to 6,2,3 is

The direction cosines of a vector `vecr` which is equally inclined with OX,OY and OZ are

A vector ` vec r` is inclined at equal to `O X ,O Ya n dO Zdot` If the magnitude of ` vec r` is 6 units, find ` vec rdot`

Find the angle between two lines whose direction ratios are proportional to `1,1,2a n d(sqrt(3)-1),(-sqrt(3)-1),4` .

If `P(0,1,2),\ Q(4,-2,1)a n d\ O(0,0,0)` are three points then ` P O Q=` `pi/6` b. `pi/4` c. `pi/3` d. `pi/2`

If A,B,C,D are (2,3,-1),(3,5,-3),(1,2,3),(3,5,7) respectively, then the angel between AB and CD, is

Find the angle between the lines whose direction cosines are given by the equation `l+m+n=0` and `l^(2)+m^(2)-n^(2)=0`

ABC is a triangle in a plane with vertices `A(2,3,5),B(-1,3,2)` and `C(lamda,5,mu)`. If the median through A is equally inclined to the coordinate axes, then the value of `lamda^(3)+mu^(3)+5` is