Complete Solutions to Illustrative Example of chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECTS OF CURRENT AND MAGNETISM |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
A current `I = 1.00` A circulates in a round thin-wire loop of radius `R = 100 mm`. Find the magentic induction
(a) at the centre of the loop,
(b) at the point lying on the axis of the loop at a disatnace `x = 100 mm` from its centre.
View SolutionFind the magnetic induction at the point O due to the loop current I in the two cases given below. The shape of the loop are illustrated as
(a) In figure-4.17 (a), the radii A and b, as well as the angle `phi` are known.

(b) In figure 4.17 (b), the radius a and the side b are known.

View SolutionFigure4.18 shows a current carrent carrying wire bent at an angle `alpha`. Find magentic induction at a point P located on the angle bisector at a distance x from the point O at the bend.

View SolutionA current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fiedl induction at the center of polygon due to one side of the polygon is
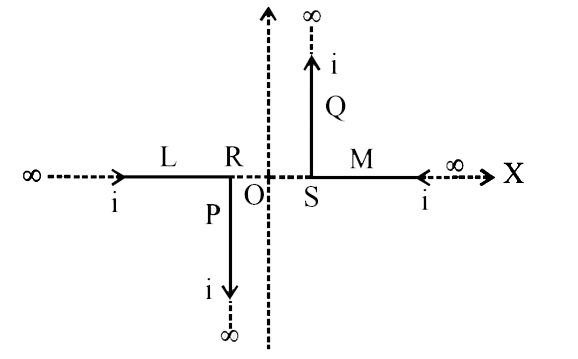
View SolutionA pair of stationary and infintely long bent wires are placed in the ` XY` planes as shown in fig. The wires carry currents of ` I = 10 amperes` each as shown . The segments `P and Q` are parallel to the ` Y-axis` such that ` OS = OR = 0.02 m`. Find the magnitude and direction of the magnetic induction at the origin `O`.
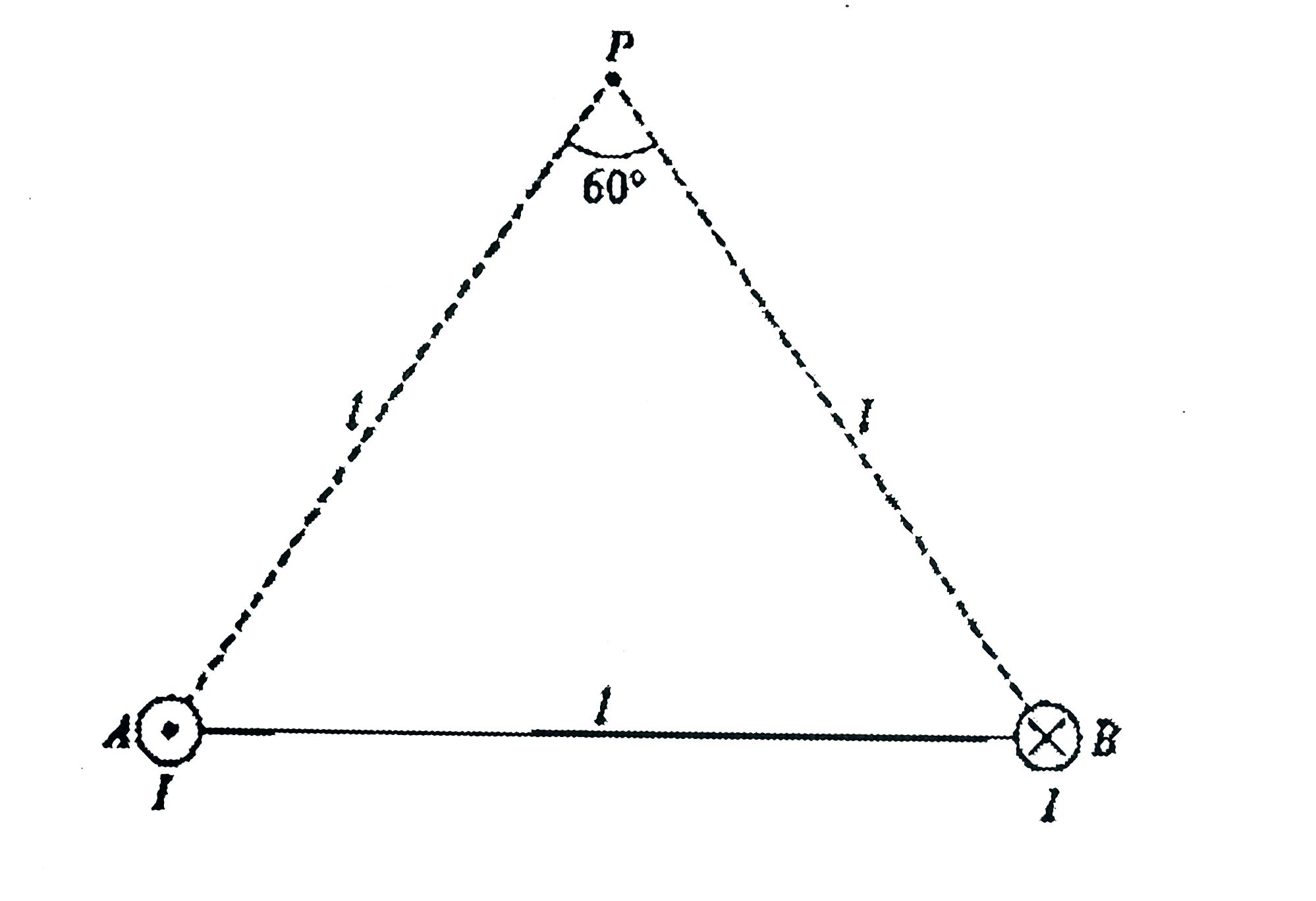
View Solutionfigure 4.22 shows two long wires A and B, each carrying a current I, separated by a distance l and oriented in a plane perpendicular to the plane of paper. The directions of currents are shown in figure. Find the magnetic induction at a point P located at a distance `l` from both wires as shown in figure4.22
View SolutionIn figure-4.24 a current carrying wire configuration is shown with current `l` Find the vector of magnetic induction at origin of co-ordinate system 0.

View Solution`L` is a circular ring made of a uniform wire, currents enters and leaves the ring through straight conductors which, if produces, would have passed through the centre `C` of ring. The magnetic field at `C`
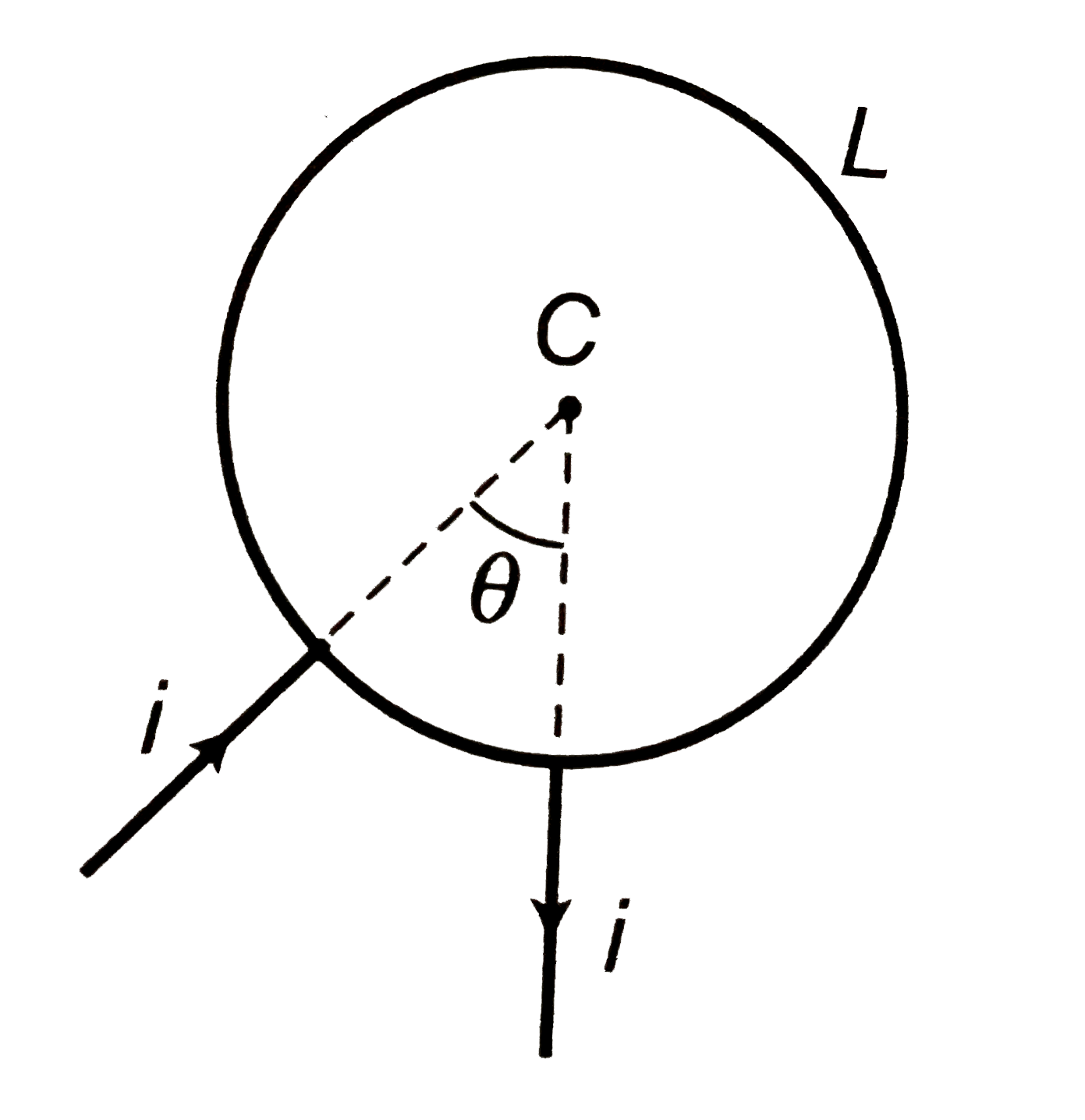
(i) due to the straight conductors is zero
(ii) due to the loop is zero
(iii) due to the loop is proportional to `theta`
(iv) due to loop is proportional to `(pi-theta)`
View SolutionA current `I` flows in a long straight wire with cross-section haviing the form of a thin half-ring of radius `R` (Fig). Find the induction of the magnitude field at the point `O`.

View SolutionA very long straight solenoid has a cross section radis `R` and `n` turns per unit lenghth. A direct current `I `flows throguh the solenoid. Suppose that `x` is the distance from the end of the the solenoid, measured along its axis. Find:
(a) the magnetic induction `B` on the axis as a funciton of `x`, draw an approximate plot of `B` vs ratio `x//R`,
(b) the distance `x_(0)` to the point on the axis at which the value of `B` differs by `eta = 1%` from that in the middle section of the solnoid.
View SolutionA straight long solenoid produces magnetic induction Bat its centre. If it is cut into two equal parts and same number of turns wound on one part in double layer. Calculate magnetic field produced by new solenoid at its centre.
View SolutionA very long straight solenoid carries a current `i`. The cross-sectional area of the solenoid is equal to `S`, the number of turns per unit length is equal to `n`. Find the flux of the vector `B` through the end plane of the solenoid.
View SolutionA non-conducting sphere of radius `R = 50 mm` charged uniformly with surface density `sigma = 10.0 muC//m^(2)` rotates with an angular velocity `omega = 70` rad/s about the asxis passign thorugh its centre. Find the magnetic induction at the centre of the sphere.
View SolutionA coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) `r gt a`, (b) `a lt r lt b` and (c) `b gt r gt c`

View SolutionInside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case `l=0`.

View SolutionIn a long cylindrical wire of radius R, magnetic induction varies with the distance from axis as `B = cr^(alpha)`. Find the function of current density in wire with the distance from axis of wire.
View SolutionFigure-4.76 shows a region of space in which a uniform magnetic induction `B_(0)` is is present between the planes `z = 0` and `z = a`. Using Ampere's law prove that such a field cannot exist between two planes as described here.

View SolutionFigure-4.78 shows a toroidal solenoid whose cross-section is rectangular in shape. Find the magnetic flux through this cross-section if the current through the toroidal winding is I, total number of turns in winding is N, the inside and outside radii of the toroid are a and b respectively and the height of toroid is equal to h.

View SolutionA charge `4 muC` enters in a region of uniform magnetic field with a velocity `(4 hat(i) - 7 hat(j))` m/s experiences a force `(5 hat(i) - C hat(j)) N`. Find the value of C.
View SolutionA charge particle of mass m and charge q is accelerated by a potential difference V volt. It enters in a region of uniform magnetic field Bas shown in figure-4.93. Find the time after which it will come out from the magnetic field.

View SolutionA proton (charge `1.6xx10^(-19) C, mass = 1.67xx10^(-27) kg)` is shot with a speed `8xx10^6 ms^-1` at an angle of `30^@` with the X-axis. A uniform magnetic field `B=0.30 T` exists along the X-axis. Show that path of the proton is a helix. Find the radius and pitch of the helix.
View SolutionAn `alpha-`particle is describing a circle of radius 0.45 m in a field of magnetic induction of 1.2 T. Find its speed, frequency of rotation and kinetic energy. What potential difference will be required to accelerate the particle so as to give this much of the energy to it? The mass of `alpha-`particle is `6.8 xx 10^(-27) kg` and its charge is twice the charge of proton, i.e.,`3.2 xx 10^(-19) C`.
View SolutionA small charged ball having mass m and charge q is suspended from a rigid support by means of an inextensible thread of length l. It is made to rotate on a horizontal circular path in a uniform, time independent magnetic field of induction B which is directed upward. The time period of revolution of the ball is `T_0.` If the thread is always stretched, calculate the radius of circular path on which the ball moves.
View SolutionA particle of mass `m=1.6xx10^-27` kg and charge `q=1.6xx10^-19C` enters a region of uniform magnetic field of stregth `1 T` along the direction shown in figure. The speed of the particle is `10^7 m//s`

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point `F`. Find the distasnce `EF` and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at `E`.
View SolutionIn a right handed coordinate system XY plane is horizontal and Z-axis is vertically npward. A uniform magnetic field exist in space in vertically npward direction with magnetic induction B. A particle with mass m and charge q is projected from the origin of the coordinate system at `t= 0` with a velocity vector given as
`vec(v) = v_(1) hat(i) + v_(2) hat(k)`
Find the velocity vector of the particle after time t.
View SolutionTwo parallel horizontal conductors are suspended by two light vertical threads each 75 cm long. Each conductor has a mass of `40gm`, and when there is no current they are 0.5 cm apart. Equal current in the two wires result in a separation of 1.5 cm. Find the values and directions of currents. Take `g=9.8ms^-2`.
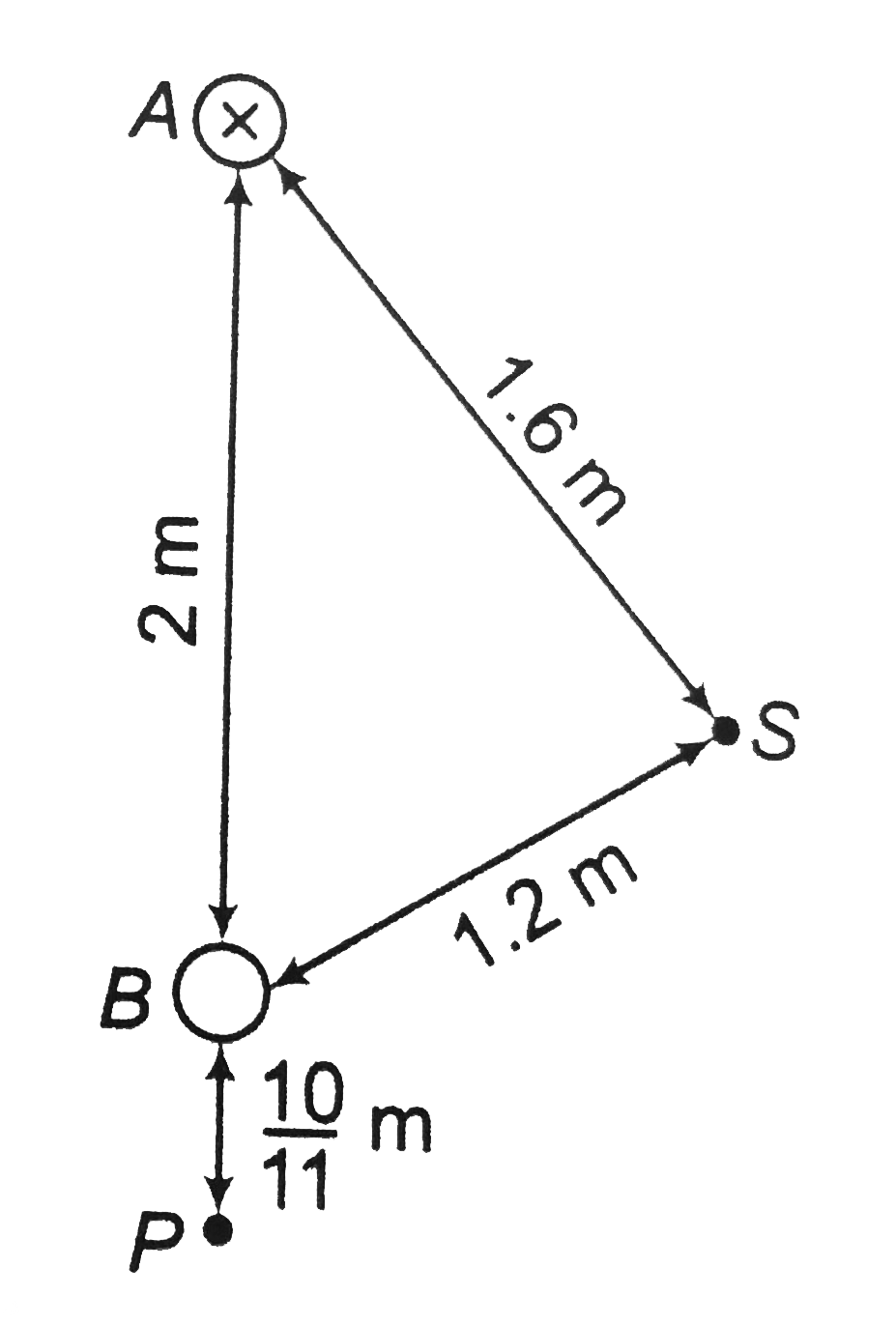
View SolutionTwo long straight parallel wieres are `2m` apart, perpendicular to the plane of the paper. The wire A carries a current of `9.6 A`, directed into the plane of the paper. The wire `B` carries a current such that the magnetic field of induction at the point `P`, at a distance of `10/11` m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont `S`.
c. the force per unit length on the wire `B`.
View SolutionA rod AB of mass m and length `l` is placed on two smooth rails P and Q in a uniform magnetic induction B as shown in figure-4.110. The rails are connected to a current source supplying a constant current J. Find the speed attained by rod AB when it leaves off the other end ofrails oflength L.

View SolutionTwo long parallel wires of negligible resistance are connected at one end to a resistance R and at the other end to a constant voltage source of voltage V. The distance between·the axes of the wires is `eta` times greater than the cross-sectional radiµs of each wire. At what value of resistance R, does the resultant force of interaction between the wires will become zero?
View SolutionA rectangular loop of wire ABCD is oriented with the left corner at the origin, one edge along X-axis and the other edge along Y-axis as shown in the figure-4.113. A magnetic · field exist in space in direction perpendicular to the XYplane as shown and has a magnitude that is given as `B = alpha y` where `alpha` is a constant. Find the total magnetic force on the loop if it carries current i.

View SolutionAn infinte wire place along z-axis has current `I_(1)` in positive z-direction A conducting rod placed in xy plane parallel to y-axis has current `I_(2)` in positive y-direction The ends of the rod subtend `+30^(@)` and `-60^(@)` at the origin with positive x direction The rod is at a distance a from the origin. Find net force on the rod .
View SolutionFigure shows a long straight current carrying wire with a current `I_(1)` and a thin strip of width b and length l placed parallel to it with a current `I_(2)` as shown in figure. Find the magnitude force of interaction between current `I_(1)` and `I_(2)`

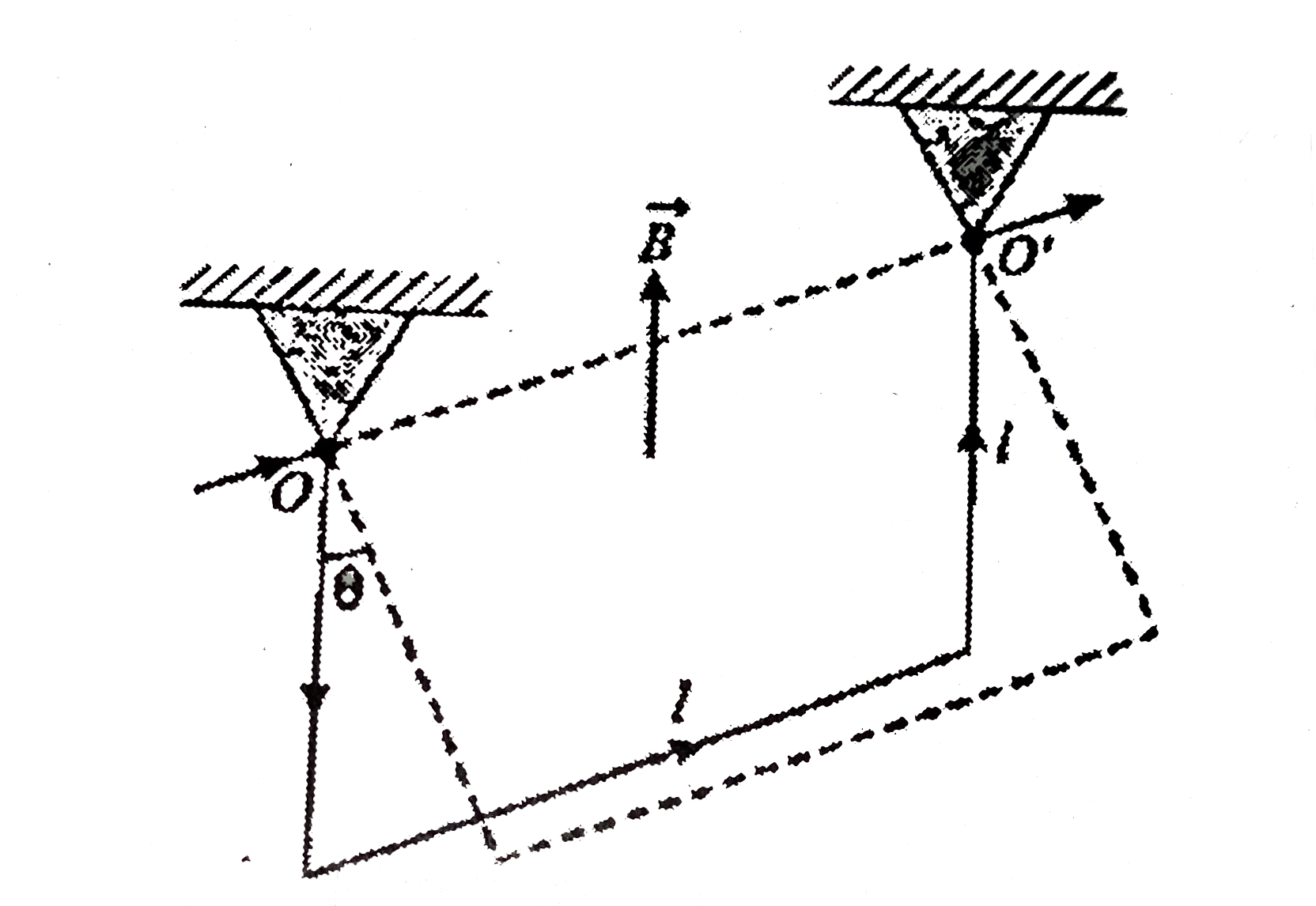
View SolutionA copper wire with density `rho` with cross-sectional area S bent to make three sides of a squae frame which can turn about a horizontal axis OO' as shown in figure. The wire is located in uniform vertical magnetic field. Find the magnetic induction if on passing a current I through the wire the frame deflects by an angle `theta` in its equilibrium position.
View SolutionA proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with `E` and `B` Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
View SolutionA particle of mass `1xx 10^(-26) kg` and charge `+1.6xx 10^(-19) C` travelling with a velocity `1.28xx 10^6 ms^-1` in the `+x` direction enters a region in which uniform electric field E and a uniform magnetic field of induction B are present such that `E_x = E_y = 0, E_z= -102.4 kV m^-1, and B_x = B_z =0, B_y = 8X 10^-2.` The particle enters this region at time `t=0.` Determine the location (x,y,z coordinates) of the particle at `t= 5xx10^-6 s.` If the electric field is switched off at this instant (with the magnetic field present), what will be the position of the particle at `t= 7.45xx10^-6 s` ?
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge `q//m` leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity `v_0`
 `
`
The coordinate `y_n` of the particle when it crosses the y-axis for the `n^(th)` time is
View Solutionan electron beam passes through a magnetic field of magnetic induction `2 xx 10^(-3)T` and an electric field of strength `3.4 xx 10^(4) V//m` both acting simultaneously in mutually perpendicular directions. If the path of electrons remains undeviated, calculate the speed of the electrons. If the electric field is removed, what will be the radius of curvature of the trajectory of the electron path after 2s?
View SolutionThere is a constant homogeneous electric field of `100 Vm^-1` within the region `x=0 and x=0.167 m` pointing in x-direction. There is a constant homogeneous mangetic field B within the region `x=0.167 m and x=0.334 m` pointing in the z-direction. A proton at rest at the origin is released in positive x-direction. Find the minimum strength of the magnetic field B, so that the proton is detected back at `x=0, y=0.167 m.` (mass of proton `= 1.67 xx 10^(-27) kg)`
View SolutionFigure shows a coil of area A and N turns with a current I is placed in a uniform magnetic induction B. Find the work required to pull this coil out from magnetic field.

View SolutionA circular coil of wire 8 cm in diameter has 12 turns and carries a current of 5 A. The coil is in a field where the magnetic induction is 0.6 T.
a. What is the maximum torque on the coil?
b. In what position would the torque be half as great as in (i) ?
View SolutionA square frame carrying a current I is located in the same plane as a long straight wire carrying a current `I_(0)` The frame side has a length a. The axis of the frame passing through the midpoints of the opposite sides is parallel to the wire and is separated from it by the distance which is `eta` times greater than the side of the frame. Find

(a) Force acting on the frame
(b) The mechanical work to be performed in order to turn the frame through `180^(@)` about its axis, with the currents maintained constant.
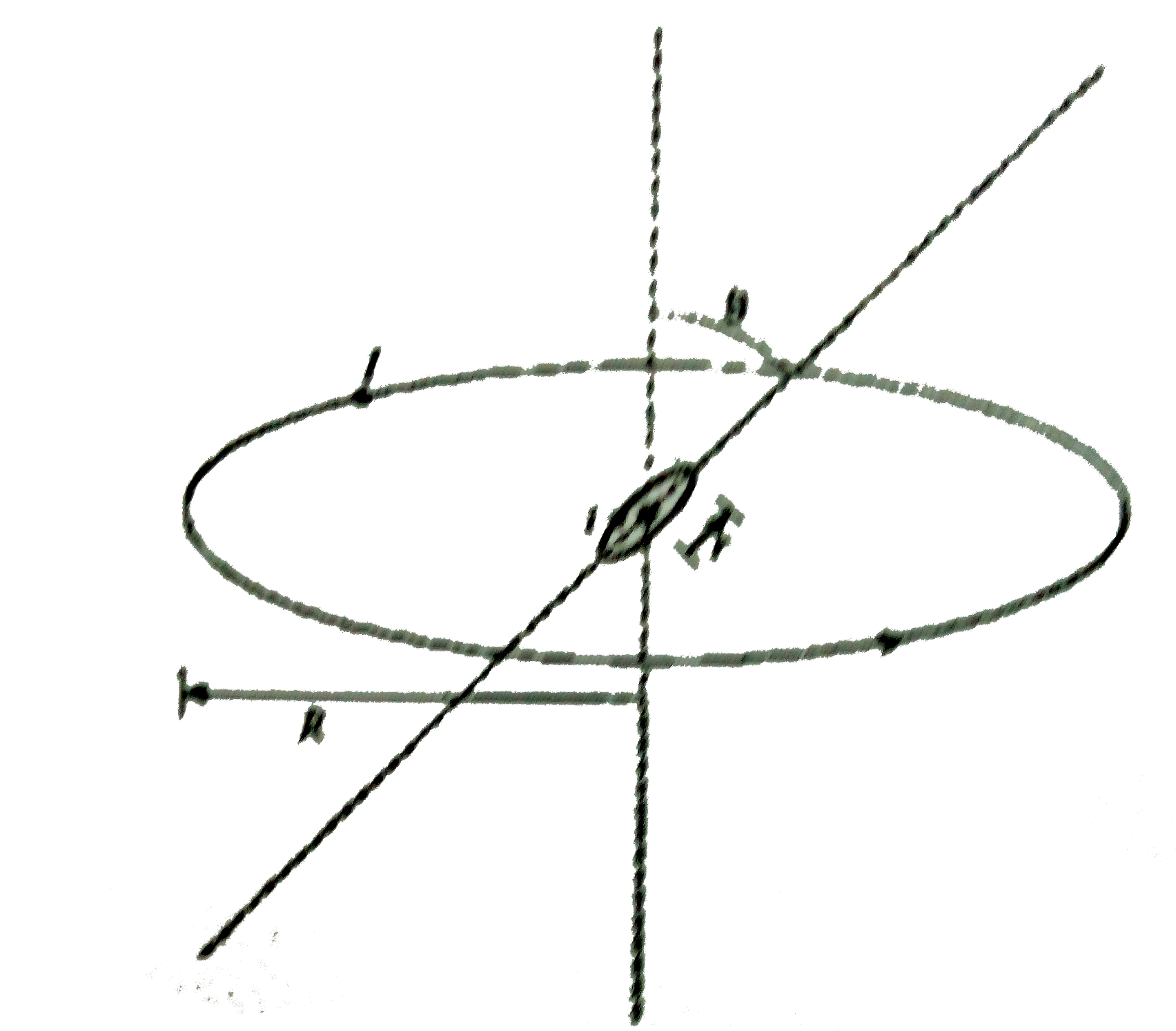
View SolutionFigure shows a larger horizontal coil of radius R carrying a current I. Another small coil of radius `r(r lt lt R)` carrying a current i & N turns is placed at the centre with its plane at an angle `theta` from the axis. Find the torque experienced by the smaller coil in this situation.
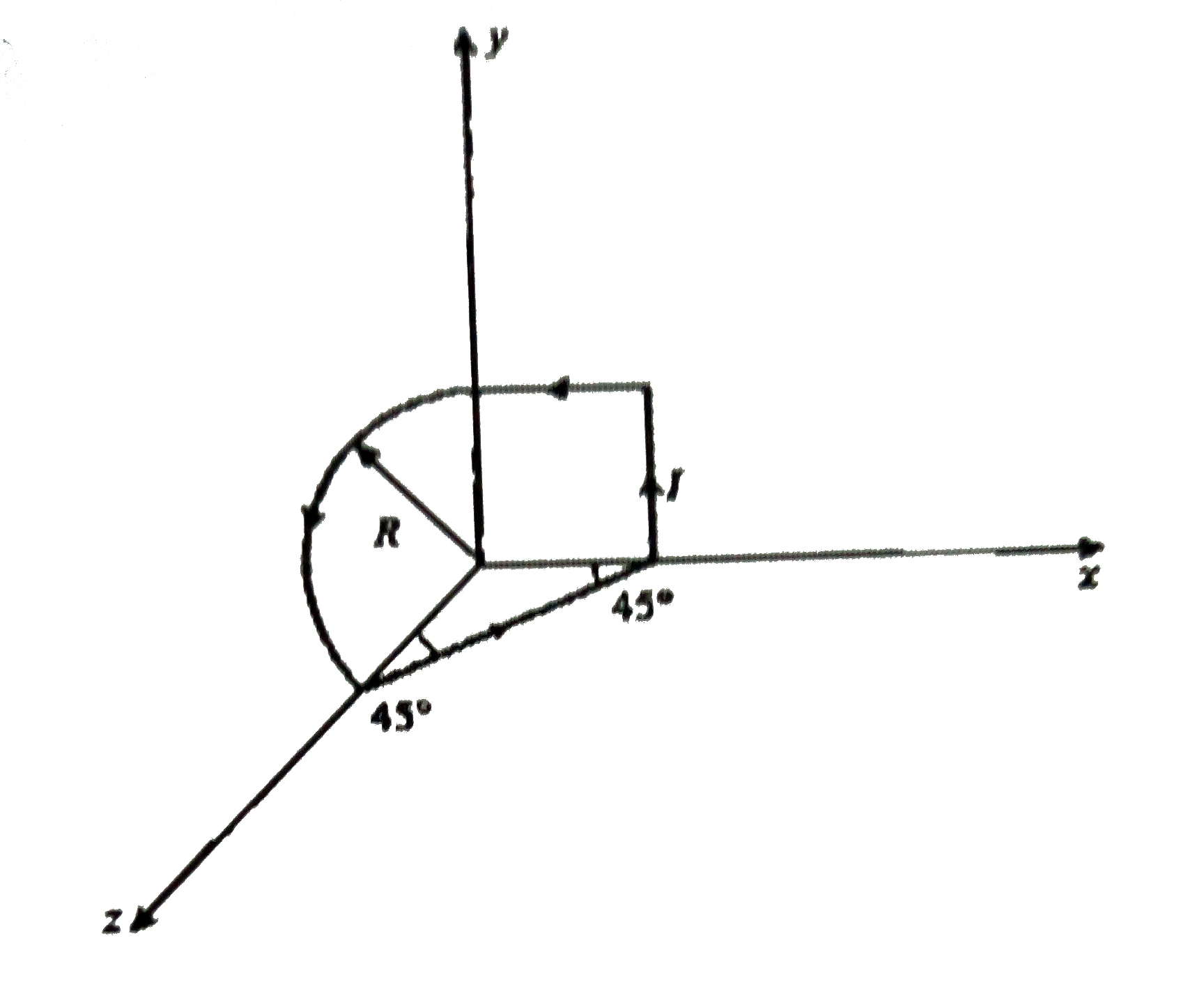
View SolutionFind the magnetic moment of the current carrying loop shown in figure.
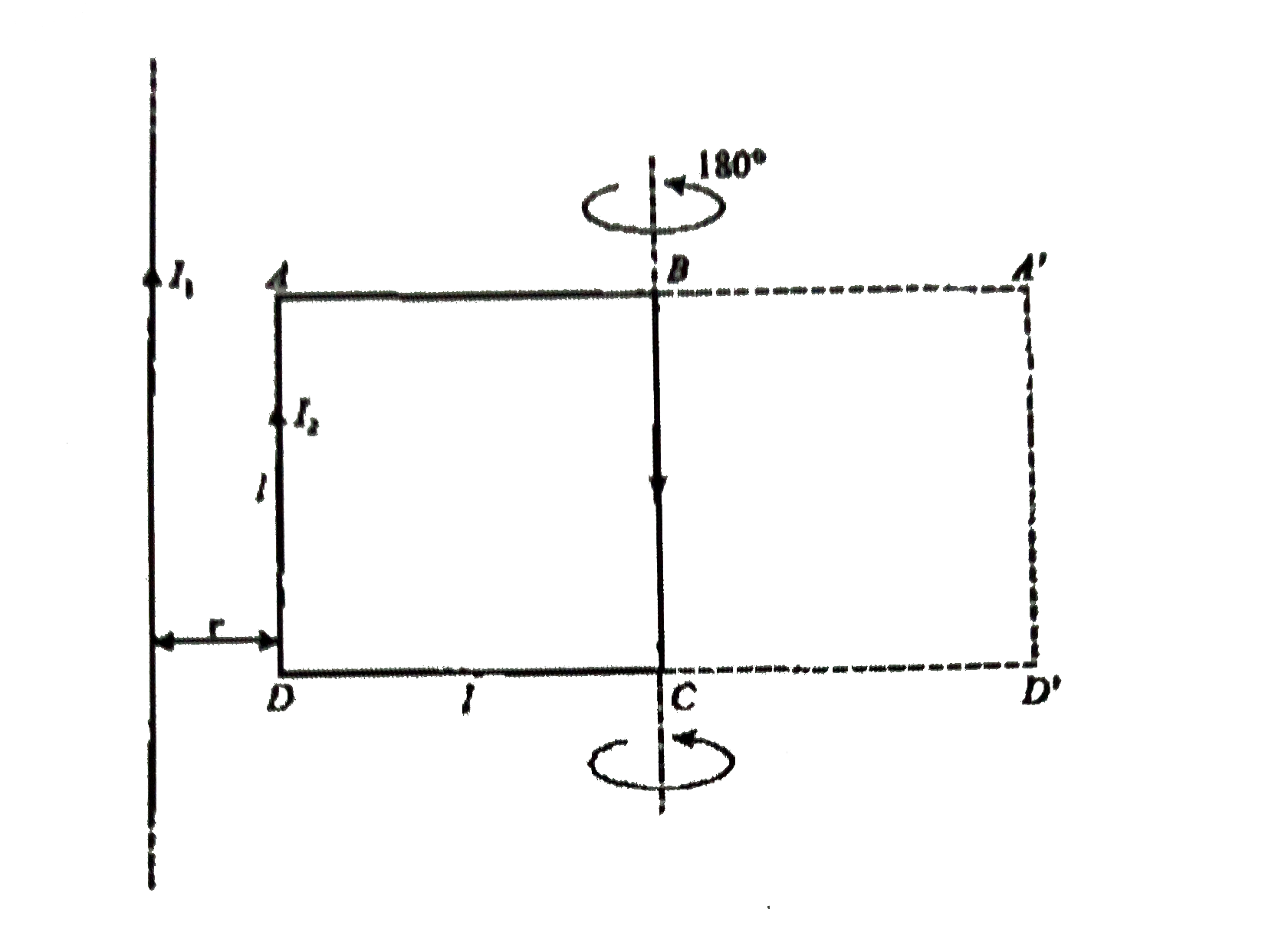
View SolutionA square coil of edge I carrying a current `I_(2)` is placed near to a long straight wire carrying current `I_(1)` as shown in figure. Find work required to rotate the coil ABCD about the axis along edge BC by `180^(@)` to the dotted position A 'BCD' as shown.
View SolutionA rectangular coil of area `5.0 xx 10^(-4)m^(2)` and 60 turns is pivoted about one of its vertical sides. The coil is in a radial horizontal magnetic field of `9 xx 10^(-3) T`. What is the torsional constant of the spring connected to the coil if a current of 0.20mA produces an angular deflection of `180^(@)` ?
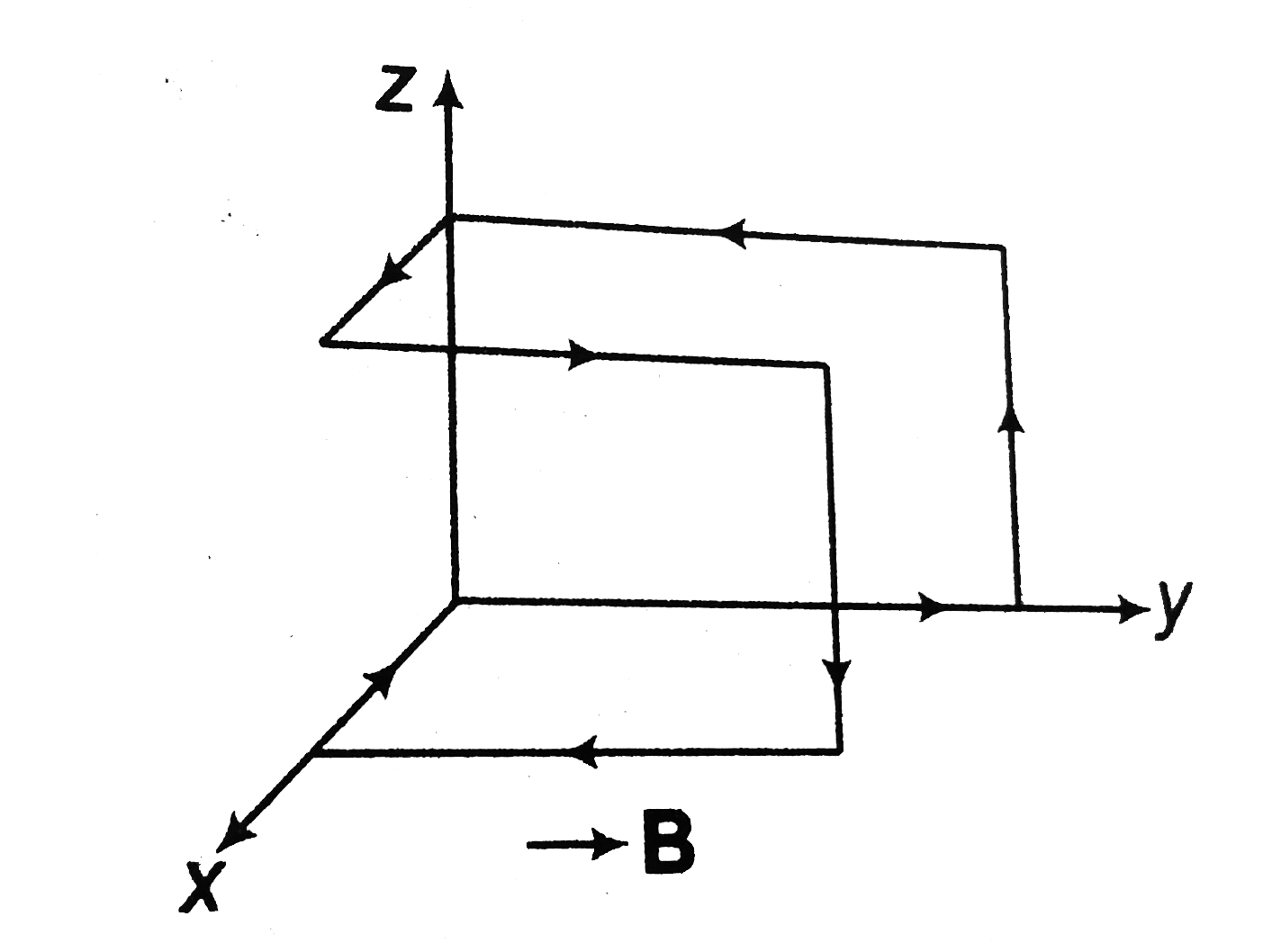
View SolutionGiven figure shows a coil bent with all edges of length `1 m` and carrying a current of `1 A`. There exists in space a uniform magnetic field of `2 T` in positive y-direction. Find the torque on the loop.
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density `sigma`. About its central axis of rotation it rotates at an angular speed `omega`. Find the magnetic moment of disc due to rotation of charges.
View SolutionA flat dielectric disc of radius `R` carries an excess charge on its surface. The surface charge density `sigma`. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity `omega`. Find the toruque on the disc if it is placed in a uniform magnetic field `B` directed perpendicular to the rotation axis.
View SolutionA sphere of radius R, uniformly charged with the surface charge density `sigma` rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.
View SolutionWhat pressure does the lateral surface of a long straight solenoid with n turns per unit length experience when a current I flows through it.
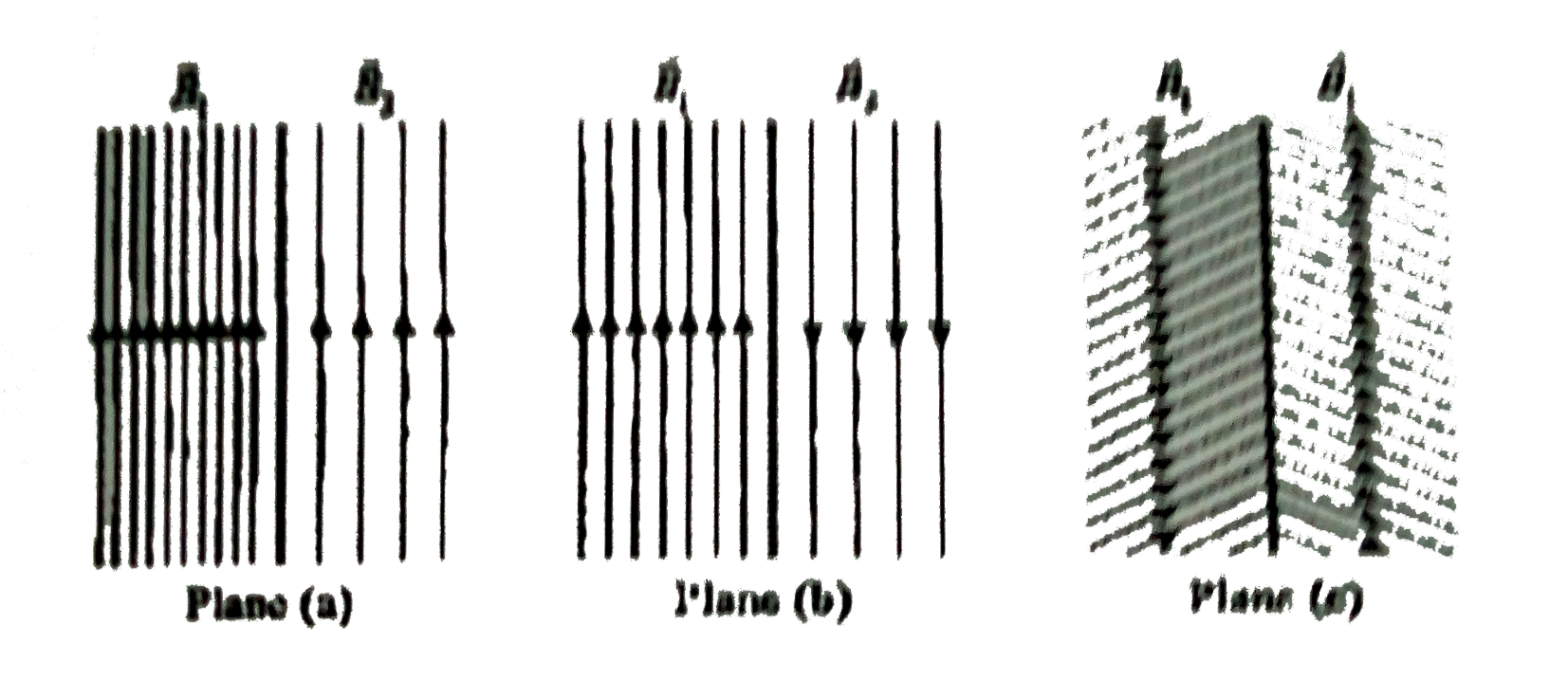
View SolutionA conducting current-carrying plane is placed in an external uniform magnetic field. As a result, the magnetic induction becomes equal to `B_(1)` on one side of the plane and equal to `B_(2)` on the other side. Find the magnetic force acting per unit area of the plane in the cases illustrated in the figure.
View SolutionA bar magnet is 0.1 m long and its pole strength is 12 Am. Find the magnetic induction at a point on its axis at a distance of 0.2 m from its centre.
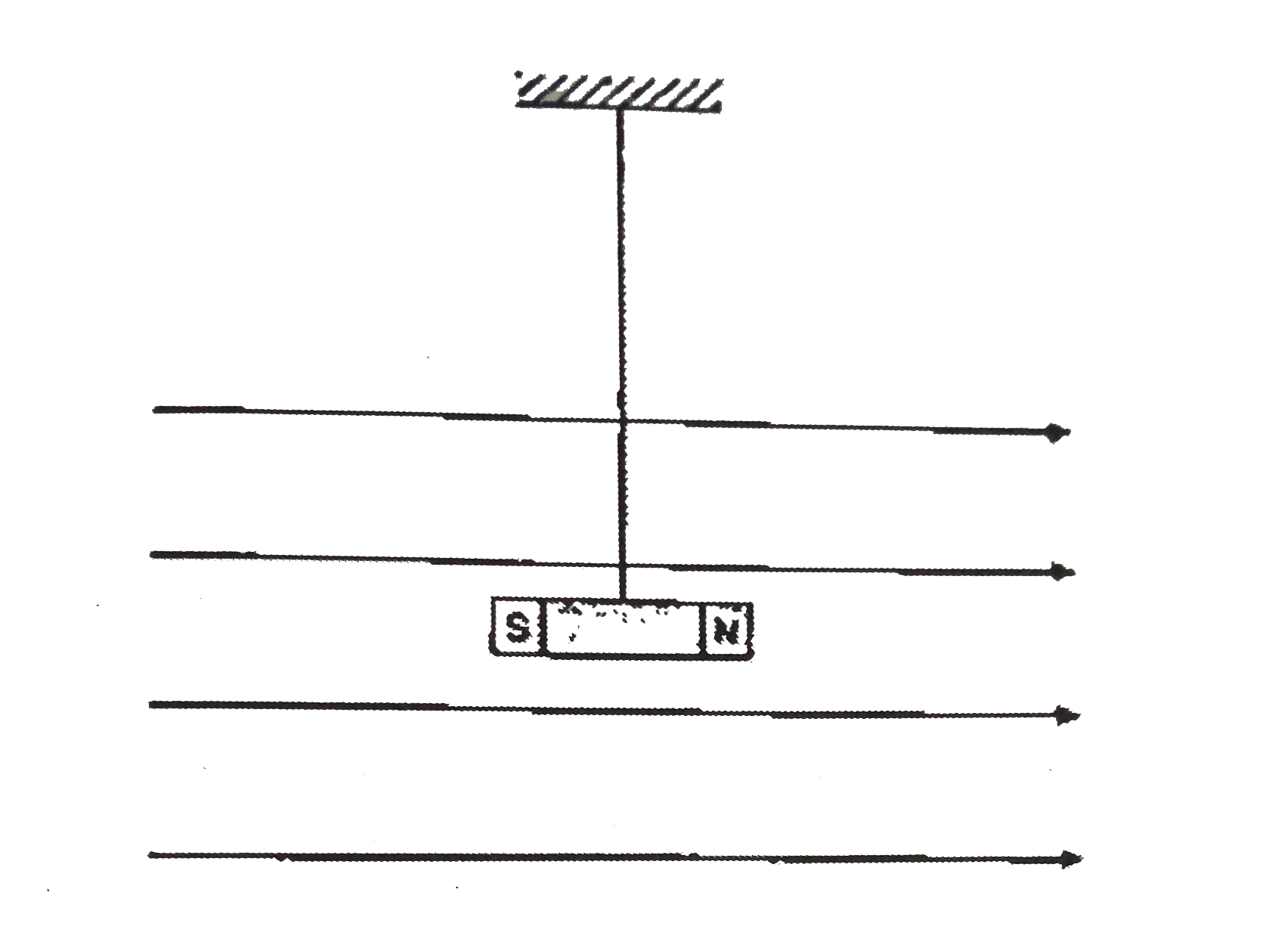
View SolutionA magnetic dipole of magnetic moment M is suspended by a string in a uniform horizontal magnetic field as showo in figure. If in horizontal plane this dipole is slightly tilted and released, show that it will execute simple harmonic motion and find its oscillation period. Consider the dipole as a uniform rod of mass m and length I.
View SolutionA small magnet of magnetic moment `pixx10^(-3) Am^(2)` is placed on the Y-axis at a distance of 0.1 from the origin with its axis parallel to the X-axix. A coil have 169 turns and radius 0.05 m is placed on the X-axis at a distance of 0.12 m from the origin with the axis of the coil coinciding with the X-axis. Find the magnitude and direction of the current in the coil for a compass needle placed at the origin, to point in the north-south direction.
View SolutionCenters of two similar coils P and Q having same number of turns are located at the coordinates (0.4,0) and (0,0.3) such that the plane of coils are perpendicular to X-and Y-axis respectively. The areas of cross section of coils P and Q are in the ration `4:3` Coil P has 16 A current in clockwise direction and coil Q has `9sqrt3A` current in anticlockwise direction as seen from the origin. A small compass needle is placed at the origin. Find the deflection in the needle, assuming the earth's magnetic field negligible and the radii of the coils very small compared to their distances from the origin.
View SolutionA magnetic dipole with a dipole moment of magnitude `0.020 J/T` is released from rest in a uniform form magnetic field of magnitude `52 mT`. The rotation of the dipole due to the magnetic force on it is unimpeded. When the dipole rotates through the orientations where its dipole moment is aligned with the magnetic field, its kinetic energy is `0.80 mJ`.
(a) What is the initial angle between the dipole moment and the magnetic field?
(b) What is the angle when the dipole is next (momentarily) at rest?
View SolutionFigure shows two small bar magnets having dipole moments `M_(1)` and `M_(2)` placed at separation r. Find the magnetic interaction energy of this system of dipoles for `d lt lt r`.

View SolutionAt a point on earth surface horizontal component of earth's magnetic field is `40 mu T` and dip angle is `30^(@)`. Find the total magnetic field of earth at this point.
View SolutionThe radius of tangent galvanometer coil is 16 cm. Find the number of turn in its coil if a current of 40 mA is required to produce a deflection of `30^(@)` in it from magnetic meridian. Horizontal component of earth's magnetic field is `36 xx 10^(-6)T`.
View SolutionIn the magnetic meridian of a certain place at the center of the coil ofa tangent galvanometer, the horizontal component of earth's magnetic field is 0.26G and the dip angle is `60^(@)`. Find:
(a) Vertical component of earth's magnetic field
(b) The net magnetic field at this place.
(c) If a current is passed in tangent galvanometer, its coil produces a magnetic induction `3.47 xx 10^(-3)T`. Calculate the defleciton in compass needle of tangent galvanometer.
View Solution
Illustrative Example questions and complete solutions for chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12