Complete Solutions to Numerical MCQ of chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECTS OF CURRENT AND MAGNETISM |
| PHYSICS GALAXY | Numerical MCQ |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
An infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto `+oo`. The magnitude of magnetic field strength at point (a,0) is

View SolutionA conducting rod of mass `50 gm` and length `10 cm` can slide without friction on two long, horizontal rails. A uniform magnetic field of magnitude `5 mT` exists in the region as shown. A source `S` is used to maintain a constant current `2 A` through the rod. If motion of the rod starts from the rest, its speed after `10 s` from the start of the motion will be
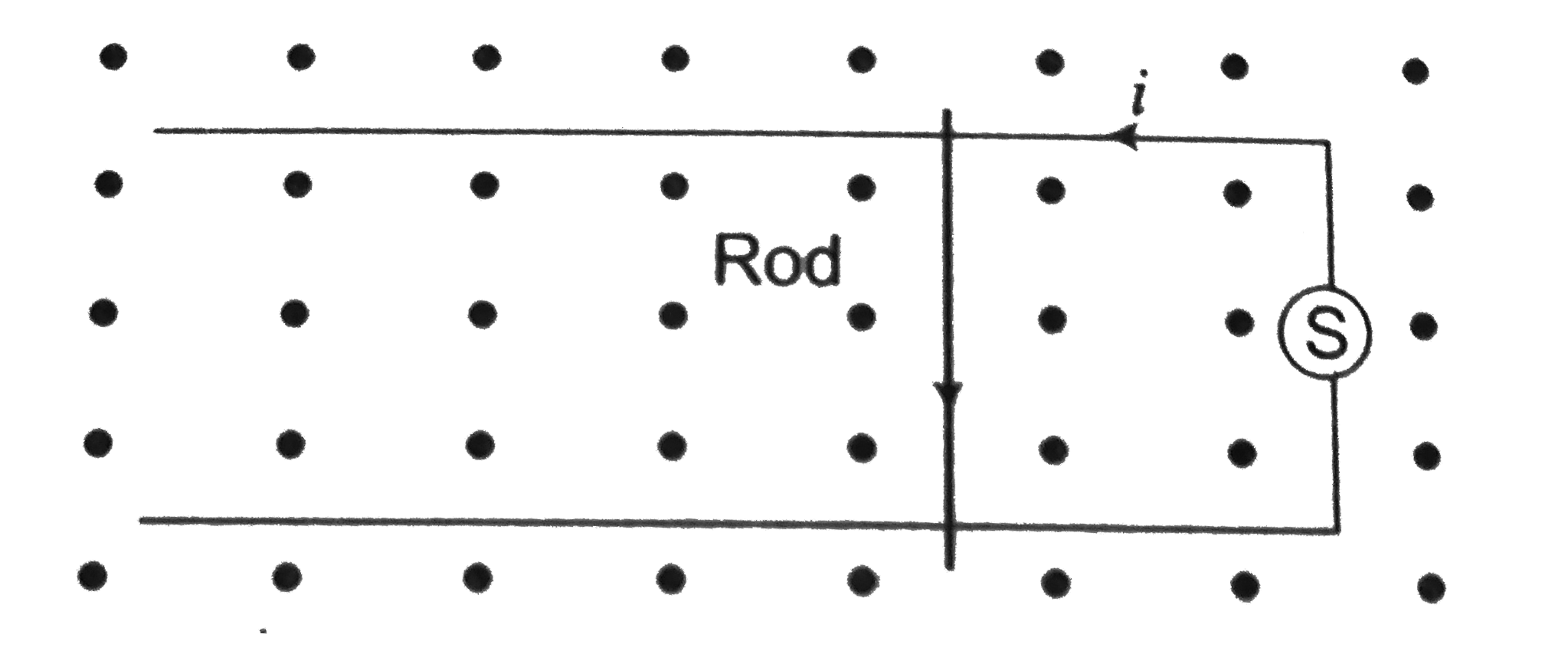
View Solution
A long stragith wire, carrying a current l is bent at its mid point to form an angle `60^(0)`. AT a point P, distance R from the point of bending the magnetic field is
View SolutionTwo infinitely long linear conductors are arranged perpendicular to each other and are in mutually perpendicular planes as shown in Fig. If `I_1=2A` along the y-axis, `I_2=3A`, along -ve z-axis and AP=AB=1cm, the value of magnetic field strength `vecB` at P is

View SolutionA particle of mass m and charge q is thrown from origin at t=0 with velocity `2hati+3hatj+4hatk` units in a region with uniform magnetic field `vecB=2hati` units. After time `t=pim//qB`, an electric field `vecE` is switched on such that particle moves on a straight line with constnat speed `vecE` may be:
View SolutionIf the magnetic induction at a point on the axis of current coil is half of that at the centre of the coil, then the distance of that point from the centre of the coil is :
View SolutionA current carrying circular coil of single tum of mass mis hanged by two ideal strings as shown in the figure-4.214. A constant magnetic field `vecV` is set up in the horizontal direction in the region. The ratio of tension `(T_(1)//T_(2))` in the string will be: [Take `pi BIR=(mg)/(4)` and `theta=45^(@)` in the figure shown]
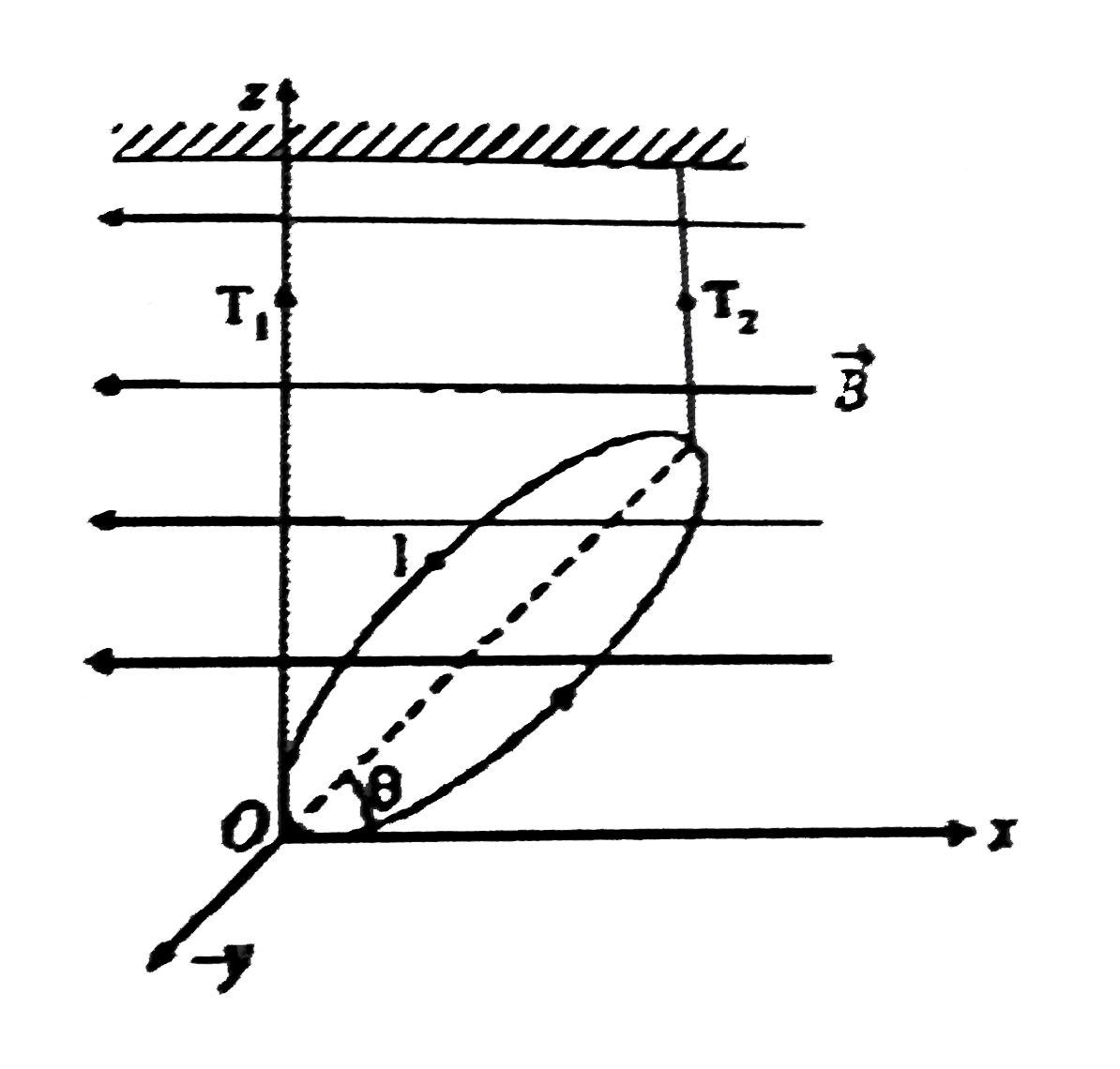
View SolutionA helium nucleus is moving in a circular path of radius 0.8m. If it takes 2s to complete one revolution. Find out magnetic field produced at the centre of the circle:
View SolutionA conductor of length l is placed in E - W direction on a plane. Earth's horizontal magnetic field is B. The amount of charge passed through it when it is found to jump to a hight h is

View SolutionAn `alpha` is moving along a circle of radius R with a constant angular velocity `omega`. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by the `alpha`-particle. If the minimum time interval between two successive time at which A records zero magnetic field is t, the angular speed `omega`, in terms of t, is
View SolutionConsider six wires coming into or out of the page, all with the same current. Rank the line integral of the magnetic field (from most positive to most negative) taken counterclockwise around each loop shown

View SolutionA current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and `2r` . Each segment of arc subtends equal angle at the common centre `P` The magnetic field produced by current path at point `P` is
 .
.
View SolutionA charged particle of specific charge (Charge/mass) `alpha` is released from origin at time t=0 with a velocity given as
`vecv=v_(0)(hati+hatj)`
The magnetic field in region is uniform with magnetic induction `vecB=B_(0)hati`. Coordinates of the particle at time `t=(pi)/(B_(0)alpha)` are:
View SolutionThe configuration of some current carrying wires is shown in figure-4.217. All straight wires are very long. Both AB and CD are arcs of the same circle, both subtending right angles at the centre 0. The magnetic field at O is:
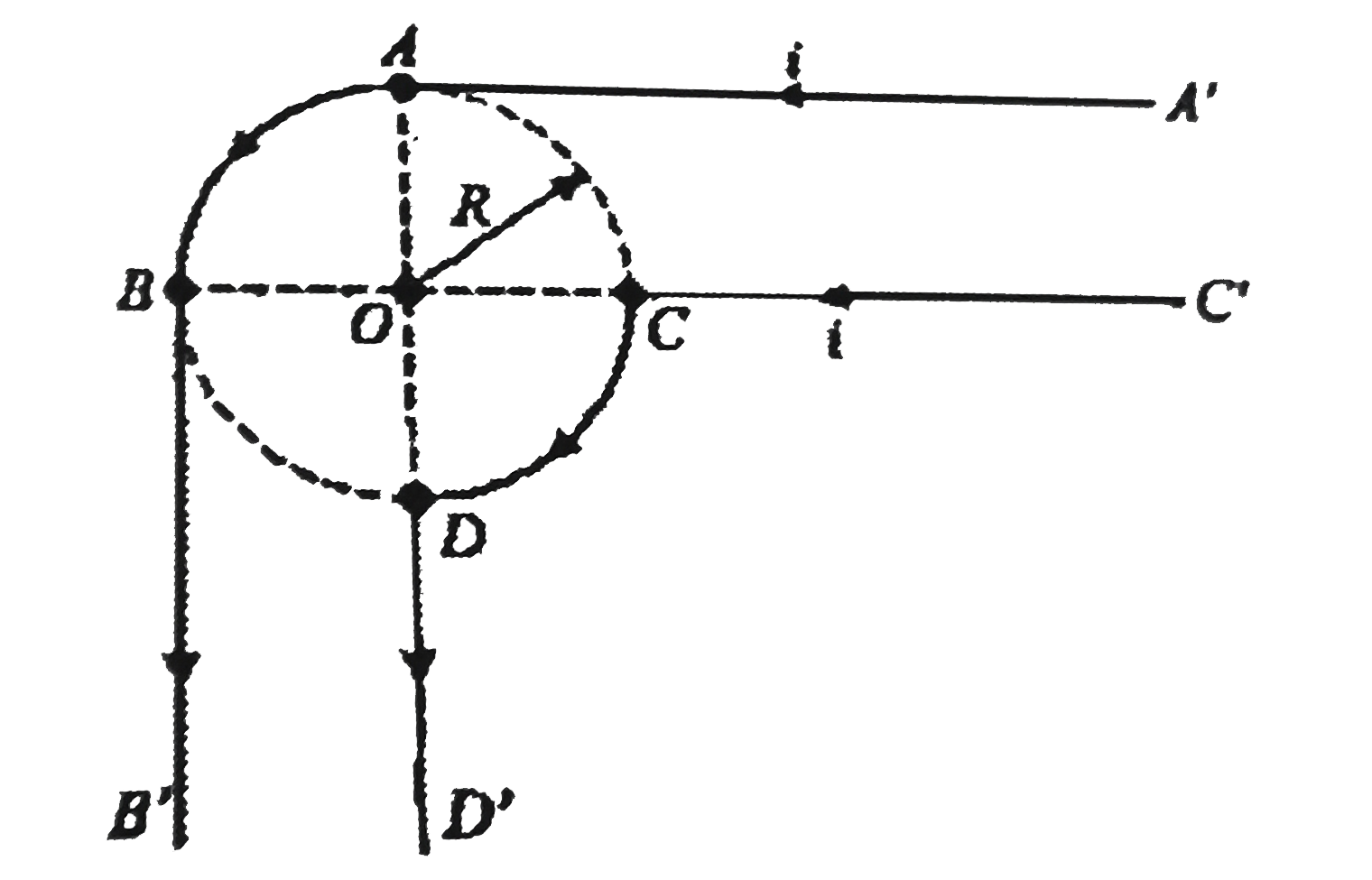
View SolutionA current i in a circular loop of radius b produces a magnetic field. At a fixed point fur from the loop on its axis the magnetic field is proportional to which of the following combinations of i and b ?
View SolutionTwo long conductors are arranged as shown above to form overlapping cylinders, each of raidus r, whose centers are separated by a distance d Current of density j flows into the plane of the page along the shaded part of one condutor and an equal current flows out of the plane of the page along the shaded portion of the other, as shown. What are the magnitude and direction of the magnetic field at point b`A` ?
 .
.
View SolutionThe radius of a coil of wire with N turns is 0.22m, and 3.5Acurrent flows clockwise in the coil as shown.Along straight wire carrying a current 54A toward the left is located 0.05 m from the edge of the coil. The magnetic field at the centre of the coil is zero tesla. The number of turns Nin the coil are:

View SolutionTwo protons parallel to each other, keeping distane r between them, both moving with same velocity `vecV` Then the ratio of the electric is magnetic force of interaction between them is .
View SolutionA neutral atom of atomic mass number I 00 which is stationary at the origin in gravity free space emits an a-particle (A) in z-direction. The product ion is P. A uniform magnetic field exists in the x-direction. Disregard the electromagnetic interaction between A and P. If the angle ofrotation of A after which A and P will meet for the first time is `(npi)/(25)` radians, what is the value of n?
View SolutionIf the ratio of time periods of circular motion of two charged particles in magnetic field in `1//2`, then the ratio of their kinetic energies must be :
View SolutionIn the figure shown, a charged particle of mass 2 g and charge `5 mu C` enters a circular region of radius `10 cm`, in which there is a uniform magnetic field of strength 4 T and directed perpendicular to the plane of circular region in the figure. If the particle velocity vector rotates through `90^(@)` angle in passing through this region then its speed is :
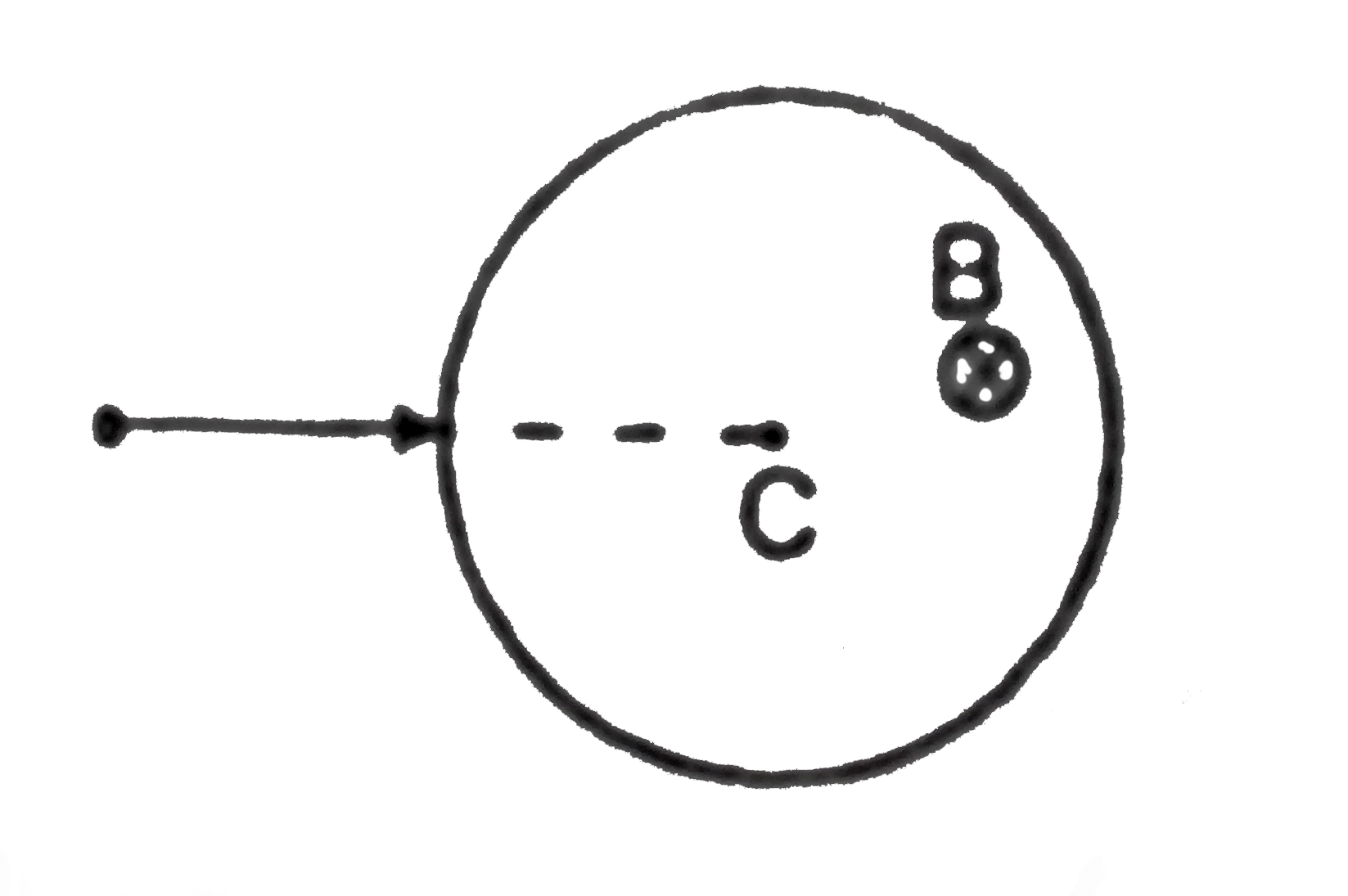
View SolutionThe magnetic field shown in the figure consists of two uniform regions. The width of the first part is 5cm and the magnetic induction here is `0.001` T. The width of the other part is also 5cm, with the direction of the induction being opposite in direction and `0.002` T in magnitude. What should be the minimum speed of the electron arriving from the direction indicated in the figure so that it can pass through the magnetic field? Mass of electron `=9xx10^(-31)`kg
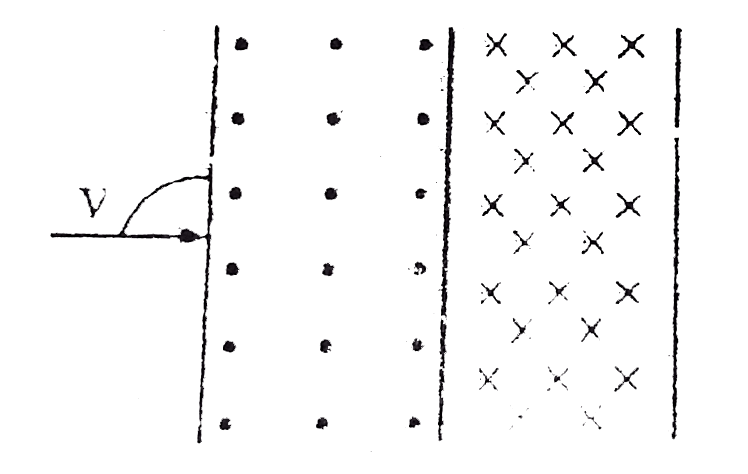
View SolutionIn the figure -4.222 the force on the wire ABC in the given uniform magnetic field of magnetic induction 2T is:
View SolutionA uniform magnetic field exist in a region which forms an equilateral triangle of side a. The magnetic field is perpendicular to the plane of the triangle . A charged q enters into this magnetic field perpendicular to a side with speed v. The charge enters from midpoint and leaves the field from midpoint of other side. Magnetic induction in the triangles is
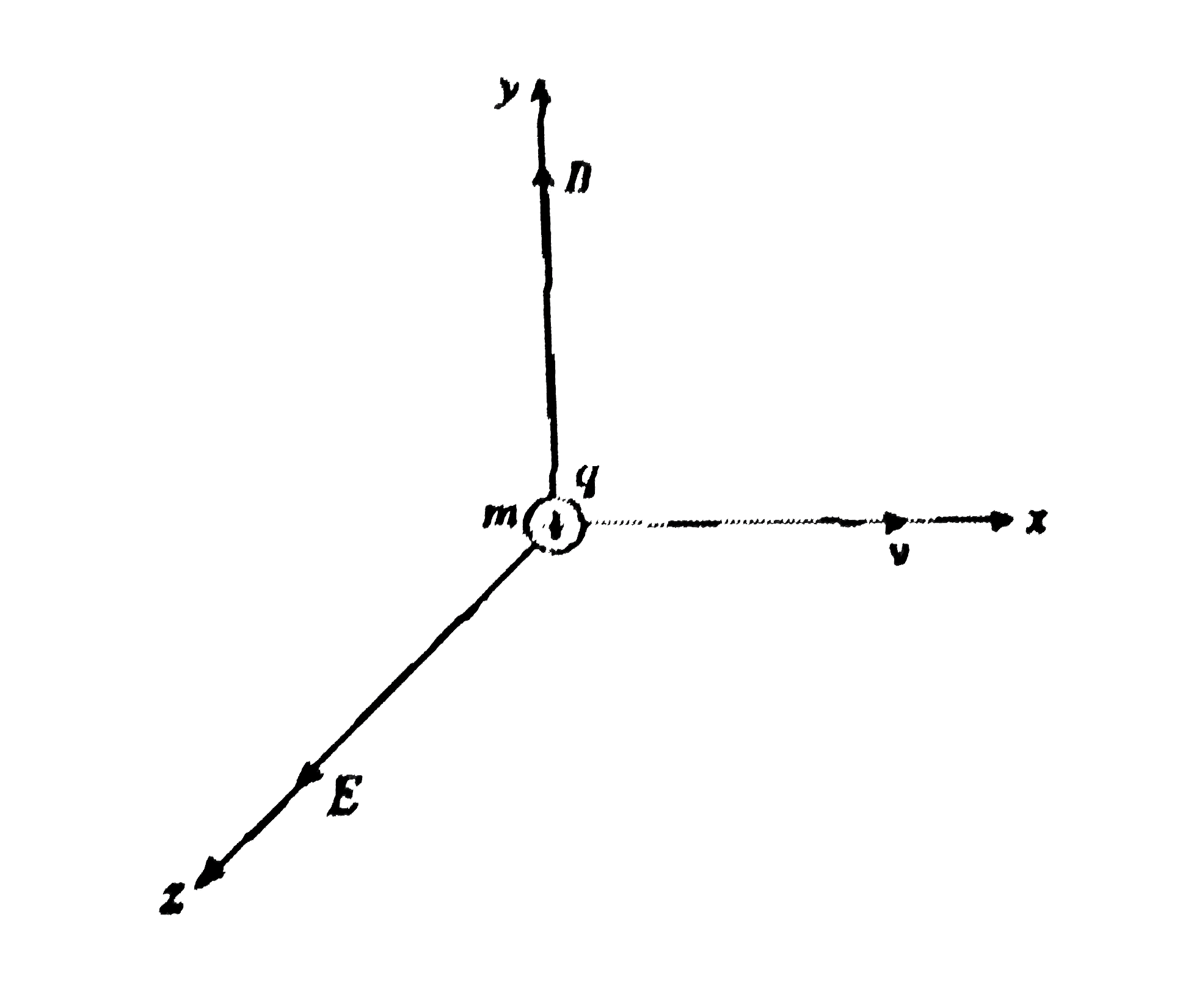
View SolutionA charge particle of charge q, mass m is projected with a velocity `vecv=vhati` in a region of space where electric field strength `vecE=Ehatk` and magnetic induction `vecB=Bhatj` are present. The acceleration of the particle is:
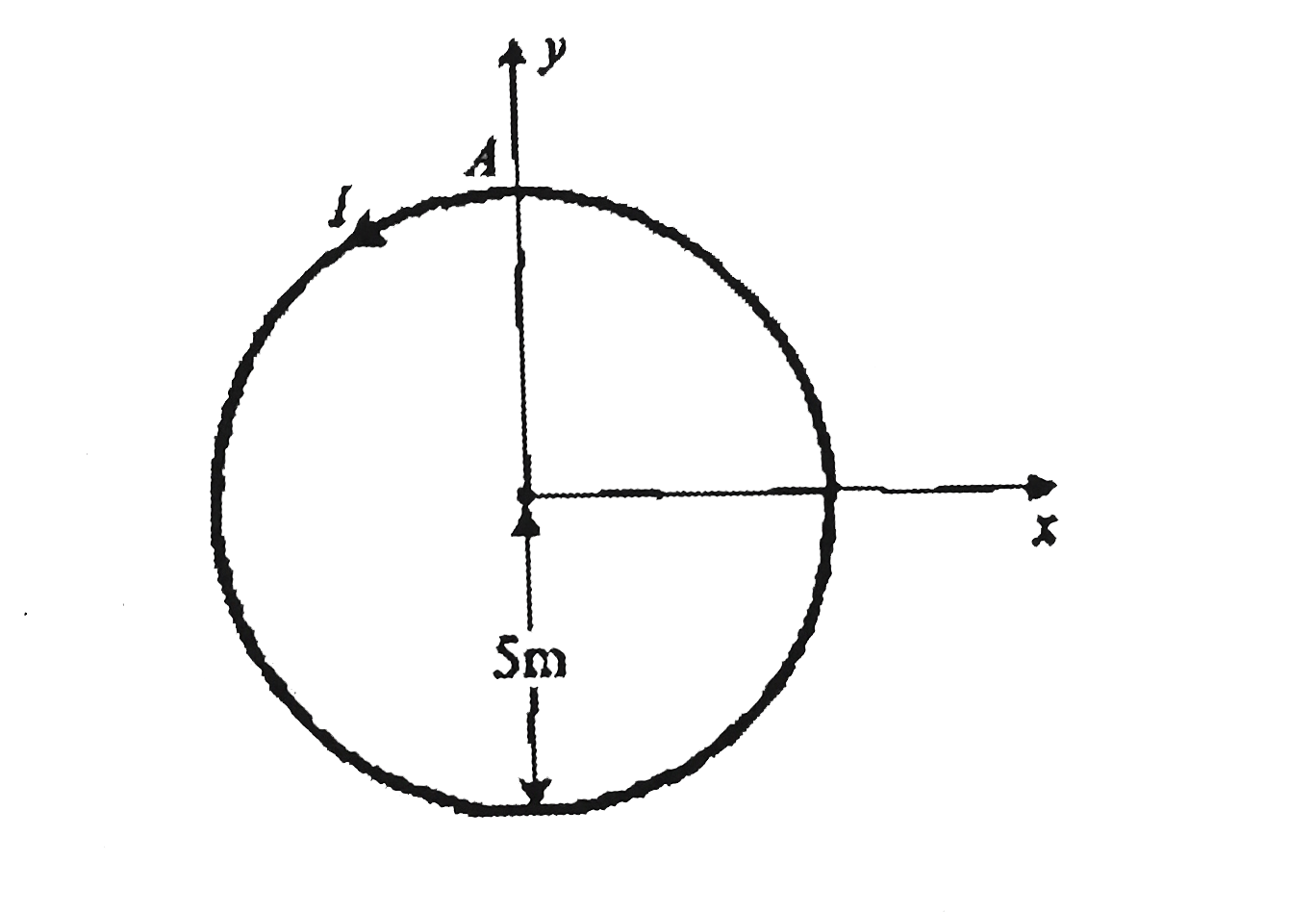
View SolutionA ring of raidus 5m is lying in the x-y plane is carrying current of 1A in anti-clockwise sence. If uniform magnetic field of magnetic induction `vecB=3hati+4hatj` is switched on in space, then the co-ordinates of point about which the loop will have a tendency to lift up is:
View SolutionAn electron is shot into one end of a solenoid.As it enters the uniform magnetic field within the solenoid, its speed is `800 m//s` and its velocity vector makes an angle of `30^(@)` with the central axis of the solenoid.The solenoid carries `4.0 A` current and has `8000` turn along its length.Find number of revolutions made by the electron within the solenoid by the time it emerges from the solenoid's opposite end. (Use charge of mass ratio `e/m` for electron `=sqrt3xx10^(11) C//kg`)Fill your answer in multiple of `10^(3)` (neglect end effect)
View SolutionTwo identical wires each of length L are bent to form a circular loop and a square loop. If the same current i flows in the two wires, then the ratio of the magnetic inductions at the centre of the circular and square loops is :
View SolutionIn a gravity free space, a smooth insulating ring of radius R, with a bead having charge q is placed horizontally in a uniform magnetic field of induction `B_(0)` and perpendiuclar to the plane of ring. Starting from t=0, the magnetic field is varying with time as B(l)=B_(0)+at`, where `alpha` is a positive constant. The contact force between the ring and bead as a function of time is:
View SolutionA bar magnet is held perpendicular to a uniform magnetic field. If the couple acting on the magnet is to be halved by rotating it, then the angle by which it is to be rotated is
View SolutionLet `B_(P)` and `B_(Q)` be the magnetic field produced by the wire P and Q which are placed symmetrically in a rectangular loop ABCD as shown in figure. Current in wire P is I directed inward and in Q is 2I directed outwards.
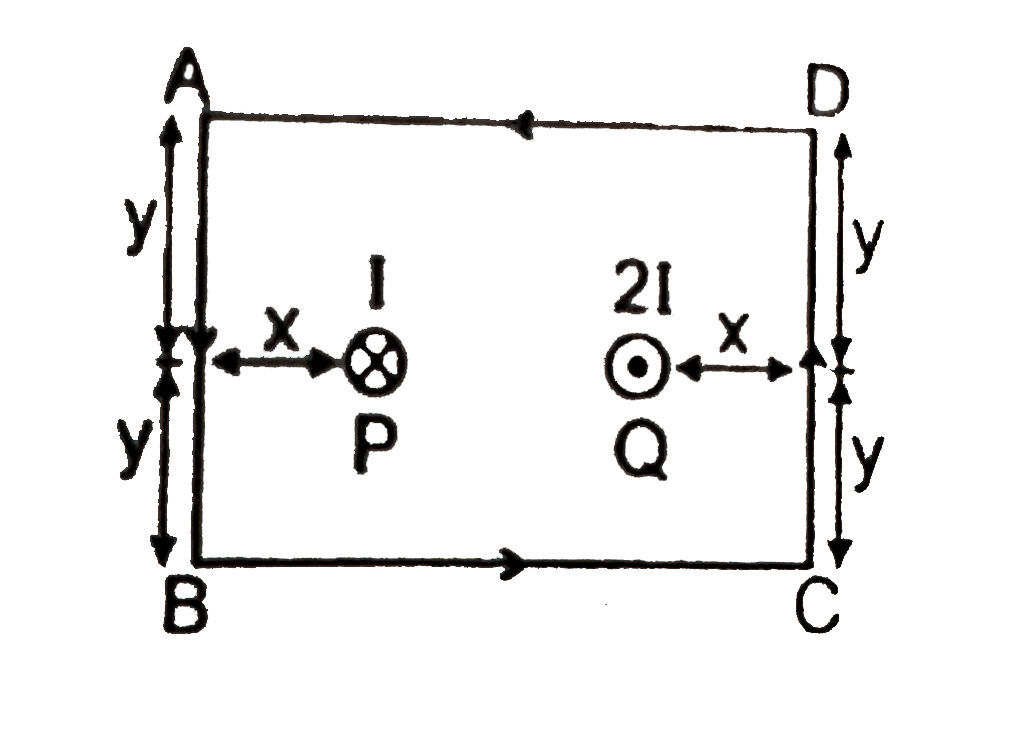
If `int_(A)^(B)vecB_(Q).vecdl=wmu_(0) "tesla meter",int_(D)^(B)vecB_(P).vecdl=-2mu_(0)` tesla meter
`&` `int_(A)^(B)vecB_(P)vecdl=-mu_(0)` tesla meter
the value of 1 will be:
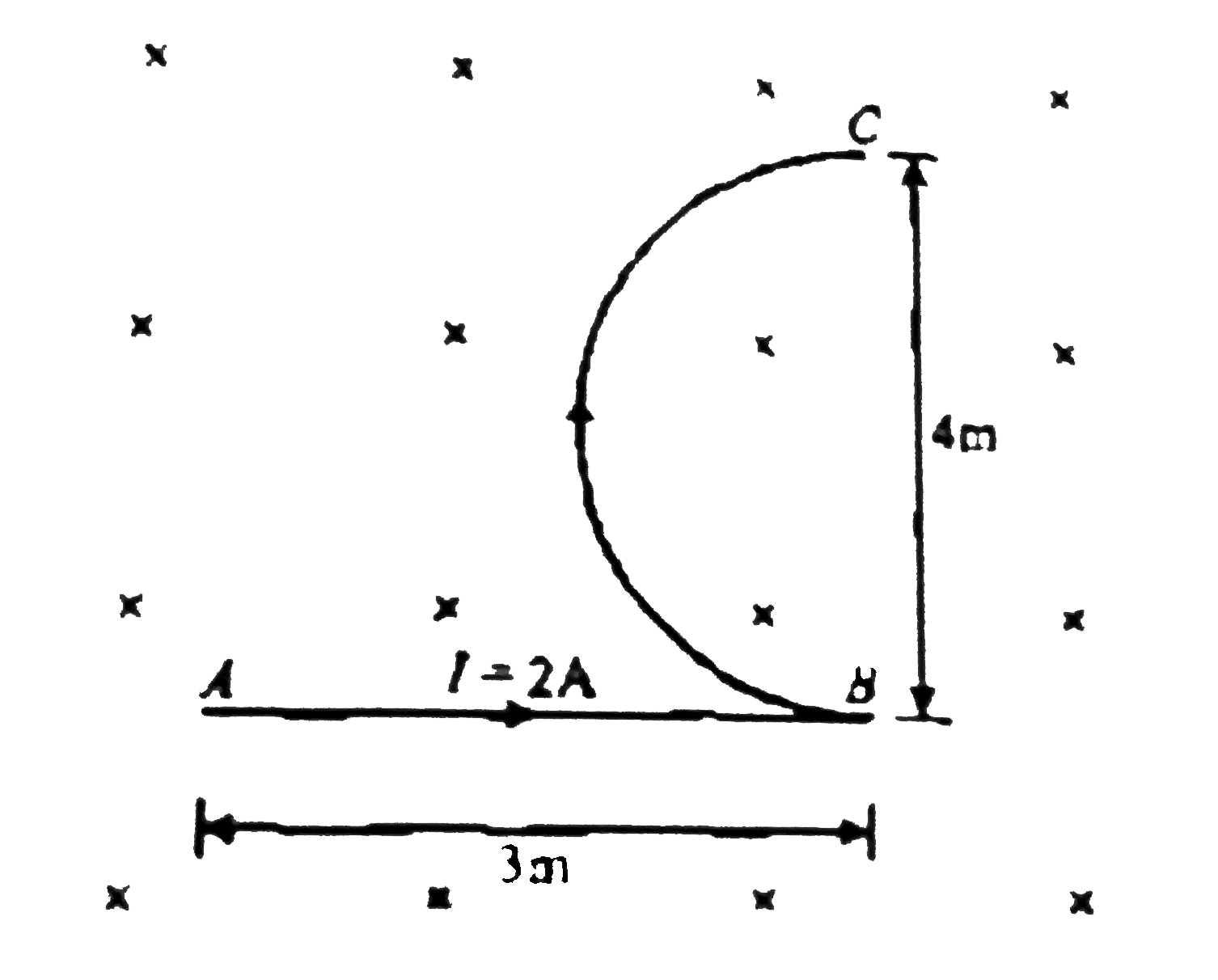
View SolutionA wire carrying a current of 3A is bent in the form of a parabola `y^(2)=4-x` as shown in figure-4.226, where x and y are in metre. The wire is placed in a uniform magnetic field `vecB=5hatkT`. The force acting on the wire is:

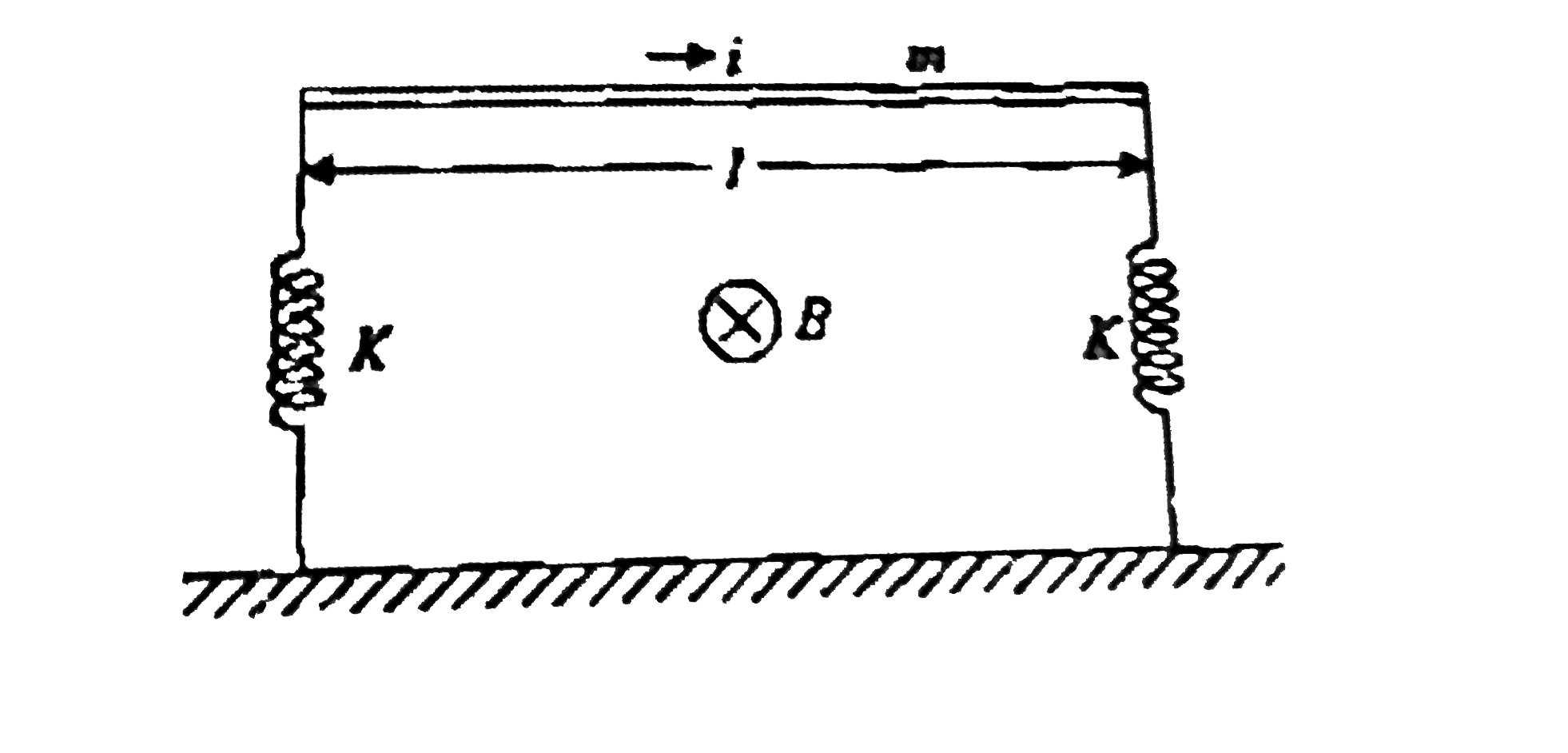
View SolutionA horizontal metallic rod of mass `m` and length `l` is supported by two vertical identical springs of spring constant `k` each and natral length `i_(0)` A current `l` is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionA dip circle is adjusted so that its needle moves freely in the magnetic meridian. In this position, the angle of dip ia `40^(@)`. Now the dip circle is rotated so that the plane in which the needle moves makes an angle of `30^(@)` with the magnetic meridian. In this position the needle will dip by an angle
View SolutionAn infinite current carrying conductor is bent into three segments as shown in the figure-4.228. if it carries current i, the m agnetic field at the origin is found to be `(mu_(o)l)/(rpia)(sqrt(x-1)hatj+hatk)`. The value of x is:

View SolutionA charged particle moving along +ve x-direction with a velocity v enters a region where there is a uniform magnetic field `B_0(-hat k), from x=0 to x=d.` The particle gets deflected at an angle `theta` from its initial path. The specific charge of the particle is

View SolutionIf the magnetic field at P can be written as `K tan (alpha/2)`,

View SolutionThe value of horizontal component of earth's magnetic field at a place is `-.35xx10^(-4)T`. If the angle of dip is `60^(@)`, the value of vertical component of earth's magnetic field is about:
View SolutionA wire of mass 100kg is carrying a current of 2A towards increasing x in the form of `y=x^(2)(-2mlexle+2m)`. This wire is placed in a magnetic field `vecB=-0.02hatkT`. The acceleration of the wire:
View SolutionA long straight wire along the `z`- axis carries a current ` I` in the negative ` z- direction` . The magnetic vector field ` vec(B)` at a point having coordinates (x,y) in the ` Z = 0` plane is
View SolutionA dip needle vibrates in the vertical plane perpendicular to the magnetic meridian. The time period of vibration is found to be 2 sec. The same needle is then allowed to vibrate in the horizontal plane and the time period is again found to be 2 seconds. Then the angle of dip is
View SolutionA charged particle of mass `m` and charge `q` is accelerated through a potential differences of `V` volts. It enters of uniform magnetic field `B` which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View SolutionTwo magnet of equal mass are joined at right angles to each other as shown the magnet 1 has a magnetic moment 3 times that of magnet 2. This arrangment is pivoted so that it is free to rotate in the horizontal plane. In equilibrium what angle will the magnet 1 subtend with the magnetic meridian?

View SolutionThe magnetic moment of a short magnet is 8 `Am^(2)`. What is the magnetic induction at a point 20 cm away on its equatorial line form its mid point:
View SolutionA particle of charge `-16xx10^(-18) coulomb` moving with velocity `10 ms^(-1)` along the ` x- axis `, and an electric field of magnitude `(10^(4))//(m)` is along the negative ` z- ais`. If the charged particle continues moving along the ` x`- axis , the magnitude of `B` is
View SolutionThe moment of a short magnet is `4Am^(2)` the magnetic induction at a point on the axial. Line at a point 40 cm away from
View SolutionAn electron is projected with velocity `v_(0)` in a unifrom electric field E perpendicular to the field Again it is projectced with velocity `v_(0)` perpendicular to a unifrom magnetic field `B .` if `r_(1)` is initial radius of curvature just after entering in the electric field and `r_(2)` is initial radius of curvature just after entering in magnetic field then the ratio `r_(1)//r_(2)` is equal to .
View SolutionMagnetic field strength due to a short bar magnet on its axial line at a distance x is B. What is its value at the same distance on the equatorial line?
View SolutionIn Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
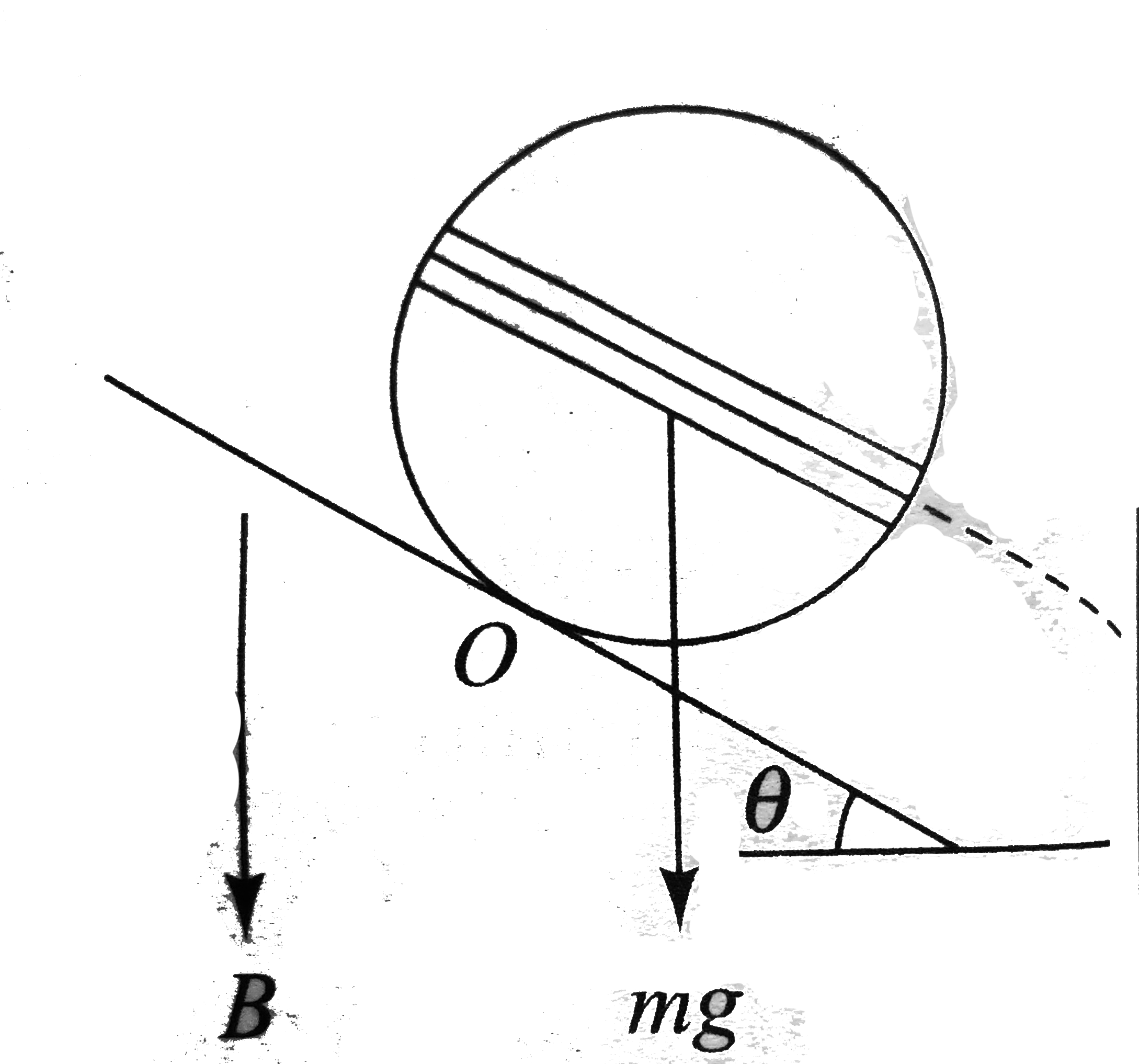
View SolutionIf a magnet is suspended at an angle `30^(@)` to the magnetic meridian and in this plane the dip needle makes an angle of `60^(@)` with the horizontal. The true value of dip is:
View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point `P` is
 .
.
View SolutionThe magnetic field due to a current carrying circular loop of radius `3 m` at as point on the axis at a distance of `4m` from the centre is `54 muT`. What will be its value at the centre of the loop/
View SolutionAn electron (mass `=9.1xx10^(-31)kg`, charge `=1.6xx10^(-19)C`) experiences no deflection if subjected to an electric field of `3.2x10^(5)V/m`, and a magnetic fields of `2.0xx10^(-3)Wb/m^(2)`. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
View SolutionAn electron accelerated through a potential difference V passes through a uniform transverse magnetic field and experiences a force F. If the accelerating potential is increased to 2V, the electron in the same field will experience a force
View SolutionA mass spectrometer is a device which selelct particle of equal mass. An ion with an electric charge `qgt0`. Starts at rest from s ource S and is accelerated through a potential difference V. it passes thorugh a hole into a region of constant magnetic field `vecB` perpendicular to the plane of the paper as shown in the figure-4.233. The particle is deflected by the magnetic field and emerges thorugh the bottom hole at a distance d from the top hole. The mass of the particle is:
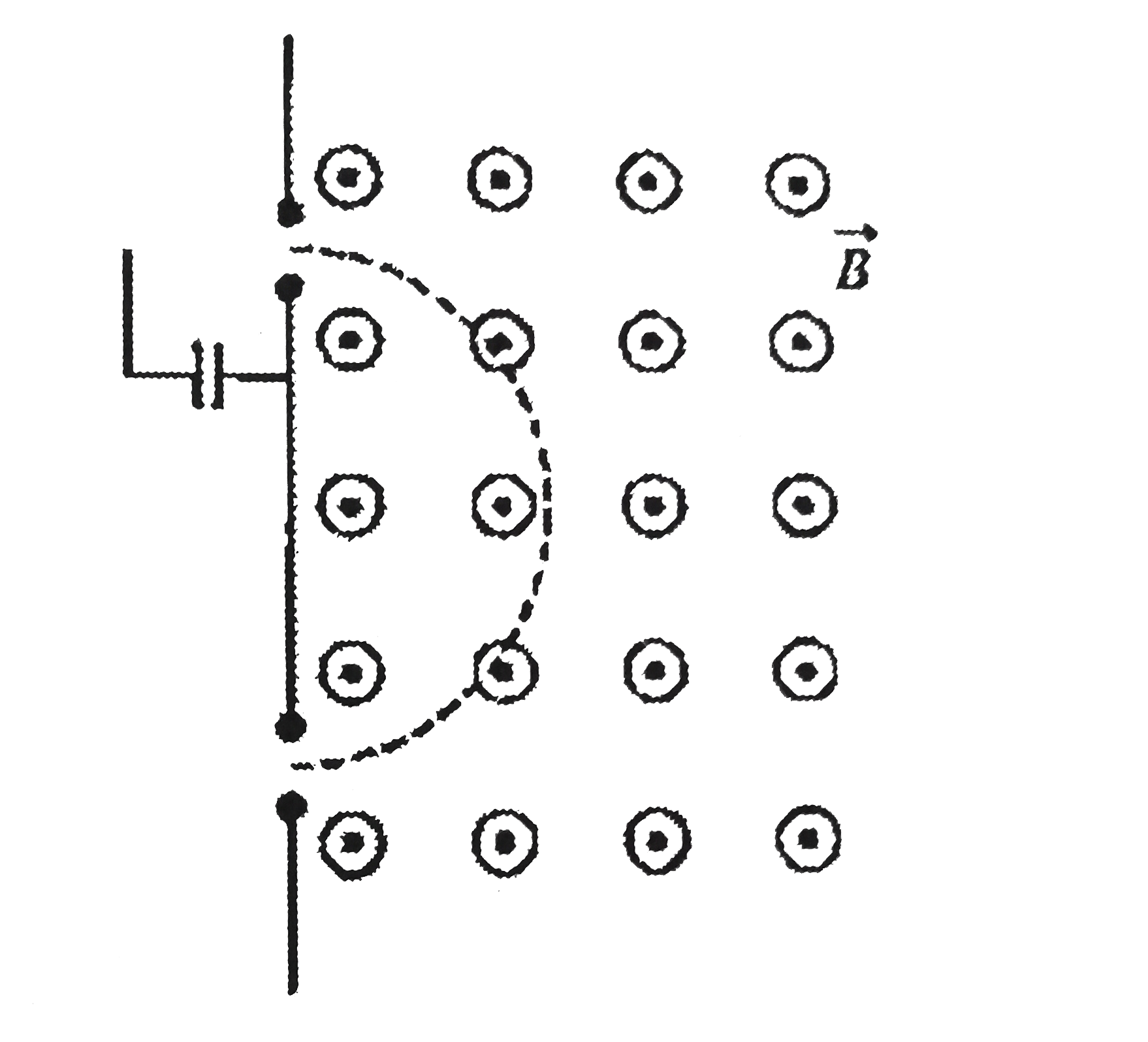
View SolutionThe field normal to the plane of a wire of `n` turns and radis `r` which carriers `i` is measured on the axis of the coil at a small distance `h` from the centre of the coil. This is smaller than the field at the centre by the fraction.
View SolutionA straight wire of diameter 0.5mm carrying a current 2A is replaced by another wire of diameter I mm carrying the saine current. The magnetic induction at a distance 2m away from the centre is :
View SolutionA block of mass m & charge q is released on a long smooth inclined plane magnetic field `B` is constant, unifrom, horizontal and parallel to surface a shown Find the time from start when block loses contact with the surface
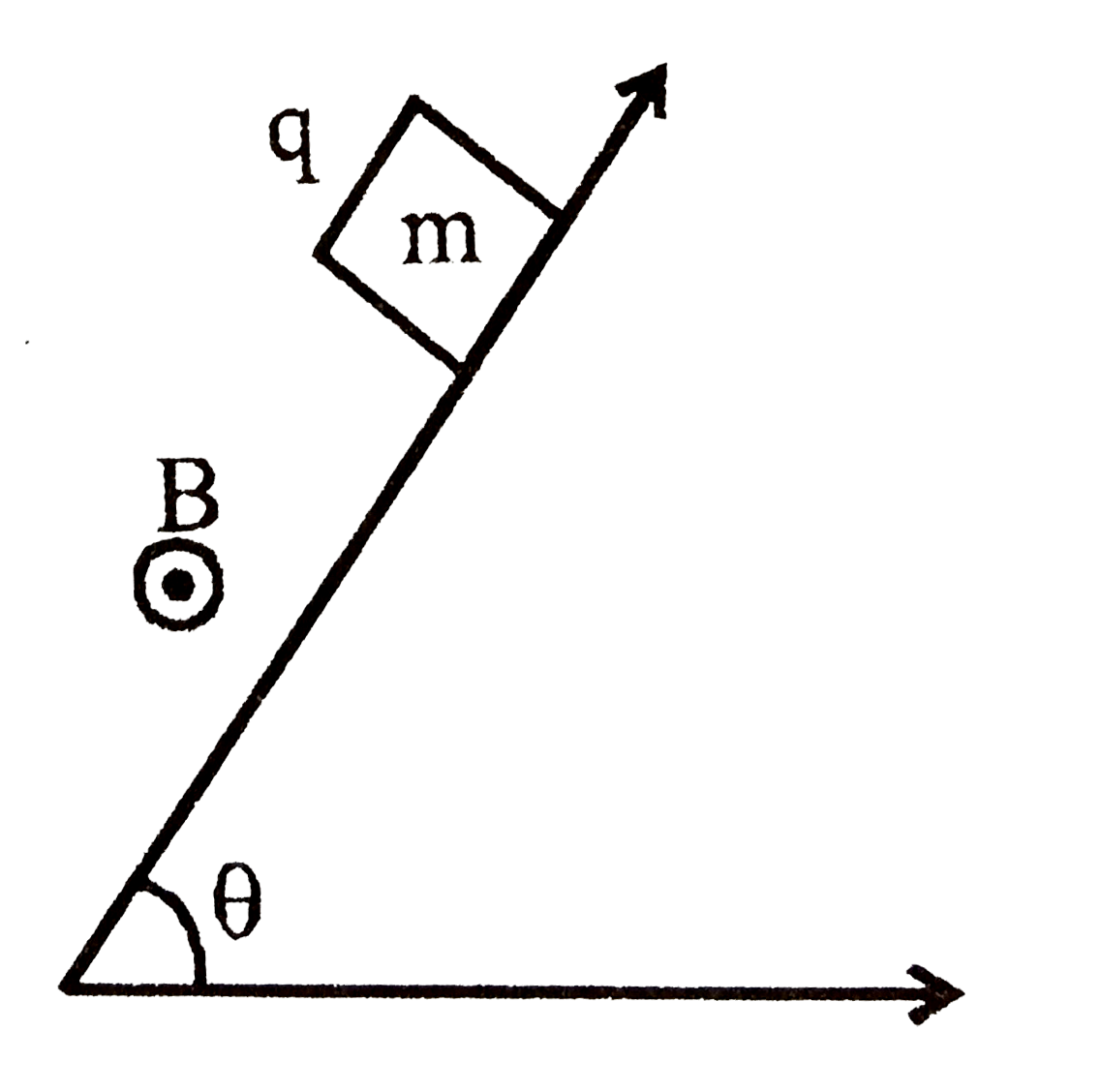 .
.
View SolutionA circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be `(1)/(8)` th to its value at the centre of the coil, is
View SolutionTwo infinite length wires carries currents `8A` and `6A` respectively and placed along `X` and `Y`-axis. Magnetic field at a point `P(0,0,d)m` will be
View SolutionAt t=0, a positively charged particle of mass m is projected from the origin with velocity `u_(0)` at an angle `37^(@)` fromn the x-axis as sown in the figure-4.235. a constant `vecB_(0)=B_(0)hatj` is present in space. After a time internal `t_(0)` velocity of particle may be:
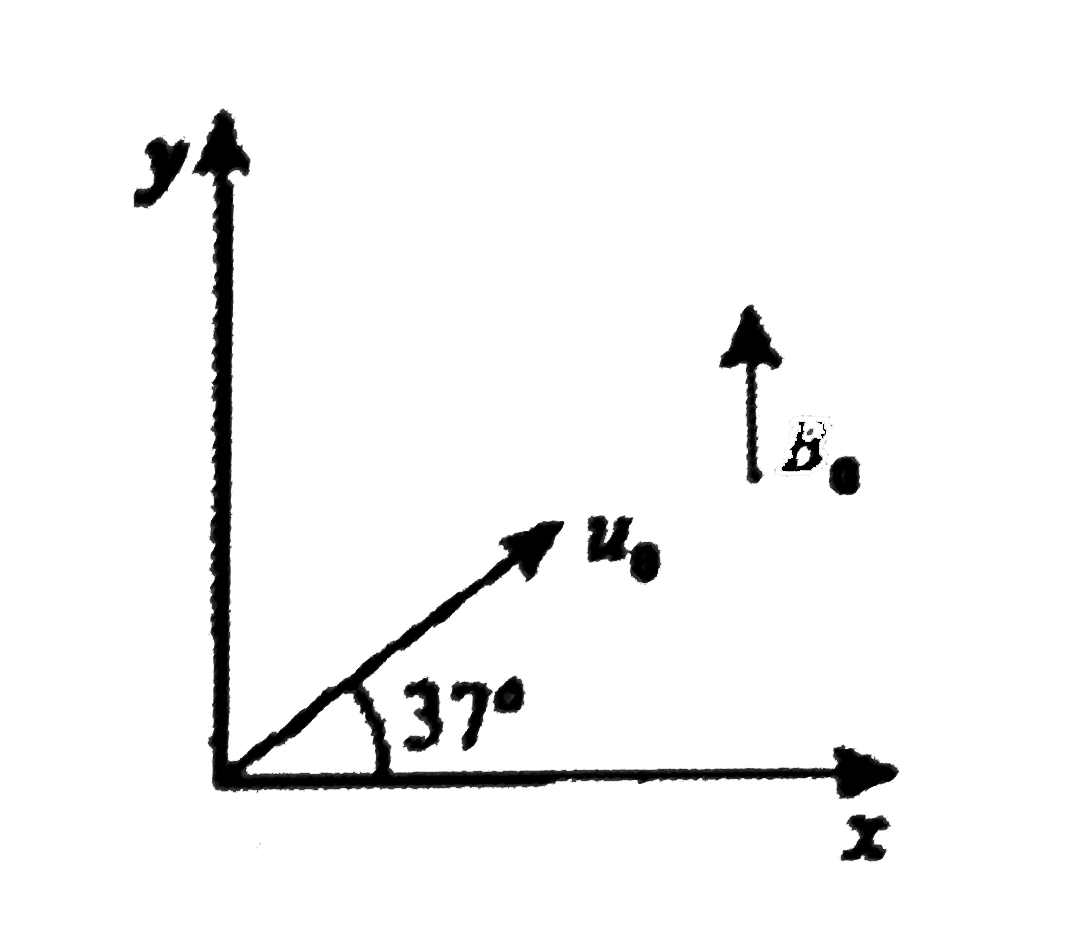
View Solution
Numerical MCQ questions and complete solutions for chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12