Complete Solutions to Practice Exercise of chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECTS OF CURRENT AND MAGNETISM |
| PHYSICS GALAXY | Practice Exercise |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
Find the magentic inducrtion at the centre of a recentagular wire frame whose diagonal is equal to `varphi = 30^(@)`, the current flowing in the frame equlas `I = 5.0 A`.
View SolutionFind the magentic induction of the field at the pont `O` if a current-carrying wire has the shape shown in Figa,b,c The raidius of the curved part of the of the weir is `R` the linear parts are assumed to be very long.
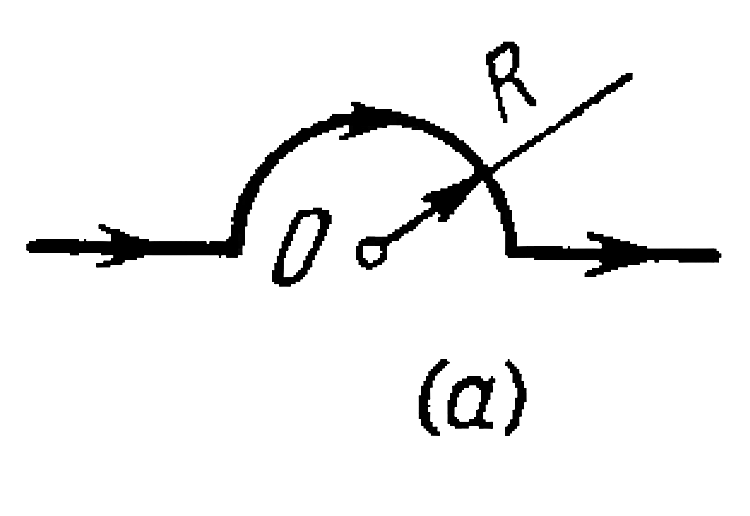
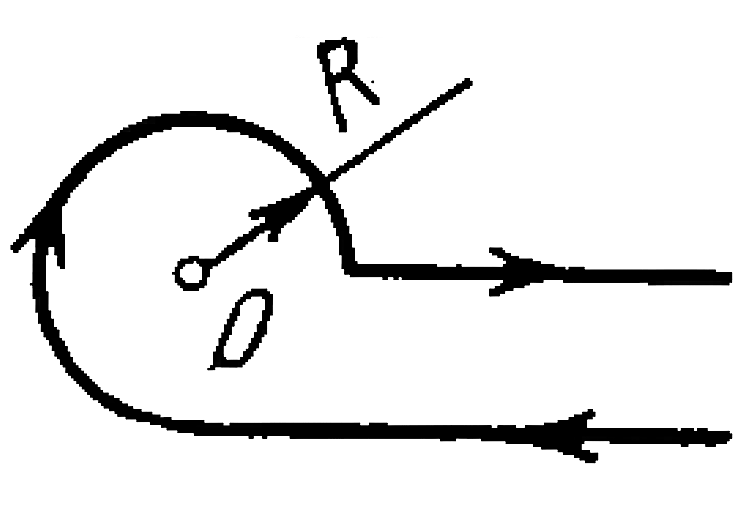

View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
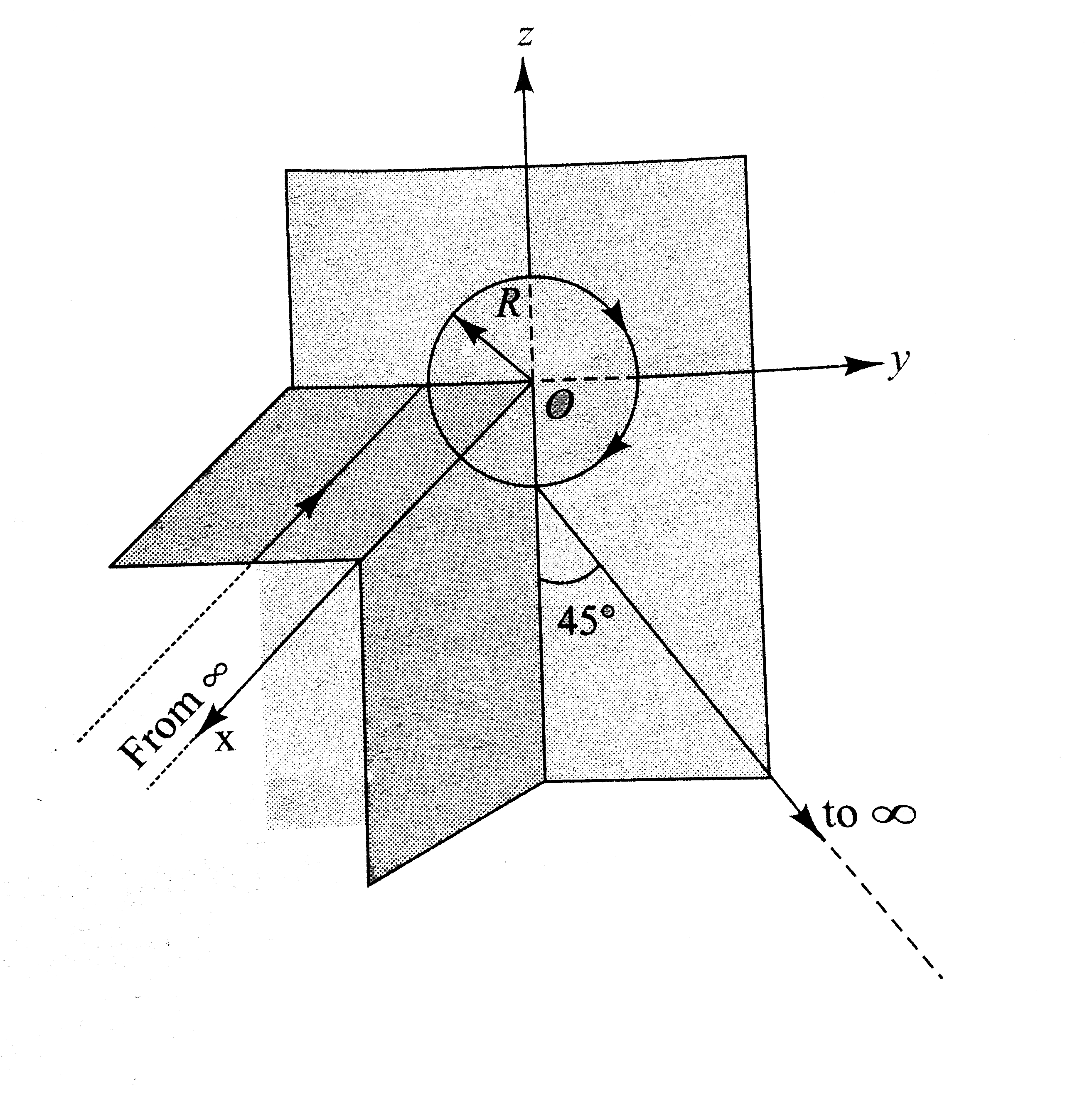
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View SolutionIn the figure-4.30 shown two circular arcs are joined to make a closed loop carrying current `l`. Frnd the magnetic induction at the common centre 0.

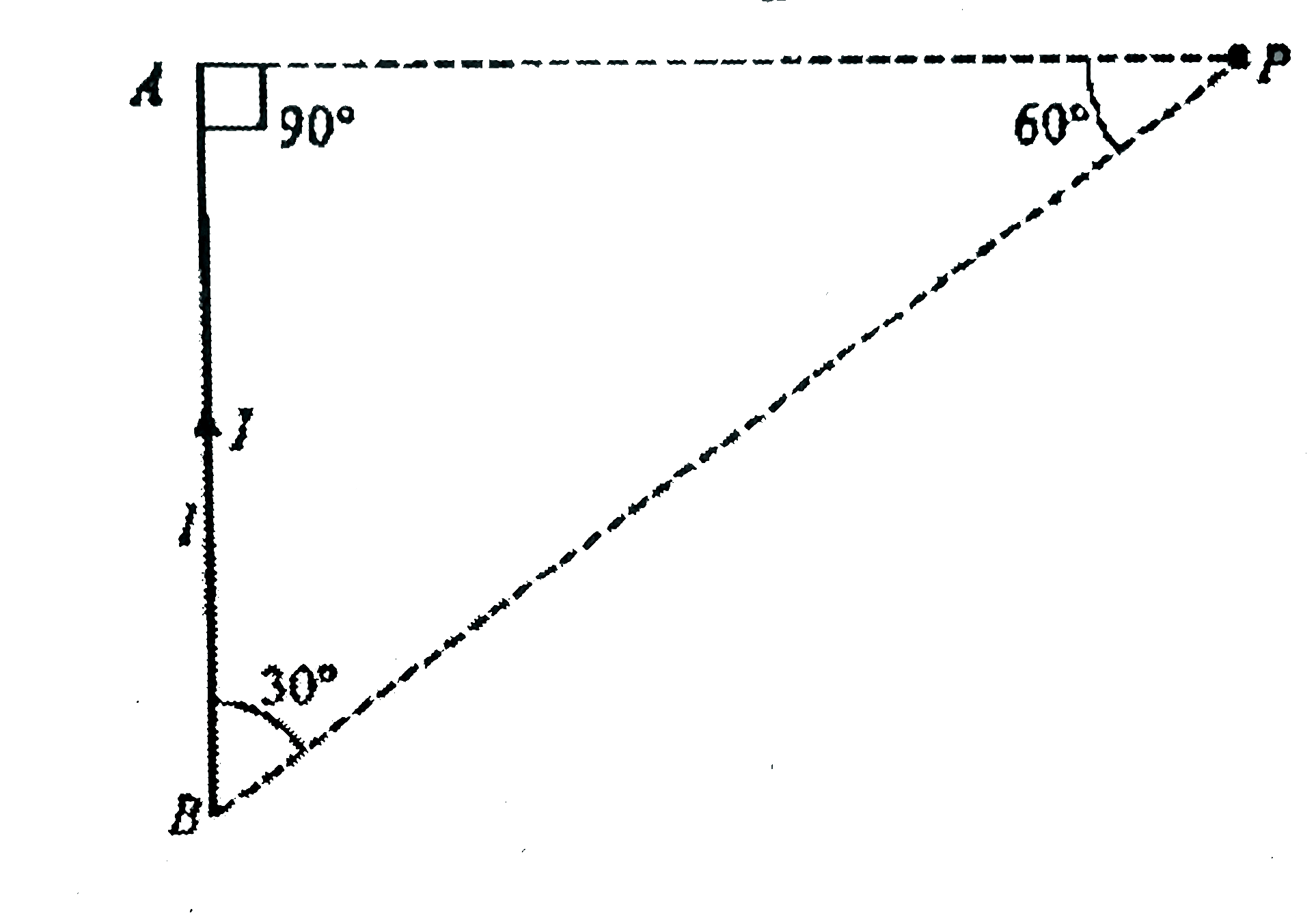
View SolutionFind the magnetic induction at point P due to a current carrying wire AB as shown in figure-4.31
View SolutionFind magnetic induction at point O in the figure-4.32 shown due to the current carrying loop with current/ as shown .

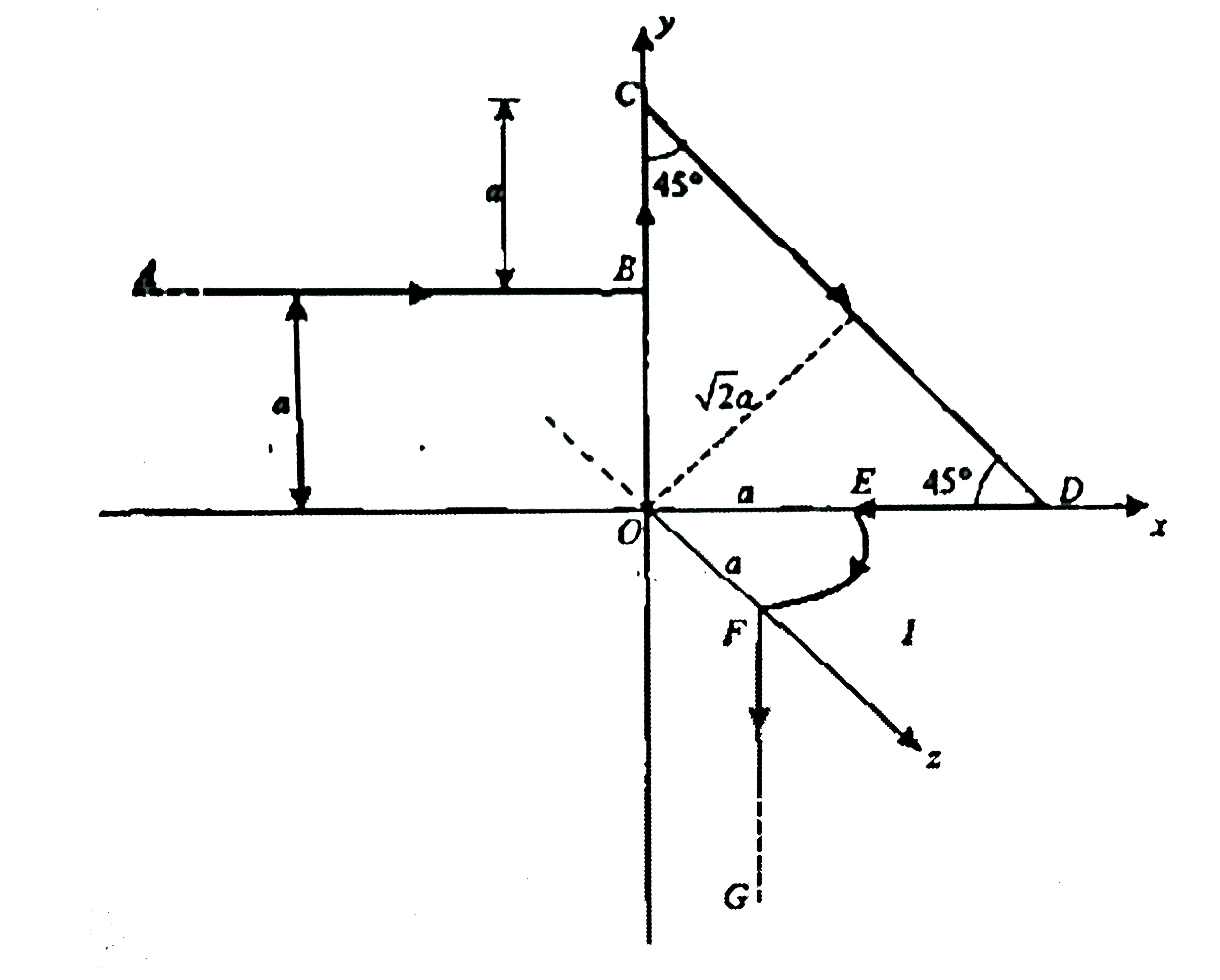
View SolutionFind the magnetic induction vector at origin O due to the current carrying wire configuration as shown in figure-4.33.
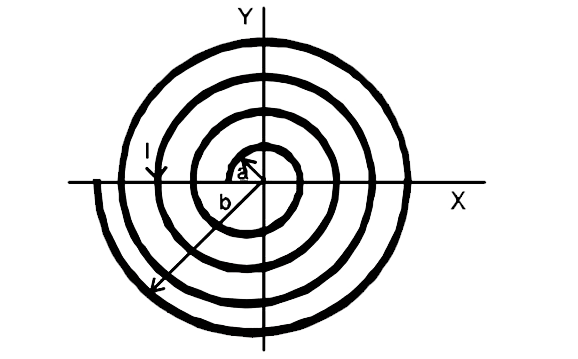
View SolutionA long insulated copper wire is closely wouind as a spiral of 'N' turns . Thw spiral has inner radius 'a' and outer radius 'b' . The spiral lies in the ` XY `plane and a steady current ' I' flows through the wire . The Z - component of the magnetic field at the centre of the spiral is
View SolutionFigure shows a long and thin strip of width b which carries a current `I`. Find magnetic induction due to the current in strip at point P located at a distance `r` from the strip in the plane of strip as shown in figure-4.35.

View SolutionTwo long parallel wires carrying current ` 2.5 amperes` and `I ampere` in the same direction ( directed into the plane of the paper) are held at `P and Q` respectively such that they are perpendicular to the plane of paper. The points `P and Q` are located at a distance of ` 5 metres and 2 metres` respectively from a collinear point `R` ( see figure)
(i) An electron moving with a velocity of ` 4xx10^(5) m//s ` along the positive ` x- direction ` experiences a force of magnitude `3.2xx10^(-20) N` at the point `R`. Find the value of `I`.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude `2.5 amperes` may be placed so that the magnetic induction at `R` is zero.
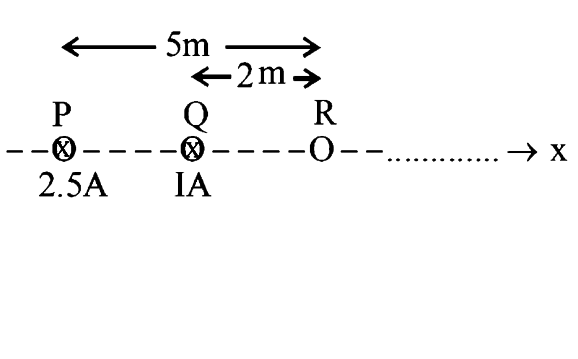
View SolutionA tightly- wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surgace current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
View SolutionA coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) `r gt a`, (b) `a lt r lt b` and (c) `b gt r gt c`

View SolutionA thin conducting strip of width his tightly wound in the shape of a very long cylindrical coil with cross-sectional radius R to make a single layer straight solenoid as shown in figure-4.81. A direct current `I` flows through the strip. Find the magnetic induction inside and outside the solenoid as a function of the distance r from its axis.

View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionA capacitor of capacitance C is connected to a battery of EMF E for a long time and then disconnected. The charged capacitor is then connected across a long solenoid having n turns per meter in its closely packed winding on its core. After connections it is found that the voltage across the capacitor drops to `E//eta` in a time `Delta t`. In this period estimate the average magnetic induction at the centre of solenoid.
View SolutionA current `I ` flows radius along a lengthy thin-walled tube of radisu `R` with longiitual slit of width `h`. Find the induction of the magnietic field inside the tube under the condition `h lt lt R`
View SolutionA direct current `I` flows along a lengthly straight wire. From the point `O` (fig) the current sperads radially all over an infinite conducting plane paerpendicular to the wire. Find the magnitude induction at all points of space.
View SolutionA toroid of total 1000 turns is made by using a tore of average radius 25cm. What is the magnetic induction inside the tore if a current of2A is passed through it and the relative magnetic permeability of the tore material is `mu = 100`
View SolutionA beam of charged particle, having kinetic energy `10^3 eV`, contains masses `8xx10^(-27) kg and 1.6xx10^(-26) kg` emerge from the end of an accelerator tube. There is a plate at distance `10^2 m` from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionAn electron moving with a velocity `10^(8) m//s` enters a magnetic field at an angle of `20^(@)` to the direction of the field. Calculate
(a) The value of magnetic induction so that the helical path radius will be 2m.
(b) The time required to execute one revolution of the helical path.
(c) The pitch o fhelical path followed by the electron.
View SolutionA stream of protons and deuterons in a vacuum chamber enters a uniform magnetic field. Both protons and deuterons have been subjected to same accelerating potential, hence the kinetic energies of the particles are the same. If the ion-stream is perpendicular to the magnetic field and the protons move in a circular path of radius 15 cm, find the radius of the path traversed by the deuterons. Given that mass of deuteron is twice that of a proton.
View SolutionAn electron gun `G` emits electons of energy `2 keV` travelling in the positive x-direction. The electons are required to hit the spot `S` where `GS=0.1 m`, and the line `GS` makes an angle of `60^@` with the x-axis as shown in figure. A uniform magnetic field `B` parallel to `GS` exists in the region outside the electron gun.
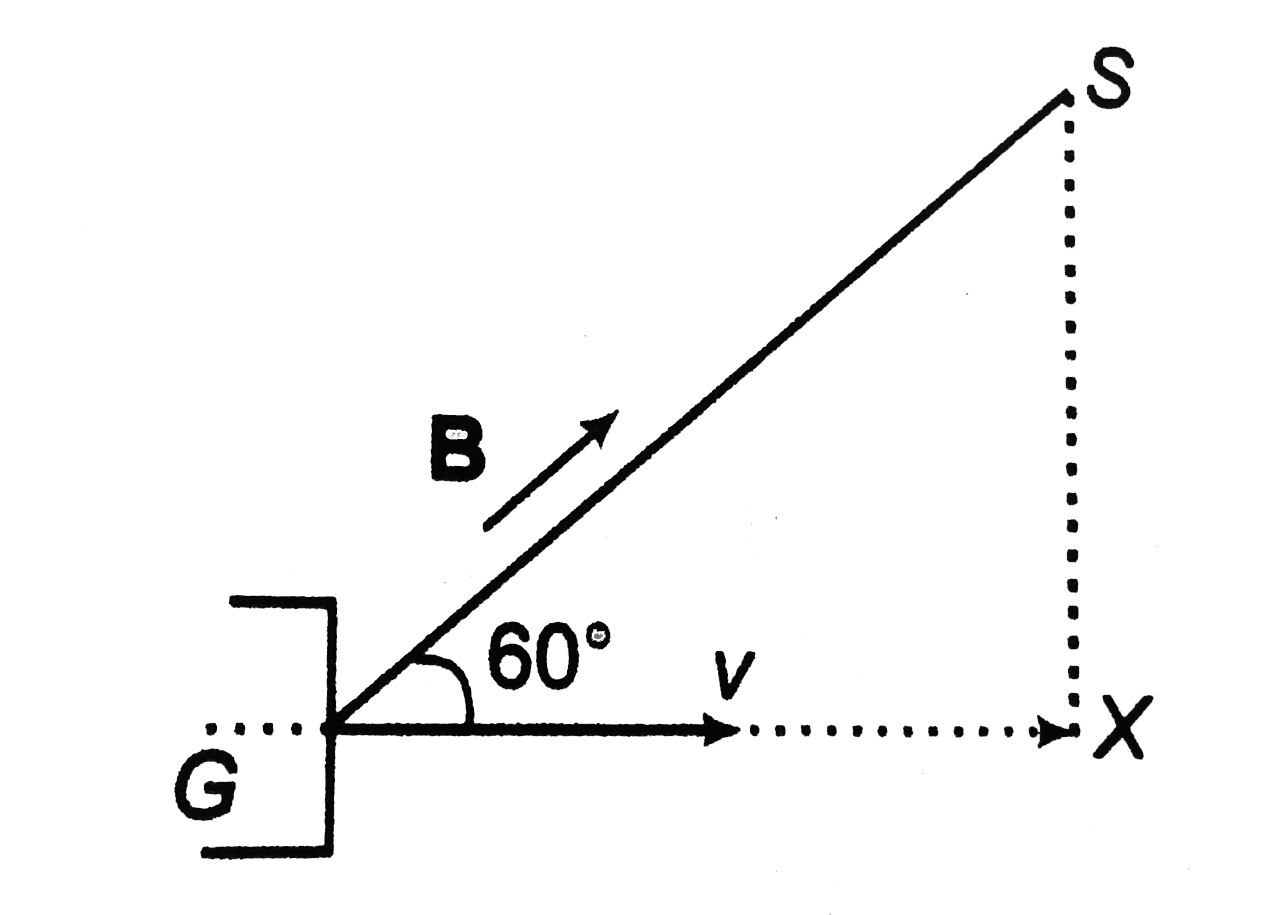
find the minimum value of `B` needed to make the electrons hit `S`.
View SolutionA `15000 V` electron is describing a circle in a uniform field of magnetic indnction 250G acting at right angle to it. Calculate tbe radius oftbe circle.
View SolutionA slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction `B_1 and B_2.` Find the specific charge `q//m` of the particles.
View SolutionA direct current flowing through tbe winding of a long cylindrical solenoid ofradius R produces a uniform magnetic induction B in it. An electron travelling at velocity v enters into tbe solenoid along the radial direction between its turn at right angles to the solenoid axis. After a certain time tbe electron deflected by magnetic field leaves the solenoid. Calculate the time which the electron spends inside the solenoid.
View SolutionTwo long parallel wires carrying current ` 2.5 amperes` and `I ampere` in the same direction ( directed into the plane of the paper) are held at `P and Q` respectively such that they are perpendicular to the plane of paper. The points `P and Q` are located at a distance of ` 5 metres and 2 metres` respectively from a collinear point `R` ( see figure)
(i) An electron moving with a velocity of ` 4xx10^(5) m//s ` along the positive ` x- direction ` experiences a force of magnitude `3.2xx10^(-20) N` at the point `R`. Find the value of `I`.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude `2.5 amperes` may be placed so that the magnetic induction at `R` is zero.
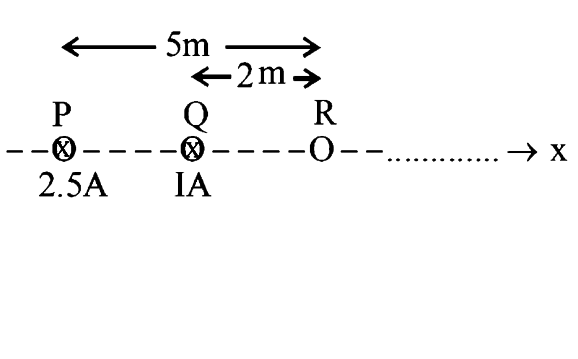
View SolutionIn a right handed coordinate system XY plane is horizontal and Z-axis is vertically npward. A uniform magnetic field exist in space in vertically npward direction with magnetic induction B. A particle with mass m and charge q is projected from the origin of the coordinate system at `t= 0` with a velocity vector given as
`vec(v) = v_(1) hat(i) + v_(2) hat(k)`
Find the velocity vector of the particle after time t.
View SolutionInside a cylindrical capacitor of inner radius a and outer radius b, an electron is projected from the surface of inner cylindrical shell perpendicular to it with an initial velocity. In the annular region between the two cylindrical shells a uniform magnetic induction B exist in direction parallel to the axis of capacitor. Find tbe maximum initial velocity with which tbe electron is to be projected so that it will not hit the outer shell.
View SolutionFigure shows a wire AB of mass m placed on a rough inclined plane of inclination `alpha` and static friction coefficient `mu`. The wire carries a current I. Find the minimum magnitude of magnetic induction required to slide the wire up the inclined plane if direction of magnetic induction is normal to plane as shown in figure.

View SolutionA wire of 60 cm length and mass 16 gm is suspended by a pair of flexible leads in a magnetic field of induction 0.40 T. What are the magnitude and direction of the current required to remove the tension in the supporting leads?

View SolutionTwo long parallel wires carry currents of equal magnitude but in opposite directions. These wires are suspended from rod PQ by four chords of same length L as shown in Fig The mass per unit length of the wires is `lambda`. Determine the value of `theta` assuming it to be small.

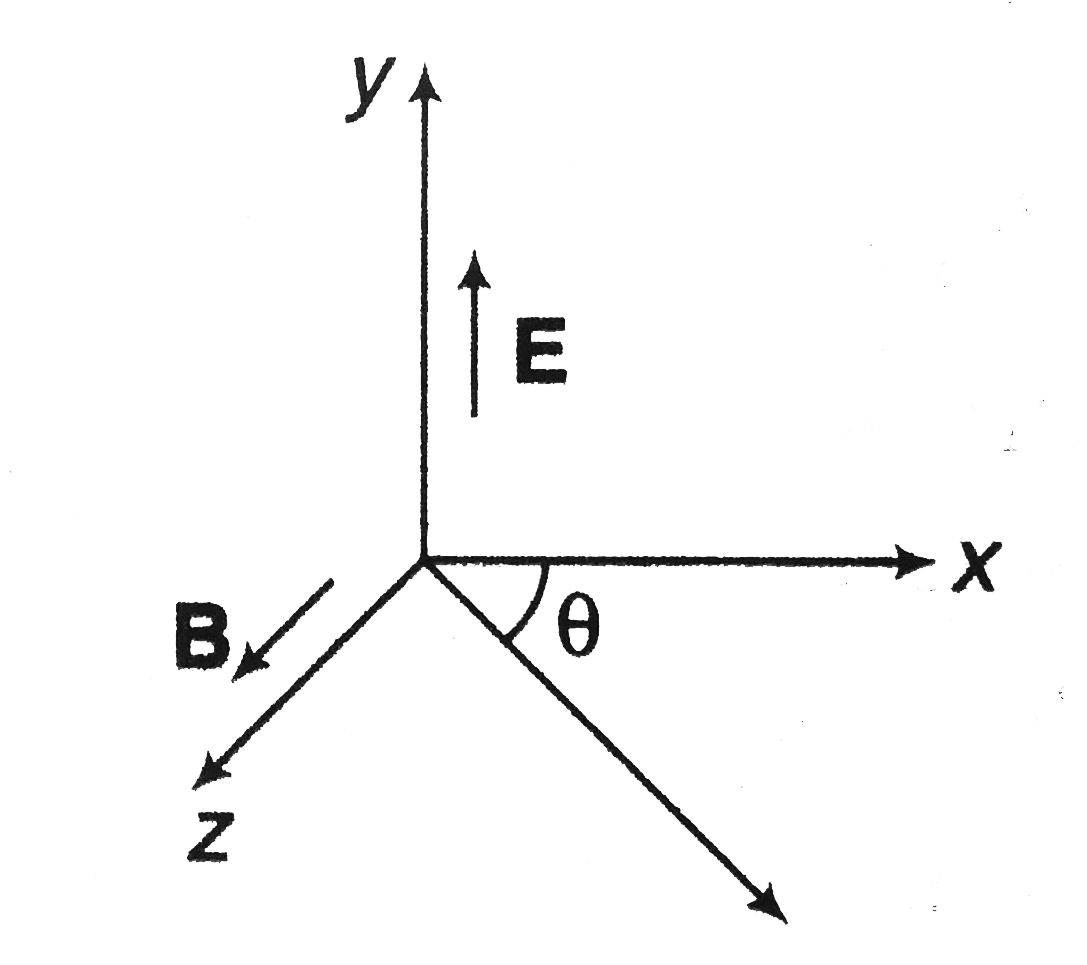
View SolutionProtons move rectilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields `E` and `B`. The trajectory of protons lies in the plane xz as shown in the figure and forms an angle 9 with x-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
View SolutionA loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

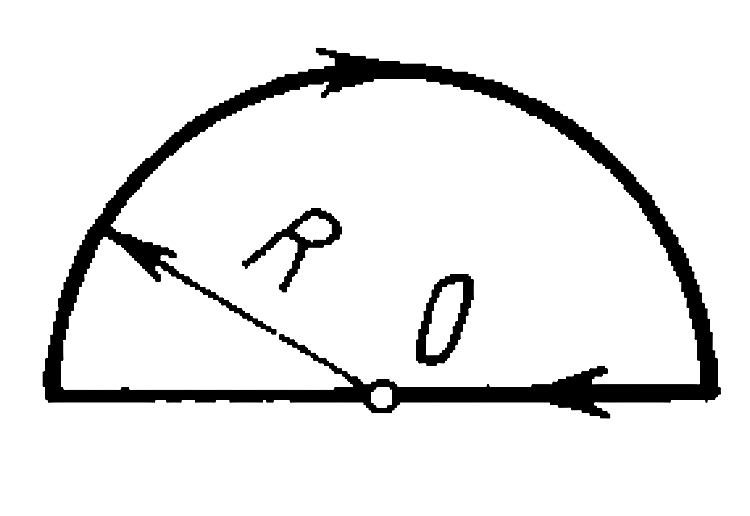
View SolutionFind the magtiude and direction of a force vector acting on a unit length of a thin wire, carrying a current `I = 8.0 A`, at a point `O`. If the wire is hent as shown in (a) Fig with curvature radius `R = 10 cm`
(b ) Fig the distance between the long parallel segments of the wire being equal to `l = 20 cm`.

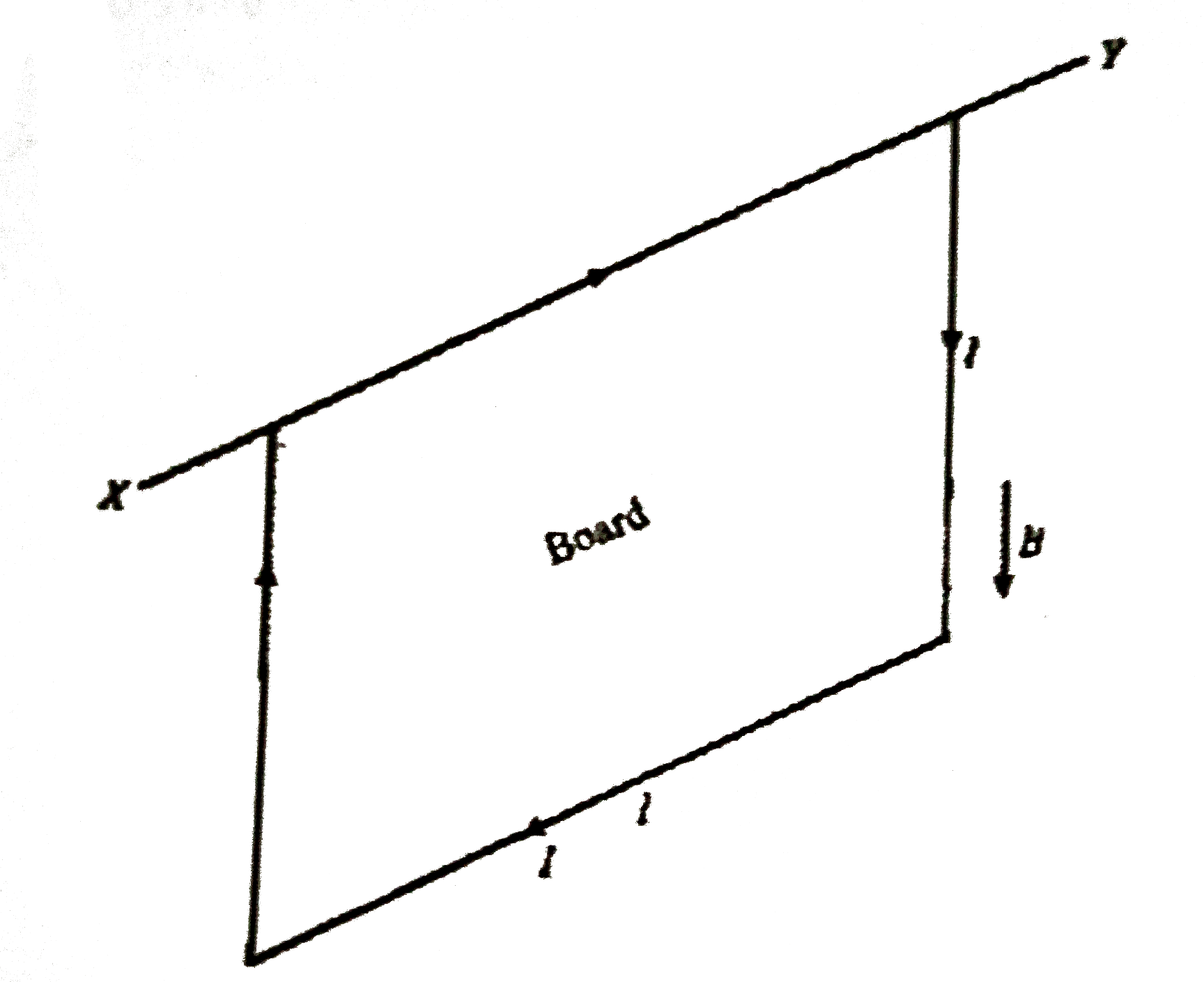
View SolutionA square cardboard of side I and mass m is suspended from a horizontal axis XY as shown in figure. A single wire is wound along the periphery of board and carrying a clockwise current I. At t = 0, a vertical downward magnetic field of induction B is switched on. Find the minimum magnitude of B so that the board will be able to rotate up to horizontal level.
View SolutionFigure shows a horizontal wire MN of length I and mass mis placed in a magnetic field B. The ends of wire are bent and dipped in two bowls containing Hg which are connected to an external circuit as shown. If key is pressed for a short time `delta t`.due to which a charge q suddenly flows in the circuit. Find the maximum height above initial level the wire MN, it will jump.
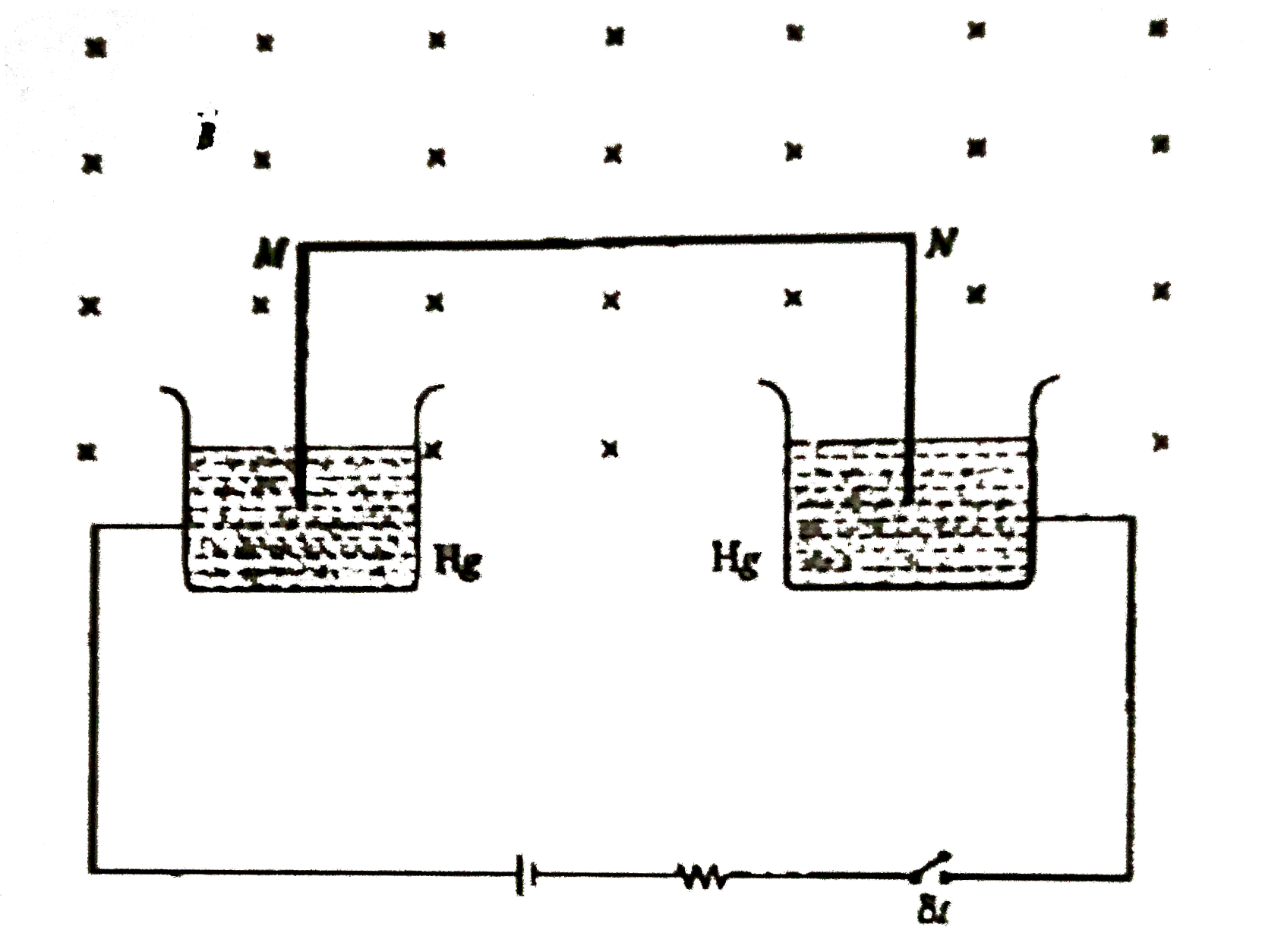
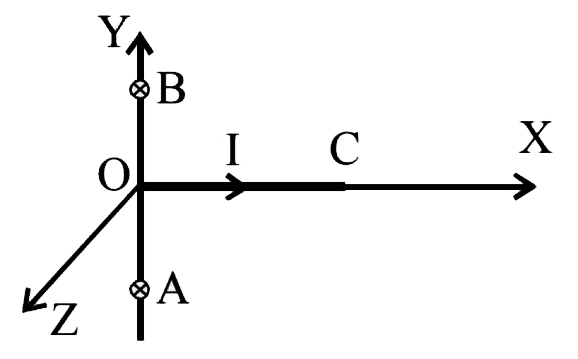
View SolutionA straight segment `OC`(of length L meter) of a circuit carrying a current `I amp` is placed along the ` x- axis` ( fig.). Two infinetely long straight wires ` A and B` , each extending from ` z = -oo to +oo`, are fixed at ` y = -ameter and y = +a meter` respectively, as shown in the figure.
If the wires ` A and B` each carry a current `I amp` into the plane of the paper, obtain the expression for the force acting on the segment ` OC`. What will be the force on `OC` if the current in the wire `B` is reversed?
View SolutionA positively charged particle having charge `q_1 = 1 C` and mass `m_1 =40 gm` is revolving along a circle of radius `R=40 cm` with velocity `v_1 = 5 ms^-1` in a uniform magnetic field with center of circle at origin `O` of a three-dimensional system. At `t=0`, the particle was at (0, 0.4m, 0) and velocity was directed along positive x direction. Another particle having charge `q_2 = 1 C` and mass `m_2 = 10g` moving uniformly parallel to positive z-direction with velocity `v_2 = 40//pi ms^-1` collides with revolving particle at `t=0` and gets stuck to it. Neglecting gravitational force and coulomb force, calculate x-, y- and z-coordinates of the combined particle at `t= pi//40 s`.
View SolutionFrom the surface of a round wire of radius a carrying a direct current i, a positive charge q escapes with a velocity `v_0` perpendicular to the surface. Find what the maximum distance of the electron will be from the axis of the wire before it turns back due to the action of the magnetic field generated by the current.
View SolutionIn the Bohr model of the hydrogen atom, the electron circuulates around the nucleus in a path of radius `5xx10^-11m` at a frequency of `6.8xx10^15Hz`.
a. What value of magnetic field is set up at the centre of the orbit?
b. What is the equivalent magnetic dipole moment?
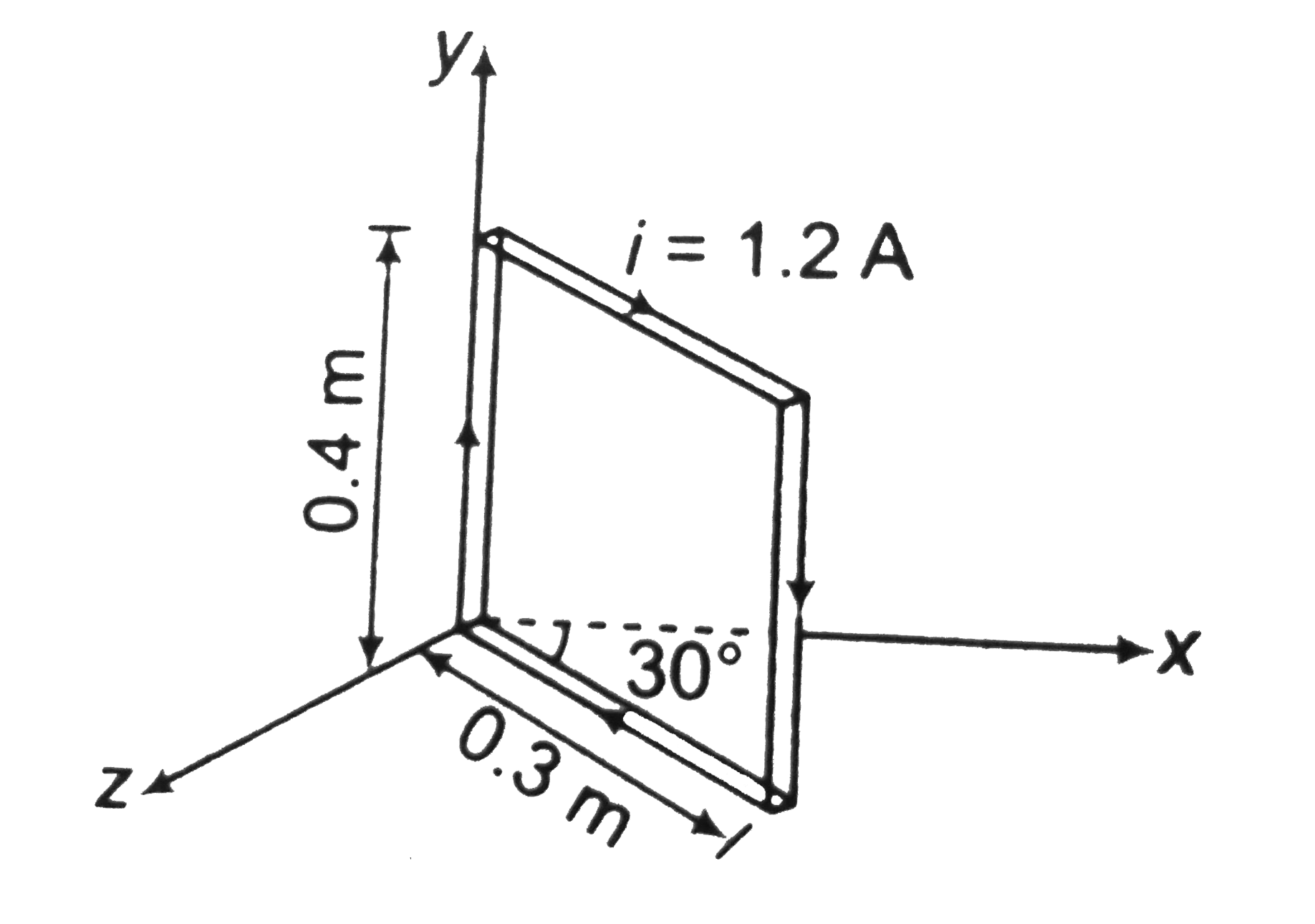
View SolutionA rectangular loop consists of `N = 100` closed wrapped turns and has dimensions `(0.4 m xx 0.3 m)`. The loop is hinged along the y-axis and its plane makes an angle `theta = 30^@` with the x-axis. What is the magnitude of the torque exerted on the loop by a uniform magnetic field `B = 0.8 T` directed along the x-axis when current is `i = 1.2 A` in the direction shown. What is the expected direction of rotation of the loop?
View SolutionA coil in the shape of an equilateral triangle of side 0.02 m is suspended from a vertex such that it is hanging in a vertical plane between the pole pieces of a permanent magnet producing a horizontal magnetic field of `5 xx 10^(-2) T.` Find the couple acting on the coil when a current of 0.1 A is passed through it and the magnetic field is parallel to its plane.
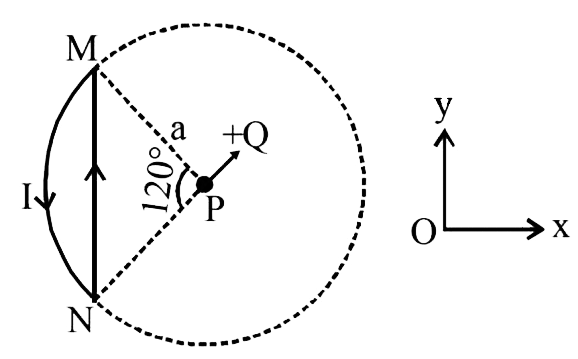
View SolutionA wire loop carrying `I` is placed in the ` x-y`plane as shown in fig.
(a) If a particle with charge ` +Q` and mass `m` is placed at the centre `P` and given a velocity ` vec(v)` along `NP`(see figure), find its instantaneous acceleration.
( b) If an external uniform magnetic induction field ` vec(B) = Bhat(i)` is applied , find the force and the torque acting on the loop due to this field.
View SolutionA coil of radius R carries current `i_1`. Another concentric coil of radius `r(rlt ltR)` carries current `i_2`. Planes of two coils are mutually perpendicular and both the coil are free to rotate about common diametre. Find maximum kinetic energy of smaller coil when both the coils are released, masses of coils are M and m, respectively.
View SolutionA small coil `C` with N = 200 turns is mounted on one end of a balance beam and introduced between the poles of an electromagnet as shown in Fig. The cross sectinal area of the coil is `S = 1.0 cm^(2)`, the length of the arm `OA` of the balance beam is `l = 30 cm`. When there is no current in the coil the balance is irl equilibrium. On passing a current `I = 22 mA` through the coil the equiibrium is restroed by putting the additional counterweight of mass `Delta m = 60 mg` ont he balnace pan. Find the magnetic induction at the spot where the coil is located.
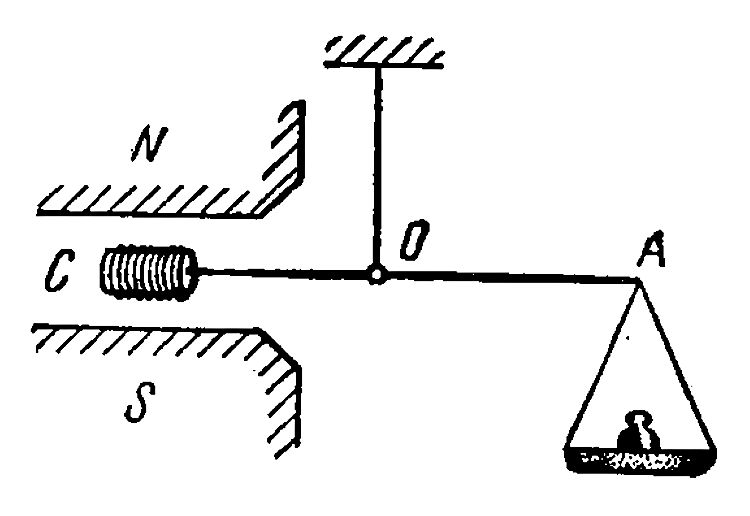
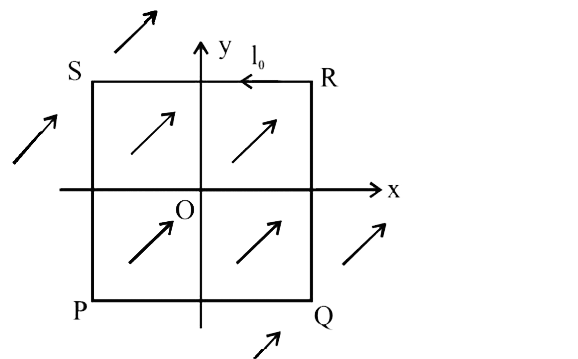
View SolutionA uniform constant magnetic field `B` is directed at an angle of `45^(@)` to the `x axis` in the ` xy`- plane . ` PQRS` is a rigid, square wire frame carrying a steady current `I_(0)`, with its centre at the origin `O`. At time ` t = 0`, the frame is at rest in the position as shown in figure , with its sides parallel to the ` x and y` axis. Each side of the frame is of mass `M` and length `L`.
(a) What is the torque `tau` about `O` acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Deltat`, and the axis about this rotation occurs .`( Deltat is so short that any variation in the torque during this interval may be neglected .) Given : the moment of interia of the frame about an axis through its centre perpendicular to its about an axis through its centre perpendicular to its plane is `(4)/(3) ML^(2)`.
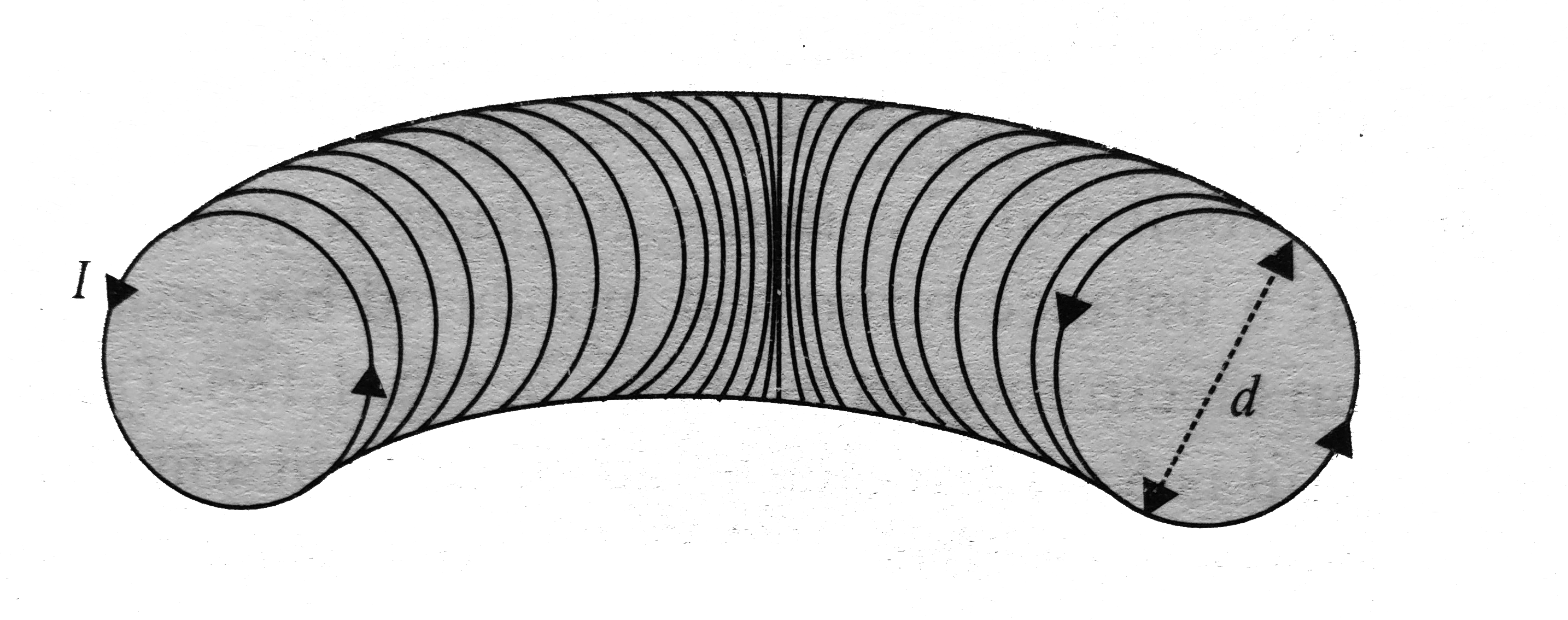
View SolutionCalculating the magnetic moment ( in `Am^2`) of a thin wire with a current I=8A, wound tightlly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.
View SolutionA flat circular coil with 10 turns of wire on it has a diameter 20mm and carries a current 0.5A. It is mounted inside a long solenoid that has 200 turns and the length of the solenoid is 0.25m. The current passing through the solenoid is 2.4A. Calculate the torque needed to hold the coil with its axis perpendicular to that of solenoid.
View SolutionA coil al a moving Coil galvanometer twists through `90^@` when a current of one microampere is passed through it. If the area of the coil is `10^-4 m^2` and it has `100` turns, calculate the magnetic field of the magnet of the galvanometer. Given, `k = 10^-8N -m /degree.`
View SolutionA short bar magnet is placed in magnetic meridian with its north pole pointing toward south: Its magnetic moment is `2Am^(2)`. Neutral point is obtained 10cm from centre of magnet toward north. Calculate horizontal component of earth's magnetic field.
View SolutionA magnetic dipole of magnetic moment `6Am^(2)` is lying in a horizontal plane with its north pole pointing toward `60^(@)` East of North. Find the net horizontal magnetic field at a point· on the axis of the magnet 0.2m away from it. Horizontal Component of earth field at this place is `30 mu T`.
View SolutionA coil of 50 turns and 10cm diameter is made out of a wire of resistivity `2 xx 10^(-6) Omega cm` and cross sectional radius 0.1mm. The coil is connected to a source of EMF `10 V` and of negligible internal resistance.
(a) Find the current through the coil
(b) What must be potential difference across the coil so as to nullify the horizontal component of earth's magnetic field, `0.314 xx 10^(-4) T` at the centre of the coil. How should the coil be placed to achieve. this result?
View SolutionTwo circular coils `C_1` and `C_2` each of 100 turns are held in such a way that `C_1` lies in vertical plane and the other `C_2` in the horizontal plane, with their centres coinciding. The radii of the coils are `r_1=20cm` and `r_2=30cm`. The directions of currents `I_1` and `I_2` passed through the two coils are such that earth's magnetic field at the common centre is neutralised completely. If `H=27*8Am^-1` and angle of dip is `30^@`. Calculate the values of `I_1` and `I_2`.
View SolutionA magnetic needle suspended in a vertical plane at `30^@` from the magnetic meridian makes an angle of `45^@` with the horizontal. Find the true angle of dip.
View SolutionTwo small magnets of magnetic moments `0.108Am^(2)` and `0.192 Am^(2)` are placed at some separation that their axes are mutually perpendicular. If the distance of the point of intersection of axes of magnets be respectively 30 cm and 40 cm from these magnets, then find the resultant magnetic induction at the point of intersection. The magnetic moments of both the magnets are pointing toward the point of intersection of their axes.
View SolutionA short magnet porduces a deflection of `30^(@)` when placed at certain distance in tanA position of magnetometer. If another short magnet of double the length and thrice the pole strength is placed at the same distance in tan B position of the magnetometer, the deflection produced will be-
View SolutionA magnetic needle performs `20` oscillations per minute in a horizontal plane. If the angle of dip be `30^@`, then how many oscillation per minute will this needle perform in vertical, north south plane and in vertical east -west plane?
View Solution
Practice Exercise questions and complete solutions for chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12