Complete Solutions to U.N.P of chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECTS OF CURRENT AND MAGNETISM |
| PHYSICS GALAXY | U.N.P |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
An `alpha-`particle is accelerated by a potential difference of `10^4 V.` Find the change in its direction of motion, if it enters normally in a region of thickness 0.1 m having transverse magnetic induction of 0.1 tesla. (Given: mass of `alpha-`particle `6.4xx10^(-27)`kg).
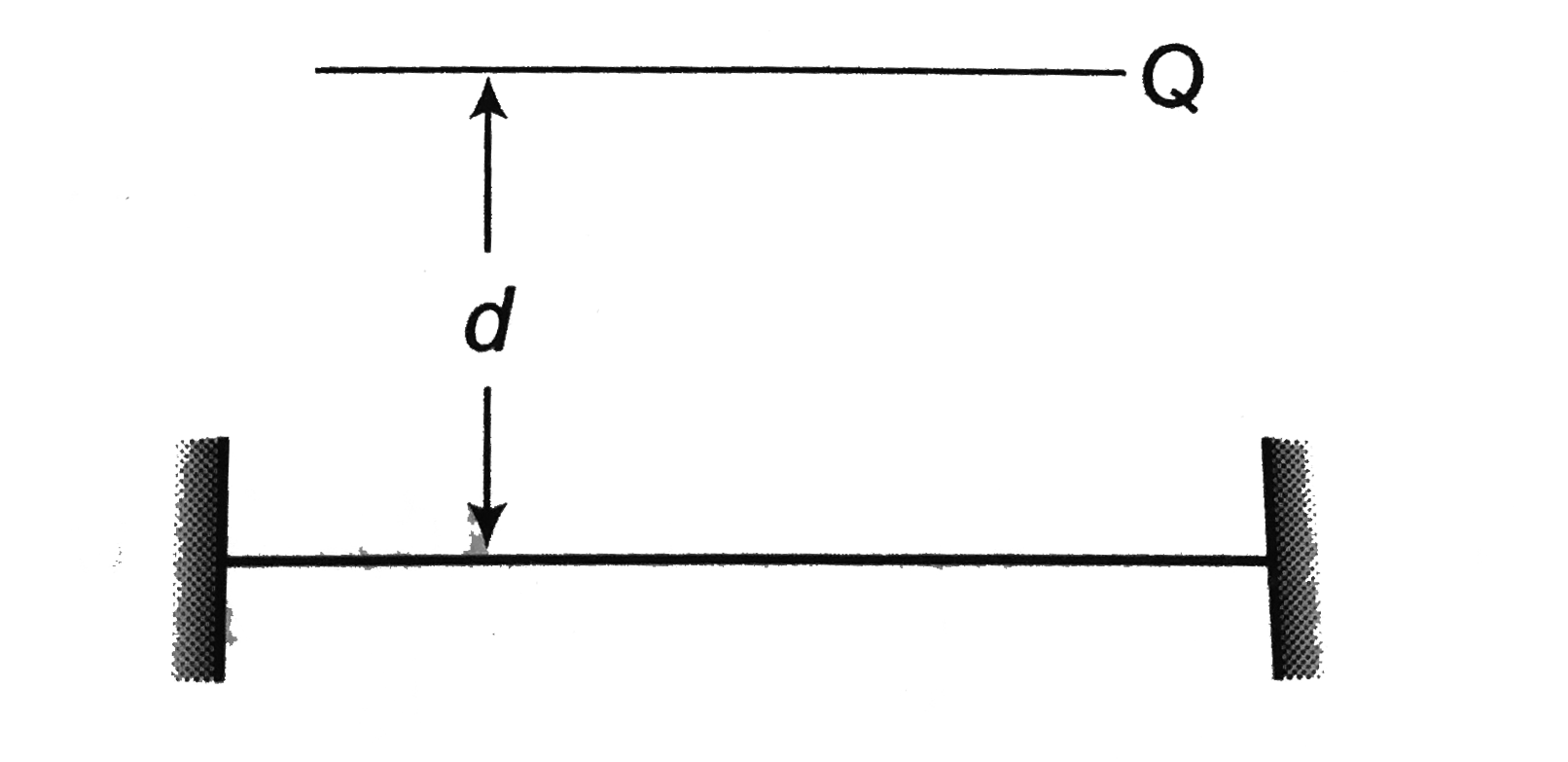
View SolutionA long horizontal wire `AB`, which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another parallel long wire `CD` which is fixed in a horizontal plane and carries a steady current of ` 30 A`, as shown in figure. Shown that when `AB` is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.

View SolutionA beam of charged particle, having kinetic energy `10^3 eV`, contains masses `8xx10^(-27) kg and 1.6xx10^(-26) kg` emerge from the end of an accelerator tube. There is a plate at distance `10^2 m` from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionA long straight cylindrical hollow pipe has inner and outer radii 1 cm and 2 cm respectively. It carries a current 100 A. Calculate the magnetic field at distance (a) 0.5 cm, (b) 1.5 cm and (c) 4 cm from the axis of pipe.
View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction `B` is applied at right angle to the strip.
(a) Calculate the drift velocity `v_d` of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field `E` Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field `E_H` across the conductor until the forces of this electrostatic field `E_H` balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field `E_H`?
Assume that n, the number of conductor electrons per unit volume is `1.1xx10^(29) m^-3, h = 0.02 m, w= 0.1 cm, i = 50 A, and B=2 T.`

View SolutionA 2 keV positron is projected into uniform field of induction B of `0.10 T` with its velocity vector making an angle of `89^(@)` with B. Convince your-self that the path will be a helix, its axis being the direction ofB. Find the period, the pitch `p`, and the radiusr of the helix, see figure-4.250.

View SolutionThe distance between the two plates of a cathode-ray oscilloscope is 1 cm and the potential difference between them is 1200 V. If an electron of energy 2000 eV enters at right angles to the field, what will be its deflection if the plate be 1.5 cm long.
View SolutionA solenod of length 0.4m and diametre 0.6m consists of a single layer of 1000 turns of fine wire carrying a current of `5.0xx10^-3A` . Calculate the magnetic field intensity on the axis at the middle and at the ends of the solenoid.
View SolutionA charge of 1 coul. is placed at one end of a non-conducting rod of length 0.6m. the rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency `10^(4) pi "radian/sec"`. Find the magnetic field at a point on the axis ofrotation at a distance of 0.8 from the centre of the path. Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about horizontal axis passing through the mid-point of the rod with the same angnlar frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4m form the centre of the rod.
View SolutionA long horizontal wire `P` carries of `50 A`. It is rigidly fixed. Another fine wire `Q` is placed directly above and parallel to `P`. The wieght of wire `Q` is `0.075 N//m` and carries a current of `25 A`. Find the position of wire `Q` from `P` so that the wire `Q` remains suspended due to magnetic repulsion.
View SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is `L`. A conducting massless rod of resistance `R` can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass `m` tied to the other end of the string hangs vertically. A constant magnetic field `B` exists perpendicular to the table. If the system is released from rest, calculate

a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.
View SolutionThree infinitely long thin wires, each carrying current `i` in the same direction, are in the `x-y` plane of a gravity free space . The central wire is along the `y - axis` while the other two are along `x = +-d`.
(i) Find the locus of the points for which the magnetic field `B` is zero.
(ii) If the central wire is displaced along the ` Z- direction` by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is `lambda`, find the frequency of oscillation.
View SolutionThe region between ` x=o and x = L` is filled with uniform, steady magnetic field `B_(0) hat(k)`. A particle of mass `m` , positive charge `q` and velocity `v_(0) hat(i)` travels along ` x-axis` and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of `L` if the particle emerges from the region of magnetic field with its final velocity at angle `30^(@)` to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto `2.1L`.
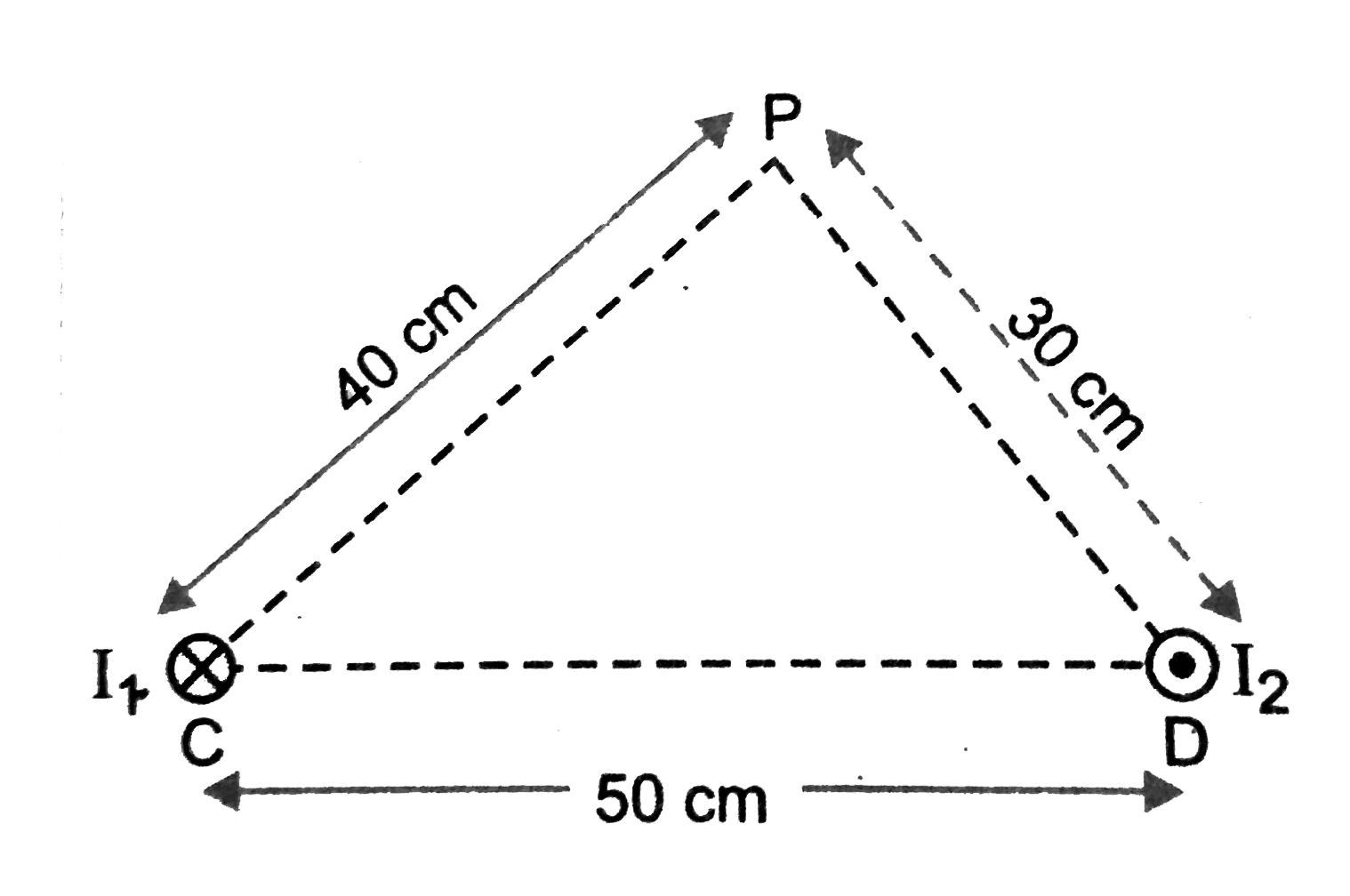
View SolutionTwo straight parallel conductors are `50cm` apart and carry oppositively directed currents, held perpendicular to the plane of paper as shown in figure. The current in first conductor, `I_1=20A` and in the second conductor is `I_2=24A`. A point P is separated from the first conductor by a distance of `40cm` and the second conductor by `30cm`. Calculate the magnetic field at point P.
View SolutionIn the Bohr model of the hydrogen atom, the electron circuulates around the nucleus in a path of radius `5xx10^-11m` at a frequency of `6.8xx10^15Hz`.
a. What value of magnetic field is set up at the centre of the orbit?
b. What is the equivalent magnetic dipole moment?
View SolutionA coil carrying a current `10mA` is placed in a uniform magnetic field so that its axis coincides with the field direction. The single layer winding of the coil is made of copper wire with diameter `0*1mm`, radius of turns is equal to `30mm`. At what value of the induction of the external magnetic field can the coil winding be ruptured? Breaking stress is `3*1xx10^8Nm^-2`.
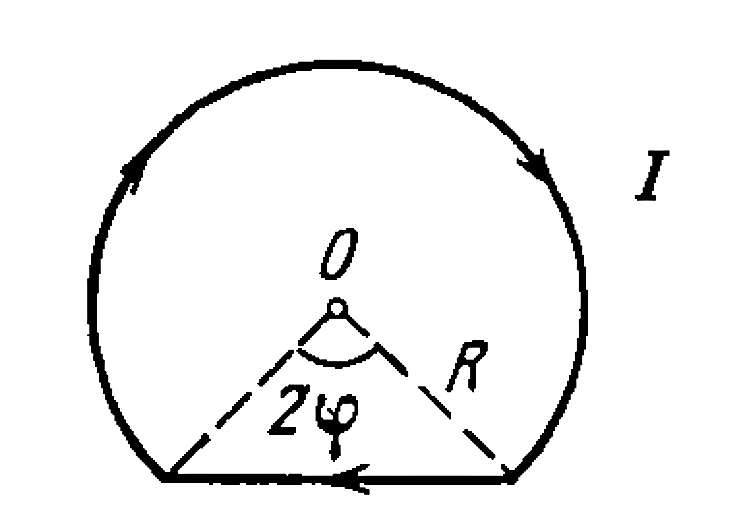
View SolutionA current `I = 5.0 A` A flows along a thin wire shaped as shwon in Fig. The radius of a curved part of the wire is equal to `R = 120 mm`, the angle `2varphi = 90^(@)`. Find the magentic induction of the field at the point `O`.
View SolutionIn an electromagnetic pump designed for transferring molten metals a pipe section with metal is located in unifrom magnetic field of induction `B` (Fig) A curent `I` is made to flow across this pipe section in the direaction perpendicular both to the vector `B` and to the axis of the pipe. FInd the gauge pressure produced by the pump if `B = 0.10T, l = 100 A`, and `a = 2.0 cm`,

View SolutionA current `I` flows in a long thin walled cylinder of radius `R`. What pressure do the walls of the cylinder experience ?
View SolutionAt the moment `t = 0` on electron leaves one plate of a parallel-plate capacitor with a neglible velocity. An accelerting volatage, varrying as `V = at`, where `a = 100 V//s` is applied between the plates is `l = 5.0 cm`. What is the velocity of the of the electron at the moment it reaches the opposite plate?
View SolutionA non-relativistic proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic fields with `E= 120 kVm^-1 and B=50 mT.` Then the beam strikes a grounded target. Find the force which the beam acts on the target if the beam current is equal to `i=0.8 mA`.
Mass of protons `= 1.67xx10^(-27) kg`.
View SolutionA proton accelarted by a potential differnce `V` gets into the unifrom electric field of a paralallel-plate capacitor whose plates extended over a length `l` in the motion direction. The field strenth varies with time as `E = at`, where `a` is a constant. Assuming the proton to be non-relatistic, find the angle between the motion directions of the proton before and after its fight throgh the capacitor, the proton gets in the field at the moment `t = 0`. The edge effects are to be neglected.
View SolutionA charged particle moves along a circle of radius `r = 100 mm` in a unifrom magnetic field with induction `B = 10.0 mT`. Find its velocity and perios of revolution if that particle is
(a) a non-relativistic proton,
(b) a relativistic electron.
View SolutionA non-relativistic charge q of mass m originates at a point A lying on x-axis and moves with velocity v at an angle to the x-axis. A screen is located at a distance l from A. Find the distance r from the x-axis to the point on the screen into which the charge strikes.

View SolutionA non-relativistic charged particle files through the electric field of a cyclindrical capacitor and gets into a unifrom transverse magnetic field with induction `B`(fig). In the capacitor the particle moves along the are of a circle, in the magnetic field, along a semi-circle of radius `r`. The potential differnce applied to the capacitor is equal to `V`, the radii of the electrodes are equal to `a` and `b`, with `a lt b`. Find the velocity of the particle and its specific charge `q//m`.
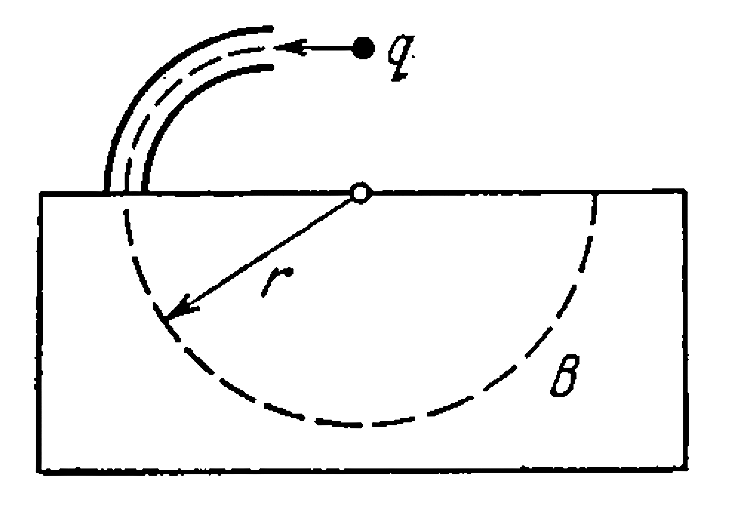
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge `q//m` leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity `v_0`

The angle `alpha` between the particle's velocity vector and y-axis at and moment is
View SolutionA narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are uniform parallel electric and magnetic fields with strengths `E and B`, at the point O. The beam direction coincides with the x-axis at the point O. A plane screen oriented at right angles to the x-axis is located at a distance `I` from O. Find the equation of trace that the ion leaves on the screen. Demonostrate that at `z lt lt l`, it is the equation of a parabola.
View SolutionA beam of non-relativistic charged particles moves without deviation through the region of space `A` where there are transverse mutually perpendicular electric and magnetic fields with strength E and induction B. When the magnetic field is switched off, the trace of the beam on the screen S shifts by `Delta x`. Knowing the distance a and b, find the specific charge q/m of the particles.
View SolutionAn electron is accelerated through a `PD` of `100 V` and then enters a region where it is moving perpendicular to a magnetic field `B=0.2T`. Find the radius of the circular path. Repeat this problem for a proton.
View SolutionA proton, a deutron and `alpha`-particle, whose kinetic energies are same, enter perpendicularly a uniform magnetic field. Compare the radii of their circualr paths.
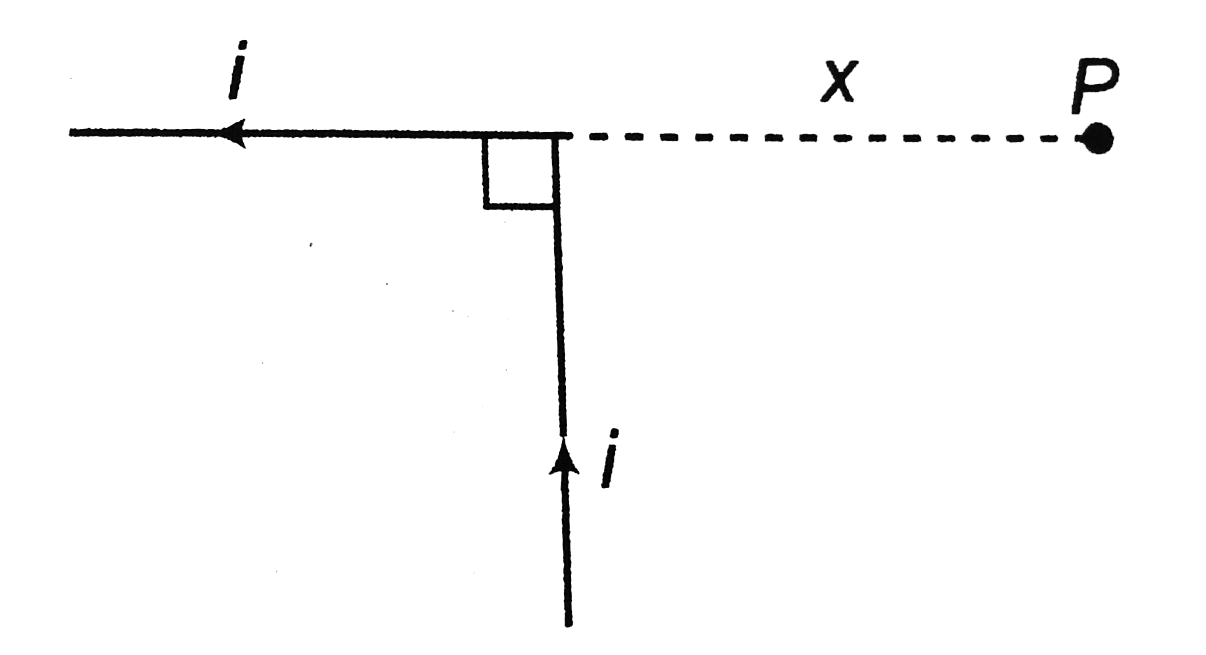
View SolutionDetermine the magnetic field at point `P` located a distance `x` from the corner of an infinitely long 2. Wire bent at right angle as shown in figure. The wire carries a steady current i.
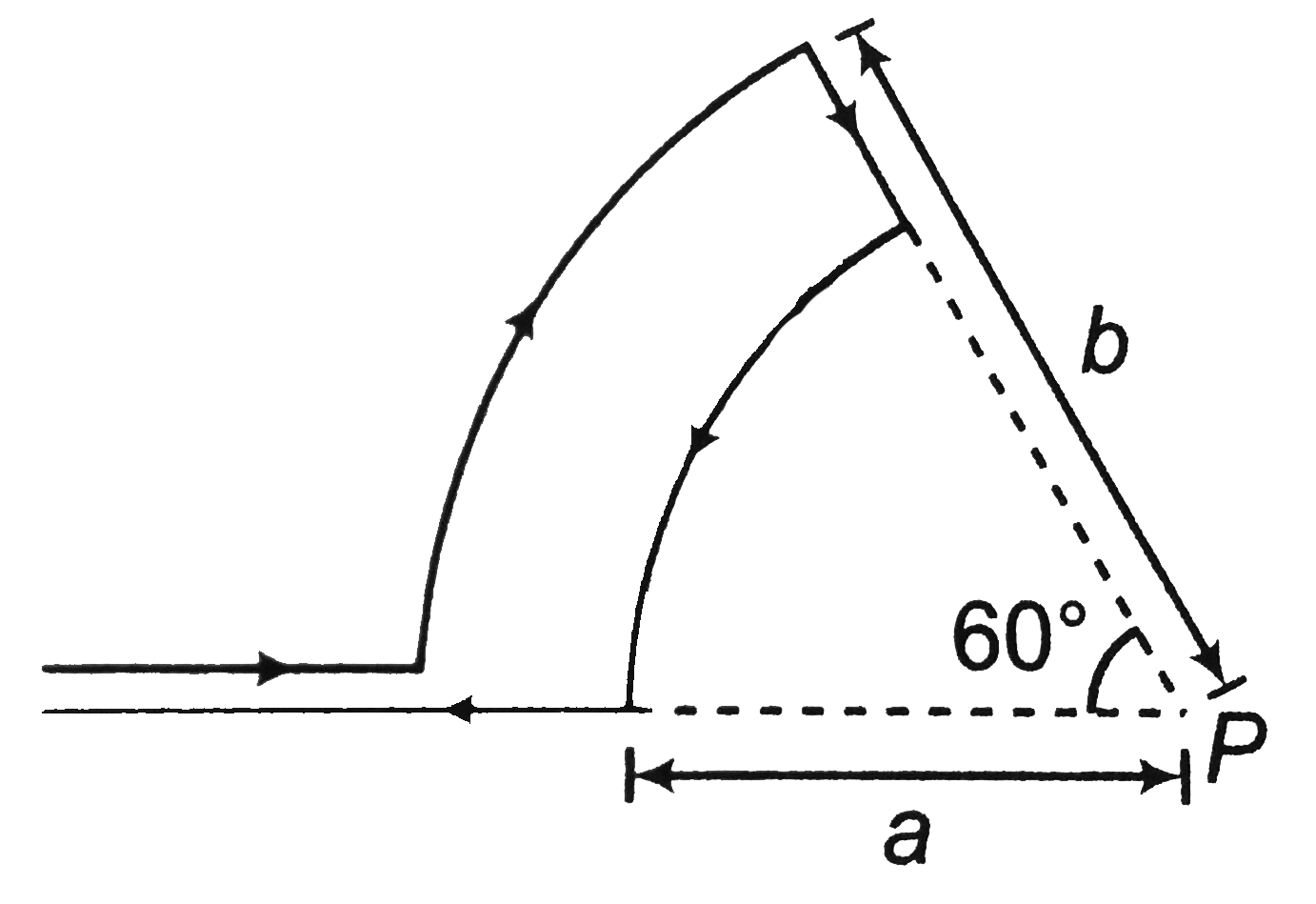
View SolutionConsider the current carrying loop shown in figure formed of radial lines and segments of circles whose centres are at point `P`. Find the magnitude and direction of B at point P.
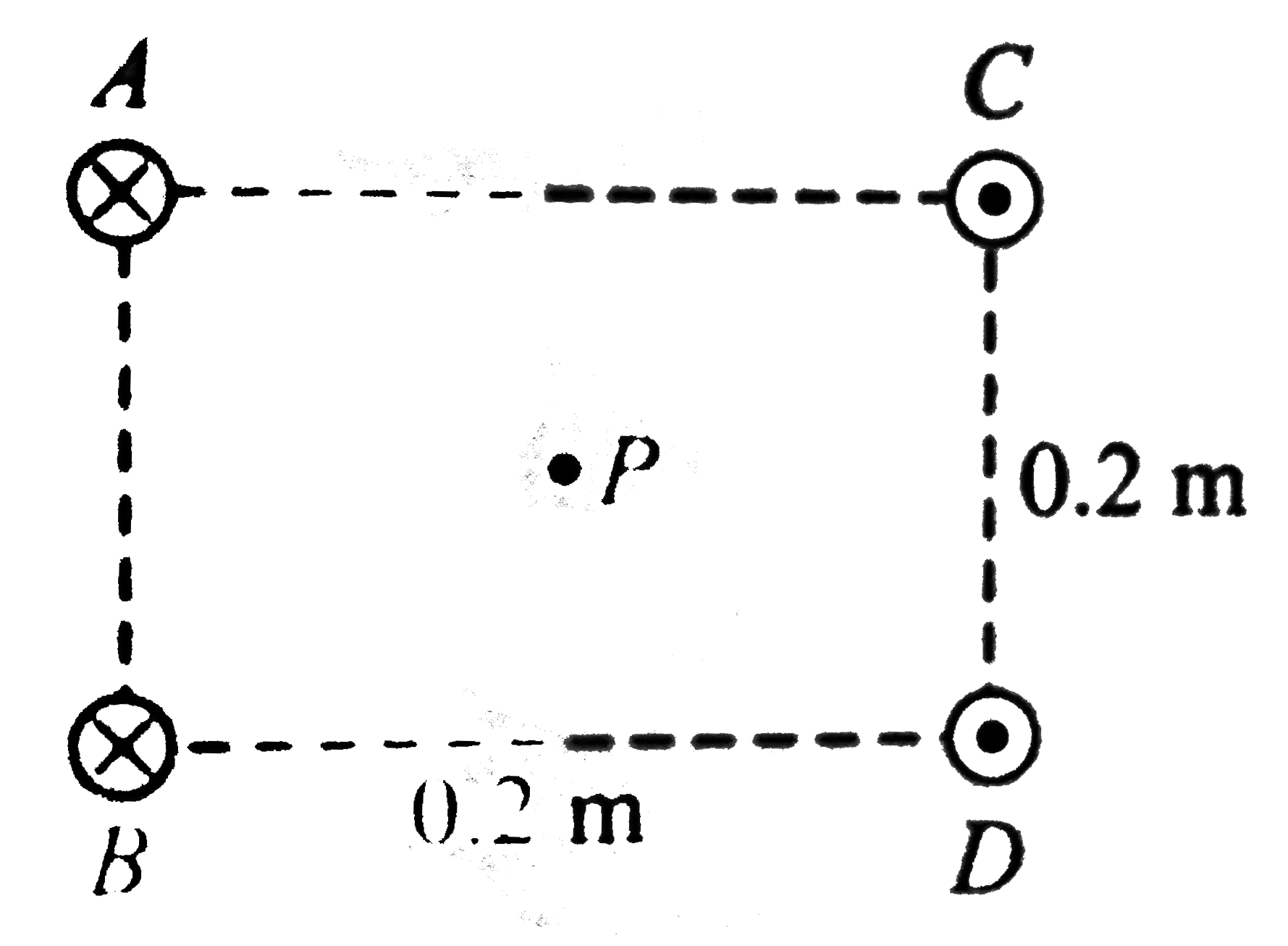
View SolutionFour long, parallel conductors carry equal currents of 5.0A. The direction of the currents is into the page at point A and B and out of the page at C and D. Calculate the magnitude and direction of the magnetic field at point P, located at the centre of the square.
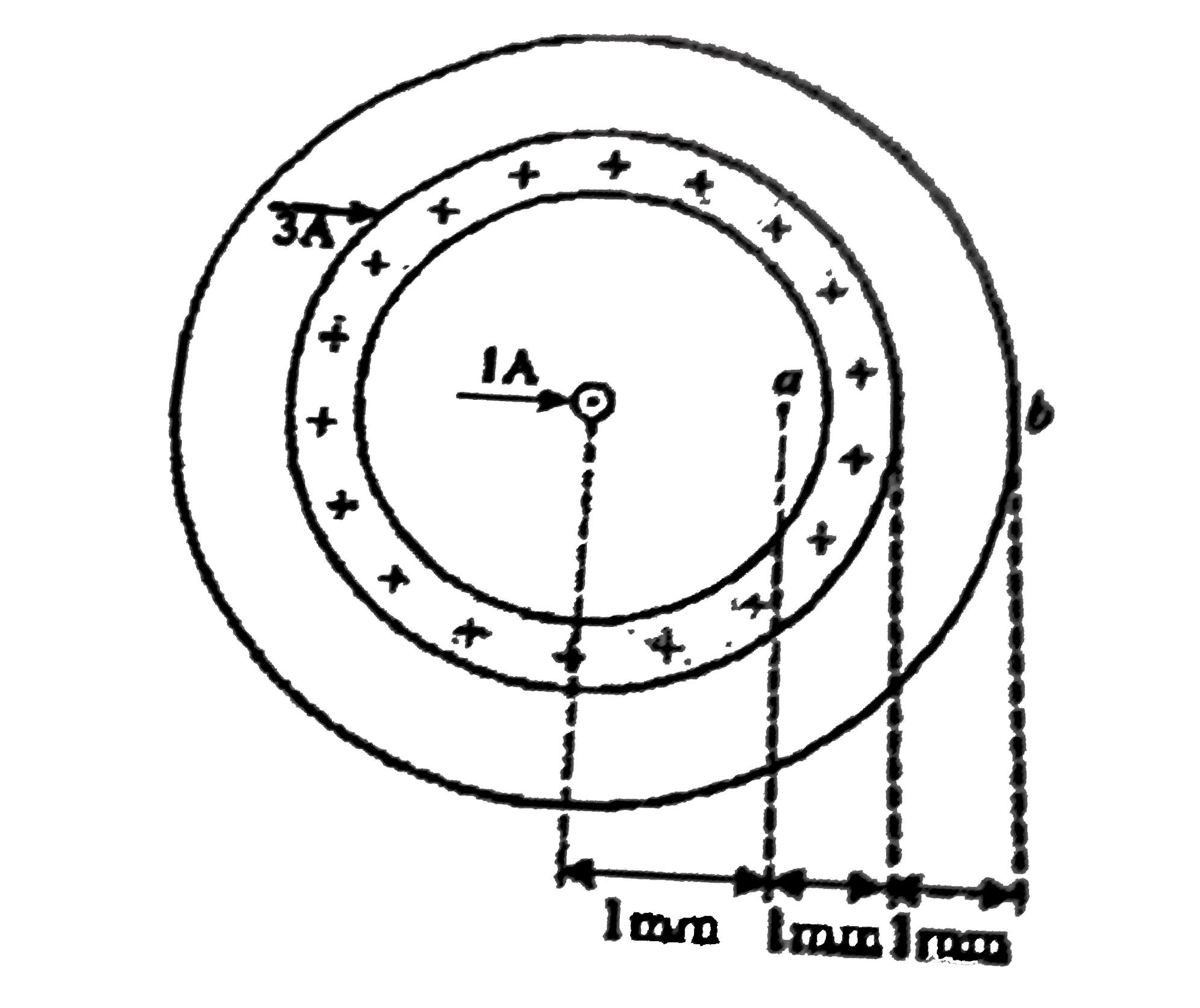
View SolutionFigure given in the question is a cross-sectional view of a coaxial cable. The centre conductor is surrounded by a rubber layer, which is surrounded by an outer conductor, which is surrounded by another rubber layer. The current in the inner conductor is `1.0 A` out of the page, and the current in the outer conductor is 3.0A into the page. Determine the magnitude and direction of the magnetic field at points a and b.
View SolutionA galvanometer coil `5 cm xx 2 cm` with 200 turns is suspended vertically in a field of `5 xx 10^-2 T`. The suspension fibre needs a torque of `0.125 x10^-7 N -m` to twist it through one radian. Calculate the strength of the current required to be maintained in the coil if we require a deflection of `6^@`.
View SolutionA charged particle carrying charge `q=1muc` moves in uniform magnetic with velocity `v_1=10^6m//s` at angle `45^@` with `x`-axis in the `xy`-plane and experiences a force `F_1=5sqrt2mN` along the negative `z`-axis. When te same particle moves with velocity `v_2=10^6m//s` along the `z`-axis it experiences a force `F_2` in `y`-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnitude of the force `F_2`.
View SolutionA wire shaped to a regular hexagon of side `2 cm` carries a current of `2A`. Find the magnetic field at the cetre of the hexagon.
View SolutionThree infinitely long thin wires, each carrying current `i` in the same direction, are in the `x-y` plane of a gravity free space . The central wire is along the `y - axis` while the other two are along `x = +-d`.
(i) Find the locus of the points for which the magnetic field `B` is zero.
(ii) If the central wire is displaced along the ` Z- direction` by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is `lambda`, find the frequency of oscillation.
View SolutionUniform electrlc and magnetic fields with strength E and B are directed along of y-axis. A particle with specific charge `q/m` leves the origin in the direction of x-axis with an initial velocity `v_0`. Find
a. the y-coordinate of the particle when it crosses the y-axis for nth time.
b. the angle `alpha` between the particle's velocity vector and the y-axis for nth time
View SolutionA particle of mass m and charge + q is projected from origin with velocity `vec(V)=V_(0)hati` in a magnetic field `vec(B)=-(B_(0)x)hatk.` Here `V_(0)` and `B_(0)` are positive constants of proper dimensions. Find the radius of curvature of the path of the particle when it reaches maximum positive x co-ordinate.
View SolutionA electron moves through a uniform magnetic field given by `vec(B)=B_(x) hat(i)+(3B_(x))hat(j)`. At a particular instant, the electron has the velocity `vec(v)=(2.0 hat(i) +4.0 hat(j))m//s` and magnetic force acting on it is `(6.4 xx 10^(-19)N)hat(k)`. Find `B_(x)`.
View SolutionA neutral particle is at rest in a uniform magnetic field `B`. At time `t = 0` it decays into two charged particles, each of mass `m`.
(a) If the charge of one of the particles is `+q`, what is the charge of the other?
(b) The two particles move off in separate paths, both of them lie in the plane perpendicular to `B`. At a later time, the particles collide. Express the time from decay until collision in terms of `m, B` and `q`.
View SolutionEach of the lettered points at the corners of the cube as shown in Fig. 1.60 represents a positive charge q moving with a velocity of magnitude v in the direction indicated. The region in the figure is in a uniform magnetic field `vec B`, parallel to the x-axis and directed toward right. Copy the figure, find the magnitude and direction of the force on each charge and show the force in your diagram.

View SolutionA proton of charge `e` and mass `m` enters a uniform magnetic field `B = Bi` with an initial velocity `v=v_xhati+v_yhatj`. Find an expression in unit vector notation for its velocity at time `t`.
View SolutionA thin, `50.0 cm` long metal bar with mass `750 g` rests on, but is not attached to, two metal supports in a `0.450 T` magnetic field as shown in figure. A battery and a resistance `R = 25.0Omega` in series are connected to the supports.
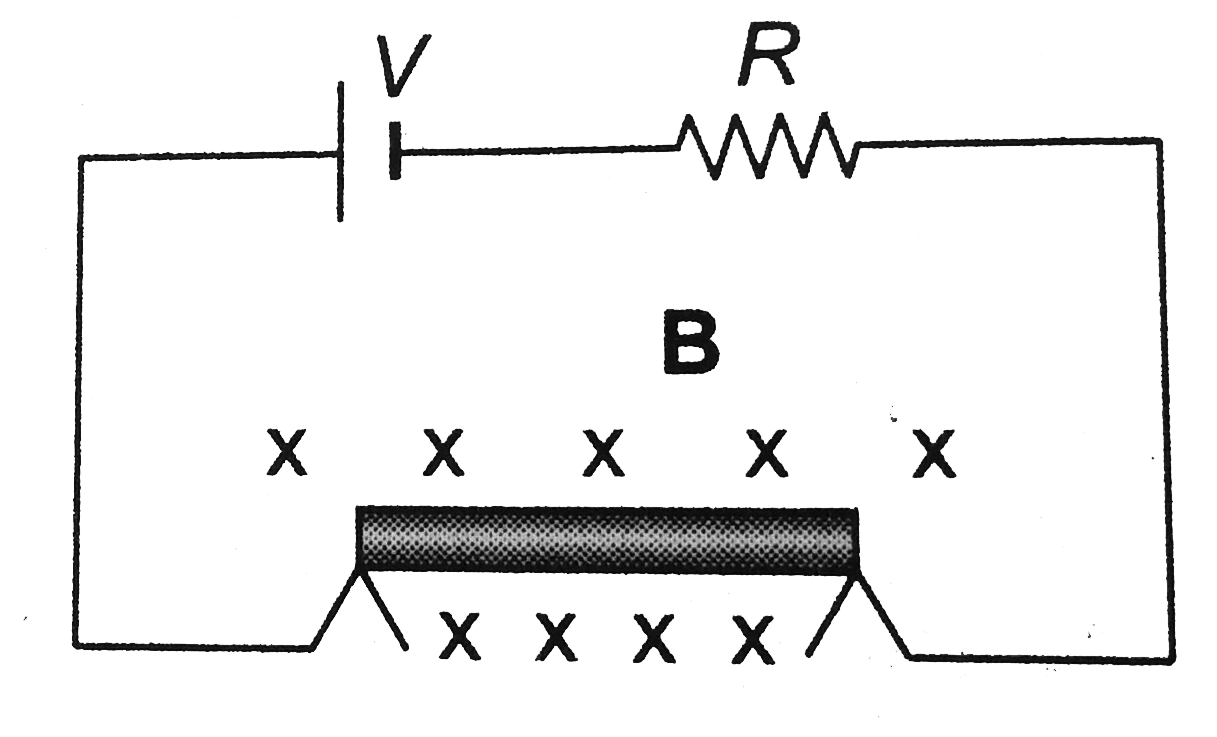
(a) What is the largest voltage the battery can have without breaking the circuit at the supper
(b) The battery voltage has this maximum value calculated. Decreasing the resistance to `2.0 Omega` the initial acceleration of the bar.
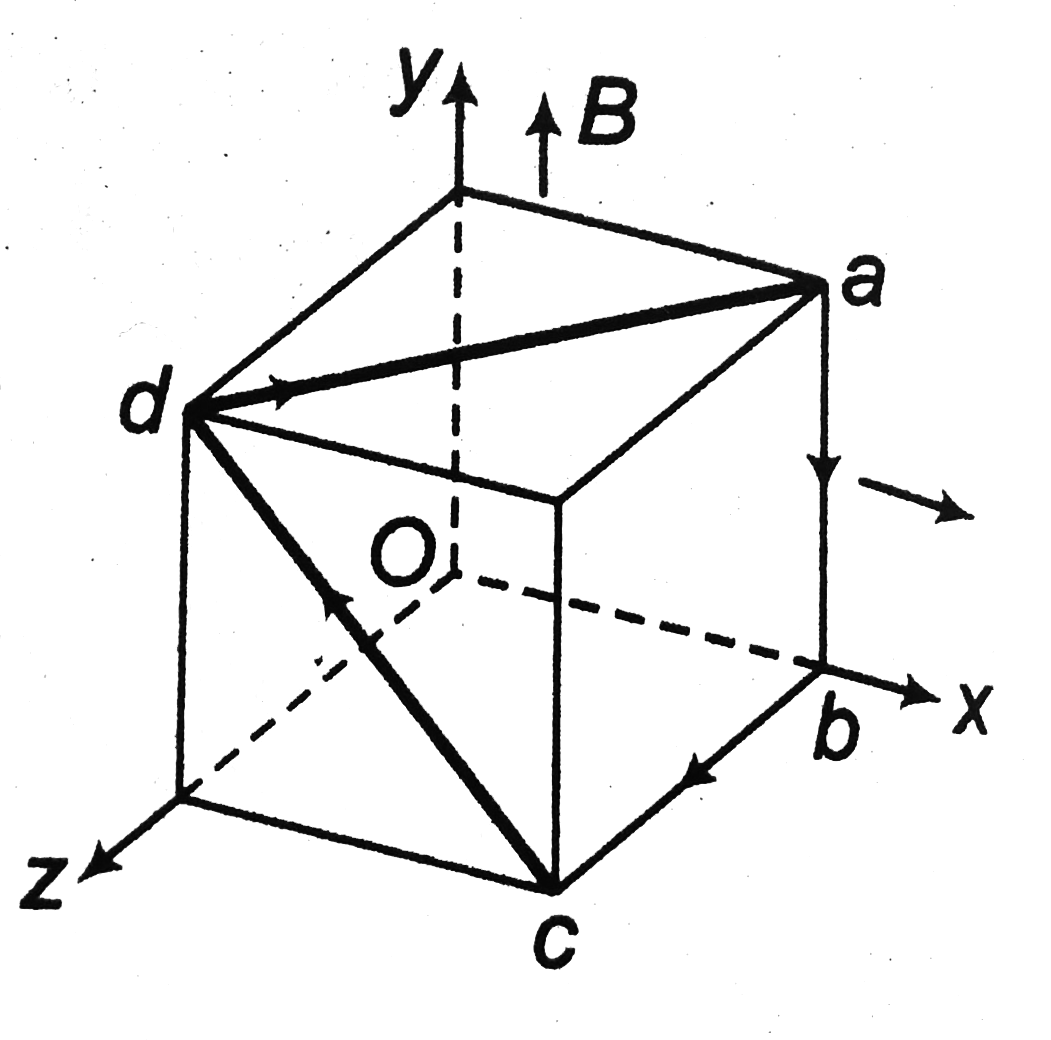
View SolutionIn figure, the cube is `40.0 cm` on each edge. Four straight segments of wire `ab, bc, cd` and `da` form a closed loop that carries a current `I=5.00A`, in the direction shown. A uniform magnetic field B magnitude the positive y-direction. Determine the magnitude and `B =0.020 T` is in direction of the magnetic force on each segment.
View SolutionA length `L` of wire carries a current `i`. Show that if the wire is formed into a circular coil, then the maximum torque in a given magnetic field is developed when the coil has one turn only, and that maximum torque has the magnitude `tau=L^2iB/4pi`
View SolutionA coil with magnetic moment `1.45 A -m^2` is oriented initially with its magnetic moment antiparallel to a uniform `0.835 T` magnetic field. What is the change in potential energy of the coil when it is rotated `180^@` so that its magnetic moment is parallel to the field?
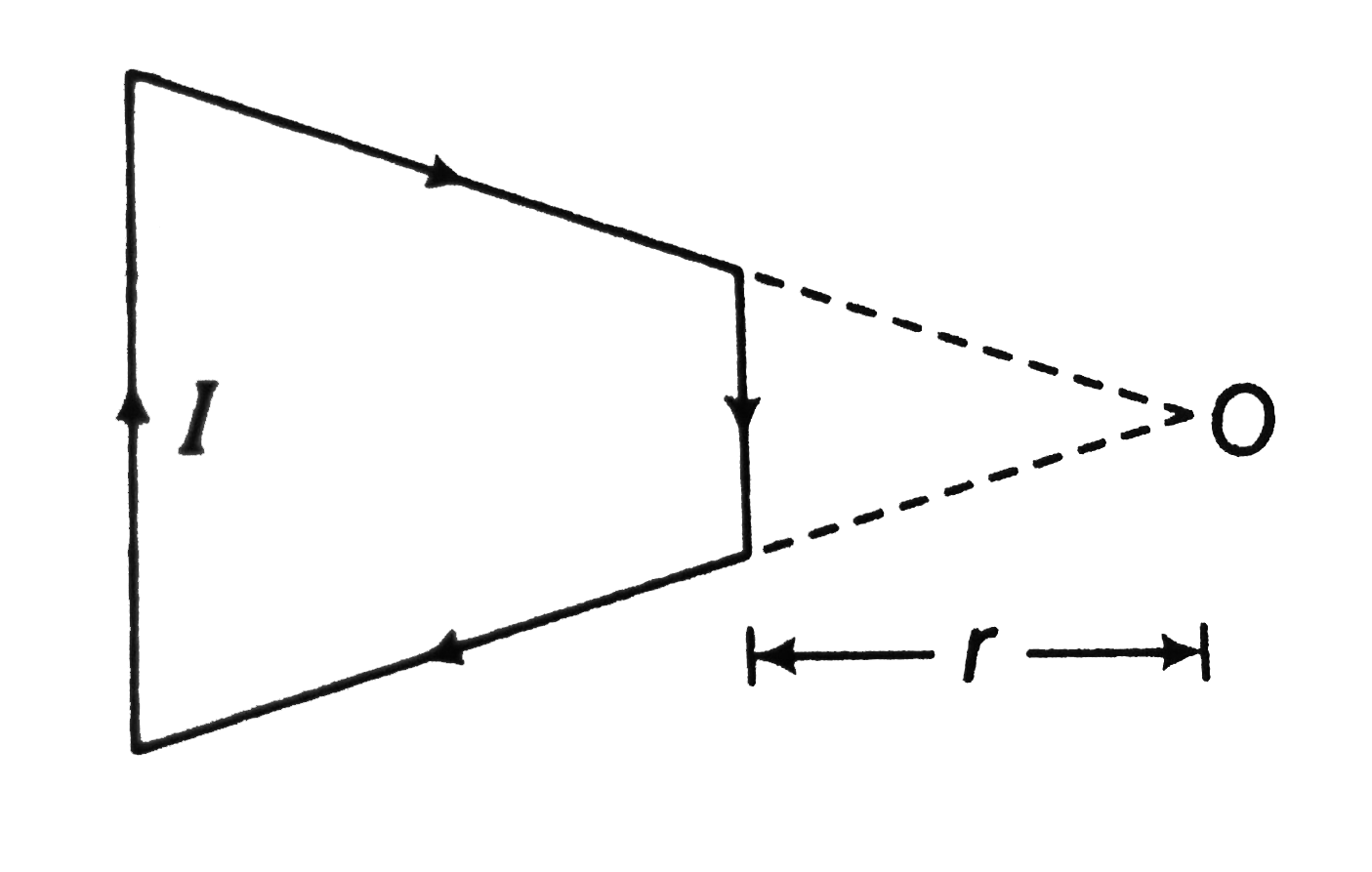
View SolutionA current `I = sqrt2` A flows in a circuit having the shape of isosceles trapezium. The ratio of the bases of the trapezium is 2. Find the magnetic induction B at symmetric point O in the plane of the trapezium. The length of the smaller base of the trapezium is `100 mm` and the distance `r=50mm`.
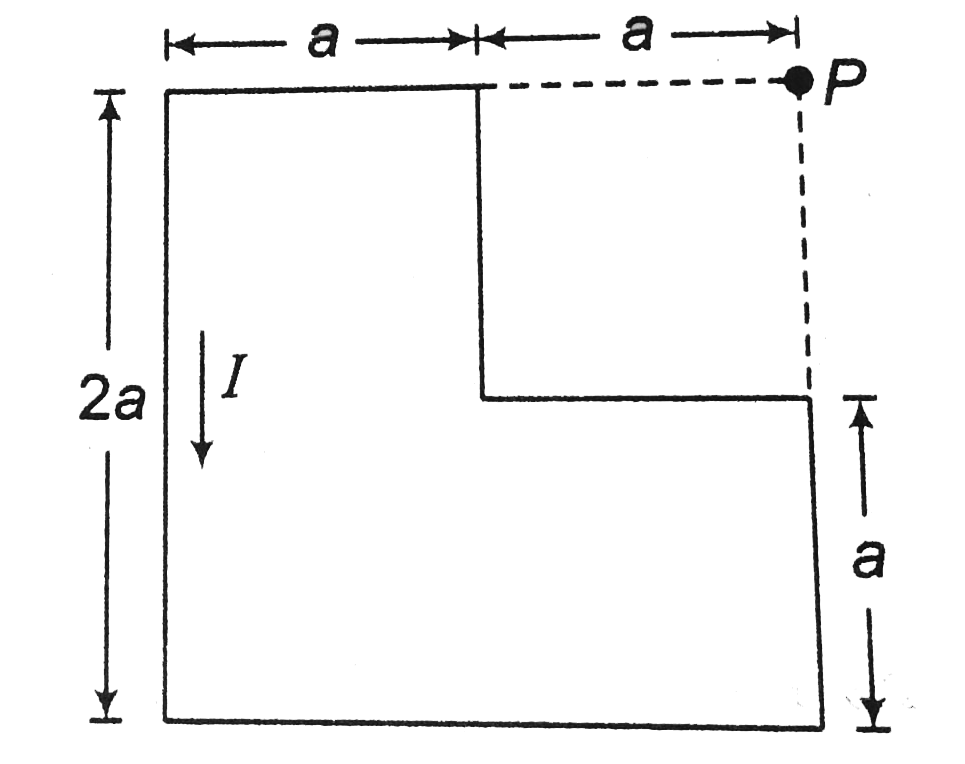
View SolutionFind the magnetic field `B` at the point `P` in figure
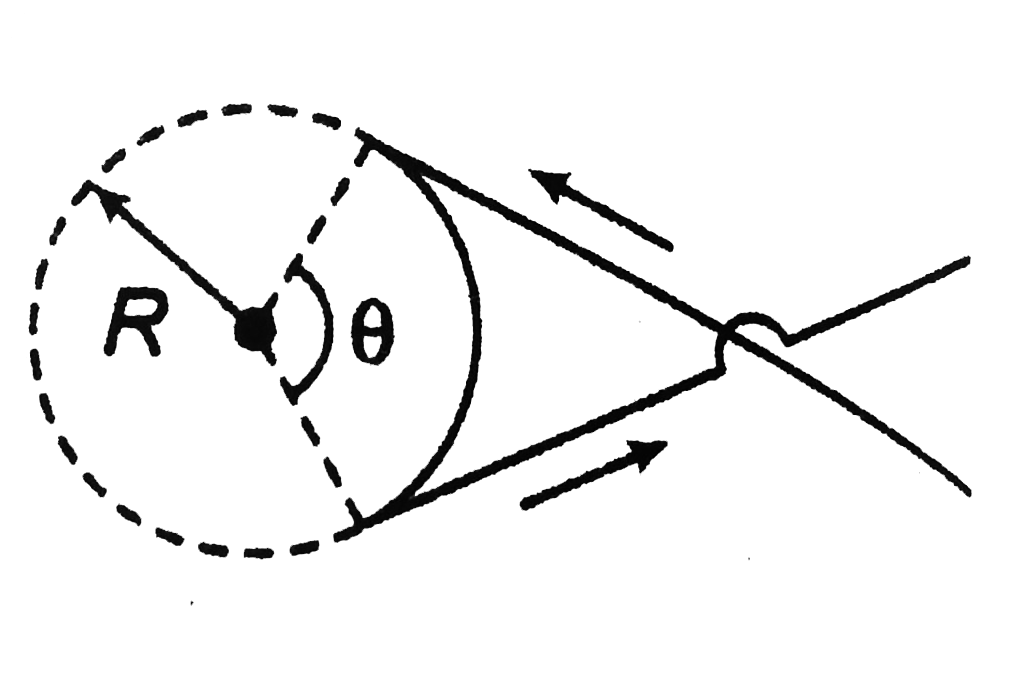
View SolutionA wire carrying current `i` has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must be for `B` to be zero at the centre of the circle?
View SolutionA closely wound coil has a radius of 6.00 cm and carries a current of `2.50 A`. How many turns must it have if, at a point on the coil axis `6.00 cm` from the centre of the coil, the magnetic field is `6.39 xx 10^-4T` ?
View SolutionA closed cure encircles several conductors. The line integral `intB.dI` around this curve is `3.83xx10^-7T-m`
a. What is the net current in the conductors?
b. If you were to integrate aroundthe curve in the opposite direction, what would be the value of the line integral?
View SolutionA long cylindrical conductor of radius a has two cylindrical cavities of diameter a through its entire length as shown in cross-section in figure. A current `I` is directed out of the page and is uniform throughout the cross-section of the conductor. Find the magnitude and direction of the magnetic field in terms of `mu_0,I,r` and a.
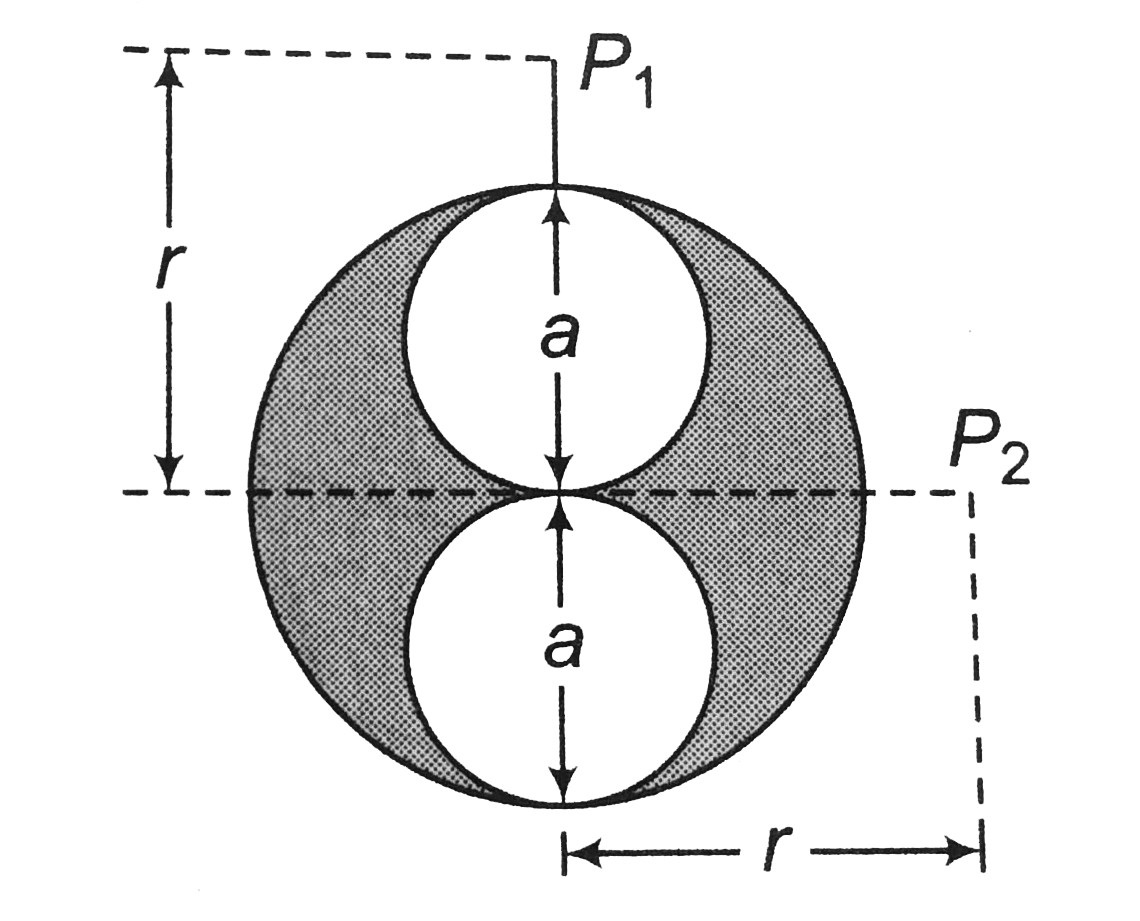
(a) at point `P_1` and (b) at point `P_2`
View SolutionTwo infinite plates shown in cross-section in figure carry `lamda` amperes of current out of thepage per unit width of plate. Find the magnetic field at points `P` and `Q`.

View SolutionA long horizontal wire `AB`, which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another parallel long wire `CD` which is fixed in a horizontal plane and carries a steady current of ` 30 A`, as shown in figure. Shown that when `AB` is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.

View SolutionA magnet of length `0.1 m` and pole strength `10^(-4)` A.m. is kept in a magnetic field of `30 Wb//m^(2)` at an angle `30^(@)`. The couple acting on it is `…xx10^(-4)Nm`.
View SolutionThe force experienced by a pole of strength 100 Am at a distance of 0.2 m from a short magnet of length 5 cm and pole strength of 200 Am on its axial line will be
View SolutionA manetic needle is suspended at a distance of 1m from a short magnet on the eastern side on its axial line. The deflection produced is `30^(@)`. Calculate the horizontal component of earth's magnetic field if the magnetic moment of the magnet is `100 Am^(2)`
View SolutionA coil in the shape of an equilateral triangle of side 0.02 m is suspended from a vertex such that it is hanging in a vertical plane between the pole pieces of a permanent magnet producing a horizontal magnetic field of `5 xx 10^(-2) T.` Find the couple acting on the coil when a current of 0.1 A is passed through it and the magnetic field is parallel to its plane.
View SolutionA vibraiton magnetometer consits of two idential bar magnets placed one over the other such that they are mutually perpendicular and bisect each other. The time period of oscillations of combination in a horizontal magnetic field is `4s`. If one of the magnets is removed, then the period of oscillations of the other in teh same field is
View SolutionA small magnet of magnetic moment `pixx10^(-3) Am^(2)` is placed on the Y-axis at a distance of 0.1 from the origin with its axis parallel to the X-axix. A coil have 169 turns and radius 0.05 m is placed on the X-axis at a distance of 0.12 m from the origin with the axis of the coil coinciding with the X-axis. Find the magnitude and direction of the current in the coil for a compass needle placed at the origin, to point in the north-south direction.
View SolutionA circular of radius 0.157 m has turns. It is placed such that its axis is in magnetic meridian. A dip needle is supported at the centre of the coil with its axis of rotation horizontal, and in the plane of the coil. The angle of dip is `30^(@)` when a current flows through the coil. The angle of dip becomes `60^(@)` on reversing the current. Find the current in the coil assuming that the magnetic field due to the coil is smaller than the horizontal component of earth's magnetic field, `H =3xx10^(-5) T`.
View SolutionA small magnet of magnetic moment M is placed at broad side on position of a magnet of magnetic M', length 2l' in such a way that the axis of former coincides with the perpendicular bisector of the latter. The separation between their centres is d. Calculate the nature of interaction (force or couple ) among them. What is its limiting value, when d becomes very large ?
View SolutionA small coil of radius 0.002 m is placed on the axis of a magnet of magnetic moment `10^(5)` `JT^(-1)` and length 0.1 m at a distance of 0.15 m from the centre of the magnet. The plane of the coil is perpendicular to the axis of the magnet. Find the force on the when a current of 2.0 A is passed through it.
View SolutionA magnet is suspended in the magnetic meridian with an untwisted wire. The upper end of wire is rotated through `180^(@)` to deflect the magnet by `30^(@)` from magnetic meridian. When this magnet is replaced by another magnet, the upper end of wire is rotated through `270^(@)` to deflect the magnet `30^(@)` from magnetic meridian. The ratio of magnetic moment of magnets is
View SolutionA coil of 50 turns and 10cm diameter is made out of a wire of resistivity `2 xx 10^(-6) Omega cm` and cross sectional radius 0.1mm. The coil is connected to a source of EMF `10 V` and of negligible internal resistance.
(a) Find the current through the coil
(b) What must be potential difference across the coil so as to nullify the horizontal component of earth's magnetic field, `0.314 xx 10^(-4) T` at the centre of the coil. How should the coil be placed to achieve. this result?
View SolutionA Rowland ring of mean radius 15 cm has 4500 turns of wire wound on a ferromagnetic core of relative permeability 800. Find the magnitnde of the magnetic field in the core for a magnetising current of 1.2 A.
View SolutionA magnet is suspended at an angle `60^(0)` in an external magnetic field of `5xx10^(-4)T`. What is the work done by the magnetic field in bringing it in its direction? `["The magnetic moment"=20A-m^(2)]`
View SolutionThe time period of a bar magnet oscillating in a uniform magnetic field is 3 seconds. if the magnet is cut into two equal parts along the equatorial line of the magnet and one part is made to vibrate in the same field, what is the time period ?
View SolutionA small coil of radius 0.002 m is placed on the axis of a magnet of magnetic moment `10^(5)` `JT^(-1)` and length 0.1 m at a distance of 0.15 m from the centre of the magnet. The plane of the coil is perpendicular to the axis of the magnet. Find the force on the when a current of 2.0 A is passed through it.

View SolutionFind the interaction energy of two loops carrying currents `I_(1)` and `I_(2)` if both loops are shaped as circles of radii `a` and `b`, with `a lt lt b`. The loops centres are located at the same point and their planes from an angle `theta` between them.
View SolutionAn electron accelerated by a potential difference `V=1.0 kV` moves in a uniform magnetic field at an angle `alpha = 30^@` to the vector B whose modulus is `B=29 mT.` Find the pitch of the helical trajectory of the electron.
View SolutionA particle accelerated by a potential difference `V` flies through a uniform transverse magnetic field with induction B. The field occupies a region of space din thickness. Prove that the angle a through which the particle deviates from the initial direction of its motion is given by.
`alpha=sin^(-1)(dBsqrt((q)/(2 Vm)))`
where `m` is the mass of the particle.
View SolutionA beam of electrons enters a uniform magnetic field of `0*3T` with a velocity of `4xx10^5ms^-1` at an angle of `60^@` to the field. Find the radius of the helical path taken by the beam. Also find the pitch of the helix (distance travelled by a proton parallel to the magnetic field during one period of rotation). Mass of proton is `1*67xx10^(-27)kg`.
View SolutionA particle of mass m and charge q is moving in a region where uniform, constant electric and mangetic fields `vec E and vec B` are present. `vec E and vec B` are parallel to each other. At time `t=0,` the velocity `vec v_0` of the particle is perpendicular to `vec E` (Assume that its speed is always `lt lt c`, the speed of light in vacuum). Find the velocity `vec v` of the particle at time `t`. You must express your answer in terms of `t, q, m,` the vector `vec v_0, vec E` and `vec B` and their magnitudes `vec v_0, vec E` and `vec B`.
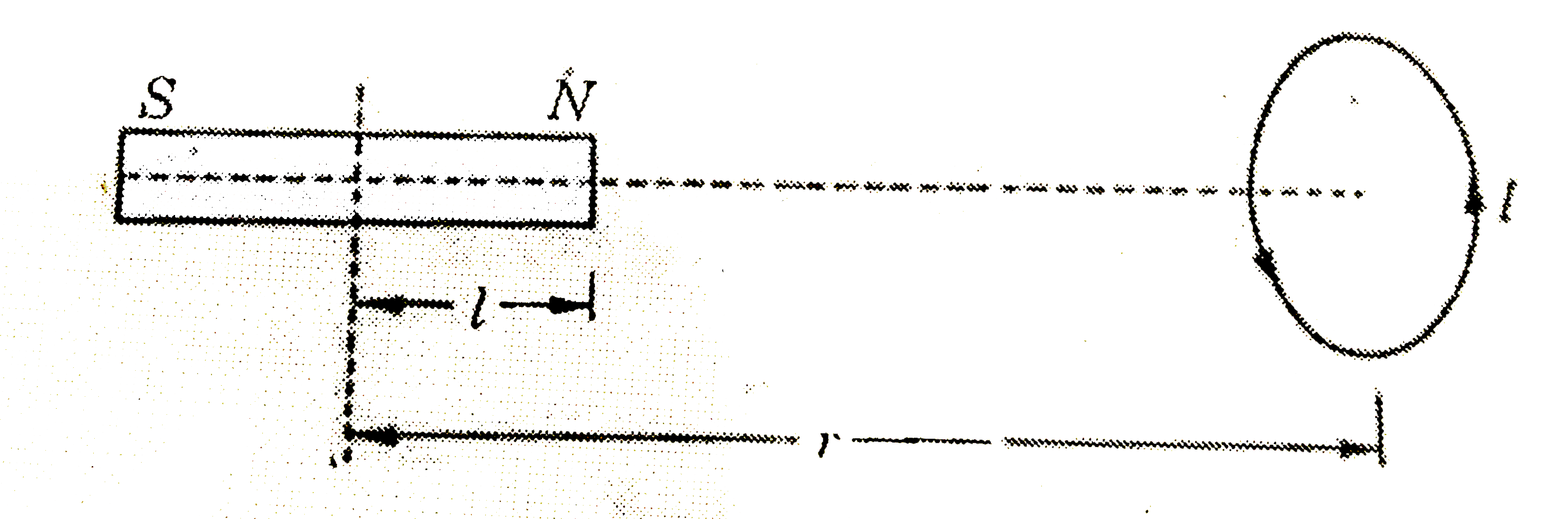
View SolutionA uniform magnetic field with a slit system as shown in Fig. is to be used as a momentum filter for highenergy charged particles. With a field B tesla, it is found than the filter transmits `alpha` each of energy 5.3MeV. The magnetic field is increased to 2.3 tesla and deuterons are passed into the filter. The energy of each deutrons are passed into the filter. The energy of each deutrons transmitted by the filter is ........... MeV.

View SolutionA deflection of 24 divisions ofa ballistic galvanometer is obtained either by charging a capacitor of `3 mu F` capacitance to a potential difference of `2V` and discharging through the galvanometer or by connecting the ballistic galvanometer in series with a flat circular coil of 80 turns, each of diameter 1cm, the combined resistance of coil and galvanometer being 4000 ohm and quickly thrusting the coil into a strong magnetic field so that the plane of the coil is perpendicular to the direction of the field. Calculate the sensitivity of the galvanometer and calculate the strength of the magnetic field. The strength of the earth's magnetic field may be neglected.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is `R` and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View Solution
U.N.P questions and complete solutions for chapter MAGNETIC EFFECTS OF CURRENT AND MAGNETISM of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12