Complete Solutions to Solved Examples of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| PRADEEP | Solved Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What is the current flowing through a conductor if 1 million electrons are crossing in 1 millisecond through a cross section of it from A to B ? Charge on an electron `=1 .6 xx 10^(-19) C`.
View Solution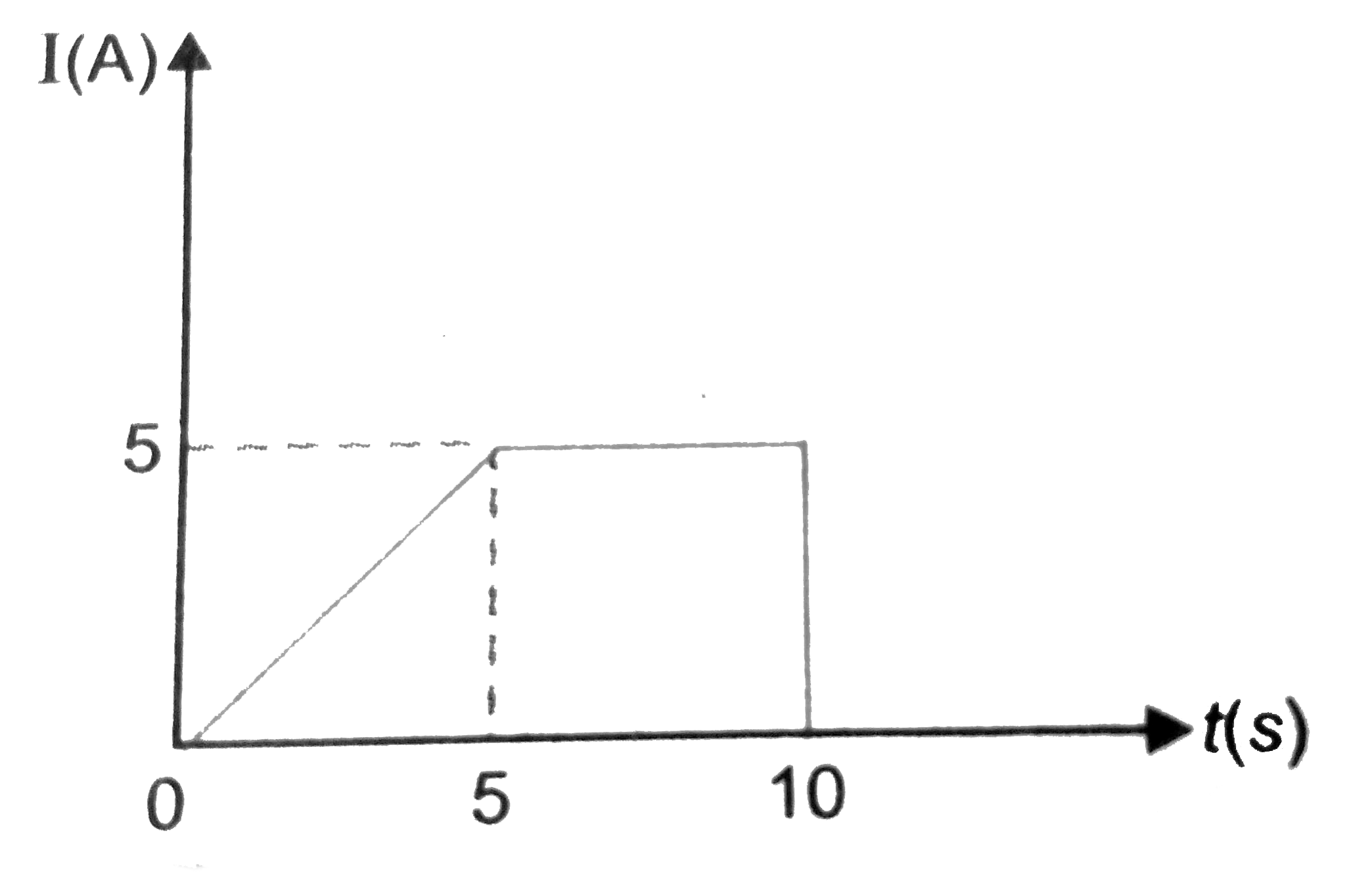 shows a plot of current `I` through the cross-section of a wire over a time interval of 10s. Find the amount of charge that flows through the wire during this time period.
shows a plot of current `I` through the cross-section of a wire over a time interval of 10s. Find the amount of charge that flows through the wire during this time period.
View SolutionEstimate the average drift velocity of conduction electrons in a copper wire of cross-sectional area `2.5 xx 10^(-7) m^(2)`, carrying a current of 2.7 A. Assume the density of conduction electrons to be `9 xx 10^(28) m^(-3)`.
View SolutionWhat is the length of a nichrome wire of radius 0.32 mm, resistance `9.3 Omega` and resistivity `15 xx 10^(-6)Omega m` ? If a potnetial differences of 10 V is applied across the wire, what will be the current in the wire ?
View SolutionFind the conductance of a conductor of resistance 2 milli ohm.
View SolutionPotential difference of 100 V is applied to the ends of a copper wire one metre long. Calculate the average drift velocity of the electrons ? Compare it with thermal velocity at `27^@C`. Consider there is one conduction electron per atom. The density of copper is `9.0xx10^(3)kg//m^(3)`, Atomic mass of copper is 63.5 g. Avogadro's number `= 6.0 xx 10^(23)` per gram-mole. Conductivity of copper is `5.81 xx 10^(7)Omega^(-1)m^(-1)`. Boltzmann constant `= 1.38 xx10^(23)JK^(-1)`.
View SolutionThe resistance of a conductor at `30^@C` is `3.25 Omega` and at `100^@C` is `3.95Omega`. Calculate the temperature coefficient of resistance of the conductor and the resistance of the conductor at `0^@C`.
View SolutionFor the given carbon resistor, let the first strip be yellow, second strip be red, third strip be orange and fourth be gold. What its resistance?
View SolutionThe resistance of the given carbon resistor is `(24xx10^6+-5%)Omega`. What is the sequence of colours on the strips provided on resistor?
View SolutionA wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
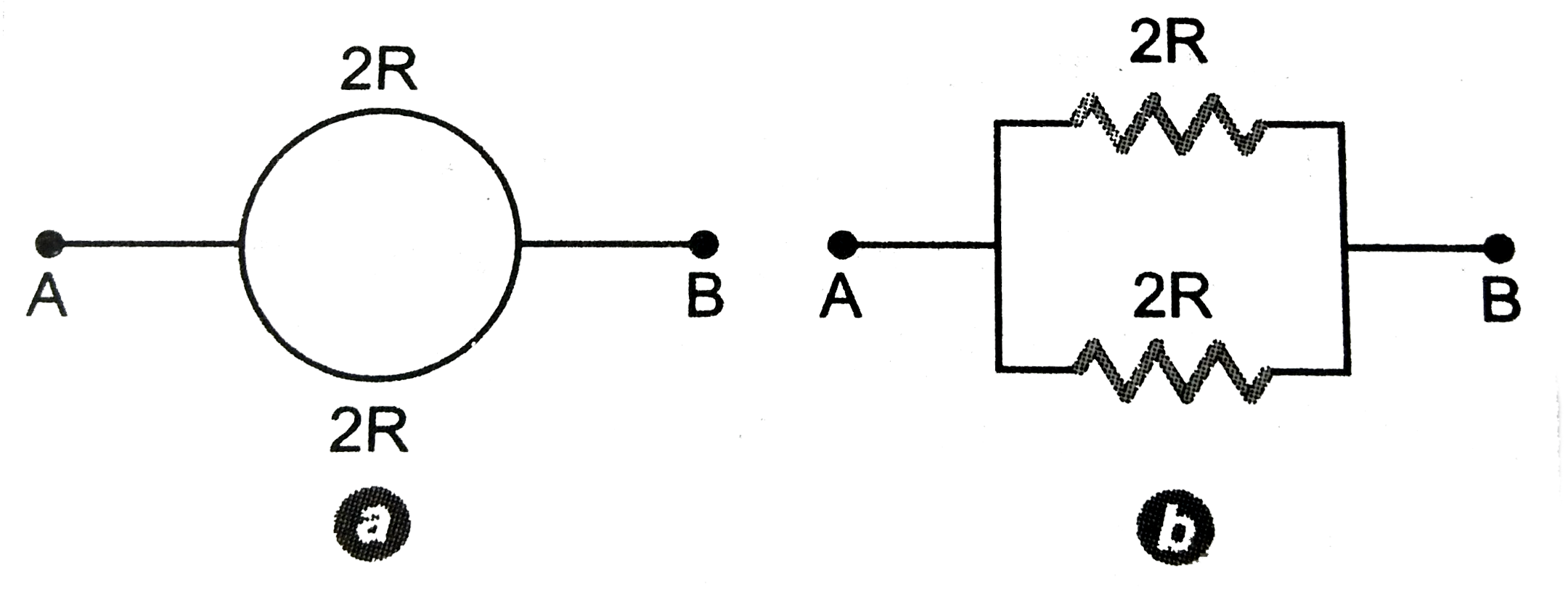
View SolutionA voltmeter of resistance `995 Omega` is connected across a cell of emf 3V and internal resistance `5 Omega`. Find the potential difference across the voltmeter, that across the terminals of the cell and percentage error in the reading of voltmeter.
View Solution45 cells each of internal resistance `0.4Omega` and emf 2.0 V are used to send current through an external circuit of resistance `2.0 Omega`. What will the best mode of grouping them for maximum current? Find the currnet in the external circuit.
View SolutionIn a Wheatstone bridge circuit, `P=5 Omega, Q=6 Omega, R=10 Omega` and `S= 5 Omega`. Find the additional resistance to be used in series with S, so that the bridge is balanced.
View SolutionA current of 1.0 mA is flowing through a potentiometer wire of length 4 m and of resistance `4 Omega`, find the potential gradient of potentiometer wire
View SolutionA bulb of `484 Omega` is producing light when connected to 200 V supply. What is the electric power of the bulb?
View SolutionHow much current is drawn by the motor of 0.5 hp from 220 volt supply?
View SolutionA bulb of 100 W is operating for 6 hours a day. Find the units of energy consumed in 7 days.
View SolutionAn electric motor operates on a 110 V supply and draws a current of 10 A. If the motor yields a mechanical power of 330 watt, what is the efficiency of the motor ?
View SolutionShow that one ampere is equivalent to flow of `6.25xx10^(-18)` elementary electrons per second ? Charge on electron `=1.6 xx 10^(-19)C`.
View SolutionHow many electrons pass through a lamp in one minute, if the current is 300 m A?
View SolutionIf `10^(6)` electrons pass from a point towards another point B in a conductor in one microsecond. Find the magnitude and direction of current. Give charge of an electron is `1.6 xx 10^(-19)` C.
View SolutionIn an atom an electron revolves around the nucleus in a circular orbit at the rate of `6xx10^(15)` revolutions per second. Calculate the equivalent current in milliampere. Take value of electromic charge `= 1.6xx10^(-19)C`.
View SolutionIn Bohr model of hydrogen atom, the electron revolves around the nucleus in a circular orbit of radius `5.0xx10^(-11)` m with a speed `2.2 xx10^(6) ms^(-1)`. Find the equivalent current. (Electronic charge = `1.6 xx 10^(-19)`coulomb)
View SolutionIn a discharge tube, the number of protons drifting across a cross-section is `1.5xx10^(18)` per second, while the number of electrons drifting in opposite direction across that cross-section is `3.0xx10^(18)` per second. Find the total current crossing the given cross- section.
View SolutionIf 0.8 mole of electrons flow through a wire in 55 minutes. What is (a) the total charge in kilocoulomb that passes through the wire and (b) the magnitude of the current? Avogadro's number `=6xx10^(23)` per mole.
View SolutionIn a conductor, `10^(16)` electrons move from a point A towards point B in 1 milli second. `10^(14)` positive ions move from a point B towards point A in 1 milli second. What is the current in ampere and its direction? Charge on electron = charge on position ion `= 1.6 xx 10^(-19)C`.
View Solution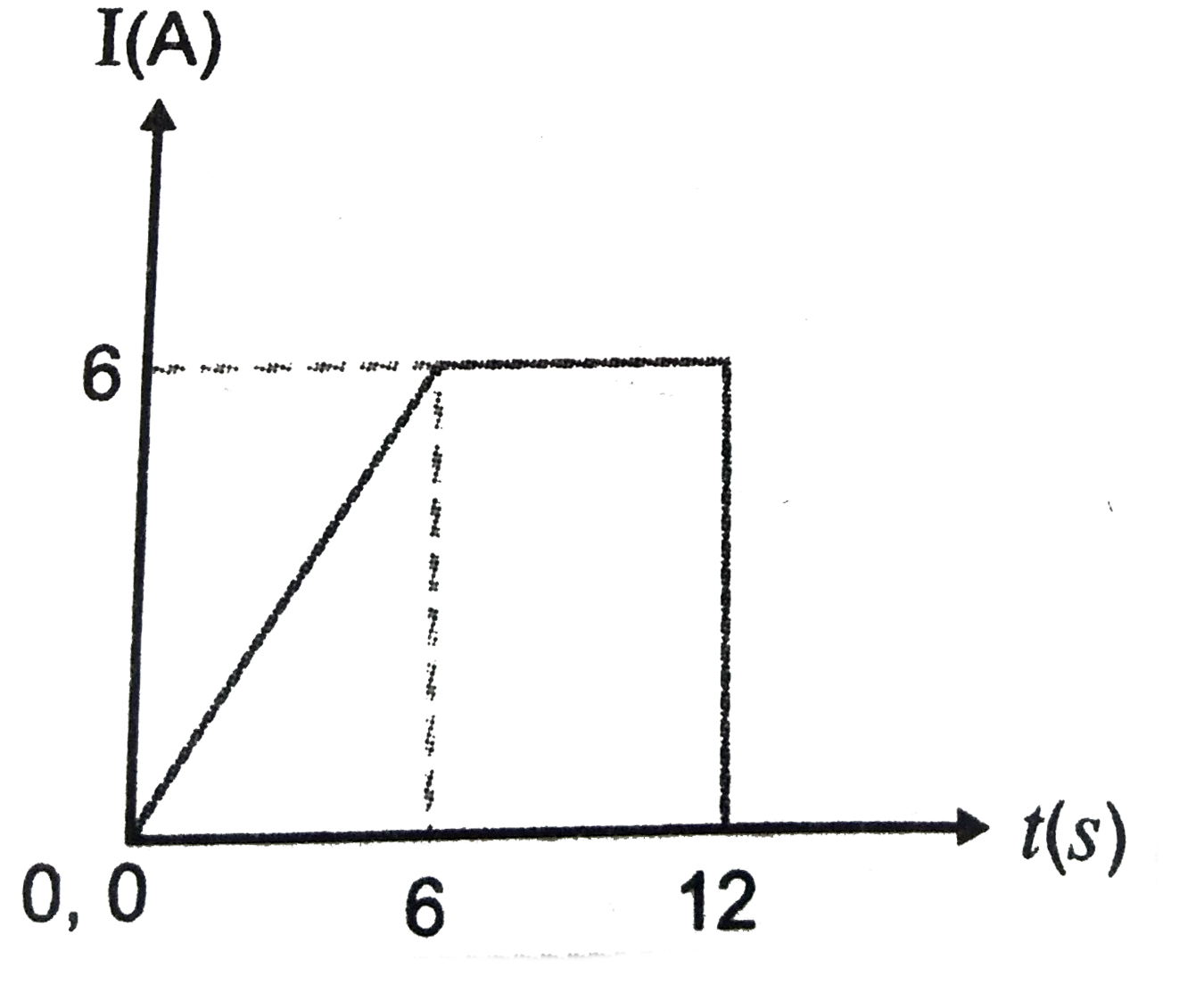
The variation of current I through the cross section of the wire over a time interval of 12 second. Find the charge that flows in this wire in 12 seconds.
View SolutionThe charge flowing in a conductor varies time as,
`q=at - 1/2 bt^(2) +1/6 ct^(3)`
Where a,b,c are positive constants. Then, find (i) the initial current (ii) the time after which the value of current reaches a maximum value (iii) the maximum or minimum value of current.
View SolutionA steady beam of `alpha`-particles travelling with kinetic energy `E=83.5 keV` carries a current of `I=0.2 mu A`. Mass of `alpha`-particle `=6.68 xx10^(-27)kg`.
(i) If this beam strikes a plane surface at an angle `theta=60^@` with normal to the surface, how many `alpha` -particles strike the surface in t=4 second?
View SolutionAt room temperature copper has free electron density of `8.4xx10^(28) per m^(3)` . The copper conductor has a cross-section of `10^(-6)m^(2)` and carries a current of 5.4 A. What is the electron drift velocity in copper?
View SolutionThe number of free electrons per 100 mm of ordinary copper wire is `2xx10^(21)`. The average drift speed of electorn is `0.25 mm//s`. What is the current flowing?
View SolutionA copper wire of diameter 1.0 mm carries a current of 0.2 A. Copper has `8.4xx10^(28)` atoms per cubic metre. Find the drift velocity of electrons, assuming that one charge carrier of `1.6xx10^(-19)` C is associated with each atom of the copper.
View SolutionA 60 coulomb of charge flows through a wire in half minute. The radius of the wire is 1 mm. The wire contains `5xx10^(22)` electrons per cubic centimetre. Calculate the current and drift velocity.
View SolutionA current of 3 A is flowing through a wire of length 2 m and cross- sectional area `1mm^(2)`. If wire contains `10^(29) "electrons"//m^(3)`, calculate the average time taken by an electron to cross the length of the wire.
View SolutionThere is a copper wire of length 2.2 m, of area of cross-section 2.0sq.mm, carrying a current of 6.0A. If the number density of electrons in copper is `8.5 xx10^(28) m^(-3)`, find the time taken by an electron to drift from one end to another end of the wire.
View SolutionIf the free electron density of copper is `8.6xx10^(28)m^(-3)` and resistivity of copper at room temperature is `1.7xx10^(-6)Omega cm`, find the relaxation time for the free electrons of copper. Given, mass of electron `=9.1xx10^(-31) kg` , and charge of electron `=1.6xx10^(-19)C`.
View SolutionWhat is the drift velocity for the electrons in a calculator when an electric field of strength `200 V//m` is applied on it and mobility of electrons is `4.5xx10^(-6) m^(2) V^(-1) s^(-1)`?
View SolutionA copper wire of length 2.0 m, of cross-sectional area 2.0 mm square carries a current of 0.4A. It is assumed that there is only one electron per atom. Atomic mass of copper is 63 g and density of copper is `8.9g//c`. Find the drift velocity for the electrons in the wire. Also find the mobility of electrons if a pot. difference of 100 V is applied across this wire.
View SolutionIf the current flowing through a copper wire of 1mm diameter is 1.1A. The density of copper is `9 g cm^(-3)` and atomic mass of copper is 63 u. One free electron is contributed by each atom of copper. Find the drift velocity of electron. Avogardo's number `=6.0 xx10^(26) ` per kg atom.
View SolutionFind the current flowing through a copper wire of length 0.2m, area of cross-section `1 mm^(2)`, when connected to a battery of 4 V. Given that electron mobility `=4.5xx10^(-6) m^(2)V^(-1) s^(-1)` and charge on electron `=1.6xx10^(-19)C`. The number density of electron in copper is `8.5 xx10^(28) m^(-3)`.
View Solution(a) Estimate the average drift speed of conduction electrons in a copper wire of cross sectional area `1.0xx10^(-7) m^2` carrying a current of 1.5 A. Assume that each copper atom contributes roughly one conduction electron. The density of copper is `9.0xx10^3 kgm^(-3)` and its atomic mass is `63.5 u.` (b) Compare the drift speed obtained with the speed of propagation of electric field along the conductor, which causes the drift motion.
View SolutionCalculate the resistivity of the material of a wire 1.0 m long, 0.4 mm diameter and having a resistance of `2.0 Omega`.
View SolutionA wire of resistance `5.0 Omega` is used to wind a coil of radius 5 cm. The wire has a diameter 2.0 mm and the specific resistance of its material is `2.0xx10^(-7)Omega m`. Find the number of turns in the coil.
View SolutionA wire of `10 Omega` resistance is stretched to thrice its original length. What will be its (i) new resistivity and (ii) new resistance?
View SolutionA wire has a resistance of `16 Omega`. It is melted and drawn into a wire of half its length. Calculate the resistance of new wire. What is the percentage change in its resistance?
View SolutionA piece of silver has a resistace of `2 Omega`. What will be the resistance of constantan wire of two-third length and one-third diameter, if the specific resistance of constantan is 30 times that of silver.
View SolutionThere are two wires A and B of same mass and of the same material. The diameter of wire A is one-third the diameter of wire B. If the resistance of wire A is `30 Omega`, find the resistance of wire B.
View SolutionIn a discharge tube the number of hydrogen ions (i.e., protons) drifting across a cross- section per second is `1.0xx10^(18)`, while number of electrons drifting in opposite direction across another cross-section is `2.5xx10^(18)` per second. If the supply voltage is 220 V, what is the effective resistance of the tube ?
View SolutionThe external diameter of a 4 m long hollow tube is 10 cm and thickness of its wall is 5 mm. If the specific resistance of the copper is `1.7xx10^(-8)Omega m`, then calculate its resistance.
View SolutionA potential difference of 3V is applied across a conductor of resistance `1.5 Omega`.
Calculate the number of electrons flowing through it in one second. Given charge on electron, `e=1.6 xx10^(-19)C`.
View SolutionFind the relaxation time for free electrons in copper, if the density of mobile electrons is `8.4 xx10^(28) m^(-3)`. The resistivity of copper at room temperature is `1.7xx10^(-8)Omega m`.
Given : mass of electron `=9.11 xx10^(-31) kg ` and charge on electron `=1.6xx10^(-19)C`.
View SolutionA wire of resistance `5Omega` is drawn out so that its length is increased by twice its original length. Calculate its new resistance.
View SolutionA copper wire is stretched to make it 0.2% longer. What is the percentage change in its resistance?
View SolutionWhen 5 V potential difference is applied across a wire of length 0.1 m. The drift speed of electrons is `2.5 xx 10^(-4) ms^(-1)`. If the electron density in the wire is `8 xx10^(28) m^(-3)`, calculate the resistivity of the material of wire
View SolutionFind the resistivity of a conductor in which a current density of 2.5 `A m^(-2)` is found to exist, when an electric field of `15 V m^(-1)` is applied on it.
View SolutionCalculate the electrical conductivity of the material of a conductor of length 3 m, area of cross- section `0.02 mm^(2)`, having a resistance of `2 Omega`.
View SolutionA wire carries a current of 0.5A, when a potential differnece of 1.5 V is applied across it. What is its conductance ? If the wire is of length 3 m and area of cross-section `5.4 mm^(2)`, calculate its conductivity.
View SolutionCalculate the electric field in a copper wire of cross-sectional area 2.0 mm square carrying a current of 2 A. The resistivity of copper is `1.7 xx 10^(-8)Omega m`.
View SolutionAn aluminium wire of diameter 2.5 mm is connectedf in series with a copper wire of diameter1.6 mm. A current of 2.0 A is passed through them. Find (a) current density in aluminium wire, (b) drift velocity of electrons in copper wire. Given the number density of conduction electrons in copper is `10^(29) m^(-3)`.
View SolutionCurrent flows through a constricted conductor as shown in figure
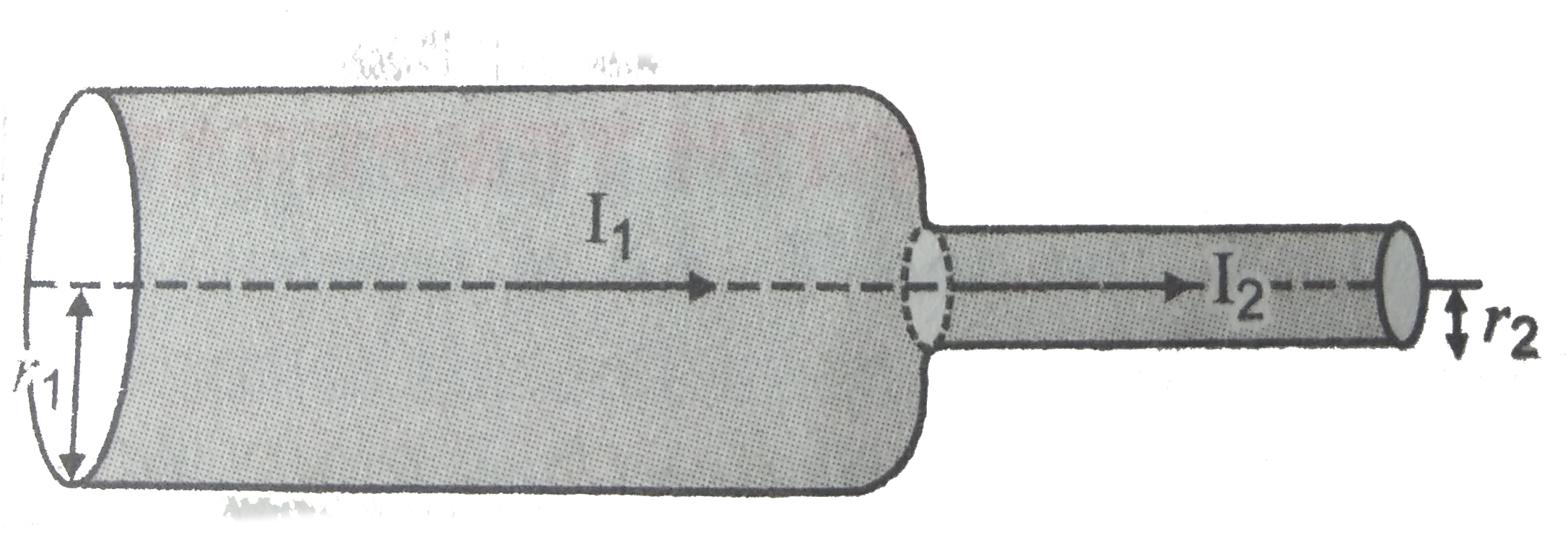
The radius and the current density to the left of constriction are 2 mm and `4.2xx10^(5)Am^(-2)`. (a) How much current flows through the constriction? (b) If the current density is doubled as emerges from the right side of the constriction, what is the radius `r_(2)`?
View SolutionCalculate the electric field in a copper wire of cross-sectional area 2.0 mm square carrying a current of 2 A. The resistivity of copper is `1.7 xx 10^(-8)Omega m`.
View SolutionThe number density of electron in copper is `8.5 xx10^(28)m^(-3)`. Find the current flowing through a copper wire of length 20 cm, area of cross section is 1 mm square,when connected to a battery of 3 V. Given the electron mobility `=4.5xx10^(-6)m^(2)V^(-1) s^(-1)` and electron charge `=1.6 xx 10^(-19)C`.
View SolutionAt what temperature(in kelvin) would the resistance of a copper wire be half its resistance at `0^@C`? Temperature coefficient of resistance of copper is `3.9 xx 10^(-3).^(@)C^(-1)`.
View SolutionA tungsten coil has a resistance `16 Omega` at `20^@C`. If the temperature coefficient of resistance of tungsten is `0.004^@C^(-1)`, calculate the resistance of the coil at `80^@C`.
View SolutionA conductor has a cross-section of `15 mm^(2)` and resistivity of `7.6 xx 10^(-8)Omega` m at `0^@C`. If the temperature coefficient of resistance of the material of the conductor is `5 xx 10^(-3).^(@)C^(-1)`, calculate its resistance for 2 km length of conductor when its temperature is `60^@C`.
View SolutionThe heating element of an electirc toaster is of nichrome. When a vary small current passes through it, at room temperrature `27^@C`, its resistance is `75.3Omega`. When toaster is connected to a 230V supply, the current settles after a few seconds to a steady value of 2.68A. What is the steady temperature of nichrome element? The temperature coefficient of resistance of nichrome over averged temperature range is `1.7xx10^(-4)^(@)C^(-1)`.
View SolutionThe resistance of a platinum wire of platinum resistance thermometer at the ice point is `5 Omega` and at steam point is `5.23 Omega`. When therometer is insertes in a hot bath, the resistance of the platinum wire is `5.795 Omega`. Calculate the temperature of the bath?
View SolutionA heating element using nichrome connected to a 115 V supply draws a current of 1.6A which settles after a few seconds to a steady value of 1.4 A. What is the steady temperature of the heating element if the room temperature is `30^@C` ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is `1.7xx10^(-4).^(@)C^(-1)`.
View SolutionA standard coil marked `5 Omega` is found to have a resistance of `5.128 Omega` at `30^@C`. Calculate the temperature at which the marking is correct. The temperature coefficient of resistance of the material of the coil is `.0042^@C^(-1)`.
View SolutionA potential difference of 120 V is applied to a coil at temperature of `12^@C` and the current is 6A. What will be the mean temperature of the coil when the curreny has fallen to 3 A, the applied voltage being the same as before ? Given temperature coefficient of resistance coil is `.00427^@C^(-1)` at `0^@C`.
View SolutionThe resistance of iron and copper wires at `20^@C` are `4.1Omega` and `4.3Omega` respectively. At what temperature will the resistance be equal ? Temperature coefficient of resistance for iron is `5.0xx10^(-3)K^(-1)` and for copper is `4.0xx10^(-3) K^(-1)`. Neglect any thermal expansion.
View SolutionResistivity of the material of a conductor of uniform cross-section varies along its length as `rho=rho_(0)(1+alpha x)`. Find its resistance if its length is L and area of cross-section is A.
View SolutionHow will you repersent a resistance of `3700 Omega +- 10%` by colour code?
View SolutionWhat is the colour of the third band of a coded resistor of resistance `2.3 xx 10^(2)Omega`?
View SolutionA current of 2 mA is passed through a colour coded carbon resistor with first, second and third rings of yellow, green and orange colours. What is the voltage drop across the resistor?
View SolutionA voltage of 5 V is applied across a colour coded carbon resistor. A current of 5 mA flows through it. What are the colours of second and third band of coded colour resistor?
View SolutionTwo coils have a combined resistance of `9 Omega` when connected in series and `2 Omega` when connected in parallel. Find the resistance of each coil.
View SolutionA resistor of `24 Omega` resistance is bent in the form of a circle as
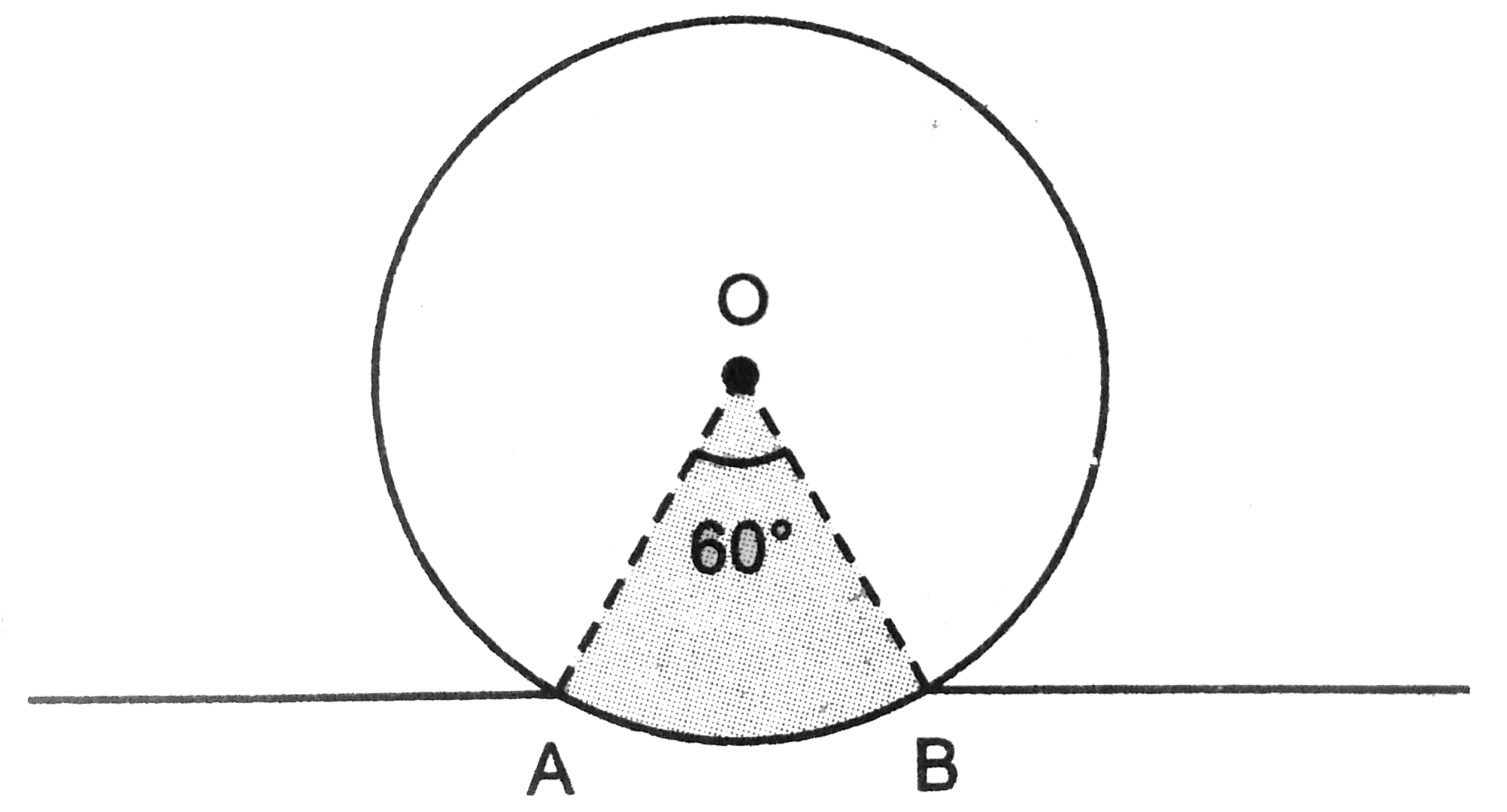 .
.
What is the effective resistance between points A and B?
View SolutionTwo resistance are in the ratio 1:4. if these are connected in parallel, their total resistance becomes 20 ohm. Find the value of each resistance
View SolutionTwo conductors of conductnaces `G_(1)` and `G_(2)` are connected in series. They are connected in parallel to another conductor of conductance `G_(3)`. Determine their equivalent conductance.
View SolutionTwo rods of copper and aluminium of each of equal length 20 cm and equal cross-sectional area `2 mm^(2)`. They are joined (i) in series and (ii) in parallel as shown in figure. Find the resistance of the combination in each case. Resistivity of copper `=1.7 xx10^(-8) Omega m` and resistivity of aluminium `= 2.6 xx 10^(-8)Omega m`.

View SolutionIn the given network of resistors, Find the equivalent resistance (i) between the points A and B (ii) between the points A and D (iii) between the points A and C.
View Solution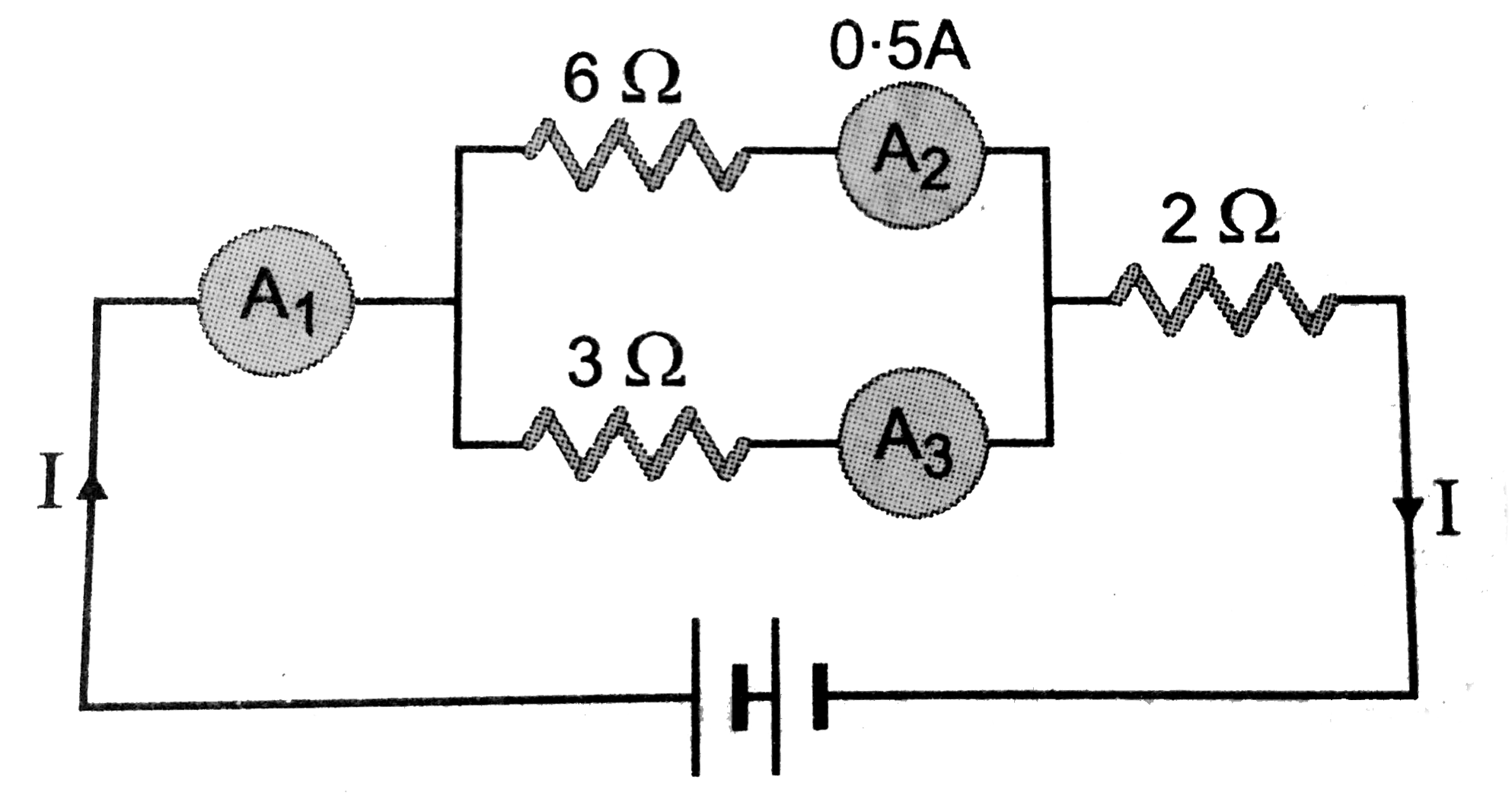
`A_(1), A_(2) and A_(3)` Are the ammeters and `A_(2)` reads 0.5A. (i) What are the readings of ammeters `A_(1)` and `A_(3)` ? (ii) What is the total resistance of the circuit ?
View SolutionThe resistance of two conductors in series is `40 Omega` and their resistance becomes `6.4 Omega`, when connected in parallel. Find the resistance of individual conductors.
View SolutionA resistor of `5 Omega` is connected in series with a parallel combination of a number of resistors each of `5 Omega`. If the total resistance of the combination is `6 Omega` , how many resistor are in parallel?
View SolutionA uniform wire of resistance R is shaped into a regular n sided polygon where n is even. Find the equivalent resistance between (i) opposite corners of polygon (ii) adjacent corners of polygon .
View SolutionA letter `A` is constructed as a uniform wire of resistance 1 ohm/cm. The sides of the letter are 20 cm long and the cross piece in the middle is 10 cm long while the vertex angle is `60^(@)` the resistance of the letter between the two ends of the legs is
View SolutionCalculate the potential difference between points B and D of the network of resistance shown in figure
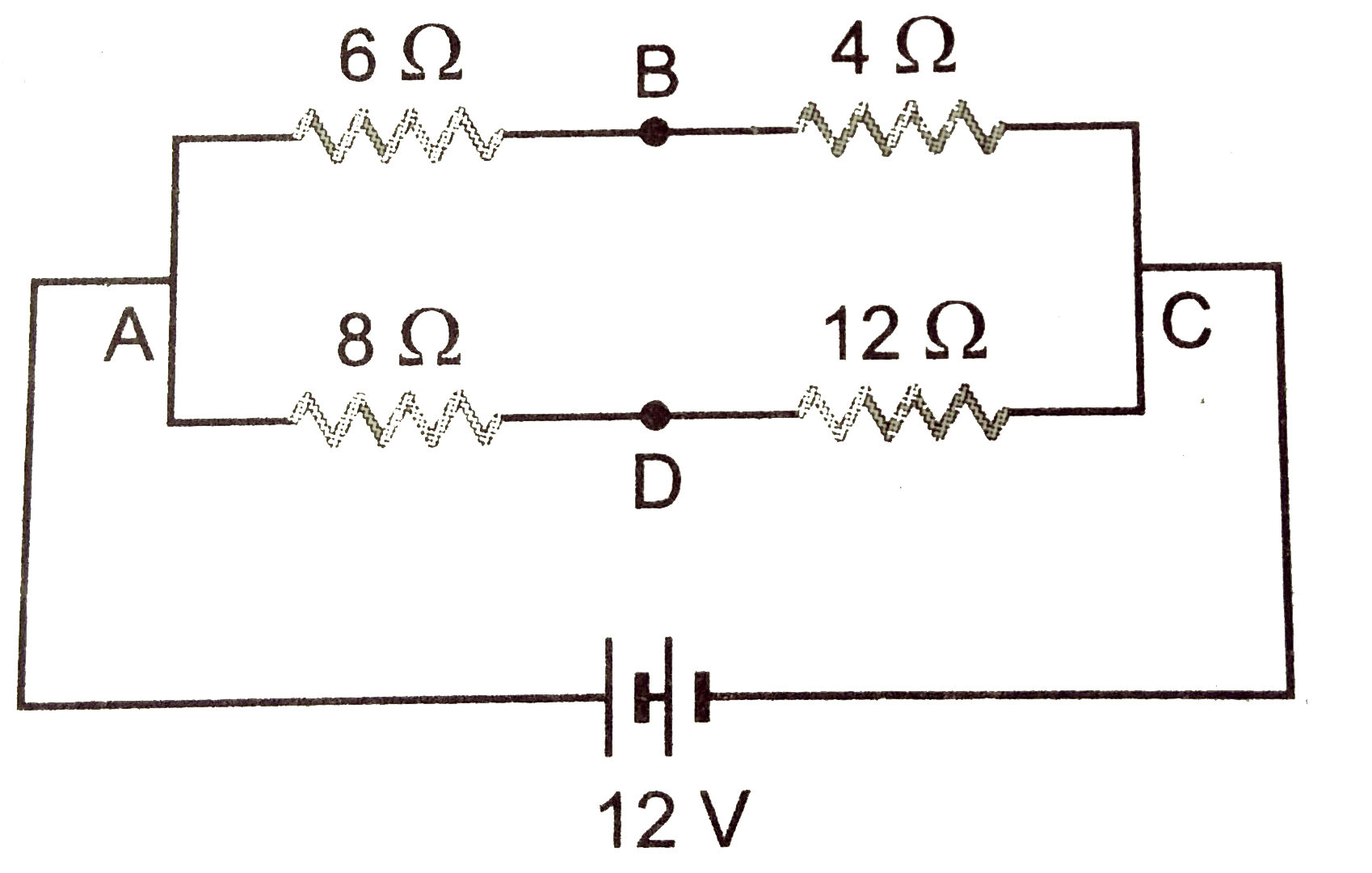
View SolutionIn the circuit shown in figure
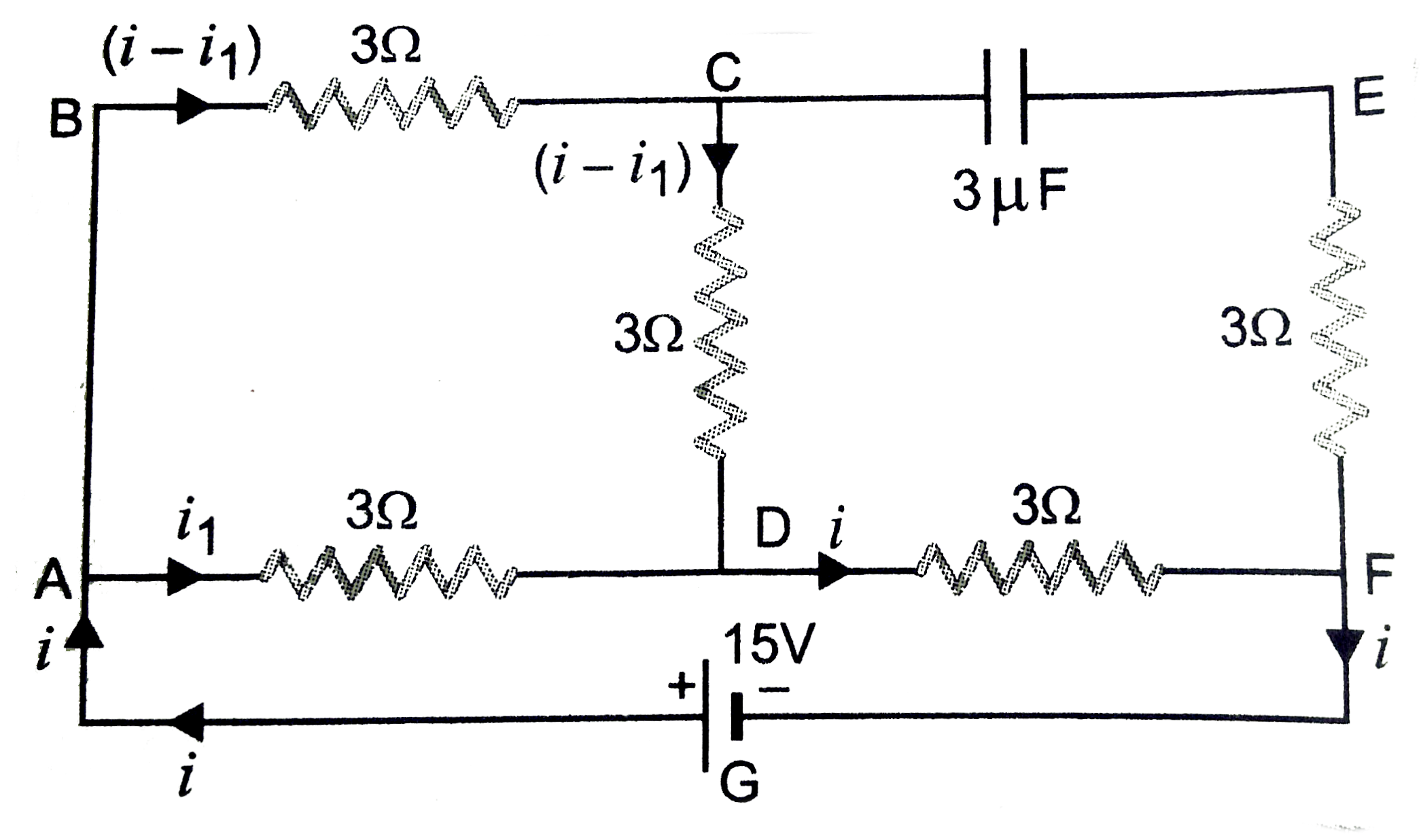
Find the potential differnece across capacitor.
View SolutionFour resistors of `12 Omega` each are connected in parallel . Three such combinations are then connected in series. What is the total resistance ? If a battery of 9 V emf and negligible internal resistance is connected across the networks, find the current flowing through of each resistors.
View SolutionSix equal resistances each of 4 ohm are connected to form a net work as shown in figure
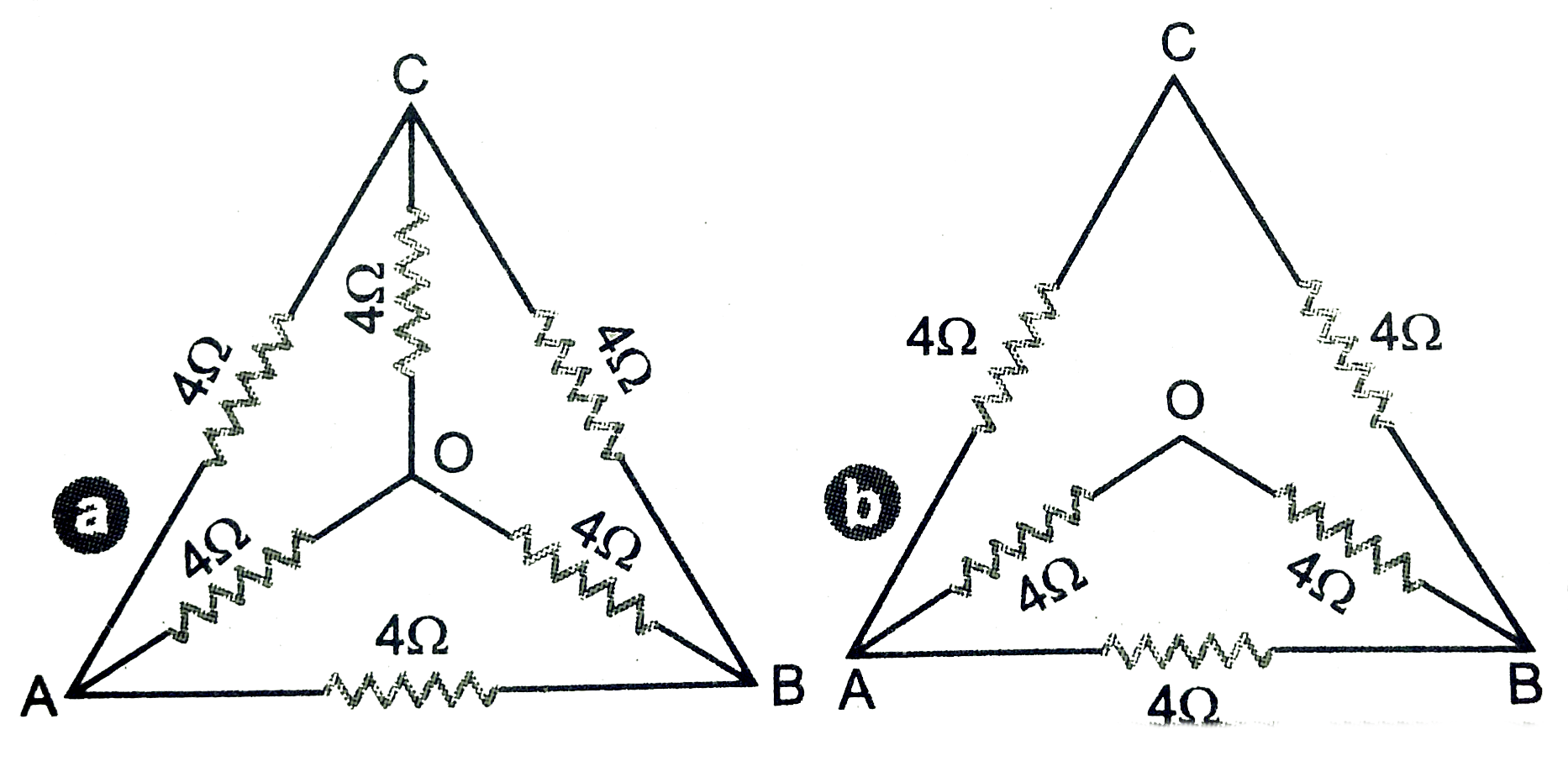 .
.
What is the resistance between A and B ?
View SolutionA resistor is connected to a battery of emf 10 V and internal resistance `0.3 Omega`. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA battery of emf 3V and internal resistance r is connected in series with a resistor of `55 Omega` through an ammeter of resistance `1 Omega`. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionThe cell has an emf of `2 V` and the internal resistance of this cell is `0.1 Omega`, it is connected to resistance of `3.9 Omega`, the voltage across the cell will be
View SolutionA cell of emf `epsilon` and internal resistance r gives a current of 0.5 A with an external resistance of `12 Omega` and a current of 0.25 A with an external resistance of `25 Omega`. Calculate (a) internal resistance of the cell and (b) emf of the cell.
View SolutionA uniform wire of resistance `12 Omega` is cut into three pieces in the ratio 1 : 2 : 3 and the three pieces are connected to form a triangle. A cell of emf 8 V and internal resistance `1 Omega` is connected across the highest of the three resistors. Calculate the current through each part of the circuit.
View SolutionThe emf of a battery is 6.0 V and its internal resistance is `1.5 Omega`. Its potential differences is measured by a voltmeter of resistance `1000 Omega`. Calculate the percentage error in the reading of emf shown by voltmeter.
View SolutionPotential differences across the terminals of a cell were measured (in volt) against different currents (in ampere) flowing through the cell. A graph was drawn which was a straight line ABC as shown in figure
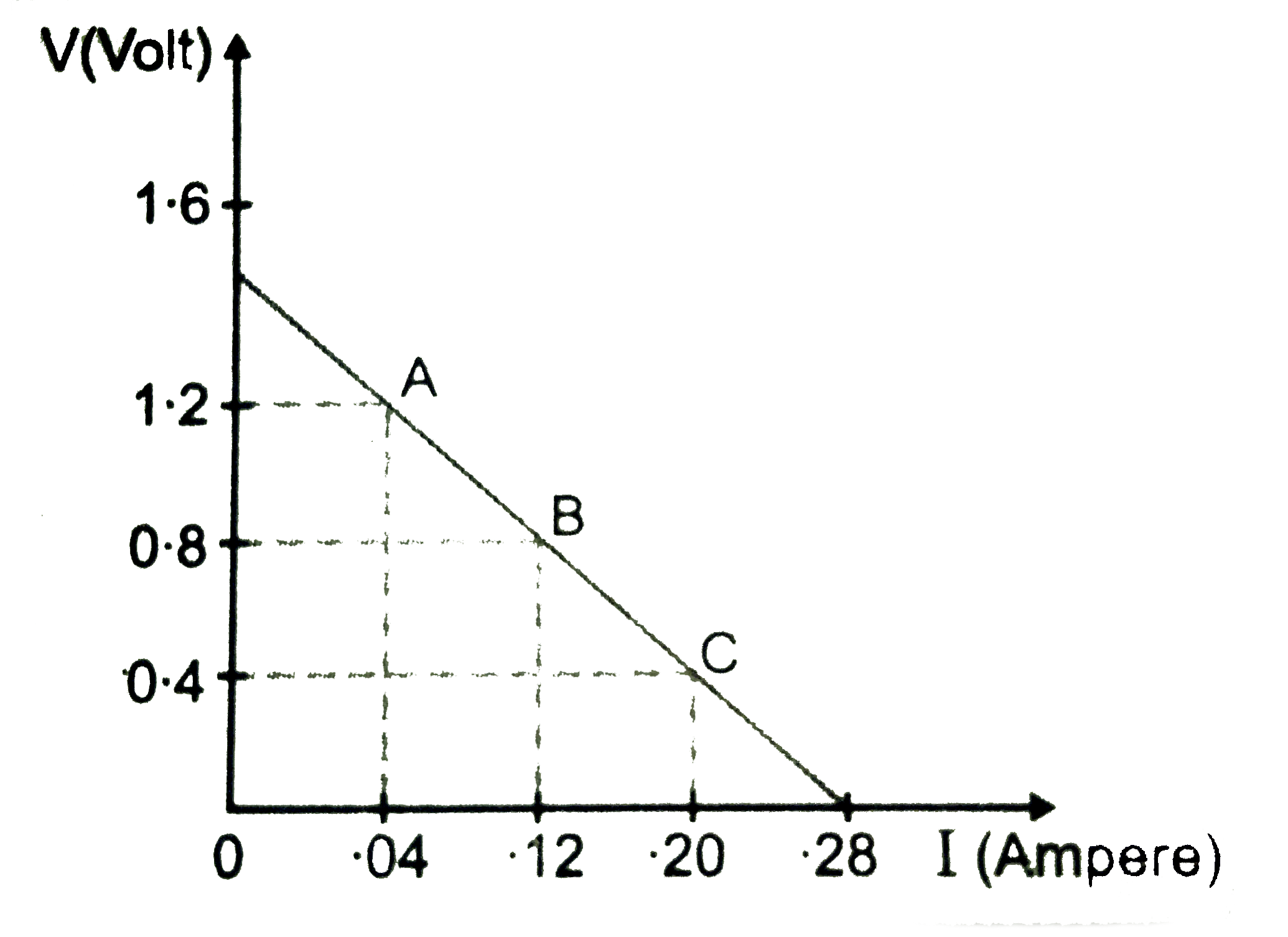
Determine from graph (i) emf of the cell (ii) maximum current obtained from the cell and (iii) internal resistance of the cell.
View SolutionFind the current drawn from a cell of emf 1 V and internal resistance `(2//3)Omega` connected to the network shown in figure

View SolutionTwo identical cells of emf 1.5 V each joined in parallel provided supply to an external circuit cosisting of two resistances of `17 Omega` each joined in parallel. A very high resistance voltmeter reads. The teminal voltage of cells to be 1.4V. Calculate the internal resistance of each cell.
View Solution
Solved Examples questions and complete solutions for chapter CURRENT ELECTRICITY of PRADEEP PHYSICS (HINGLISH) of Class 12