Complete Solutions to SAMPLE PROBLEM of chapter FORCE AND MOTION - I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FORCE AND MOTION - I |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Here are examples of how to use Newton's second law for a quck when one or two forces act on it. Parts (a), (b), and ( c ) of Fig. 5-3 show three situations in which one or two forces act on a puck that moves over frictionless ice along an x axis, in one-dimensional motion. The puck's mass is m = 0.20 kg. Forces `vec(F)_(1)` and `vec(F)_(2)` are directed along the axis and have magnitudes `F_(1)=4.0` N and `F_(2)=2.0` N. Force `vec(F)_(3)` is directed at angle `theta=30^(@)` and has magnitude `F_(3)=1.0` N. In each situation, what is the acceleration of the puck ?
View SolutionHere we find a missing force by using the acceleration. In the overhead view of Fig. 5-4a, a 2.0 kg cookie tin is accelerated at `3.0" m"//"s"^(2)` in the direction shown by `vec(a)`, over a frictionless horizontal surface. The acceleration is caused by three horizontal forces, only two of which are shown: `vec(F)_(1)` of magnitude 10 N and `vec(F)_(2)` of magnitude 20 N. What is the third force `vec(F)_(3)` in unit-vector notation and in magnitude-angle notation?
View SolutionA mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is `2.0xx10^(2)" N"//"m"`. Calculate the displacement x.
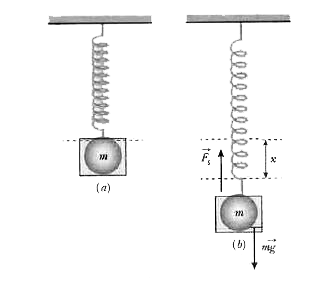
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
View SolutionA secret agent pushes two mysterious crates across a frozen river in the dark of night. The crates slide friction-lessly. Their masses are 150 kg (A) and 50 kg (B). The agent's hands exert a 100 N force on A (see Fig. 5-19). How much force does A exert on B? If there is no friction, can either block's acceleration be zero? Therefore, can `sum vec(F)_("on A")=0`? Therefore, can the force exerted on A by B (which is equal in magnitude to that exerted on B by A) "balance" (be equal and opposite to) the force exerted by the agent?

View SolutionFigure 5-20 shows a block S (the sliding block) with mass M = 3.3 kg. The block is free to move along a horizontal frictionless surface and connected, by a cord that wraps over a frictionless pulley, to a second block H (the hanging block), with mass m = 2.1 kg. The cord and pulley have negligible masses compared to the blocks (they are "massless"). The hanging block H falls as the sliding block S accelerates to the right. Find (a) the acceleration of block S, (b) the acceleration of block H, and ( c ) the tension in the cord.
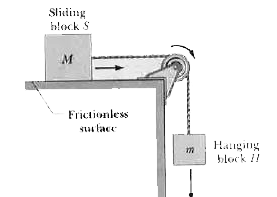
Figure 5.20 A block S of mass M is connected to a block H of mass m by a cord that wraps over a pulley.
View SolutionIn Fig. 5-23a, a cord pulls a box of sea biscuits up along a frictionless plane inclined at angle `theta=30.0^(@)`. The box has mass m = 5.00 kg, and the force from the cord has magnitude T = 25.0 N. What is the box's acceleration a along the inclined plane ?
View SolutionHere is an example of where you must dig information out of a graph, not just read off a number. In Fig. 5-24a, two forces are applied to a 4.00 kg block on a frictionless floor, but only force `vec(F)_(1)` is indicated. That force has a fixed magnitude but can be applied at an adjustable angle `theta` to the positive direction of the x axis. Force `F_(2)` is horizontal and fixed in both magnitude and angle. Figure 5-24b gives the horizontal acceleration `a_(x)` of the block for any given value of `theta` from `0^(@)` to `90^(@)`. What is the value of `a_(x)` for `theta=180^(@)` ?
View SolutionIn Fig. 5-25a, a passenger of mass m = 72.2 kg stands on a platform scale in an elevator cab. We are concerned with the scale readings when the cab is stationary and when it is moving up or down.
(a) Find a general solution for the scale readihng, whatever the vertical motion of the cab.
View SolutionWhat does the scale read if the cab is stationary or moving upward at a constant 0.50 m/s?
View SolutionIn Fig. 5-26a, a constant horizontal force `vec(F)_("app")` of magnitude 20 N is applied to block A of mass `m_(A)=4.0` kg, which pushes against block B of mass `m_(B)=6.0` kg. The blocks slide over a frictionless surface, along an x axis.
(a) What is the acceleration of the blocks ? `F_("app")=m_(A)alpha`.
However, this is seriously wrong because `vec(F)_("app")` is not the only horizontal force acting on block A. There is also the force `vec(F)_("AD")` from block B (Fig. 5-26b).
Dead-End Solution: Let us now include force `vec(F)_(AB)` by writing, again for the x axis,
`F_("app")-F_(AB)=m_(A)alpha`.
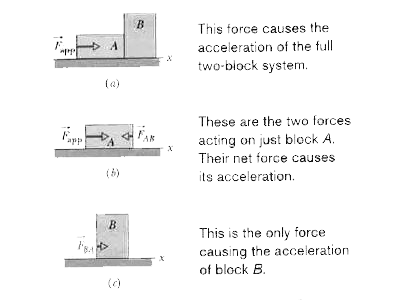
Figure 5-26 (a) A constant horizontal force `vec(F)_("app")` is applied to block A, which pushes against block B. (b) Two horizontal forces act on block A. (c) Only one horizontal force acts on block B.
(We use the minus sign to include the direction of `vec(F)_(AB)`.) Because `F_(AB)` is a second unkon, we cannot solve this equation for a.
Successful Solution: Because of the direction in which force `vec(F)_("app")` is applied, the two blocks form a rigidly connected system. We can relate the net force on the system to the acceleration of the system with Newton's second law. Here, once again for the x axis, we can write that law as
`F_("app")=(m_(A)+m_(B))alpha`,
where now we properly apply `vec(F)_("app")` to the system with total mass `m_(A)+m_(B)`. Solving for a and substituting known values, we find
`a=(F_("app"))/(m_(A)+m_(B))=(20" N")/)4.0" kg"+6.0" kg")=2.0" m"//"s"^(2)`.
Thus, the acceleration of the system and of each block is in the positive direction of the x axis and has the magnitude `2.0" m"//"s"^(2)`.
(b) What is the (horizontal) force `vec(F)_(BA)` on block B from block A (Fig. 5-26c) ?
View SolutionIn Fig. 5-27, a block attached to a chord is resting on an inclined plane. Let the mass of the block be 8.5 kg and the angle `theta` be `30^(@)`.
(a) Find the tension in the cord and normal force acting on the block.
(b) If the cord is cut, find the magnitude of the resulting acceleration of the block.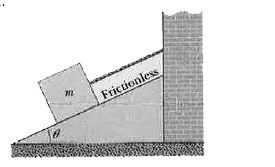
Figure 5-27 A block attached to a chord resting on an incline.
View SolutionIn Fig. 5-29, a block of mass m = 5.00 kg is pulled along a horizonttal frictionless floor by a cord that exerts a force of magnitude F = 12.0 at an angle `theta=25.0^(@)`.

Figure 5-29 A block is pulled along a horizontal floor.
(a) What is the magnitude of the block's acceleration?
View SolutionThe force magnitude F is slowly increased. What is its value just before the block is lifted (completely) off the floor ?

View SolutionIn Fig. 5-31, three ballot boxes are connected by cords, one of which wraps over a pulley having negligible friction on its axle and negligible mass. The three masses are `m_(A)=30.0` kg, `m_(B)=40.0` kg, and `m_(c)=10.0` kg.
(a) When the assembly is released from rest, what is the tension in the cord connecting B and C?
(b) When the assembly is released from rest, how far does A move in the first 0.250 s (assuming it does not reach the pulley)?

View SolutionA block of mass `m_(1)=3.70` kg on a frictionless plane inclined at angle `30.0^(@)` is connected by a cord over a massless, frictionless pulley to a second block of mass `m_(2)=2.30` kg (see Fig. 5-32).
(a) What is the magnitude of the acceleration of each block?
(b) What is the direction of the acceleration of the hanging block ?
(c) What is the tension in the cord?
View SolutionFigure 5-34 shows three blocks attached by cords that loop over frictionless pulleys. Block B lies on a friction-less table, the masses are `m_(A)=6.00` kg, `m_(B)=8.00` kg, and `m_(C)=10.0` kg. When the blocks are released, what is the tension in the cord at the right?
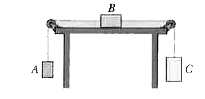
Figure 5-34 Three blocks attached over two pulleys by a cord.
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m, as shown in Fig. 5-35. A horizontal force acts on one end of the rope.

(a) Show that the rope must sag, even if only by an imperceptible amount.
(b) Then, assuming that the sag is negligible, find the acceleration of rope and block.
(c) Find the force on the block from the rope.
(d) Find the tension in the rope at its midpoint.
View SolutionA customer sits in an amusement park ride in which the compartment is to be pulled downward in the negative direction of a y axis with an acceleration magnitude of 1.24 g, with `g=9.80" m"//"s"^(2)`. A 0.567 g coin rests on the customer's knee. Once the motion begins and in unit-vector notation,
(a) What is the coin's acceleration relative to the ground?
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter FORCE AND MOTION - I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12