Complete Solutions to PROBLEMS of chapter FORCE AND MOTION - I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FORCE AND MOTION - I |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
When two perpendicular forces 9.0 N (toward positive x) and 7.0 N (toward positive y) act on a body of mass 6.0 kg, what are the (a) magnitude and (b) direction of the acceleration of the body ?
View SolutionTwo horizontal forces act on a 2.5 kg chopping block that can slide over a frictionless kitchen counter, which lies in an xy plane. One force is `vec(F)_(1)=(3.0" N")hati+(4.0N)hatj`. Find the acceleration of the chopping block in unit-vector notation when the other force is (a) `vec(F)_(2)=(-3.0N)hati+(-4.0N)hatj`, (b) `vec(F)_(2)=(-3.0N)hati+(4.0N)hatj`, and (c) `vec(F)_(2)=(3.0N)hati+(-4.0N)hatj`.
View SolutionA body has an acceleration of `3.00" m"//"s"^(2)` at `30.0^(@)` to the positive direction of an x axis. The mass of the body is 2.00 kg. Find (a) the x component and (b) the y component of the net force acting on the body. ( c ) What is the net force in unit-vector notation ?
View SolutionA particle is to move along a line at the constant velocity `vec(v)=(2m//s)hati-(3m//s)hatj`. During the motion of the particle, we assume that two forces are acting on it. If one of the forces is `vec(F)=(2N)hati+(-5N)hatj`, find the other force.
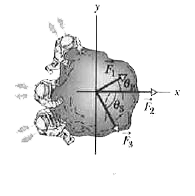
View SolutionThree astronauts, propelled by jet backpacks, push and guide a 120 kg asteroid toward a processing dock, exerting the forces shown in Fig. 5-37, with `F_(1)=32N,F_(2)=55N,F_(3)=41N, theta_(1)=30^(@)`, and `theta_(3)=60^(@)`. What is the asteroid's acceleration (a) in unit-vector notation and as (b) a magnitude and (c) a direction relation relative to the positive direction of the x axis ?
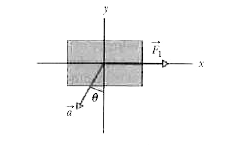
View SolutionThere are two forces on the 2.00 kg box in the overhead view of Fig. 5-38, but only one is shown. For `F_(1)=20.0N,a=12.0" m"//"s"^(2)`, and `theta=30.0^(@)`, find the second force (a) in unit-vector notation and as (b) a magnitude and ( c ) an angle relative to the positive direction of the x axis.
View SolutionA 1.50kg object is subjected to three forces that give it an acceleration `vec(a)=-(8.00"m"//"s"^(2))hatj`. If two of the three forces are `vec(F)_(1)=(30.0N)hati+(16.0N)hatj` and `vec(F_(2))=-(12.0N)hati+(8.00N)hatj`, find the third force.
View SolutionIn an xy plane, a 0.450 kg object moves is such a way that `x(t)=-16.0+3.00t-5.00t^(3)` and `y(t)=26.0+8.00t-10.0t^(2)`, where x and y are measured in meters and t in seconds. At t = 0.800 s, find (a) the magnitude and (b) the angle, relative to the positive direction of the x axis, of the net force on the object, and ( c ) the angle of the object's travel direction.
View SolutionA 0.150 kg particle moves along an x axis according to `x(t)=-13.00+2.00t+4.00t^(2)-3.00t^(3)`, with x in meters and t in seconds. In unit-vector notation, what is the net force acting on the particle at `t=2.60" s"` ?
View SolutionA 3.0 kg object is driven along an x axis by a variable force that is directed along that axis. Its position is given by `x=4.0" m"+(5.0" m"//"s")t+kt^(2)-(3.0" m"//"s"^(3))t^(3)`, where x is measured in meters and t in seconds. The factor k is a constant. At t = 4.0 s, the force on the particle has a magnitude of 37 N and is in the negative direction of the axis. Find the value of k.
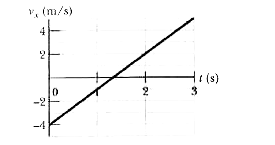
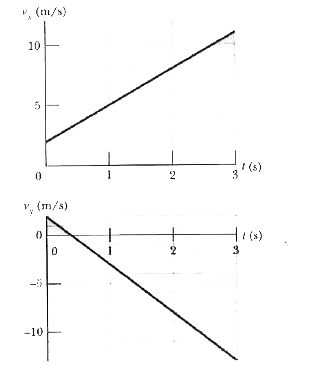
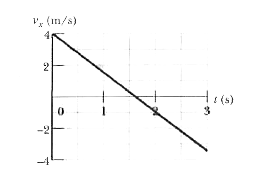
View SolutionTwo horizontal forces `vec(F)_(1)` and `vec(F)_(2)` act on a 4.0 kg disk that slides over frictionless ice, on which an xy coordinate system over frictionless ice, on which an xy coordinate system is laid out. Force `vec(F)_(1)` is in the positive direction of the x axis and has a magnitude of 7.0 N. Force `vec(F)_(2)` has a magnitude of 9.0 N. Figure 5-39 gives the x component `v_(x)` of the velocity of the disk as a function of time t during the sliding. What is the angle between the constant directions of forces `vec(F)_(1)` and `vec(F)_(2)` ?
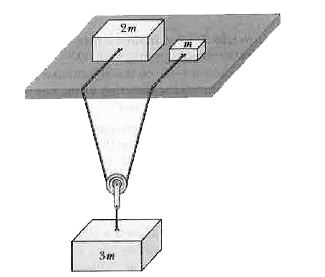
View SolutionTwo particles of masses m and 2m are placed on a smooth horizonttal table. A string, which joins these two masses, hangs over the edge supporting a pulley, which suspends a particle of mass 3m, as shown in Fig. 5-40. The pulley has negligible mass. The two parts of the string on the table are parallel and perpendicular to the edge of the table. The hanging parts of the string are vertical. Find the acceleration of the particle of mass 3m.
View SolutionA block with a weight of 4.0 N is at rest on a horizontal surface A 1.0 N upward force is applied to the block by means of an attached vertical string. What are the (a) magnitude and (b) direction of the force of the block on the horizontal surface ?
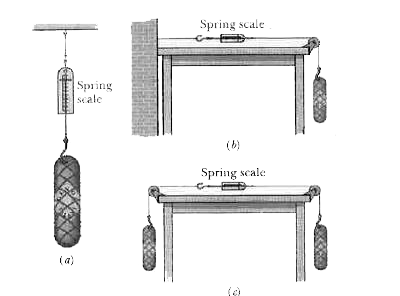
View Solution(a) An 11.0 kg salami is supported by a cord that runs to a spring scale, which is supported by a cord hung from the ceiling (Fig. 5-41a). What is the reading on the scale, which is marked in SI weight units? (This is a way to measure weight by a cord that runs around a pulley and to a scale.The opposite end of the scale? (This is the way by a physics major.) ( c ) In Fig. 5-41c the wall has been replaced with a second 11.0 kg salami, and the assembly is stationary. What is the reading on the scale? (This is the way by a deli owner who was once a physics major.)
View SolutionA 550 kg rocket sled can be accelerated at a constant rate from rest to 1650 km/h in 2.0 s. What is the magnitude of the required net force ?
View SolutionA car traveling at 63 km/h hits a bridge abutment. A passenger in the car moves forward a distance of 65 cm (with respect to the road) while being brought to rest by an inflated air bag. What magnitude of force (assumed constant) acts on the passenger's upper torso, which has a mass of 41 kg ?
View SolutionA constant horizontal force `vec(F)_(a)` pushes a 2.00 kg package across a frictionless floor on which an xy coordinate system has been drawn. Figure 5-42 gives the package's x and y velocity components versus time t. What are the (a) magnitude and (b) direction of `vec(F)_(a` ?
View SolutionTarzan, who weighs 860 N, swings from a cliff att the end of a 20.0 m vine that hangs from a high tree limb and initially makes an angle of `22.0^(@)` with the vertical. Assume that an x axis extends horizontally away from the cliff edge and a y axis extends upward. Immediately after Tarzan steps of the cliff, the tension in the vine is 760 N. Just then, what are (a) the force on him from the vine in unit-vector notation and as (c) a magnitude and (d)an angle relative to the positive direction of Tarzon's acceleration just then ?
View SolutionThere are two horizontal forces on the 2.0 kg box in the overhead view of Fig. 5-43 but only one (of magnitude `F_(1)=30" N"`) is shown. The box moves along the x axis. For each of the following values of the acceleration `a_(x)` of the box, find the second force in unitvector notation: (a) `10" m"//"s"^(2)`, (b) `20" m"//"s"^(2)`, (c) 0, (d) `-10" m"//"s"^(2)`, and (e) `-20" m"//"s"^(2)`.

View SolutionThe tension at which a fishing line snaps is commonly called the line's "strength." What minimum strength is needed for a line that is to stop a salmon of weight 90 N in 11 cm if the fish is initially drifting at 2.8 m/s ? Assume a constant deceleration.
View SolutionA car that weighs `1.30xx10^(4)` N is initially moving at 35 km/h when the brakes are applied and the car is brought to a stop in 15 m. Assuming the force that stops the car is constant, find (a) the magnitude of the force and (b) the time required for the car experiences the same force during the braking, by what factors are (c) the stopping distance and (d) the stopping time multiplied? (There could be a lesson here about the danger of driving at high speeds.)
View SolutionA firefighter who weighs 689 N slides down a vertical pole with an acceleration of `2.00" m"//"s"^(2)`, directed downward. What are the (a) magnitude and (b) direction (up or down) of the vertical force on the firefighter from the pole and the ( c ) magnitude and (d) direction of the vertical force on the pole from the firefighter ?
View SolutionFigure 5-44 shows an overhead view of a 0.0250 kg lemon half and two of the three horizontal forces that act on it as it is on a fric tionless table. Force `vec(F)_(1)` has a magnitude of 6.00 N and is at `theta_(1)=30.0^(@)`. Force `vec(F)_(2)` has a magnitude of 7.00 N and is at
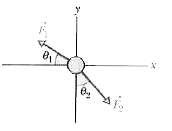
`theta_(2)=30.0^(@)`. In unit-vector notation, what is the third force if the lemon half (a) is stationary, (b) has the constant velocity `vec(v)=(13.0hati-14.0hatj)` m/s, and ( c ) has the varying velocity `bar(v)=(13.0t hati-14.0t hatj)" m"//"s"^(2)`, where t is time?
View SolutionA 1500 kg cable car moves vertically by means of a cable that connects the ground and the top of a hill. What is the tension in the supporting cable when the cab, originally moving downard at a speed of 9.0 m/s, is brought to rest with constant acceleration in a distance of 38 m.
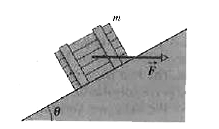
View SolutionIn Fig. 5-45, a crate of mass m = 115 kg is pushed at constant speed up a frictionless ramp `(theta=30.0^(@))` by a horizontal force `vec(F)`. What are the magnitudes of (a) `vec(F)` and (b) the force on the crate from the ramp ?
View SolutionAn object weighs 2.50 kg. In time t, measured in seconds, the velocity of the object is given by `bar(v)=(7.00t hati+2.00t^(2)hatj)` m/s. At the instant the net force on the object has a magnitude of 35.0 N, what are the direction of the net force and the object's direction of travel ?
View SolutionHolding on to a tow rope moving parallel to a frictionless ski slope, a 45 kg skier is pulled up the slope, which is at an angle of `8.0^(@)` with the horizontal. What is the magnitude `F_("rope")` of the force on the skier from the rope when (a) the magnitude v of the skier's velocity is constant at 2.0 m/s and (b) v = 2.0 m/s as v increases at a rate of `0.10" m"//"s"^(2)` ?
View SolutionA boy with a mass of 35 kg and a sled with a mass of 6.5 kg are on the frictionless ice of a frozen lake, 12 m apart but connected by a rope of negligible mass. The boy exerts a horizontal 4.2 N force on the rope. What are the acceleration magnitudes of (a) the sled and (b) the boy ? ( c ) How far from the boy's initial position do they meet ?
View SolutionA 50 kg skier skis directly down a frictionless slope angled at `10^(@)` to the horizontal. Assume the skier moves in the negative direction of an x axis along the slope. A wind force with component `F_(x)` acts on the skier. What is `F_(x)` if the magnitude of the skier's velocity is (a) constant, (b) increasing at a rate of `1.0" m"//"s"^(2)`, and (c) increasing at a rate of `2.0" m"//"s"^(2)` ?
View SolutionA bead of mass `2.5xx10^(-4)` kg is suspended from a cord. A steady horizontal breeze pushes the bead so that the cord makes a constant angle of `40^(@)` with the vertical. Find (a) the tension in the cord and (b) the push magnitude.
View SolutionA dated box of dates, of mass 4.50 kg, is sent sliding up a frictionless ramp at an angle of `theta` to the horizontal. Figure 5-46 gives, as a function of time t, the component `v_(x)` of the box's velocity along an x axis that extends directly up the ramp. What is the magnitude of the normal force on the box from the ramp ?
View SolutionIn earlier days, horses pulled barges down canals in the manner shown in Fig. 5-47. Suppose the horse pulls on the rope with a force of 8600 N at an angle of `theta=18^(@)` to the direction of motion of the barge, which is headed straight along the positive direction of an x axis. The mass of the barge is 9500 kg, and the magnitude of its acceleration is `0.12" m"//"s"^(2)`. What are the (a) magnitude and (b) direction (relative to positive x) of the force on the barge from the water ?

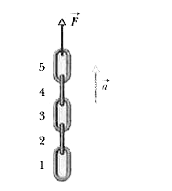
View SolutionIf Fig. 5-48, a chain consisting of five links, each of mass 0.100 kg, is lifted vertically with constant acceleration of magnitude `a=2.50" m"//"s"^(2)`. Find the magnitudes of (a) the force on link 1 from link 2, (b) the force on link 2 from link 3, (c) the force on link 3 from link 4, and (d) the force on link 4 from link 5. Then find the magnitudes of (e) the force `vec(F)` on the top link from the person lifting the chain and (f) the net force accelerating each link.
View SolutionA lamp hangs vertically from a cord in a descending elevator that decelerates at `2.4" m"//"s"^(2)`. (a) If the tension in the cord is 93 N, what is the lamp's mass? (b) What is the cord's tension when the elevator ascends with an upward acceleration of `2.4" m"//"s"^(2)` ?
View SolutionAn elevator cab that weighs 29.0 kN moves upward. What is the tension in the cable if the cab's speed is (a)increasing at a rate of `1.50" m"//"s"^(2)` and (b) decreasing at a rate of `1.50" m"//"s"^(2)` ?
View SolutionAn elevator cab is pulled upward by a cable. The cab and its single occupant have a combined mass of 2000 kg. When that occupant drops a coin, its acceleration relative to the cab is `8.30" m"//"s"^(2)` downward. What is the tension in the cable?
View SolutionThe Zacchini family was renowned for their human-cannonball act in which a family member was shot from a cannon using either elastic bands or compressed air. In one version of the act, Emanuel Zacchhini was shot over three Ferris wheels to land in a net at the same height as the open end of the cannon and at a range of 69 m. He was propelled inside the barrel for 5.2 m and launched at an angle of `53^(@)`. If his mass was 85 kg and he underwent consttant acceleration inside the barrel, what was the magnitude of the force propelling him? (Hint: Treat the launch as though it were along a ramp at `53^(@)`. Neglect air drag.)
View SolutionFigure 5-50 shows two blocks connected by a cord (of negligible mass) that passes over a frictionless pulley (also of negligible mass). The arrangement is known as Atwood's machine. One block has mass `m_(1)=1.30` kg, the other has mass `m_(2)=2.80` kg. What are (a) the magnitude of the blocks' acceleration and (b) the tension in the cord ?
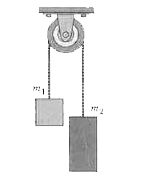
View SolutionA 93 kg man lowers himself to the grouund from a height of 10.0 m by holding onto a rope that runs over a frictionless pulley to a 65 kg sandbag. With runs over a frictionless pylley to a 65 kg sandbag. With what speed does the man hit the ground if he started from rest ?
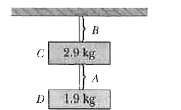
View SolutionAs shown in Fig. 5-51, body C (2.9 kg) and body D (1.9 kg) are suspended from a rigid support by inextensible wires B and A, each of length 1.0 m. Wire B has negligible mass, wire A has a uniform density of 0.20 kg/m. The whole system undergoes an upward acceleration of magnitude `0.50" m"//"s"^(2)`. Find the tension at the midpoint in (a) wire A and (b) wire B.
View SolutionFigure 5-52 shows four penguins that are being play-fully pulled along very slippery (frictionless) ice by a curator. The masses of three penguins and the tension in two of the cords are `m_(1)=12" kg",m_(3)=15" kg",m_(4)=20` kg, `T_(2)=111` N, and `T_(4)=222` N. Find the penguin mass `m_(2)` that is not given.

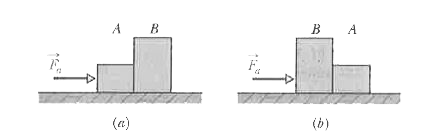
View SolutionTwo blocks are in contact on a frictionless table. A horizontal force is applied to the larger block, as shown in Fig. 5-53. (a) If `m_(1)=2.3" kg", m_(2)=1.2" kg",` and F = 3.2 N, find the magnitude of the force between the two blocks. (b) Show that if a force of the same magnitude F is applied to the smaller block but in the opposite direction, the magnitude of the force between the blocks is 2.1 N, which is not the same value calculated in (a). (c) Explain the difference.

View SolutionIn Fig. 5-54a, a constant horizontal force `vec(F)_(a)` is applied to block A, which pushes against block B with a 15.0 N force directed horizontally to the right. In Fig. 5-54b, the same force `vec(F)_(a)` is applied to block B, now block A pushes on block B with a 10.0 N force directed horizontally to the left. The blocks have a combined mass of 12.0 kg. What are the magnitudes of (a) their acceleration in Fig. 5-54a and (b) force `vec(F)_(a)` ?
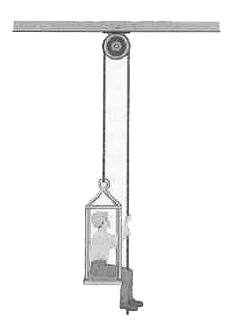
View SolutionFigure 5-55 shows a man sitting in a bosun's chair that dangles from a mass-less rope, which runs over a massless, frictionless pulley and back down to the man's hand. The combined mass of man and chair is 103.0 kg. With what force magnitude must the man pull on the rope if he is to rise (a) with a constant velocity and (b) with an upward acceleration of `1.30" m"//"s"^(2)` ?
View SolutionA 10 kg monkey climbs up a massless rope that runs over a frictionless tree limb and back down to a 15 kg package on the ground (Fig. 5-56). (a) What is the magnitude of the least acceleration the monkey must have if it is to lift the package off the ground? If, after the package has been lifted, the monkey stops its climb and holds on to the rope, what are the (b) magnitude and (c) direction of the monkey's acceleratiohn and (d) the tension in the rope ?

View SolutionFigure shows a 5.00 kg block being pulled along a frictionless floor by a cord that applies a force of constant magnitude 15.0 N but with an angle `theta(t)`that varies with time. When angle `theta=25.0^(@)`, at what rate is the acceleration of the block changing if (a) `theta(t)=(2.00xx10^(-2) deg//s)t` and (b) `theta(t)=-(2.00xx10^(-2) deg//s)t` ?

View SolutionA hot-air balloon of mass M is descending vertically with downward acceleration of magnitude a. How much mass (ballast) must be thrown out to give the balloon an upward acceleration of magnitude a? Assume that the upward force from the air (the lift) does not change because of the decrease in mass.
View SolutionIn shot putting, many athletes elect to launch the shot at an angle that is smaller than the theoretical one (about `42^(@)`) at which the distance of a projected ball at the same speed and height is greatest. One reason has to do with the speed the athlete can give the shot during the acceleration phase of the throw. Assume that a 7.260 kg shot is acclerated along a straight path of length 1.650 m by a constant applied force of magnitude 380.0 N, starting with an initial speed of 2.500 m/s (due to the athlete's preliminary motion). What is the shot's speed at the end of the acceleration phase if the angle between the path and the horizontal is (a) `30.00^(@)` and (b) `42.00^(@)` ?
(c) By what percentage is the launch speed decreased if the athlete increases the angle from `30.00^(@)` to `42.00^(@)` ?
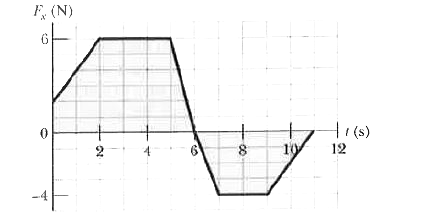
View SolutionFigure 5-58 gives, as a function of time l, the force component F, that acts on a 3.00 kg ice block is moving in the positive direction of the axis, with a speed of 3.0 m/s. What are its speed and (b) direction of travel of travel at t = 11 s ?
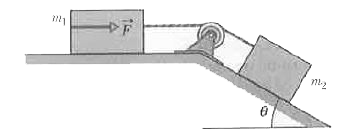
View SolutionFigure 5-59 shows a box of mass `m_(2)=1.0` kg on a friction-less plane inclined at angle `theta=30^(@)`. It is connected by a cord of negligible mass to a mass `m_(1)=2.5` kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force `vec(F)` is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of `vec(F)` may have without the cord becoming slack?
View SolutionFigure 5-50 shows Atwood's machine, in which two containers are connected by a cord (of negligible mass) passing over a frictionless pulley (also of negligible mass). At time t = 0, container 1 has mass 1.30 kg and container 2 has mass 2.80 kg, but container 1 is losing mass (through a leak) at the constant rate of 0.200 kg/s. At what rate is the acceleration magnitude of the containers changing at (a) t = 0 and (b) t = 3.00 s? (c) When does the acceleration reach its maximum value ?
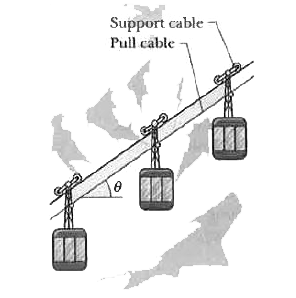
View SolutionFigure 5-60 shows a section of a cable-car system. The maximum permissible mass of each car with occupants is 2750 kg. The cars, riding on a support cable, are pulled by a second cable attached to the support tower on each car. Assume that the cables are taut and inclined at angle `theta=35^(@)`. What is the difference in tension between adjacent sections of pull cable if the cars are at the maximum permissible mass and are being accelerated up the incline at `0.81" m"//"s"^(2)` ?
View Solution
PROBLEMS questions and complete solutions for chapter FORCE AND MOTION - I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12