Complete Solutions to PROBLEMS of chapter WORK, POWER, AND ENERGY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WORK, POWER, AND ENERGY |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
When accelerated along a straight line at `2.8xx10^(15)m//s^(2)` in a machine, an electron ( mass `m=9.1xx10^(-31)kg`) has an initial speed of `1.4xx10^(7)` m/s and travels 5.8 cm. Find (a) the final speed of the electron and (b) the increase in its kinetic energy.
View SolutionIf a Saturn V rocket with an Apollo spacecraft attached had a combined mass of `2.9xx10^(5)` kg and reached a speed of 11.2 m/s, how much kinetic energy would it then have ?
View SolutionA father racing his son has half the kinetic energy of the son, who has half the mass of the father. The father speeds up by 1.0 m/s and then has the same kinetic energy as the son. What are the original speeds of (a) the father and (b) the son ?
View SolutionA ice block floating in a river is pushed through a displacement `vec(d)=(20m) hat(i) - (16 m) hat(j)` along a straight embankment by rushing water, which exerts a force `vec(F)= (210 N) hat(i)-(150 N) hat(j)` on the block. How much work does the force do on the block during the displacement ?
View SolutionThe only force acting on a 2.0kg canister that is moving in an xy plane has a magnitude of 5.0 N. The canister initially has a velocity of 4.0 m/s in the positive `x` direction and some time later has a velocity of 6.0 m/s in the positive y direction . How much work is done on the canister by the 5.0 N force during this time ?
View SolutionA coin slides over a frictionless plane and across an xy coordinate system from the origin to a point with xy coordinates ( 3.0 m , 4.0 m) while a constant force acts on it. The force has magnitude 2.5 N and is directed at a counter-clockwise angle of `100^(@)` from the positive direction of the x axis. How much work is done by the force on the coin during the displacement ?
View SolutionA particle travels through a three-dimensional displacement given by `vec(d)=(5.00 hat(i) - 3.00 hat(j) + 4.00 hat(k))m`. If a force of magnitude 22.0 N and with fixed orientation does work on the particle, find the angle between the force and the displacement if the change in the particle's kinetic energy is (a) 45.0 J and (b) -45.0 J.
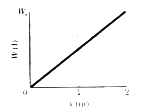
View SolutionA can of bolts and nuts is pushed 2.00 m along an x axis by a broom along the greasy ( frictionless ) floor of car repair shop in a version of shuffleboard. Figure 8-46 gives the work W done on the can by the constant horizontal force from the broom, versus the can's position `x`. The scale of the figure's vertical axis is set by `W_(s)=6.0J`. (a) What is the magnitude of that force ? (b) If the can had an initial kinetic energy of 3.00 J, moving in the positive direction of the `x` axis, what is its kinetic energy at the end of the 2.00 m ?
View SolutionA sledge and its rider, with a total mass of 85 kg, emerge fro a downhill track onto a horizontal straight track with an initial speed of 37 m/s. If a force slows them to a stop at a constant rate of `2.0 m//s^(2)`, (a) what magnitude F is required for the force, and (c) what work W is done on them by the force ? What work W is done on them by the force ? What are (d) F, (e) d, and (f) W if they, instead, slow at `4.0 m//s^(2)` ?
View SolutionA military helicopter lifts a 75 kg flood survivor 16 m vertically from the river by a rope. If the acceleration of the survivor is g/10, how much work is done on the survivor by (a) the force from the helicopter and (b) the gravitational force on her ? Just before she reaches the helicopter, what are her (c) kinetic energy and (d) speed ?
View SolutionA cord is used to vertically lower an initially stationary block of mass M at a constant downward acceleration of g/4. When the block has fallen a distance d, find (a) the work done by the cord's force on the block, (b) the work done by the graviational force on the block, (c) the kinitic energy of the block, and (d) the speed of the block.
View SolutionA cave rescue team lifts an injured person directly upward and out of a sinkhole by means of a motor-driven cable. The lift is performed in three stages, each requiring a vertical distance of 12.0 m: (a) the initially stationary spelunker is accelerated to a speed of 5.00 m/s, (b) he is then lifted at the constant speed of 5.00 m/s, (c) finally he is decelerated to zero speed. How much work is done on the 85.0 kg rescuee by the force lifting him during each stage ?
View SolutionA spring of spring constant `5 xx 10^(2) `Nm is streched initially by `5 cm` from the unstriched position . Then the work required to streach is further by another `5 cm` is
View SolutionA spring and block are in the arrangement of Fig. 8-12. When the block is pulled out to `x= +4.0 cm`, we must apply a force of magnitude 360 N to hold it there. We pull the block to `x=11` cm and then release it. How much work does the spring do on the block as the block moves from `x_(i)= +5.0cm` to (a) `x= +3.0 cm`, (b) `x = 3.0 cm`, (c) `x= -5.0 cm`, and (d) `x = -9.0 cm` ?
View SolutionAs a 2.5 kg body moves in the positive direction along an `x` axis, a single force acts on it. The force is given by `F_(x)= -6x N`, with `x` in meters. The velocity at `x=3.5m` is 8.5 m/s. (a) Find the velocity of the body at `x=4.5` m. (b) Find the positive value of `x` at which the body has a velocity of 5.5 m/s.
View SolutionThe block in Fig. 8-12a lies on a horizontal frictionless surface, and the spring constant is 50 N/m. Initially, the spring is at its relaxed length and the block is stationary at position `x=0`. Then an applied force with a constant magnitude of 3.0 N pulls the block in the positive direction of the `x` axis, stretching the spring until the block stops. When that stopping point is reached, what are (a) the position of the block, (b) the work that has been done on the block by the spring force ? During the block's displacement, what are (d) the block's position when its kinetic energy is maximum and (e) the value of that maximum kinetic energy ?
View SolutionThe force on a particle is directed along an `x` axis and given by `F= F_(0) (x//x_(0)-1)`. Find the work done by the force in moving the particle from `x=0` to `x= 2x_(0)` by (a) plotting `F(x)` and measuring the work from the graph and (b) integrating `F(x)`.
View SolutionA 1.0 kg block is initially at rest on a horizontal frictionless surface when a horizontal force along an `x` axis is applied to the block. The force is given by `vec(F)(x)= (2.5-x^(2)) hat(i)N`, where `x` is in meters and the initial position of the block is `x=0`. (a) What is the kinetic energy of the block as it passes through `x=2.0m` ? (b) What is the maximum kinetic energy of the block between `x=0` and `x=2.0 m` ?
View SolutionA particle of mass 0.020 kg moves along a curve with velocity `5.0 hat(i)+18 hat(k) m//s`. After some time, the velocity changes to `9.0 hat(i) + 22 hat(j)` m/s due to action of a single force. Find the work done on the particle during this interval of time.
View SolutionA can of cookies is made to move along an `x` axis from `x=0.25 m ` to `x= 2.25` m by a force with a magnitude given by `F=` exp `(-4x^(2))`, with `x` in meters and F in newtons. ( Here exp is the exponential function.) How much work is done on the can by the force ?
View SolutionOnly one force is acting on a 2.8 kg particle-like object whose position is given by `x= 4.0t-5.0t^(2)+2.0t^(3)`, with `x` in meters and t in seconds. What is the work done by the force from `t=0` to `t= 6.0` s ?
View SolutionA force of 5.0 N acts on a 15 kg body initially at rest. Compute the work done by the force in (a) the first, (b) the second, and (c) the third seconds and (d) the instantaneous power due to the force at the end of the third second.
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of `12^(@)` with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View SolutionAcross a horizontal floor, a 102 kg block is pulled at a constant speed of 5.5 m/s by an applied force of 125 N directed `38^(@)` above the horizontal. Calculate the rate at which the force does work on the block.
View SolutionThe loaded cab of an elevator has a mass of `5.0 xx 10^(3)` kg and moves 210 m up the shaft in 23 s at constant speed. At what average rate does the force from the cable do work on the cab ?
View SolutionA machine carries a 4.0 kg package from an initial position of `vec(d)_(i)=(0.50 m)hat(i)+(0.75 m)hat(j)+(0.20 m)hat(k)` at `t=0` to a final position of `vec(d)_(f)=(7.50 m)hat(i)+(12.0 m) hat(k)` at `t=12` s. The constant force applied by the machine on the package is `vec(F)= (2.00 N) hat(i) + (4.00 N) hat(j) + (6.00 N) hat(k)`. For that displacement, find (a) the work done on the package by the machine's force and (b) the average power of the machine's force on the package.
View SolutionA fully loaded, slow-moving freight elevator has a cab with a total mass of 1200 kg, which is required to travel upward 54 m in 3.0 min, starting and ending at rest. The elevator's counterweight has a mass of only 950 kg, and so the elevator motor must help. What average power is required of the force the motor exerts on the cab via the cable ?
View Solution(a) At a certain instant, a particle-like object is acted on by a force `vec(F)=(4.0 N) hat(i) - (2.0 N) hat(j) + (9.0 N) hat(k)` while the object's velocity is `vec(v)= -(2.0 m//s) hat(i) + (4.0 m//s) hat(k)`. What is the instan-taneous rate at which the force does work on the object ? (b) At some other time, the velocity consists of only a y component. If the force is unchanged and the instantaneous power is -15 W, what is the velocity of the object ?
View SolutionA force `vec(F)= (3.00 N) hat(i)+(7.00 N) hat(j)+(7.00 N) hat(k)` acts on a 2.00 kg mobile object that moves from an initial position of `vec(d)_(i) = (3.00 m) hat(i)- (2.00 m) hat(j)+ (5.00 m) hat(k)` to a final position of `vec(d)_(f)=-(5.00 m) hat(i) + (4.00 m) hat(j)+ (7.00 m) hat(k)` in 4.00 s. Find (a) the work done on the object by the force in the 4.00 s interval, (b) the average power due to the force during that interval, and (c) the angle between vectors `vec(d)_(i)` and `vec(d)_(f)`.
View SolutionA funny car accelerates from rest through a measured track distance in time T with the engine operating at a constant power P. If the track crew can increase the engine power by a differential amount dP, what is the change in the time required for the run ?
View SolutionAdam stretches a spring by some length. John stretches the same spring later by three times the length stretched by Adam. Find the ratio of the stored energy in the first stretch to that in the second stretch.
View SolutionA 1.50 kg snowball is fired from a cliff 11.5 m high. The snowball's initial velocity is 16.0 m/s, directed to `41.0^(@)` above the horizontal . (a) How much work is done on the snowball by the gravitational force during its flight to the flat ground below the cliff ? (b) What is the change in the gravitational potential energy of the snowball-Earth system during the flight ? (c) If that gravitational potential energy is taken to be zero at the height of the cliff, what is its value when the snowball reaches the ground ?
View Solution(a) In Problem 53, using energy techniques rather than the techniques of Chapter 4, find the speed of the snowball as it reaches the ground below the cliff. What is that speed (b) if the launch angle is changed to `41.0^(@)` below the horizontal and (c) if the mass is changed to 3.00 kg ?
View SolutionA 5.0g marble is fired vertically upward using a spring gun. The spring must be compressed 8.0 cm if the marble is to just reach a target 20 m above the marble's position on the compressed spring. (a) What is the change `DeltaU_(g)` in the gravitational potential energy of the marble-Earth system during the 20 m ascent ? (b) What is the change `DeltaU_(s)` in the elastic potential energy of the spring during its launch of the marble ? (c) What is the spring constant of the spring ?
View SolutionA 700 g block is released from rest at height `h_(0)` above a vertical spring with spring constant `k=450N//m` and negligible mass. The block sticks to the spring and momentarily stops after compressing the spring 19.0 cm. How much work is done (a) by the block on the spring and (b) by the spring on the block ? (c) What is the value of `h_(0)` ? (d) If the block were released from height `2.00h_(0)` above the spring, what would be the maximum compression of the spring ?
View SolutionIn Problem 51, what are the magnitudes of (a) the horizontal component and (b) the vertical component of the net force acting on the block at point Q ? (c) At what height h should the block be released from rest so that it is on the verge of losing contact with rest so that it is on the verge of losing contact with the track at the top of the loop ? (On the verge of losing contact means that the normal force on the block from the track has just then become zero. ) (d) Graph the magnitude of the normal force on the block at the top of the loop versus initial height h, the range `h=0` to `h=6R`.
View SolutionA 1.0 kg block moving at 8.0 m/s strikes a spring fixed at one end to a wall and compresses the spring by 0.40 m, where its speed gets reduced to 2.0 m/s. After this event, the spring is mounted upright by fixing its bottom end to afloor, and a stone of mass 2.0 kg is placed on it, the spring is now compressed by 0.50 m from its rest length. The system is then released. How far above the rest-length point does the stone rise ?
View SolutionA pendulum consists of a 2.0 kg stone swinging on a 4.5 m string of negligible mass. The stone has a speed of 8.0 m/s when it passes its lowest point. (a) What is the speed when the string is at `60^(@)` to the vertical ? (b) What is the greatest angle with the vertical that the string will reach during the stone's motion ? (c) If the potential energy of the pendulum-Earth system is taken to be zero at the stone's lowest point, what is the total mechanical energy of the system ?
View SolutionA block of mass `m=2.0` kg is dropped from height `h=50` cm onto a spring of spring constant `k=1960` N/m ( Fig. 8-68). Find the maximum distance the spring is compressed.

View SolutionAt `t=0` a 1.0 kg ball is thrown from a tall tower with `vec(v)=(18 m//s) hat(i)+(24 m//s) hat(j)`. What is `DeltaU` of the ball-Earth system between `t=0` and `t=6.0s` ( still free fall ) ?
View SolutionA conservative force, `vec(F)=(6.0x-12)hat(i)N`, where `x` is in meters, acts on a particle moving along an `x` axis. The potential energy U associated with this force is assigned a value of 27 J at `x=0`. (a) Write an expression for U as a function of `x`, with U in joules and `x` in meters. (b) What is the maximum positive potential energy ? At what (c) negative value and (d) positive value of `x` is the potential energy equal to zero ?
View SolutionIn Fig. 8-73, a chain is held on a frictionless table with one-fourth of its length hanging over the edge. If the chain has length `L=24` cm and mass `m=0.016` kg, how much work is required to pull the hanging part back onto the table ?

View SolutionA uriform chain hangs over the edge of a horizontal platform. A machine does 1.0 J of work in pulling the rest of the chain onto the platform. The chain has a mass of 2.0 kg and a length of 3.0 m. What length was initially hanging over the edge ? On the Moon, the gravitational acceleration is 1/6 of `9.8 m//s^(2)`.
View SolutionA worker pushed a 23 kg block 8.4 m along a level floor at constant speed with a force directed `32^(@)` below the horizontal . If the coefficient of kinetic friction between block and floor was 0.20, what were (a) the work done by the worker's force and (b) the increase in thermal energy of the block-floor system ?
View SolutionIn Fig. 8-78, a 3.5 kg block is accelerated from rest by a compressed spring of spring constant 640 N/m. The block leaves the spring a the spring's relaxed length and then travels over a horizontal floor with a coefficient of kinetic friction `mu_(g)=0.25`. The frictional force stops the block in distance `D=7.8m`. What are (a) the increase in the thermal energy of the block-floor system, (b) the maximum kinetic energy of the block, and (c) the original compression distance of the spring ?

View SolutionA horizontal force of magnitude 41.0 N pushes a block of mass 4.00 kg across a floor where the coefficient of kinetic friction is 0.600. (a) How much work is done by that applied force on the block-floor system when the block slides through a displacement of 2.00 m across the floor ? (b) During that displacement, the thermal energy of the block increases by 40.0 J. What is the increase in thermal energy of the floor ? (c) What is the increase in the kinetic energy of the block ?
View SolutionAn outfielder throws a baseball with an initial speed of 83.2 mi/h. Just before an infielder catches the ball at the same level, the ball's speed is 110 ft/s. In foot-pounds, by how much is the mechanical energy of the ball-Earth system reduced of air drag ? (The weight of a baseball is 9.0 oz.)
View SolutionA 60 kg skier leaves the end of a ski-jump ramp with a velocity of 27 m/s directed `25^(@)` above the horizontal. Suppose that as a result of air drag the skier returns to the ground with a speed of 22 m/s, landing 14 m vertically below the end of the ramp. From the launch to the return to the ground, by how much is the mechanical energy of the skier-Earth system reduced because of air drag ?
View SolutionA large fake cookie sliding on a horizontal surface is attached to one end of a horizontal spring with spring constant `k=360` N/m, the other end of the spring is fixed in place. The cookie has a kinetic energy of 20.0 J as it passes through the spring's equilibrium position. As the cookie slides, a frictional force of magnitude 10.0 N acts on it . (a) How far will the cookie slide from the equilibrium position before coming momentarily to rest ? (c) What will be the kinetic energy of the cookie as it slides back through the equilibrium position ?
View SolutionA swimmer moves through the water at an average speed of 0.22 m/s. The average drag force is 110 N. What average power is required of the swimmer ?
View SolutionA child whose weight is 267 N slides down a 6.5 m playground slide that makes an angle of `20^(@)` with the horizontal. The coefficient of kinetic friction between slide and child is 0.10 (a) How much energy is transferred to thermal energy ? (b) If she starts at the top with a speed of 0.457 m/s, what is her speed at the bottom ?
View SolutionThe total mechanical energy of a 2.00 kg particle moving along an x axis is 5.00 J. The potential energy is given as `U(x)=(x^(4)-2.00x^(2))J`, with x in meters. Find the maximum velocity.
View SolutionYou push a 2.0 kg block against a horizontal spring , compressing the spring by 12 cm. Then You release the block, and the spring sends it sliding across a tabletop. It stops 75 cm from where you released it. The spring constant is 170 N/m. What is the block-table coefficient of kinetic friction ?
View SolutionA block of mass 6.0 kg is pushed up an incline to its top by a man and then allowed to slide down to the bottom. The length of incline is 10 m and its height is 5.0 m. the coefficient of friction between block and incline is 0.40. Calculate (a) the work done by the gravitational force over the complete round trip of the block, (b) the work done by the man during the upward journey, (c) the mechanical energy loss due to friction over the round trip, and (d) the speed of the block when it reaches the bottom.
View SolutionA cookie jar is moving up a `40^(@)` incline. At a point 45 cm from the bottom of the incline ( measured along the incline ) ,the jar has a speed of 1.4 m/s. The coefficient of kinetic friction between jar and incline is 0.15 . (a) How much farther up the incline will the jar move ? (b) How fast will it be going when it has slid back to the bottom of the incline ? (c) Do the answers to parts (a) and (b) increase, decrease, or remain the same if we decrease the coefficient of kinetic friction ( but do not change the given speed or location ) ?
View SolutionA stone with a weight of 5.29 N is launched vertically from ground level with an initial speed of 20.0 m/s, and the air drag on it is 0.265 N throughout the flight. What are (a) the maximum height reached by the stone and (b) its speed just before it hits ground ?
View SolutionA 4.0 kg bundle starts up a `30^(@)` incline with 150 J of kinetic energy. How far will it slide up the incline if the coefficient of kinetic friction between bundle and incline is 0.36 ?
View SolutionA 10.0 kg block falls 30.0 m onto a vertical spring whose lower end is fixed to a platform. When the spring reaches its maximum compression of 0.200 m, it is locked in place. The block is then removed and the spring apparatus is transported to the Moon, where the gravitational acceleration is g/6. A 50.0 kg astronaut then sits on top of the spring and the spring is unlocked so that it propels the astronaut upward. How high above that initial point does the astronaut rise ?
View Solution
PROBLEMS questions and complete solutions for chapter WORK, POWER, AND ENERGY of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12