Complete Solutions to PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE) of chapter RIGID BODY DYNAMICS - I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS - I |
| RESNICK AND HALLIDAY | PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE) |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
A hoop of radius `r` mass `m` rotating with an angular velocity `omega_(0)` is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionThe Earth takes slightly less than one day to complete one rotation about the axis passing through its poles. The actual time is `8.616xx10^(4)`s. With this given information, what is the angular speed of the Earth about its axis?
View SolutionA marble and a cube are placed at the top of a ramp. Starting from rest at the same height, the marble rolls and the cube slides (no kinetic friction) down the ramp. Determine the ratio of the center-of-mass speed of the cube to the center-of-mass speed of the marble at the bottom of the ramp.
View SolutionA wheel with a 0.10 m radius is rotating at 35 rev/s. It then slows uniformly to 15 rev/s over a 3.0 s interval. What is the angular acceleration of a point on the wheel?
View SolutionA body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
View SolutionDuring the spin-dry cycle of a washing machine, the motor slows from 95 rad/s to 30 rad/s while the turning the drum through an angle of 402 rad. What is the magnitude of the angular acceleration of the motor?
View SolutionTwo people start at the same place and walk around a circular lake in opposite directions. One has an angular speed of `1.7xx10^(-3)` rad/s while the other has an angular speed of `3.4xx10^(-3)` rad/s. How long will it be before they meet?
View SolutionA fan rotating with an initial angular velocity of 1000 rev/min is switched off. In 2s, the angular velocity decreases to 200 rev/min. Assuming the angular acceleration is constant, how many revolutions does the blade undergo during this time?
View SolutionA basketball player is balancing a spinning basketball on the tip of his finger. The angular velocity of the ball slows down from 18.5 to 14.1 rad/s. During the slow-down, the angular displacement is 85.1 rad. Determine the time it takes for the ball to slow down.
View SolutionAn airplane engine starts from rest, and 2 s later, it is rotating with an angular speed of 300 rev/min. If the angular acceleration is constant, how many revolutions does the propeller undergo during this time?
View SolutionIn 9.5 s a fisherman winds 2.6 m of fishing line onto a reel whose radius is 3.0 cm (assumed to be constant as an approximation). The line is being reeled in at a constant speed. Determine the angular speed of the reel.
View SolutionDuring the time a CD accelerates from rest to a constant rotational speed of 477 rev/min, it rotates through an angular displacement of 0.250 rev. What is the angular acceleration of the CD?
View SolutionA person is riding a bicycle, and its wheels have an angular velocity of +20.0 rad/s Then, the brakes are applied, and the bike is brought to a uniform stop. During braking, the angular displacement of each wheel is +15.92 rev. How much time does it take for the bike to come to rest?
View SolutionA grindstone, initially at rest, is given a constant angular acceleration so that it makes 20.0 rev in the first 8.00 s. What is its angular acceleration?
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity `omega`. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA wheel turns through an angle of 188 rad in 8.0 s, and its angular speed at the end of the period is 40 rad/s. If the angular acceleration is constant, what was the angular speed of the wheel at the beginning of the 8.0 s interval?
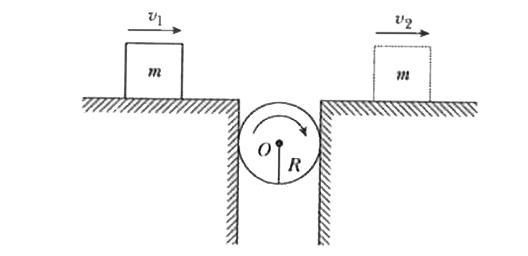
View SolutionA uniform disc of mass M and radius R is initially at rest. Its axis is fixed through O. A block of mass m is moving with speed `v_(1)` on a frictionless surface passes over the disc to the dotted position. On coming in contact with the disc, it slips on it. The slipping ceases before the block loses contact with the disc, due to the high friction. Now, the velocity of mass m is
View SolutionA 1.0 m roulette wheel reaches a maximum angular speed of 18 rad/s before it begins decelerating. After reaching this maximum angular speed, it turns through 35 rev (220 rad) before it stops. How long did it take the wheel to stop after reaching its maximum angular speed?
View SolutionA ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
View SolutionA circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
View SolutionAfter 10.0 s, a spinning roulette wheel at a casino has slowed down to an angular velocity of +1.88 rad/s. During this time, the wheel has an angular acceleration of `-5.04rad//s^(2)`. Determine the angular displacement of the wheel.
View SolutionA circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of `20.0rad//s^(2)`. What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
View SolutionAt the local swimming hole, a favorite trick is to run horizontally off a cliff that is 8.3 m above the water. One diver runs off the edge of the cliff, tucks into a ball, and rotates on the way down with an average angular speed of 1.6 rev/s. Ignore air resistance and determine the number of revolutions she makes while on the way down.
View SolutionThe original Ferris wheel has a radius of 38 m and completed a full revolution (`2pi` rad) every two minutes when operating at its maximum speed. If the wheel were uniformly slowed from its maximum speed to a stop in 35 s, what would be the magnitude of the tangential acceleration at the outer rim of the wheel during its deceleration?
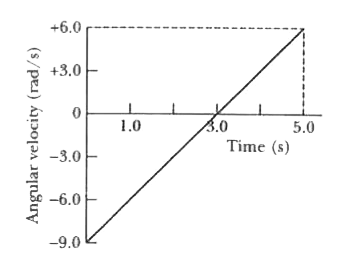
View SolutionThe figure shows a graph of the angular velocity of a rotating wheel as a function of time. Although not shown in the graph, the angular velocity continues to increase at the same rate until t = 8.0 s. What is the angular displacement of the wheel from 0 to 8.0 s?
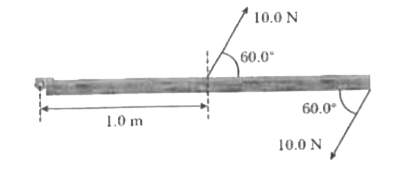
View SolutionThe figure shows the top view of a door that is 2 m wide. Two forces are applied to the door as indicated. What is the magnitude of the net torque on the door with respect to the hinge?
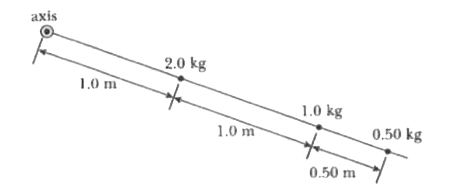
View SolutionThree objects are attached to a massless rigid rod that has an axis of rotation an shown. Assuming all of the mass of each object is located at the point shown for each, calculate the moment of inertia of this system.
View SolutionA solid circular disk has a mass of 1.2 kg and a radius of 0.16 m. Each of three identical thin rods has a mass of 0.15 kg. The rods are attached perpendicularly to the plane of the disk at its outer edge to form a three-legged stool. Find the moment of inertia of the stool with respect to an axis that is perpendicular to the plane of the disk at its center.

View SolutionA 50 kg rider on a moped of mass 75 kg is traveling with a speed of 20 m/s. Each of the two wheels of the moped has a radius of 0.2 m and a moment of inertia of `0.2kg*m^(2)`. What is the total rotational kinetic energy of the wheels?
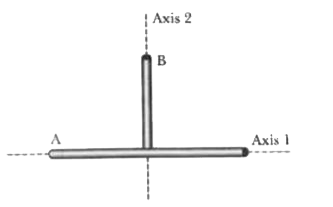
View SolutionA long thin rod is cut into two pieces, one being twice as long as the other. To the midpoint of piece A (the longer piece), piece B is attached perpendicularly, in order to form the inverted "T" as shown in the figure. The application of a net external torque causes this object to rotate about axis 1 with an angular acceleration of `4.6"rad"//s^(2)`. When the same net external torque is used to cause the object to rotate about axis 2, what is the angular acceleration?
View SolutionA 50 N m torque acts on a wheel with a moment of inertia `150kg*m^(2)`. If the wheel starts from rest, how long will it take the wheel to make 1 rev?
View SolutionA solid cylinder of radius 0.35 m is released from rest from a height of 1.8 m and rolls down the incline as shown in the figure. What is the angular speed of the cylinder when it reaches the horizontal surface?

View SolutionOne end of a thin rod is attached to a pivot, about which it can rotate without friction. Air resistance is absent. The rod has a length of 0.80 m and is uniform. It is hanging vertically straight downward. The end of the rod nearest the floor is given a linear speed `v_(0)`, so that the rod begins to rotate upward about the pivot. What must be the value of `v_(0)`, such that the rod comes to a momentary halt in a straight-up orientation, exactly opposite to its initial orientation?
View SolutionA thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as `k((x)/(L))^n` where n can be zero or any positive number. If the position `X_(CM)` of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of `X_(CM)` on n?
View SolutionA solid cylinder with a mass m and radius r is mounted so that it can be rotated about an axis that passes through the center of both ends. At what angular speed, `omega` must the cylinder rotate to have the same total kinetic energy that it would have if it were moving horizontally with a speed v without rotation?
View SolutionA point P moves in counter-clockwise direction on figure. The movement of P is such that it sweeps out a length `s=t^(3)+5`, where s is in metre and t is in second. The radius of the pathh is 20 m. the acceleration of P when t=2s is nearly
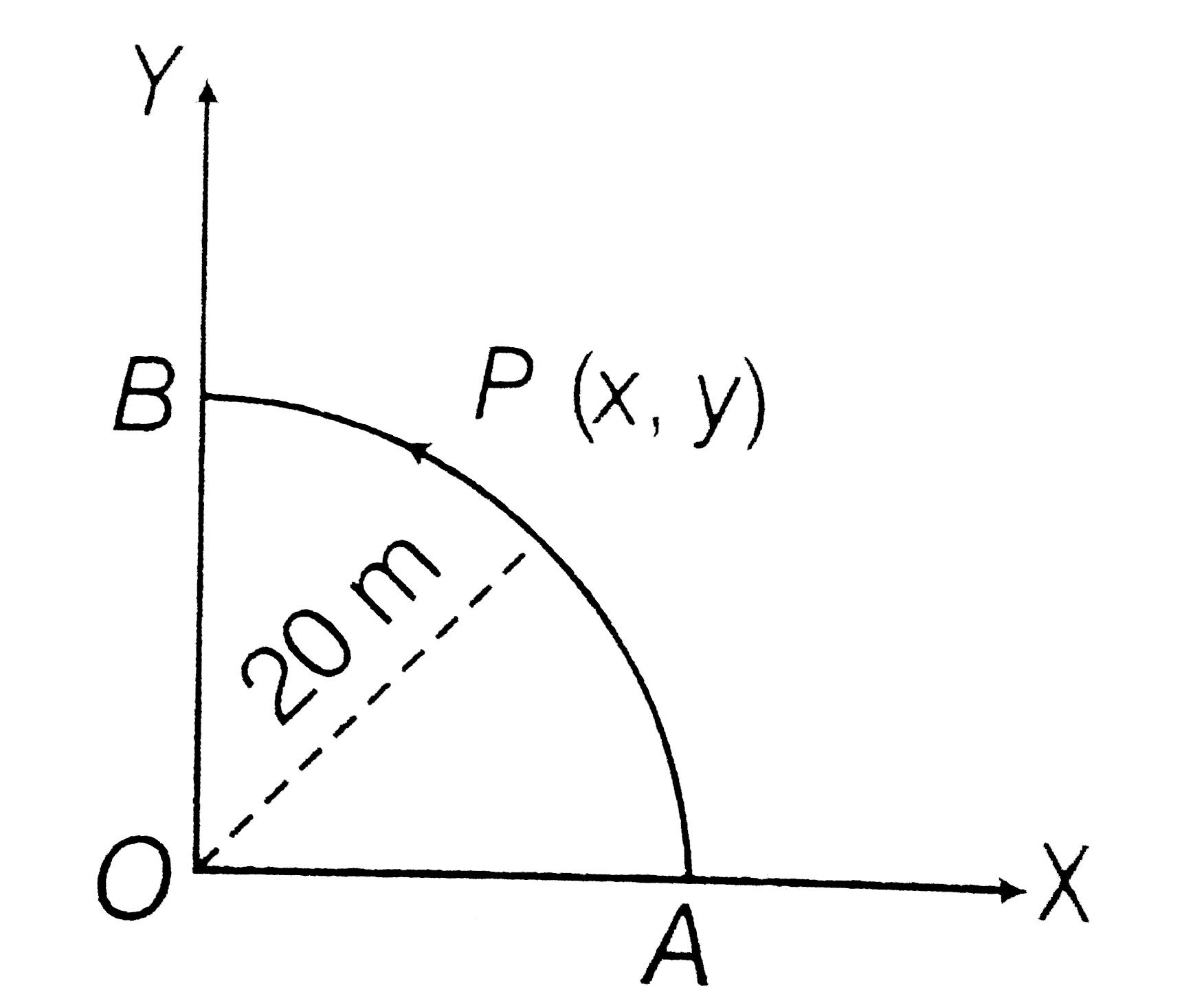
View SolutionA certain merry-go-round is accelerated uniformly from rest and attains an angular speed of 0.4 rad/s in the first 10 s. If the net applied torque is 2000 `N*m`, what is the moment of inertia of the merry-go-round?
View SolutionA body is rotating around a fixed axis with angular velocity 3 rad/s with constant angular acceleration of `1rad//s^(2)` at some time. Find the magnitude of acceleration of a particle 5 m away from the axis after the body has turned by `90^(@)`.
View SolutionA 1.0 kg wheel in the form of a solid disk rolls along a horizontal surface with a speed of 6.0 m/s. What is the total kinetic energy of the wheel?
View SolutionMoment of inertia of a half ring of mass `m` and radius `R` about an axis passing through point `A` perpendicular to the plane of the paper is `I_(A)`. If `I_(C )` is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point `C`, then

View SolutionWhich one of the following statements concerning the moment of inertia I is false?
View SolutionConsider the following four objects:
(i) a hoop
(ii) a flat disk
(iii) a solid sphere
(iv) a hollow sphere
Each of the objects has mass M and radius R. The axis of rotation passes through the center of each object and is perpendicular to the plane of the hoop and the plane of the flat disk. Which object requires the largest torque to give it the same angular acceleration?
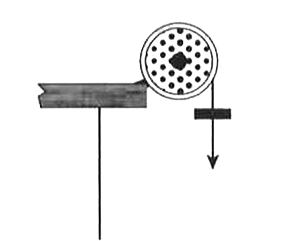
View SolutionA 45 N brick is suspended by a light string from a 2.0 kg pulley. The brick is released from rest and falls to the floor below as the pulley rotates through 5.0 rad. The pulley may be considered a solid disk of radius 1.5 m. What is the angular speed of the pulley?
View Solution
PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE) questions and complete solutions for chapter RIGID BODY DYNAMICS - I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12