Complete Solutions to SAMPLE PROBLEM of chapter RIGID BODY DYNAMICS - I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS - I |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
The disk in Fig. 10-5a is rotating about its central axis like a merry-go-round. The angular position `theta(t)` of a reference line on the disk is given by
`theta=-1.00-0.600t+0.250t^(2)`,
with t in seconds, `theta` radians, and the zero angular position as indicated in the figure.
(a) Graph the angular position of the disk verus time from t = -3.0 s to t = 5.4 s. Sketch the disk and its angular position reference line at t = -2.0 s, 0 s, and 4.0 s, and when the curve crosses the t axis.
(b) At what time `t_(min)" does "theta(t)` reach the minimum value shown in Fig. 10-5b? What is that minimum value?
(c ) Graph the angular velocity `omega` of the disk versus time from t = -3.0 s to t = 6.0 s. Sketch the disk and indicate the direction of turning and the sign of `omega` at t = -2.0 s, 4.0 s, and `t_(min)`.
(d) Use the results in parts (a) through ( c) to describe the motion of the disk from t = -3.0 s to t = 6.0 s.
View SolutionA child's top is spun with angular acceleration
`alpha=5t^(3)-4t`,
with t in seconds and `alpha` in radians per second-squared. At t = 0, the top has angular velocity 5 rad/s, and a reference line on it is at angular position `theta=2` rad.
(a) Obtain an expression for the angular velocity `omega(t)` of the top. That is, find an expression that explicitly indicates how the angular velocity depends on time.
(b) Obtain an expression for the angular position `theta(t)` of the top.
View SolutionA grindstone rotates at constant angular acceleration `alpha=0.35rad//s^(2)`. At time t = 0, it has an angular velocity of `omega_(0)=-4.6rad//s` and a reference line on it is horizontal, at the angular position `theta_(0)=0`.
(a) At what time after t = 0 is the reference line at the angular position `theta=5.0 ` rev ?
(b) Describe the grindstone's rotation between t = 0 and t = 32 s.
(c) At what time t does the grindstone momentarily stop?
View SolutionWhile you are operating a Rotor (a large, vertical, rotating cylinder found in amusement parks), you spot a passenger in acute distress and decrease the angular velocity of the cylinder from 3.40 rad/s to 2.00 rad/s in 20.0 rev, at constant angular acceleration. (The passender is obviously more of a "translation person" than a "rotation person.")
(a) What is the constant angular acceleration during this decrease in angular speed?
How much time did the speed decrease take?
View SolutionWe are given the job of designing a large horizontal ring that will rotate around a vertical axis and that will have a radius of r = 33.1 m. Passengers will enter through a door in the outer wall of the ring and then stand next to that wall. We decide that for the time interval t = 0 to t = 2.30 s, the angular position `theta(t)` of a reference line on the ring will be given by
`theta=ct^(3)`,
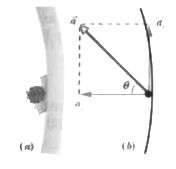
with `c=6.39xx10^(-2)rad//s^(3)`. After t = 2.30 s, the angular speed will be held constant until the end of the ride. Once the ring begins to rotate, the floor of the ring will drop away from the riders but the riders will not fall - indeed, they feel as though they are pinned to the wall. For the time t = 2.20 s, let's determine a rider's angular speed `omega`, linear speed `nu`, angular acceleration `alpha`, tangential acceleration `a_(t)`, radial acceleration `a_(r)`, and acceleration `veca`.
View SolutionFigure a rigid body consisting of two particles of mass m connected by a rod of length L and negligible mass.
(a) What is the rotational inertia `I_(com)` about an axis through the center of mass, perpendicular to the rod as shown?
(b) What is the rotational inertia I of the body about an axis through the left end of the rod and parallel to the first axis.
View SolutionFigure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View SolutionLarge machine components that undergo prolonged, high-speed rotation are first examined for the possibility of failure in a spin test system. In this system, a component is spun up while inside a cylindrical arrangement of lead bricks and containment liner, all within a steel shell that is closed by a lid clamped into place. If the rotation causes the component to shatter, the soft lead bricks are supposed to catch the pieces for later analysis.
In 1985, Test Devices, Inc. was spin testing a sample of a solid steel rotor of mass M = 272 kg and radius R = 38.0 cm. When the sample reached an angular speed `omega` of 14000 rev/min, the test engineers heard a dull thump from the test system, which was located one floor down and one room over from them. Investigating, they found that lead bricks had been thrown out in the hallway leading to the test room, a door to the room had been hurled into the adjacent parking lot, one lead brick had shot from the test site through the wall of a neighbor's kitchen, the structural beams of the test building had been damaged, the concrete floor beneath the spin chamber had been shoved downward by about 0.5 cm, and the 900 kg lid had been blown upward through the ceiling and had then crashed back onto the test equipment. The exploding pieces had not penetrated the room of the test engineers only by luck. How much energy was released in the explosion of the rotor?
View SolutionFind the moment of inertia of a uniform rign of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
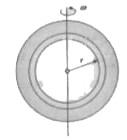
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionFind moment of inertia of a uniform rectangular plate about axis zz' passing through center and perpendicular to the plane of plate, as shown in Fig.

View SolutionIn Fig., three forces, each of magnitude 2.0 N, act on a particle. The particle is in the xz' plane at point A given by position vector `vecr`, where r = 3.0 m and `theta=30^(@)`. What is the torque, about the origin O, due to each force?
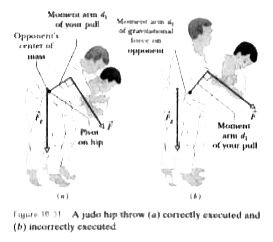
View SolutionTo throw an 80 kg opponent with a basic judo hip throw, you intend to pull his uniform with a force `vecF` and a moment arm `d_(1)` = 0.30 m from a pivot point on your right hip. You wish to rotate him about the pivot point with an angular acceleration `alpha" of "-6.0rad//s^(2)` - that is, with an angular acceleration that is clockwise in the figure. Assume that his rotational inertia I relative to the pivot point is `15kg*m^(2)`.
(a) What must the magnitude of `vecF` be if, before you throw him, you benf your opponent forward to bring his center of mass to your hip?
(b) What must the magnitude of `vecF` be if your opponent remains upright before you throw him, so that `vecF_(g)` has a moment arm `d_(2)=0.12m`?
View SolutionFigure shows a uniform disk, with mass M = 2.5 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block with mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. Find the acceleration of the falling block, the angular acceleration of the disk, and the tension in the cord. The cord does not slip, and there is no friction at the axle.
View SolutionLet the disk of mass 2.5kg start from rest at time t = 0 and also let the tension in the massless cord be 6.0 N and the angular acceleration of the disk be `-24rad//s^(2)`. What is its rotational kinetic energy K at t = 2.5 s?
View SolutionA tall, cylindrical chimney starts falling over as shown in Fig. Treat the chimney as a thin rigid rod of length L = 55.0 m. At the instant it makes as angle of `theta=60.0^(@)`m with the vertical, what is its angular speed `omega_(f)`?
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle `theta` as shown in Fig.
View SolutionFigure shows an overhead view of two particles moving at constant momentum along horizontal paths.
Particle 1, with momentum magnitude `p_(1)=5.0kg*m//s`, has position vector `vecr_(1)` and will pass 2.0 m from point O.
Particle 2, with momentum magnitude `p_(2)=2.0kg*m//s`, has position vector `vecr_(2)` and will pass 4.0 m from point O. What are the magnitude and direction of the net angular momentum `vecL` about point O of the two particle system?
View SolutionFigure shows a freeze-frame of a 0.500 kg particle moving along a straight line with a position vector given by
`vecr=(-2.00t^(2)-t)hati+5.00hatj`,
With `vecr` in meters and t in seconds, starting at t = 0. The position vector points from the origin to the particle. In unit-vector notation, find expressions for the angular momentum `vecl` of the particle and the torque `vectau` acting on the particle, both algebraic signs in terms of the particle's motion.
View SolutionThe original Ferris wheel was built in 1893 by George Washington Gale Ferris, Jr., a civil engineering. The wheel, an amazing engineering construction at the time, carried 36 wooden cars, each holding as many as 60 passengers, around a circle of radius R = 38 m. The mass of each car was about `1.1xx10^(4)kg`. The mass of the wheel's structure was about `6.0xx10^(5)kg`, which was mostly in the circular grid from which the cars were suspended. The wheel made a complete rotation at an angular speed `omega_(F)` in about 2 min.
(a) Estimate the magnitude L of the angular momentum of the wheel and its passengers while the wheel rotated at `omega_(F)`.
(b) If the fully loaded wheel is rotated from rest to `omega_(F)` in a time period `Deltat_(1)=5.0s`, what is the magnitude `t_(avg)` of the avergae net external torque acting on it?
View SolutionThe conical pendulum is in steady circular motion with constant angular velocity `omega` as shown in Fig. Mass of the particle is M and string makes angle `alpha` with vertical.
(a) Find angular momentum of the particle about the center C of the circle and the hinge O about which the string is attached.
(b) Also check whether L is changing or is constant.
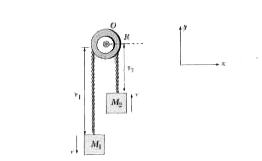
View SolutionA block of mass `M_(1)` and a block of mass `M_(2)` are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.
View SolutionFigure shows a student, again sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose rotational inertia `I_(wh)` about its central axis is `1.2kg*m^(2)`.
The wheel is rotating at an angular speed `omega_(wh)` of 3.9 rev/s, as seen from overhead, the rotation is counterclockwise. The axis of the wheel is vertical, and the angular Momentum `vecL_(wh)` of the wheel points vertically upward.
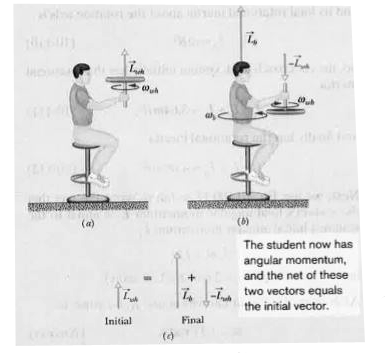
The student now inverts the wheel so that, as seen from overhead, it is rotating clockwise. Its angular momentum is now `-vecL_(wh)`. The inversion results in the student, the stool, and the wheel's center rotating together as a composite rigid body about the stool's rotation axis, with rotational inertia `I_(b)=6.8kg*m^(2)`. With what angular speed `omega_(b)` and in what direction does the composite body rotate after the inversion of the wheel?
View SolutionIn Fig. a cockroach with mass m rides on a disk of mass 6.00 m and radius R. The disk rotates like a merry-go-round around its central axis at angular speed `omega_(i)=1.50rad//s`. The cockroach is initially at radius r = 0.800R, but then it crawls out to the rim of the disk. Treat the cockroach as a particle. What then is the angular speed?
View SolutionOn a horizontal smooth plane there is a fixed vertical cylinder and a particle A connected to the cylinder by a thread AB. The particle is set in motion with the initial velocity v as shown in the figure. Is there any fixed point relative to which the angular

momentum of the particle is constant in the process of motion?
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity `omega_(1)`. Disk 2 rotating with the angular velocity `omega_(2)` is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to `I_(1)andI_(2)`, respectively. The constant surface of the disks are rough.
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
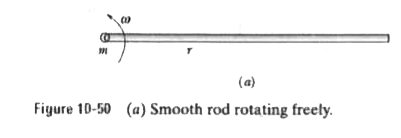
View SolutionA uniform rod of mass m and length l is hinged about one of its end. The hinge is smooth and rod lies on a smooth horizontal surface as shown in Fig. A particle of mass m is coming towards the rod at speed `v_(0)` perpendicular to the length of rod.
(a) Find angular velocity of the rod just after impact.

(b) Also find impulse due to hinge on rod during collision.
View SolutionA horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity `omega_(0)` of the cylinder, the speed `v_(0)` of the falling body of mass m, and the kinetic energy `K_(0)` of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, `omega_(1),v_(1),andK_(1)`, for the instant just after the string becomes taut.
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter RIGID BODY DYNAMICS - I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12