Complete Solutions to PHYSICS of chapter TS EAMCET 2019 (6 MAY SHIFT 1) of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | TS EAMCET 2019 (6 MAY SHIFT 1) |
| TS EAMCET | PHYSICS |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
Match the following table.

View SolutionConsider a spongy block of mass m floating on a flowing river. The maximum mass of the block is related to the speed of the river flow v, acceleration due to gravity g and the density of the block `rho` such that `m_(max)=kv^(x)g^(y)rhz^(z)` (k is constant). The values of x, y and z should then respectively be (Mass of the spongy block is assumed to vary due to absorption of water by it)
View SolutionA ball is thrown vertically upward from the ground at time t=0 s. It passes the top of a tower at t=3 s and 2 s later it reaches and its maximum height. The height of the tower is (Acceleration due to gravity, `g=10m//s^(2))`
View SolutionRain is falling vertically with a speed of 30 m/s. from East to West direction. At what the angle with the vertical, he sees the rain falling?
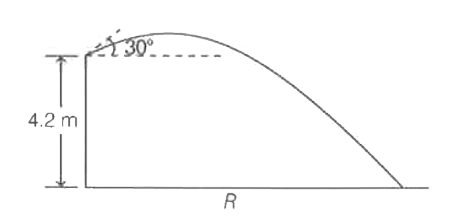
View SolutionAn archer shoots an arrow from a height 4.2 m above the ground with a speed 40 m/s and at angle `30^(@)` as shown in the figure. Determine the horizontal distance R covered by the arrow, when it hits the ground, (Take `g=10m//s^(2))`
View SolutionA bullet enters a wooden block with velocity 120 m/s. The bullet travels 1.5 s in the block before its velocity reduces to zero due to resistance force which is proportional to the square root of the velocity. The distance travelled by the bullet in the wooden block is
View SolutionA bouncing ball of mass 200 g falls from the height of 5m on a horizontal ground. After every impact with the ground, the velocity of the ball decreases by `(1)/(2)` times. The total momentum the ball imparts on to the ground after 3 impacts is (Let `g=10m//s^(2)`)
View SolutionA block of mass 100 g is suspended vertically from a massless spring system of spring constant, k=1 N/m each. The block is hit from above to impart an impulse of 2 Ns. Calculate the maximum displacement from the Equilibrium position of the block. (Take, `g=10m//s^(2)`)
View SolutionA metal chain of mass 2 kg and length 90 cm over hangs a table with 60 cm on the table. How much work needs to be done to put the hanging part of the chain back on the table? (Let `g=10m//s^(2)`)
View SolutionA thin circular disc of mass 12 kg and radius 0.5 m rotates with an angular velocity of 100 rad/s. The rotational kinetic energy of the disc is
View SolutionThe distance between Sum and Earth is `1.6xx10^(11)` m and the radius of Earth is `6.4xx10^(6)`m. The ratio of the angular momentum of Earth around the Sum to the angular momentum around its own axis is approximately (Assume Earth as a solid sphere with uniform mass density and rotates around the Sum in a circular path.)
View SolutionA uniform rod of length 1.8 m suspended by an end is made to undergo small oscillations. Find the length of the simple pendulum having the mass and time period equal to that of the rod.
View SolutionA planet of mass m moves around the Sum along an elliptical path with a period of revolution T. During the motion, the planet's maximum and minimum distance from Sum is R and `(R)/(3)` respectively. If `T^(2)=alphaR^(3)`, then the magnitude of constant `alpha` will be
View SolutionA copper wire and an aluminium wire have lengths in the ratio 5:2 diameters in the ratio 4:3 and forces applied in the ratio 4:5. Find the ratio of increase in length of the copper wire to that aluminium wier. (Let `Y_(Cu)=1.1xx10^(11)Nm^(-2),Y_(Al)=0.7xx10^(11)Nm^(-2)`)
View SolutionConsider a water droplet of diameter 0.2 mm where the outside pressure is `1.5N//cm^(2)` at `25^(@)C`. The pressure inside the droplet, when the surface tension at `25^(@)C` is 0.08 N/m is
View SolutionA hydrophilic surface is characterised by the contact angle at the water soled interface. The value of contact angle should be
View SolutionThe temperature of body is increased from `T_(1)=127^(@)C" to "T_(2)=227^(@)C`. The ambient temperature is `27^(@)`C. The energies emitted per second by the body at `T_(1)andT_(2)` are `E_(1)andE_(2)` respectively. The ratio of `(E_(2))/(E_(1))` is
View SolutionTwo thin metallic spherical shells of radii 20 cm and 30 cm, respectively are placed with their centres coinciding. A material of thermal conductivity `alpha` is filled in the space between the shells. The inner shell is maintained at 300 K and the outer shell at 310 K. If the rate at which heat flows radially through the material is 40 W, find the value of `alpha` (in units of `Js^(-1)m^(-1)K^(-1)`).
View SolutionPressure at the Earth's surface is `p_(a)=10^(5)Pa` and the density of air at Earth's surface is `rho_(0)=1.4kg//m^(3)`. At height h from the surface of Earth the density of air is reduced to `(rho_(0))/(2)` the value of h is (Assume that the temperature is constant through out the earth's atmosphere and let In (2)=0.7)
View SolutionConsider an ideal gas at pressure p, volume V and temperature T. The mean free path for molecules of the gas is L. If the radius of gas molecules, as well as pressure, volume and temperature of the gas are doubled, then the mean free path will be
View SolutionTwo identical sinusoidal waves are moving in the same direction along a stretched string, interfere with each other. The phase difference between them is `120^(@). The amplitudes of both the waves are same. If the amplitude of the resultant wave due to interfernce is 2mm, the amplitude of each wave is
View SolutionA whistle of frequency 660 Hz moves in a circle of radius 1 m at an angular speed of 10 rad/s. The highest frequecny heard by a listener at a long distance and at rest with respect to the center of the circle is (Let speed of sound =340 m//s.)
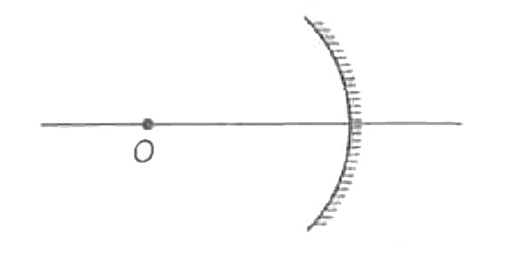
View SolutionAn object O is placed at 7 cm to the left of a concave mirror of raidus of curvature 12 cm as shown in the figure. The position of the image will be at a distance of
View SolutionLight consisting of a plane waves of wavelength, `lamda_(1)=8xx10^(-5)cmandlamda_(2)=6xx10^(-5)cm` generates an interference pattern in Young's double slit experiment. If `n_(1)` denotes the `n_(1)` th dark fringe due to light of wavelength `lamda_(1)` which coincides with `n_(2)` th bright fringe due to light of wavelength `lamda_(2)`, then
View SolutionA spherical valume contains a unifromly distributed charge of density `1.0xx10^(-6)C//m^(3)`. Find the electrical field (in N/C) at a point inside the volume at a distance 1 mm from the centre. `("Let "(1)/(4piin_(0))=9xx10^(9)Nm^(2)C^(-2))`
View SolutionFour identical metal plates each of area A are separated mutually by a distance d and are connected as shown. Find the capacity of the system between the terminals A and B.

View SolutionThe resistance of a device component decreases as the current through it increases and it is described by the relation, `R=(0.2I)/(I-4)`, where I is the current. Determined the minimum power deliver. (Assume, `Igt4`)
View SolutionA 100 W tungsten light bulb has a resistance of `250Omega` when it as turned ON and `25Omega` when turned OFF. The ambient room temperture is `25^(@)C`. Find the temperature of the filament when the bulb is turned ON, ( Let `alpha_("tungsten")=4.5xx10^(-3)//^(@)C`)
View SolutionTwo paraticles carrying equal charges move parallel to each other with the speed 150 km/s. If `F_(1)andF_(2)` are magnetic and electric forces between two charged particles then, `(|F_(1)|)/(|F_(2)|)` is `("Let "mu_(0)epsi_(0)=(1)/(9xx10^(16))S^(2)//m^(2))`
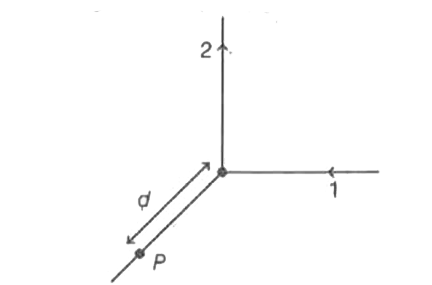
View SolutionA very long wire carrying a current `4sqrt2` A is bent at a right angles. The magnitude of magnetic field `(|B|)` at a point P lying on a line perpendicular to the bent wire at a distance, d=20 cm from the point of the bending will be (Let `mu_(0)=4pixx10^(-7)H//m`)
View SolutionIdentify the incorrect statement from the following.
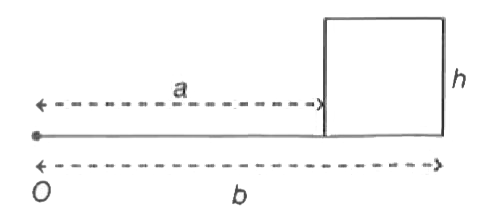
View SolutionConsider a toroid with rectangular cross section, of inner radius a, outer radius be and height h, carrying n number of turns. Then the self-inductance of the toroidal coil when current I passing through the toroid is
View SolutionA coil is connected to an AC source with peak emf, 8 V and frequency `(30)/(pi)`Hz. The coil has resistance of `8Omega`. If the average power dissipated by the coil is 0.4 W, then the inductance of the coil is
View SolutionA flashlight of intensity 9 W/`cm^(2)` illuminates a perfectly reflective surface of area `300cm^(2)`. The average force exerted on the surface due to the incident light photons is
View SolutionA parallel beam of monochromatic light of frequency v is indcident on a surface. The intensity of the beam is I and area of the surface is A. Find the force exerted by light of beam on the surface is perfectly reflecting and the light beam is incident at an angle of incidence `theta`. (The speed of light is denoted as c.)
View SolutionMonochromatic radiation is incident on hydrogen (H) sample which is in ground state. If the hydrogen atoms emit radiation of ten different wavelengths after absorbing the incident radiation, then the wavlength of the incident radiation is (Let `hc=1242eV-nm`)
View SolutionTwo radioactive materials `R_(1)andR_(2)` have deacy constants `6lamdaandlamda` respectively. The half life of `R_(2)" is "1.4xx10^(17)` s. Initially they contain some number of nuclei.
The time at which the ratio of the remaining nuclei of `R_(2)` to that of `R_(1)` will be e is (Let In 2=0.7)
View SolutionA person applies a sine wave and square wave to an AND gate as shown in the figure (i) and (ii). Assuming that both the voltages are applied in phase, the person observes the output at E and F on (i) and (ii), respectively. [Assume minimun voltage of 5 V is equivalent to logic (i)]
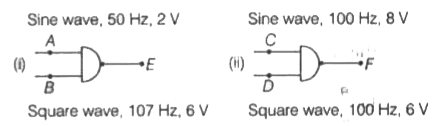
View SolutionConsider an amplifier circuit in which a transistor is used in common-emitter mode. The load resistance `3kOmega`. When, a signal of 30 mV is added to base emitter voltage, the base current is changed by `30muA` and the collector current is changed by 3 mA. the power gain in this circuit will be
View SolutionA message signal is used to modulated a carrier signal of frequency 5 MHz and peak side-bands are produced seperated by 40 kHz. If the modulation index is 0.75 then the peak voltage and frequency of the messages singal, respectively are
View Solution
PHYSICS questions and complete solutions for chapter TS EAMCET 2019 (6 MAY SHIFT 1) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12