Complete Solutions to All Questions of chapter PROPERTIES OF TRIANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | PROPERTIES OF TRIANGLES |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Take three non-collinear point `A ,\ B` and `C` on a page of your notebook. Join `A B ,\ B C` and `C A ,` what figure do you get? Name the triangle. Also, name The side opposite to `/_B` The angle opposite to side`\ A B` The vertex opposite to side `B C` The side opposite to vertex `Bdot`
View SolutionTake three collinear point `A ,\ B` and `C\ ` on a page of your note book. Join `A B ,\ B C` and `C Adot` is the figure a triangle? If not, why?
View SolutionDistinguish between a triangle and its triangle region.
View SolutionIn fig.9, `D` is a point on side `B C` of a `\ A B Cdot\ \ A D` is joined. Name all the triangle that you can observe in the figure. How many are they?
View SolutionIn fig. 10, `A , B , C` and `D` are four points, and no three points are collinear. `A C` and `B D` intersect at `Odot` there are eight triangle that you can observe. Name all the triangles.
View SolutionWhat is the difference between a triangle and triangular region?
View SolutionExplain the following terms: Triangle (ii) parts or elements of a triangle Scalene triangle (iv) isosceles triangle Equilateral triangle (vi) acute triangle Right triangle (viii) obtuse triangle Interior of a triangle (x) exterior of a triangle.
View SolutionIn fig. 11, the length (in cm) of each side has been indicated along the side. State for each triangle whether it is scalene, isosceles or equilateral:
View SolutionIn fig. 12, there are five triangles. The measures of some of their angles have been indicated. Sates for each triangle whether it is acute, right or obtuse.
View SolutionFill in the blanks with the correct word/symbol to make it a true statement: A triangle has........sides. A triangle has .......... vertices. A triangle has...........angles A triangle has.........parts. A triangle whose no two sides are equal is known as...... A triangle whose two sides are equal is known as......... A triangle whose all the sides are equal is known as...... A triangle whose one angle is a right angle is known as... A triangle whose all the angles are of measure less than `90^0` is known as....... A triangle whose one angle is more than `90^0\ ` is known as.......
View SolutionIn each of the following, state if the statement is true (T) or false (F). A triangle has three sides A triangle may have four vertices. Any three line-segment make up a triangle The interior of a triangle includes its vertices. The triangular region includes the vertices of the corresponding triangle. The vertices of a triangle are three collinear points. An equilateral triangle is scalene. Every right triangle is scalene. Each acute triangle is equilateral. No isosceles triangle is obtuse.
View SolutionTwo angles of a triangle are of measures `75^0\ a n d\ 35^0` find the measure of the third angle.
View SolutionOne of the angles of a triangle has measure `80^0` and the other two angles are equal. Find these two angles.
View SolutionOf the three angles of a triangle, one is twice the smallest and another is three times the smallest. Find the angles.
View SolutionEach of the two equal angles of a triangle is twice the third angle. Find the angles of the triangle.
View SolutionIf the angles of a triangle are in the ratio `2:\ 3:\ 4,` determine three angles.
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionOne of the acute angles of a right triangle is `58^0` , find the other acute angle.
View SolutionIn fig. `14 , A B C` is right-angled at `C ,\ a n d\ C D_|_A Bdot` also `/_A=65^0dot\ ` Find `/_A C D` (ii) `/_B C D` `/_C B Ddot`
View SolutionIn fig. `15 , D , E` are points on sides AB, AC of ` A B C` such that `D E||B Cdot` if `/_B=30^0\ a n d\ /_A=40^0,` find `x^0, y^0, z^0dot`
View SolutionThe fig.16 has been obtained by using two triangles. Find `/_A+/_B+/_C+/_D+/_E+/_Fdot`
View SolutionFig.17 is made up of two triangles. find `/_D A B+/_A B C+/_B C D+/_C D Adot`
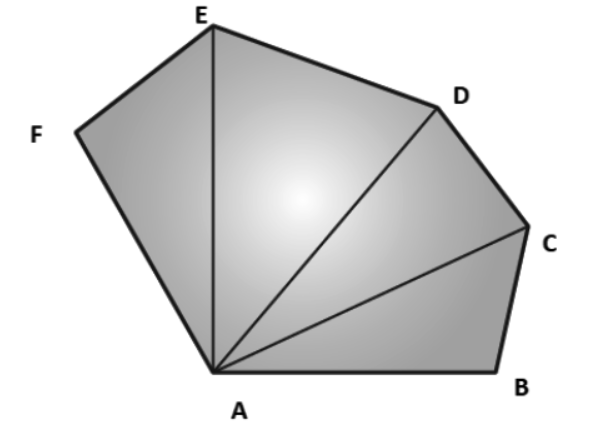
View SolutionIn five cornered fig. 18,`A D , A C` are joined. Find `/_E A B+/_B A C+/_B C D+/_C D E+/_D E A` .
View SolutionThe sides `A B` and `A C` of ` A B C` are product to `P` and `Q\ ` respectively. the bisectors of exterior angles at `B` and `C` of ` A B C` meet at `O\ ` (fig.19) prove that `/_B O C=90^0-1/2/_A`
View SolutionTwo angles of a triangle are of measures `105^0\ a n d\ 30^0dot` find the measures of the third angle.
View SolutionOne of the angles of a triangle is `130^0,` and the other two angles are equal. What is the measure of each of these equal angles?
View SolutionThe three angles of a triangle are equal to one another. What is the measure of each of the angles?
View SolutionIf the angles of a triangle are in the ratio `1:\ 2:\ 3,` determine three angles.
View SolutionThe angles of a triangle are `(x-40)^0,\ (x-20)^0\ a n d\ (1/2x-10)^0dot` find the value of `xdot`
View SolutionThe angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is `10^0,` find the three angles.
View SolutionTwo angles of a triangle are equal and the third angle is greater than each of those angles by `30^0` determine all the angles of the triangle.
View SolutionIf one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
View SolutionIf each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
View SolutionIn each of the following, the measures of three angles are given. State in which cases, the angles can possibly be those of a triangle: `63^0, 37^0, 80^0` (ii) `45^0, 61^0, 73^0` `59^0, 72^0, 61^0` (iv) `45^0, 45^0, 90^0` `30^0, 20^0, 125^0`
View SolutionThe angles of a triangle are in the ratio `3:4: 5.` Find the smallest angle.
View SolutionTwo acute angles of a right triangle are equal. Find the two angles.
View SolutionOne angle of a triangle is greater than the sun of the other two. What can you say about the measures of this angle? What type of a triangle is this?
View SolutionIn the six cornered figure, (fig.20), `AC,AD` and `AE` are joined. Find `/_F A B+/_A B C+/_B C D+/_C D E+/_D E F+/_E F Adot`
View SolutionFind `x , y , z` ( whichever is required) in the figures (fig.21) given below:
View SolutionIf one angle of a triangle is `60^0` and the other two angles are in the ratio `1:2,` find the angles.
View SolutionIf one angle of a triangle is `100^0` and the other angles are in the ratio `2:3,` find the angles.
View SolutionIn a ` A B C ,\ if\ 3/_\ \ A=4/_\ B=6/_\ C ,` calculate the angles.
View SolutionIs it possible to have triangle, in which Two of the angles are right? Two of the angles are obtuse? Two of the angles are acute? Each angle is less than `60^0?` Each angle is greater than `60^0?` Each angle is equal to `60^0?` Give reason in support of your answer in each case.
View SolutionIn ` A B C ,/_A=100^0` ,`A D\ b i s e c t s\ /_A\ a n d\ A D_|_B Cdotfin d\ /_Bdot`
View SolutionIn ` A B C ,/_A=50^0,/_B=70^0` and bisector of `/_C\ m e e t s\ A B\ in\ Ddot` find the angles of the triangle `A D C` and `B D Cdot`
View SolutionIn ` A B C ,` `/_A=60^0,\ /_B=80^0` and the bisectors of `/_B\ a n d\ /_C` meet at `O` . Find : (i) `/_C` (ii) `/_B O Cdot`
View SolutionThe bisectors of the acute angles of a right triangle meet at `O` . Find the angle at `O` between the two bisectors.
View SolutionIn ` A B C ,\ /_A=50^0\ a n d\ B C` is produced to a point D. The bisectors of `/_A B C\ a n d\ /_A C D` meet at `Edot` find `/_Edot`
View SolutionIn ` A B C ,\ /_B=60^0,/_C=40^0,\ A L_|_B C\ a n d\ A D` bisects `/_A` such that `L` and `D` lie on side `B Cdot` Find `/_L A Ddot`
View SolutionLine segments AB and CD intersect at O such that `A C||D B` . If `/_C A B=35^0` and `/_C D B=55^0` find the `/_B O Ddot`
View SolutionIn fig.22, ` A B C` is right angled at `Adot\ Q\ \ a n d\ R` are points on line `B C` and `P` is a point such that `Q P||A C` and `R P||A B` . Find `/_Pdot`
View SolutionIn fig.25,two of the angles are indicated what is the measure of`\ /_A C D ?`
View SolutionAn exterior angle of a triangle is `110^(0\ )\ ` and one of the interior opposite is `30^0\ ` find the other two angles of the triangle.
View SolutionOne of the angles of a triangle has measure `80^0` and the other two angles are equal. Find these two angles.
View SolutionIn fig.28, the measures of some of the angles are indicated. Find the values of `x^0` and `y^0`
View SolutionIn fig. 29, find `/_A B D ,` also, if `/_C=3\ /_A B C ,` find `/_A B Cdot`
View SolutionIn fig.30, find (i) `/_A C D ,` (ii) `/_A E D`
View SolutionThe sides `B C ,C A` and `A B` of a triangle `A B C ,` are produced in order, forming exterior angles `/_A C D ,/_B A E` and `/_C B F` . Show that `/_A C D+/_B A E+/_C B F=360^0`
View SolutionThe side `B C` of a`A B C` is produced on both sides. Show that the sum of the exterior angles so formed is greater than `/_A` by two right angles.
View SolutionSides `B C ,C A` and BA of a triangle `A B C` are produced to `D ,Q ,P` respectively as shown in Figure. If `/_A C D=100^0` and `/_Q A P=35^0,` find all the angles of the triangle. Figure
View SolutionIn Figure, the side `B C` of `A B C` is produced to form ray `B D` as shown. Ray `C E` is drawn parallel to `B A` . Show directly, without using the angle sum property of a triangle that `/_A C D=/_A+/_B` and deduced that `/_A+/_B+/_C=180^0dot`
View SolutionIn fig .35, `/_C B X` is an exterior angle of ` A B C` at `B` . Name The interior adjacent angle The interior opposite angles to exterior `/_C B X` Also, name the interior opposite angles to an exterior angle at `Adot`
View SolutionIn fig.36, two of the angles are indicated. What are the measures of `/_A C X\ a n d\ /_A C B ?`
View SolutionIn a triangle, an exterior angle at a vertex is `95^0` and it one of the interior opposite angles is `55^0` find all the angles of the triangle.
View SolutionOne of the exterior angles of a triangle is `80^0` , and the interior opposite angles are equal to each other. What is the measures of each of these two angles?
View SolutionThe exterior angles, obtained on producing the base of a triangle both ways are `140^0\ ` and `136^0` . Find all the angles of the triangle.
View SolutionThe sides `B C ,C A` and `A B` of a triangle `A B C ,` are produced in order, forming exterior angles `/_A C D ,/_B A E` and `/_C B F` . Show that `/_A C D+/_B A E+/_C B F=360^0`
View SolutionIn fig.38,`\ A C_|_C E\ a n d\ /_A :/_B :/_C=3:2:1,` find the value of `/_E C Ddot`
View SolutionA student when asked to measures two exterior angles of ` A B C` observed that the exterior angles at `A\ a n d\ B` are of `103^0\ a n d\ 74^0` respectively. Is this possible? Why or why not?
View SolutionIn fig.39, `A D\ a n d\ C F` are respectively perpendiculars to sides `B C\ a n d\ A B` of ` A B Cdot` if `/_F C D=50^0,\ fin d\ /_B A Ddot`
View SolutionIn fig.40, measures of some angles are indicted. Find the value of `xdot`
View SolutionIn fig.41, `A B C` is a right triangle right angled at `Adot\ D` lies on `B A` produced and `D E_|_B C ,` intersecting `A C` at `F` . if `/_A F E=130^0,` find `/_B D E` (ii) `/_B C A` `/_A B C`
View Solution`A B C` is a triangle in which `/_B=/_C` and ray `A X` bisects the exterior angle `D A C` . If `/_D A X=70^0` find `/_A C Bdot`
View SolutionThe sides BC of ` A B C` is product to a point `D` . The bisector of `/_A` meets side `B C` in `L` . If `/_A B C=30^0\ a n d\ /_A C D=115^0,` find `/_A L C`
View Solution`D` is a point on the side `B C` of ` A B Cdot` A line `P D Q` , though `D` , meets side `A C` in `P\ a n d\ A B` produced at `Q` . If `/_A=80^0,` `/_A B C=60^0` and `/_P D C=15^0` find (i) `/_A Q D` (ii) `/_A P Ddot`
View SolutionExplain in the concept of interior and exterior angles and in each of the figures given below. Find `x\ a n d\ y` (fig.42).
View SolutionCompute the value of `x` in each of the following figures.
View SolutionIn each of the following there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle: `2,3,4` (ii) `4,5,3` `2. 5 , 1.5 ,4`
View SolutionIn fig.45, ` A B C , A B=3c m , B C=4c m\ a n d\ A C=5c mdot` name the smallest and the largest angles of the triangle.
View SolutionIn each of the following, there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle: `5,7,9` (ii) `2, 10 , 15` `3,4,5` (iv) `2,5,7` `5,8, 20`
View SolutionIn fig.46, `P` is the point on the side `B Cdot` Complete each of the following statements using symbol `= , > or <` so as to make it true: `A P` .....`A B+B P` (ii) `A P` .....`A C+P C` `A P 1/2(A B+A C+B C)`
View Solution`P` is point in the interior of ` A B C` as shown in fig.47.states which of the following statements are true (T) or false (F): `A P+P B A C` `B P+P C=B C`
View Solution`O` is a point in the exterior of ` A B Cdot` what symbol ` > , <\ or\ =` will you use to complete the statement `O A+O BddotA B ?` write two other similar statements and show that `O A+O B+O C >1/2(A B+B C+C A)`
View SolutionIn ` A B C ,` `/_A=100^0,/_B=30^0,/_C=50^0dot` name the smallest and the largest sides of the triangle.
View SolutionThe hypotenuse of a right triangle is 13cm long. If one of the remaining two sides is of length 5cm, find the length of another side.
View SolutionThe sides of certain triangle are given below. Determine which of them are right triangle: a = 6 cm, b = 8cm and c = 10cm a = 5cm, b = 8cm and c = 11cm.
View SolutionA ladder is placed in such a way that its foot is at a distance of 5 m from a wall and its top reaches a window 12 m above the ground. Determine the length of the ladder.
View SolutionA ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
View SolutionA ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the some point, the ladder is turned to other side of the street to reach a window 12 m high. Find the width of the street.
View SolutionA man goes 10 m due east and than 24 m due north. Find the distance from the starting point.
View SolutionABC is an isosceles right triangle, right-angled at `C` . Prove that: `A B^2=2A C^2dot`
View SolutionIn a ` A B C ,\ A D_|_B C` and `A D^2=B DxxC Ddot` prove that ` A B C` is a right triangle.
View SolutionA tree broke at a point but did not separate. Its top touched the ground at a distance of 6 dm from its base. If the point where is broke be at a height 2.5 dm from the ground, what was the total height of the tree before it broke?
View SolutionState Pythagoras theorem and its converse.
View SolutionIn right ` triangle A B C ,` the lengths of the legs are given. Find the length of the hypotenuse.
(i)`a=6\ c m ,\ b=8\ c m\ ` (ii) `a=8\ c m ,\ b=15\ c m` (iii)`a=3\ c m ,\ b=4\ c m` (iv) `a=2\ c m ,\ b=1. 5\ c m`
View SolutionThe hypotenuse of a triangle is 2.5 cm. If one of the sides is 1.5 cm. find the length of the other side.
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is right-angled triangle.
View SolutionThe sides of certain triangles are given below. Determine which of them are right triangles. a = 7 cm, b = 24 cm and c= 25 cm a = 9 cm, b = 16 cm and c= 18cm
View SolutionTwo poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m. Find the distance between their tops.
View Solution
All Questions questions and complete solutions for chapter PROPERTIES OF TRIANGLES of RD SHARMA MATHS (HINGLISH) of Class 7