Complete Solutions to CONCEPT APPLICATION (Level 1) of chapter GEOMETRY of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | GEOMETRY |
| PEARSON IIT JEE FOUNDATION | CONCEPT APPLICATION (Level 1) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
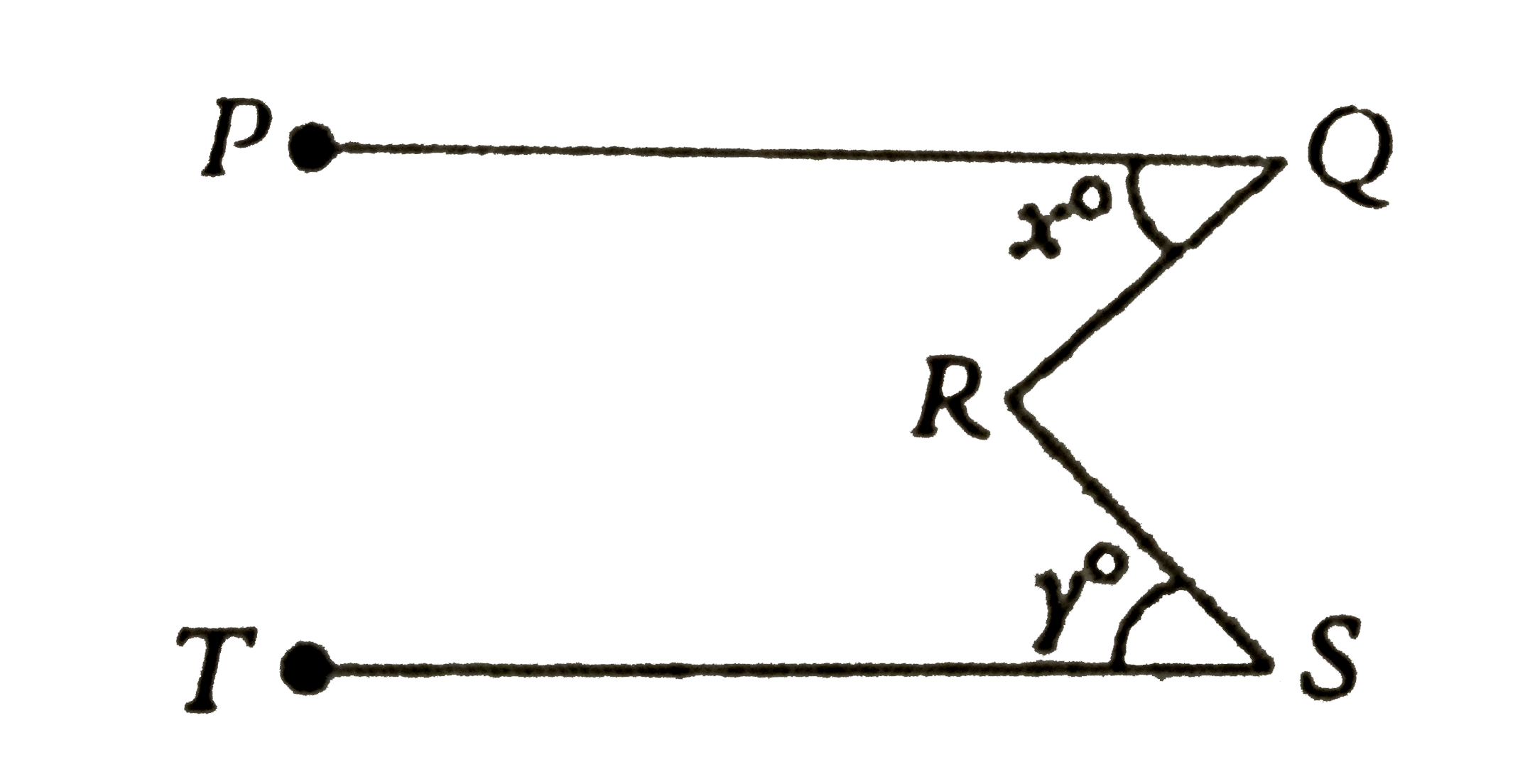
In the figure below (not to scale) , `bar(PQ)||bar(TS)`, reflex `/_ QRS=300^(@)` and `x-y =30^(@)`. The measure of `y` will be
View SolutionIn a triangle ABC, if `/_ A gt /_ B gt /_C` and the measures of `/_A , /_B ` and `/_ C` in degrees are integers, then the least possible value of `/_ A` is
View Solution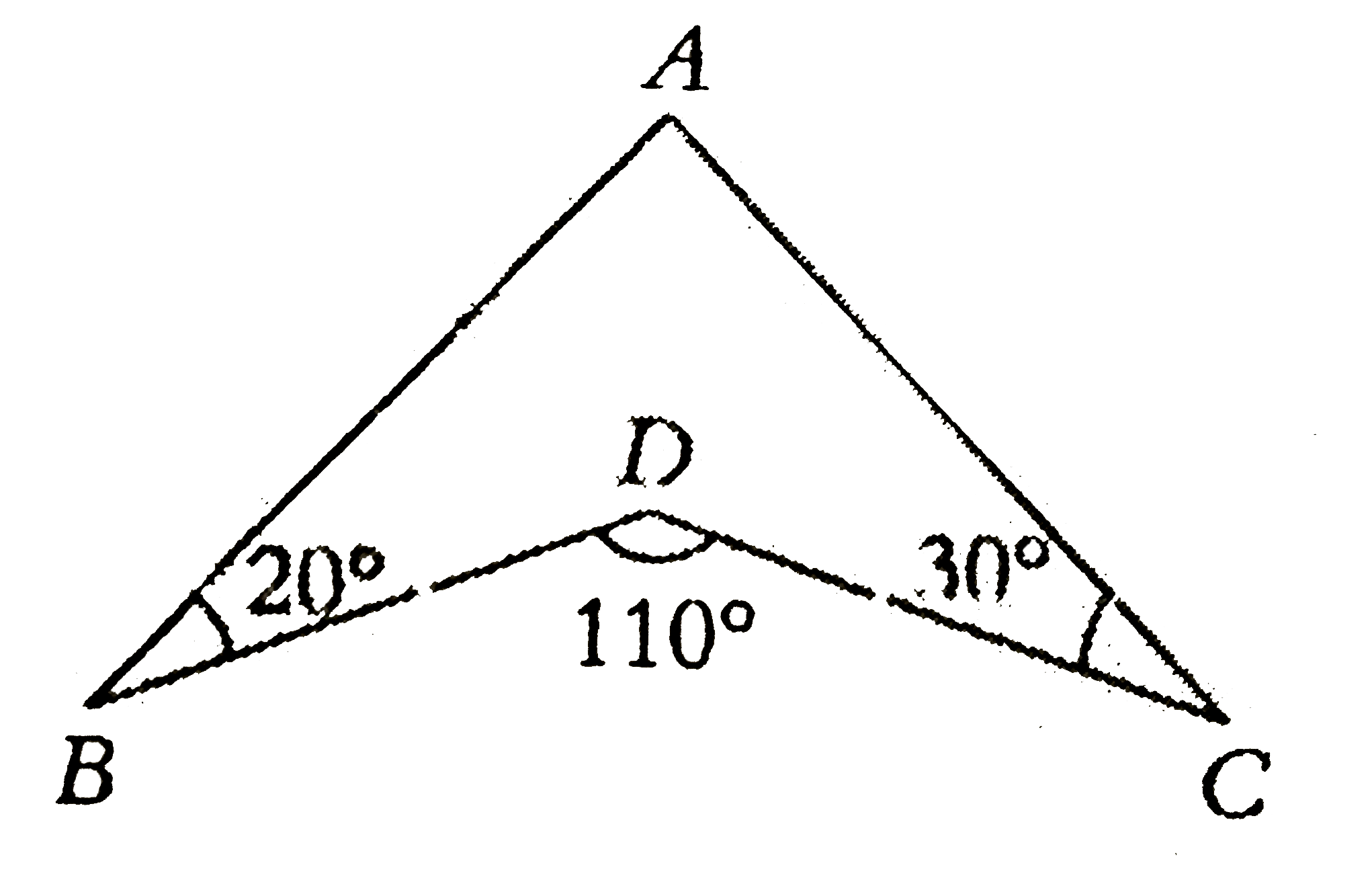
In the above figure, `/_ ABD =20^(@), /_ BDC =110^(@)` and `/_ DCA =30^(@)` . What is the value of `/_ BAC` ?
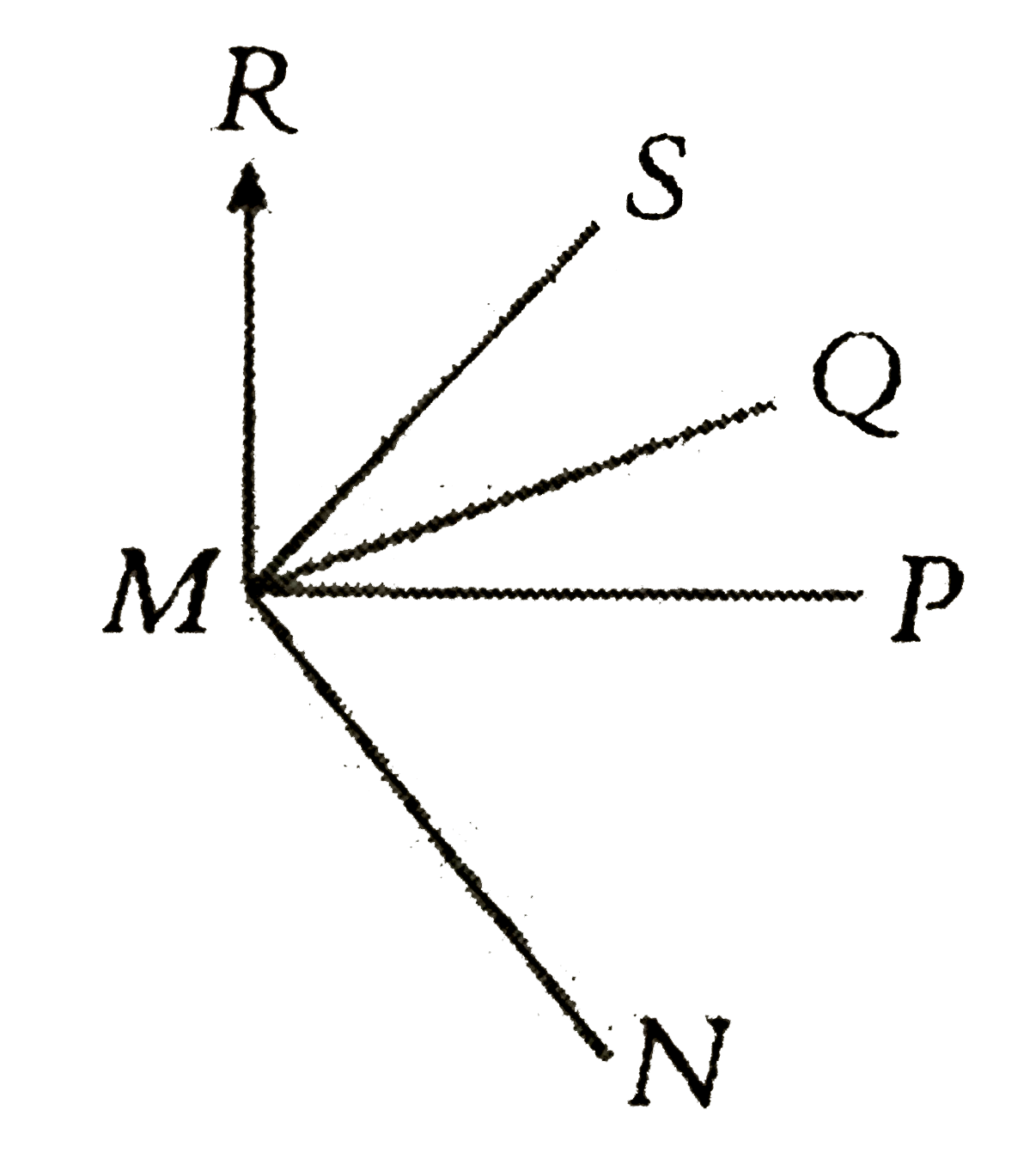
View SolutionIn the figure below (not to scale), `bar(MR )_|_ bar(MP), bar(MQ) _|_ bar(MN)`, and `bar(MS)` is bisector of `/_ RMQ` . If `/_ PMN=50^(@)` , then find the measure of `/_ RMS`.
View Solution
In the figure above (not to scale ) , `overline(EF)||overline(GD),overline(AF)||overline(EG),overline(AD)||overline(BC),andangleDCG=100^(@)`. if `angleCDG=40^(@)` , then find `angleAEF`.
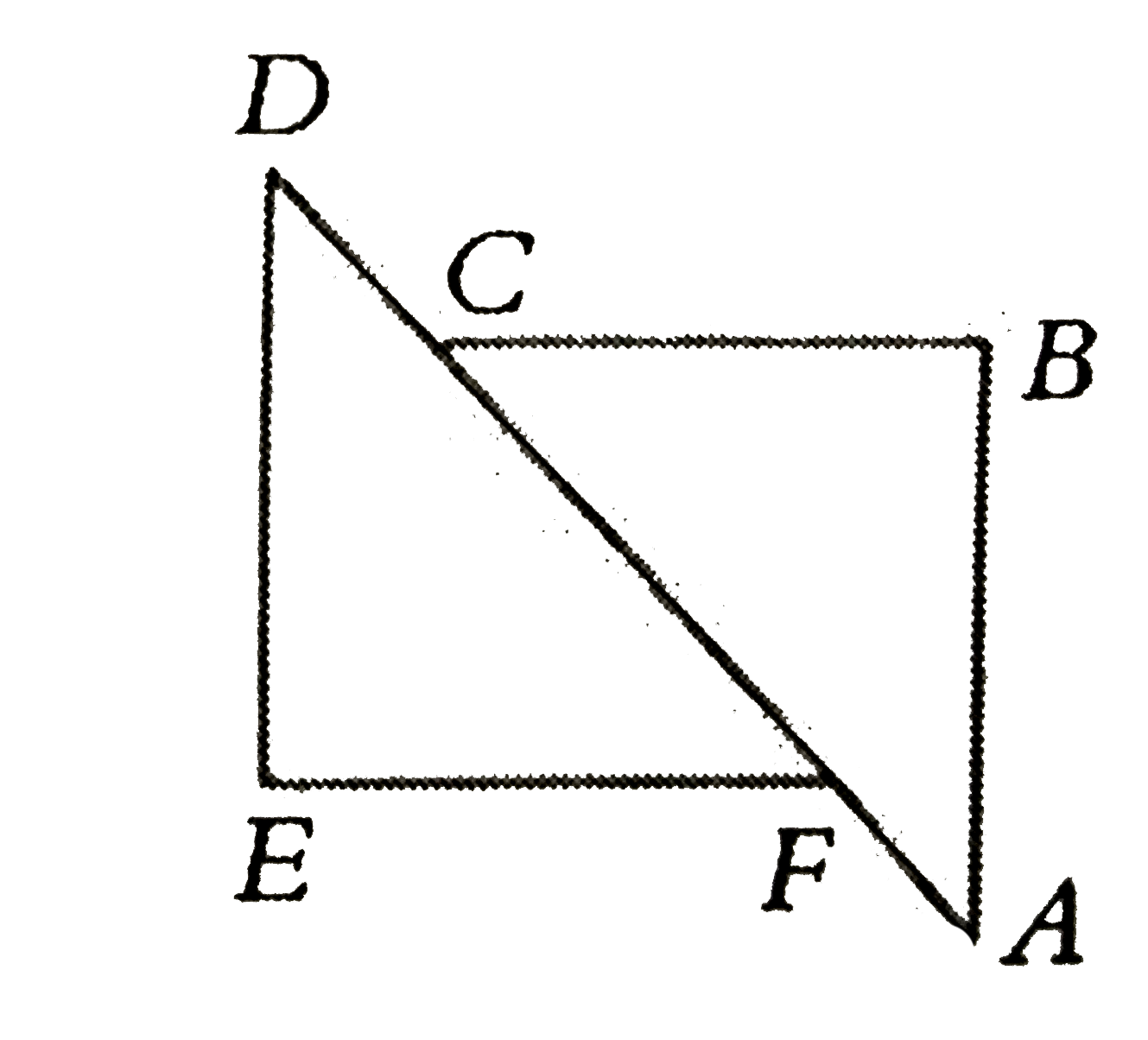
View SolutionIn the figure below, `bar(BC)|| bar(EF),BC=EF ` and `DF =AC`. Which of the following congurency axiom(s) is`//` are suitable to prove that `Delta BCA =Delta EFD` ?
View Solution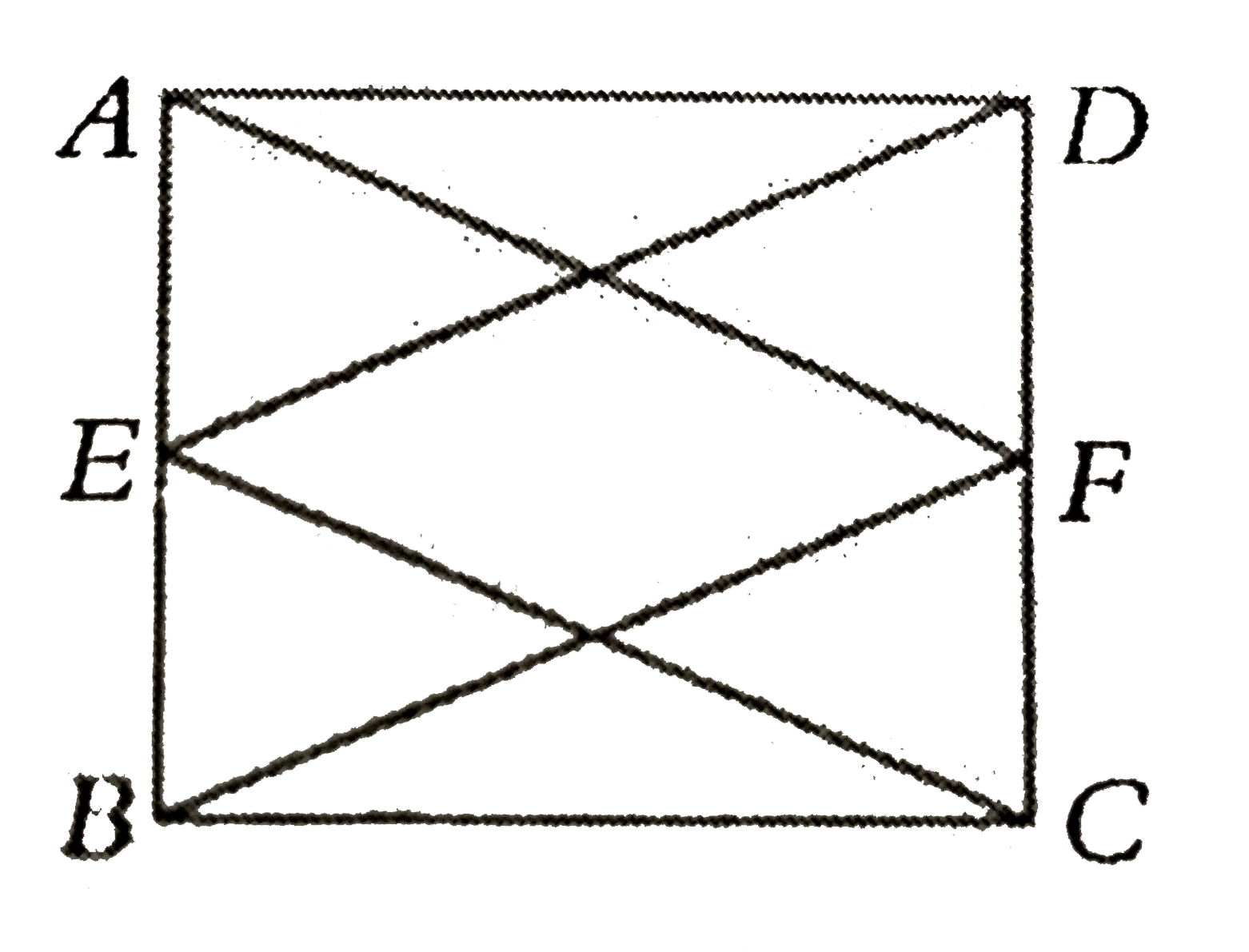
In the above figure (not to scale), E and F are the mid points of AB and CD respectively.
`bar(AB) | |bar(CD),bar(BC)||bar(AD),/_ADE =70^(@)`, AND `/_BCE =40^(@), /_DEC` is
View SolutionWhat is the number of lines of symmetry for a parallelogram ?
View SolutionGiven below are some figures. Choose the image of the given figure to have symmitrical image with respect to the given choices.

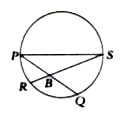
View SolutionIn the given figure , PQ and RS are chords of length 10 cm each intersecting at B . If `anglePBS=90^(@)and` the area of `DeltaPBS` is 32 `cm^(2)` , then the length of BR is ________ .
View Solution
In the above figure (not to scale), O is the centre of the circle. `bar(BC)` and `bar(CD)` are equal chords. If `/_ OBC =70^(@)` , then find `/_BAD`.
View Solution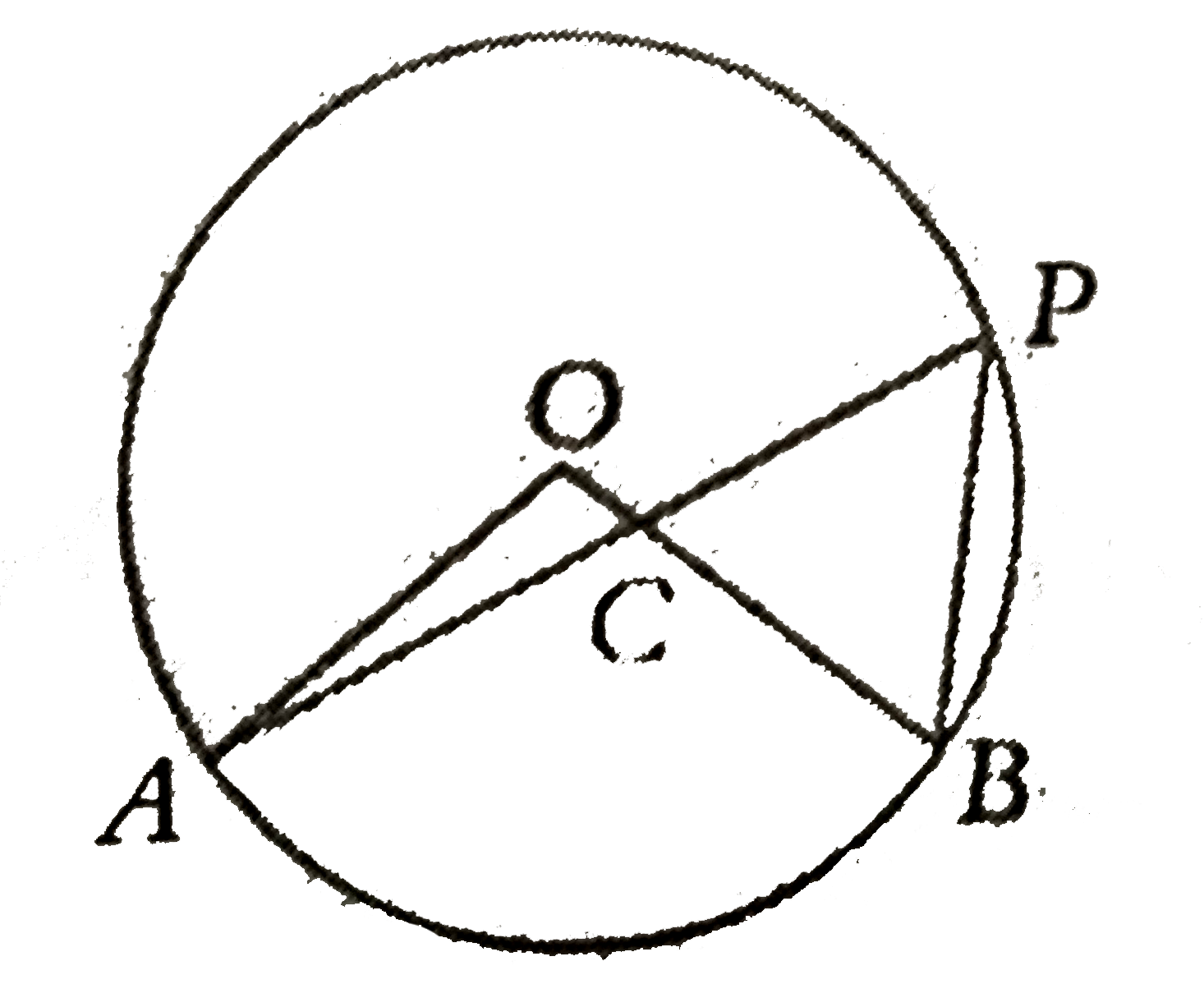
In the above figure (not to scale), O is the centre of the circle. `bar(AP)` and `bar(BP)` are two chords. C is the point of intersection of `bar(AP)` and `bar(OB)`. If `/_ OAC= 30^(@)` and `/_ PBC =80^(@)`, then `/_ AOB=`
View Solution
In the above figure , `overline(AB)andoverline(AC)` are equal chords and `overline(OD)` is perpendicular to `overline(AC)` . If `angleCOD=60^(@)`, then the angle between the chords is ______ .
View Solution
In the above figure, O is the centre of the circle and `AB=CD`. If `/_ APB=110^(@)`, then find the angle made by the chord CD at the centre.
View Solution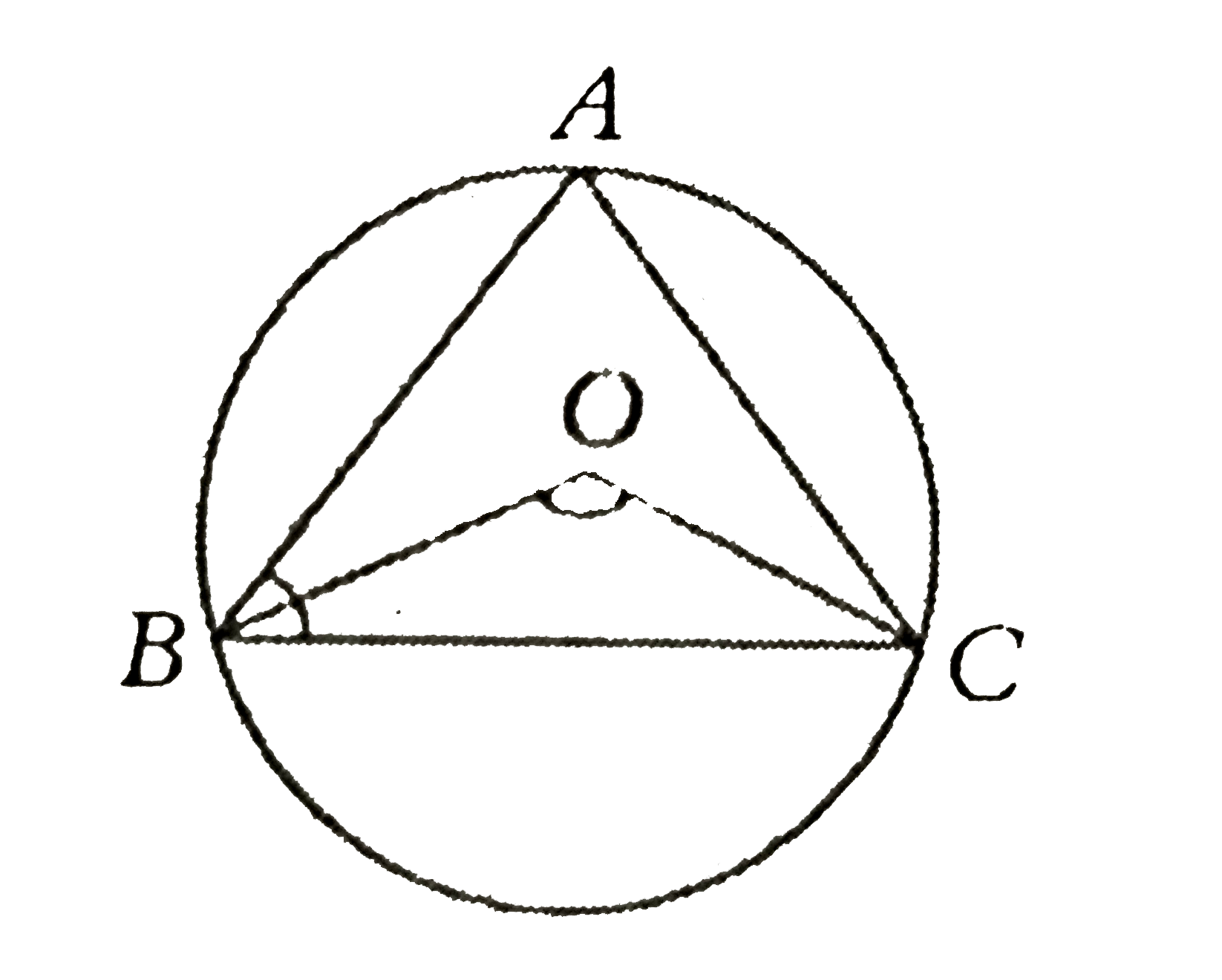
In the above diagram (not to scale), `AB=AC=`. O is the centre of the circle. If `/_ ABC =80^(@)`, then `/_ BOC =`
View Solution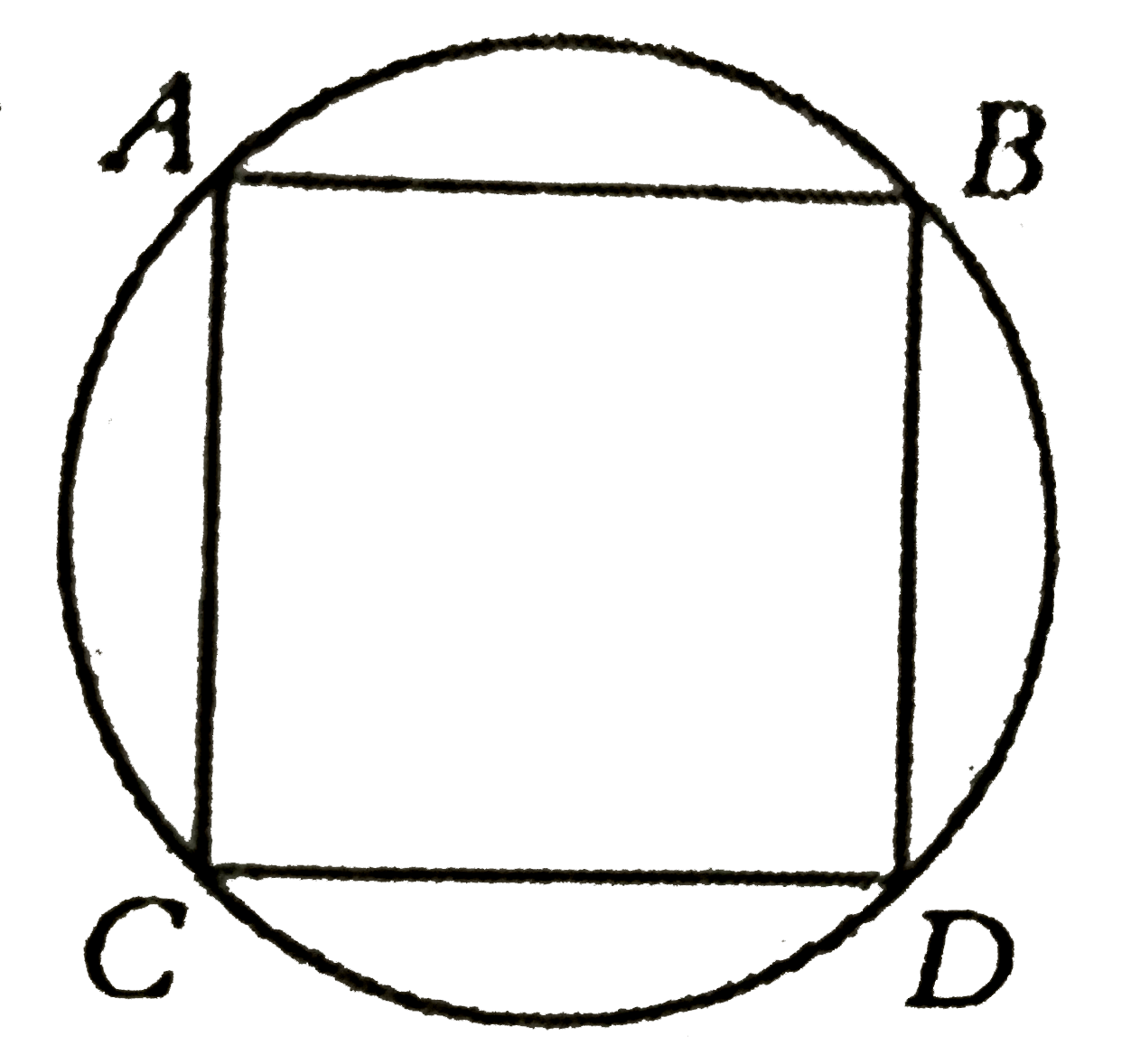
In the figure above (not to scale), `AB=CD` and `/_A =100^(@)`. `/_ C =`
View Solution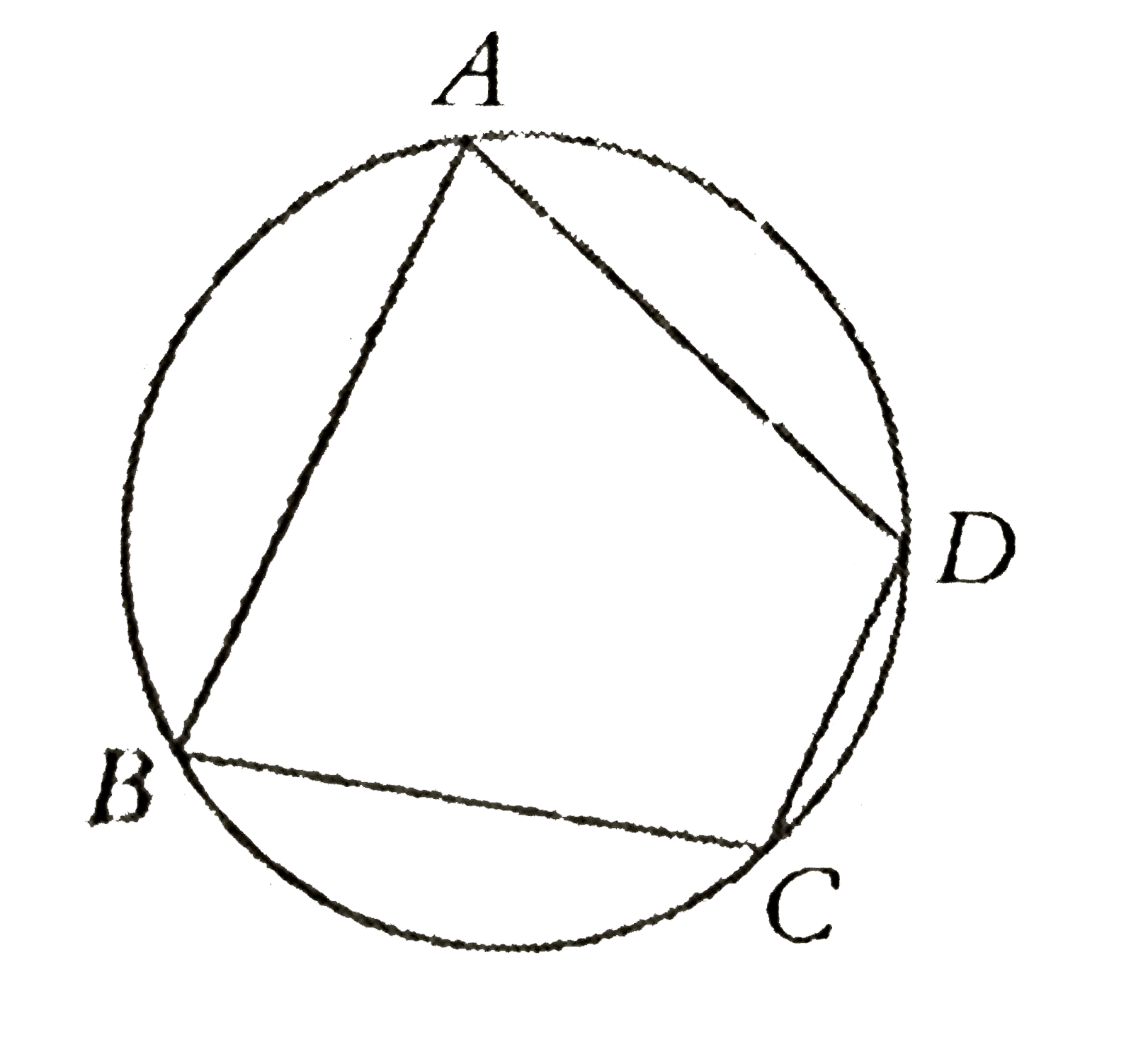
In the above figure, ABCD is a cyclic quadrilateral and `/_BCD =2 /_ BAD`. Find the angle made by the diagonal BD at the centre of the circle.
View SolutionIn the below figure , one part of the line of symmetry is given . Recognise the second part .

View Solution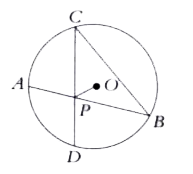
In the above figure , AB and CD are equal chords and O is the centre of the circle . If `angleOPB=50^(@)`, then `anglePBC=` ______ .
View Solution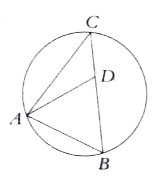
In the given figure , `angleDBA=2angleDAB=4angleCAD`. If `angleADC=120^(@)` , then the angle made by AB at the centre of the circle is _______.
View SolutionIn the given figure (not to scale ) , O is the centre of the circle . A ,B,C and D are conyclic and AB =CD . If `angleMON=120^(@)` , then find `angleOPN` .
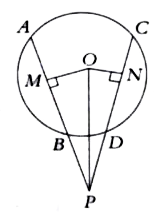
View SolutionIn the following figure ( not to scale), `/_ ADC =60^(@), /_ BAD =80^(@)` and `/_EBC = 2/_PDE`. Find `/_ APE`.
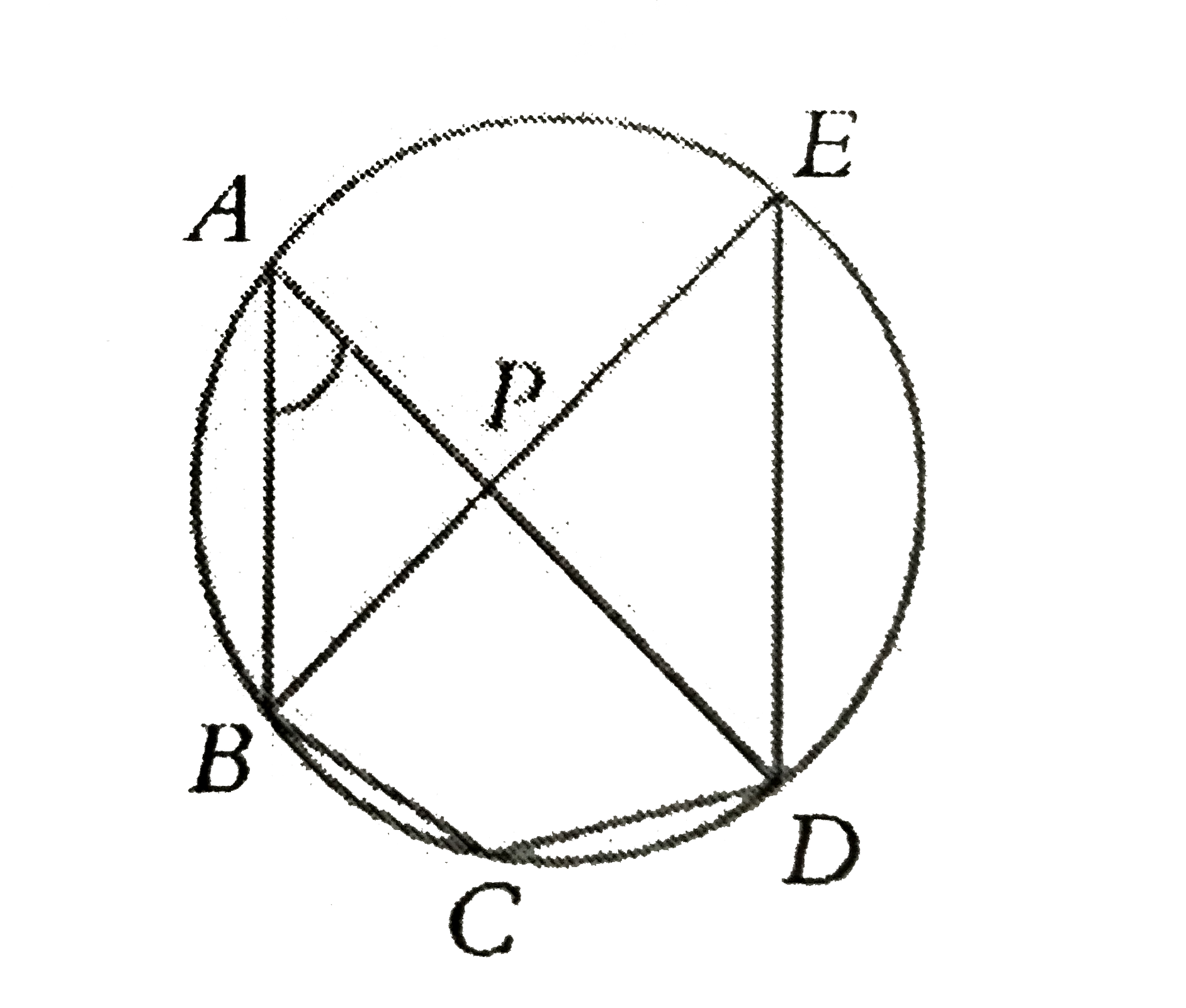
View SolutionIn the following figure , the two circles with centres P and Q are congruent.
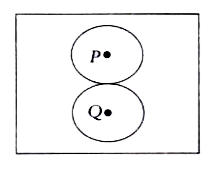
How many lines of symmetry does the above figure have ?
View Solution
In the above figure (not to scale) `overline(AB),overline(BC),overline(CF),overline(DE),andoverline(FE)` are chords of the circle . If `angleABC=100^(@)andangleFED=110^(@)` , then `angleFPA=` _______.
View SolutionIn the figure given below , `overline(ED)||overline(AB)andoverline(EF)||overline(BC)`. If `angleFED=40^(@)andangleDEC=20^(@)` , then the angle made by `overline(BC)` at the centre is _______.

View SolutionThe supplement of an angle and the complement of another have a sum equal to half of a complete angle. If the greater angle is `10^(@)` more than the smaller , find the smaller angle.
View SolutionABCD is a trapezium in which `AB ||CD, AB =20cm, BC =10` cm, `CD =10` cm and `AD =10` cm . Find `/_ADC`
View SolutionP is an interior point of quadrilateral ABCD and `AB =3.5`cm, `BC =4 cm, CD=4.8 cm ` and `AD =3.7 ` cm . Then which of the following can be the possible value of `(AP+BP+CP+DP)` ?
View SolutionIn the following figure (not to scale ), two chords XY and PQ are intersecting at the point A . The line segment joining X and P is a diameter of the circle , `angleXAP=120^(@)andXU=PQ=18cm` . Find the distance between the centre of the circle and the point A .
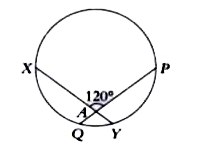
View SolutionThe angles of a triangle are in the ratio `2:3:4` . Find them
The following are the steps involved in solving the above problem.
Arrange them in sequential order from the first to the last.
(A) `2x+3x+4x=180^(@)`
`implies 9x= 180^(@)implies x=20^(@)`
(B) Let the angles be A,B and C. Given `A:B:C=2:3:4`
`implies A=2x,B=3x=C=4x`
(C ) We know that the sumf of the angles of a triangle is `180^(@), ie., A+B+C=180^(@)`
(D) The angles are `:A=2(20^(@))=40^(@),B=3(20^(@))= 60^(@)` and `C=4(20^(@))=80^(@)`.
View SolutionProve that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
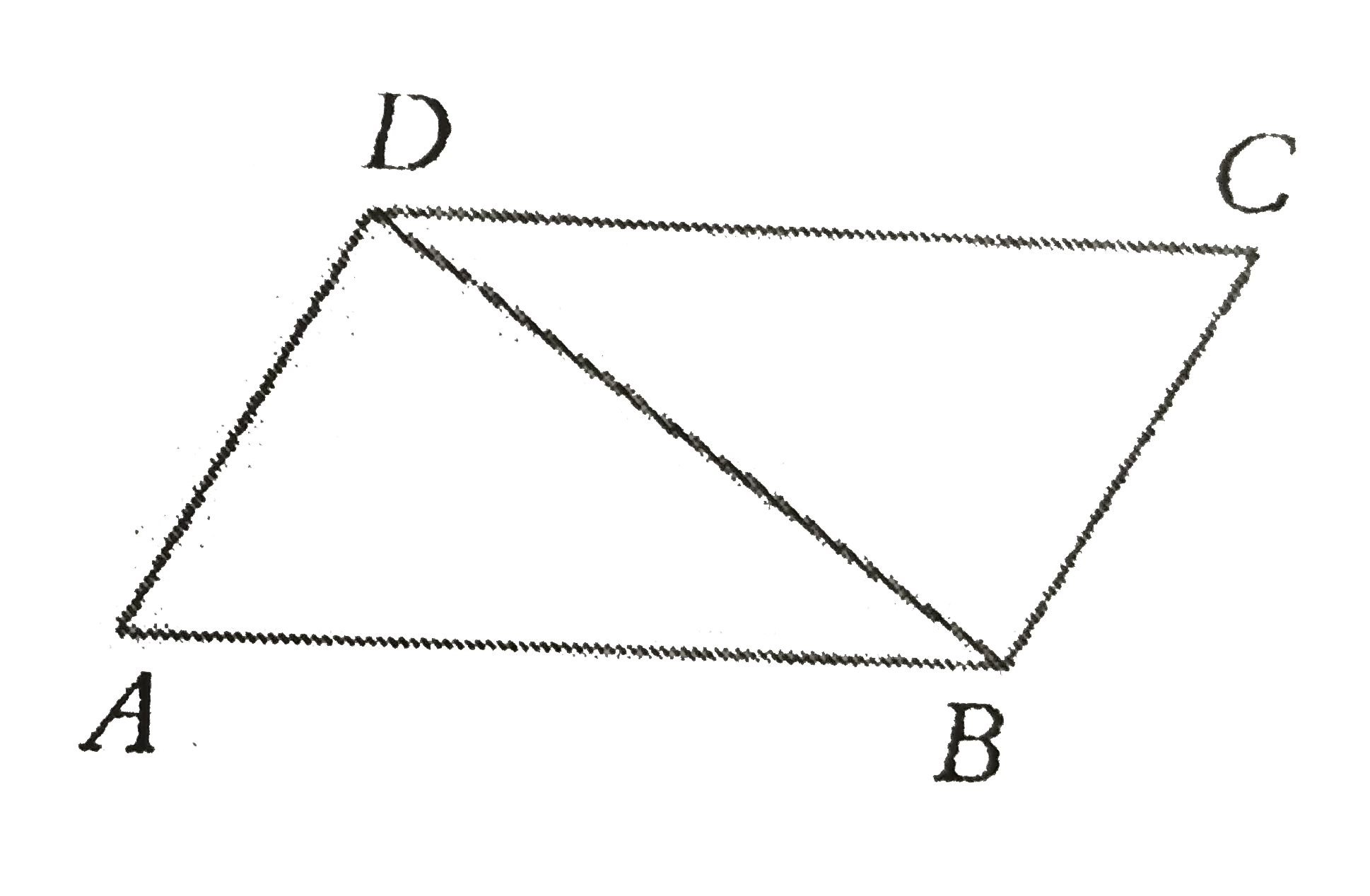
(A) By SSS conguruence property , `Delta DAB ~= Delta BCD`.
(B) Let ABCD be a parallelogram and join BD.
(C ) `AB=CD,AD=BC`(opposite sides of parallelogram) and `BD =BD` (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
View Solution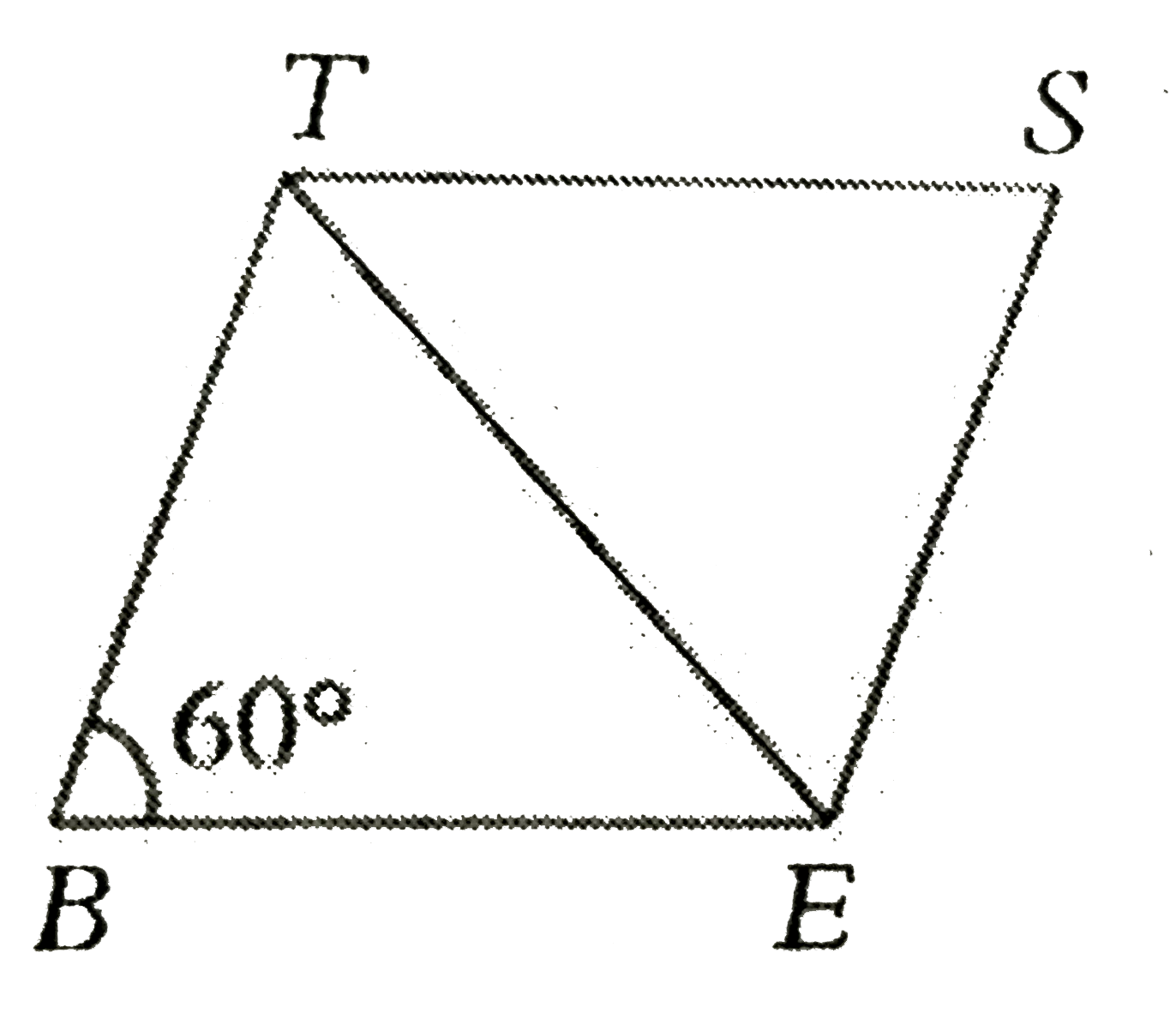
In a rhombus BEST,if `/_ B=60^(@)` and `BT =6cm`, then find the length of the diagonal TE.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) `implies Delta` BTE is an equilateral triangle.
(B) Join T and E
(C ) In `Delta BET, BT=BE implies /_ BTE =/_ BET =(180^(@)-60^(@))/(2)=60^(@) ( :' /_ B=60^(@))` .
(D) `TE=6 `cm
View SolutionThe following sentences are the steps involved in construction of the incircle for the triangle XYZ in which `/_Y =90^(@), XZ=6` cm and `YZ =4` cm.
Arrange them in sequential order from the first to the last.
(A) Mark the foot of the perpendicular from I onto YZ as D.
(B) Construct the triangle XYZ with `/_ Y =90^(@),XZ=6` cm and `YZ =4 cm`.
(C ) Draw a circle with I as the centre and ID as radius. This is the required incircle.
(D) Draw the bisectors of `/_ X, /_ Y` and `/_Z` and mark their point of concurrence as I.
View Solution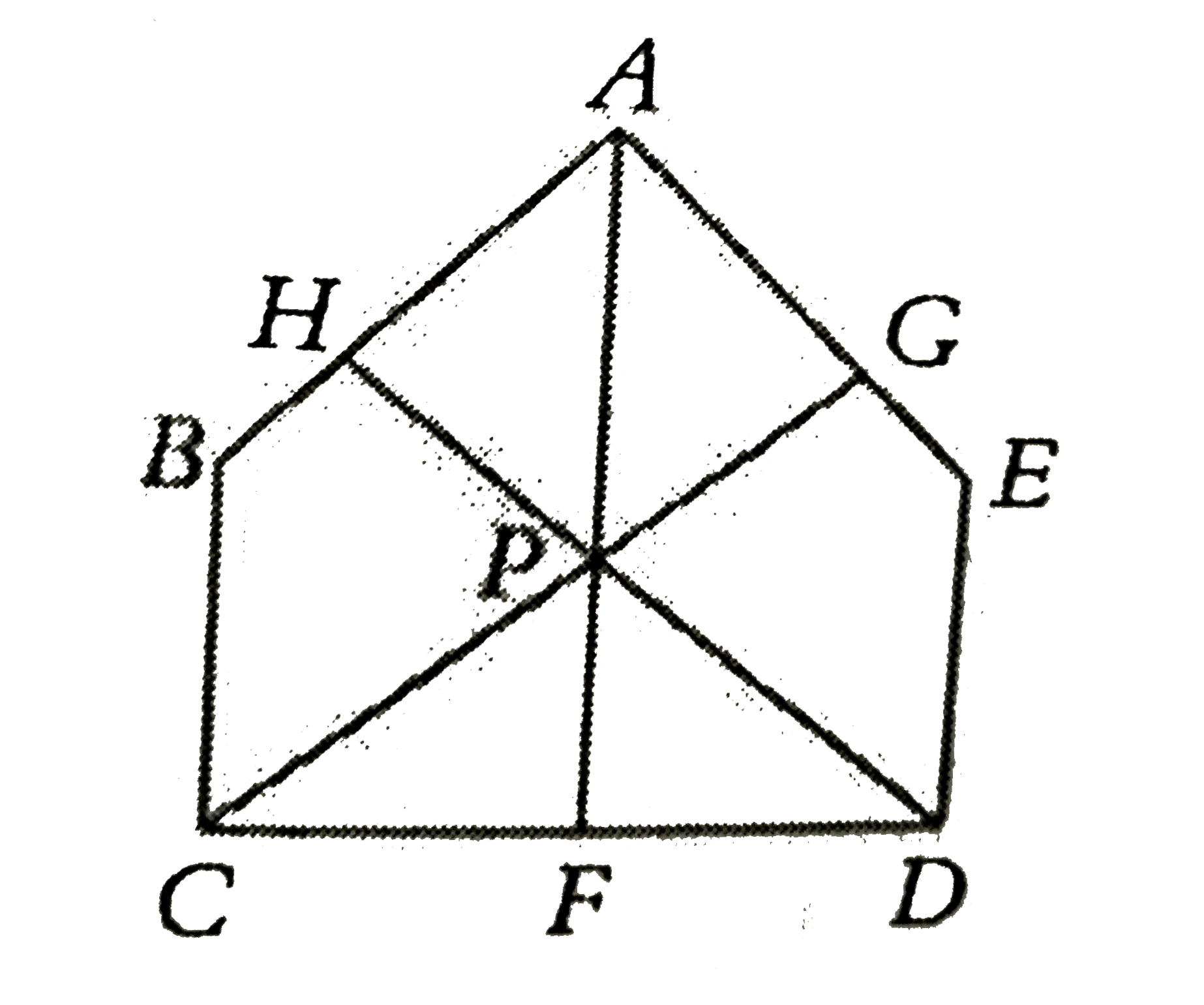
In the above figure, `bar(AF) || bar(ED),bar(CG) ||bar(AB)` and `bar(AE) ||bar(HD)` If `/_ FPD =40^(@)`, then `/_ AED =`
View Solution
In the above figure , DEF is a triangle whose side DF is produced to G .HF and HD are the bisectors of `angleEFGandangleEDG` , respectively . If `angleDEF=23(1)/(2)^(@)` , then `angleDHF` (in degrees) = _______.
View Solution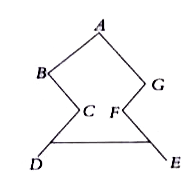
In the above figure ,`EF||AG,AB||CD||FG,andAG||BC`. If `angleEFG=70^(@)`, then `angleBAG-angleBCD=`_____.
View SolutionIn the figure below, `bar(AB)||bar(FC),bar(AE)||bar(BC)` and `bar(AF)||bar(BD)`. If `/_ F=x^(@),/_C = gamma^(@),/_EAB= k^(@)` and `/_ABD =p^(@)`, then which of the following options is correct ?
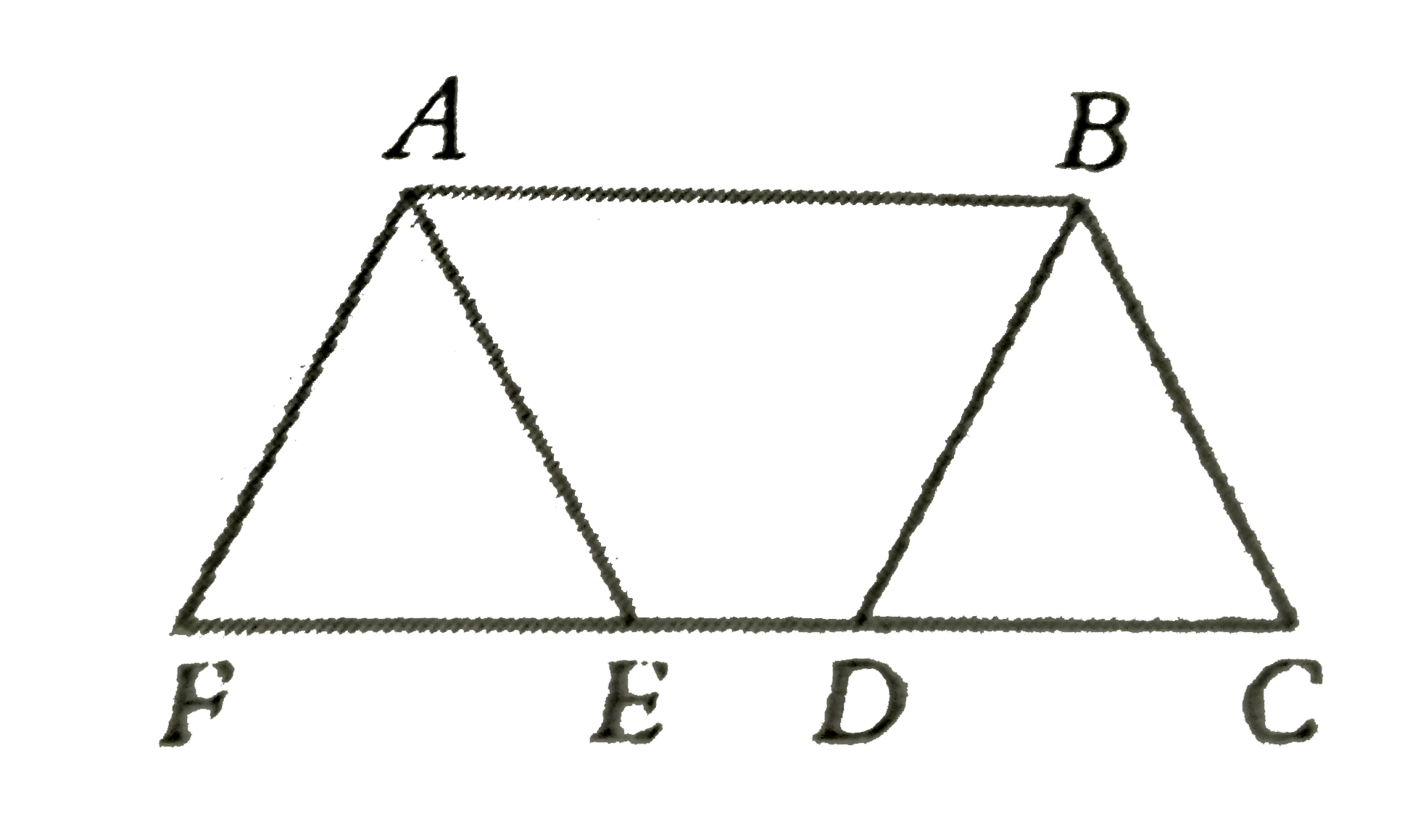
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
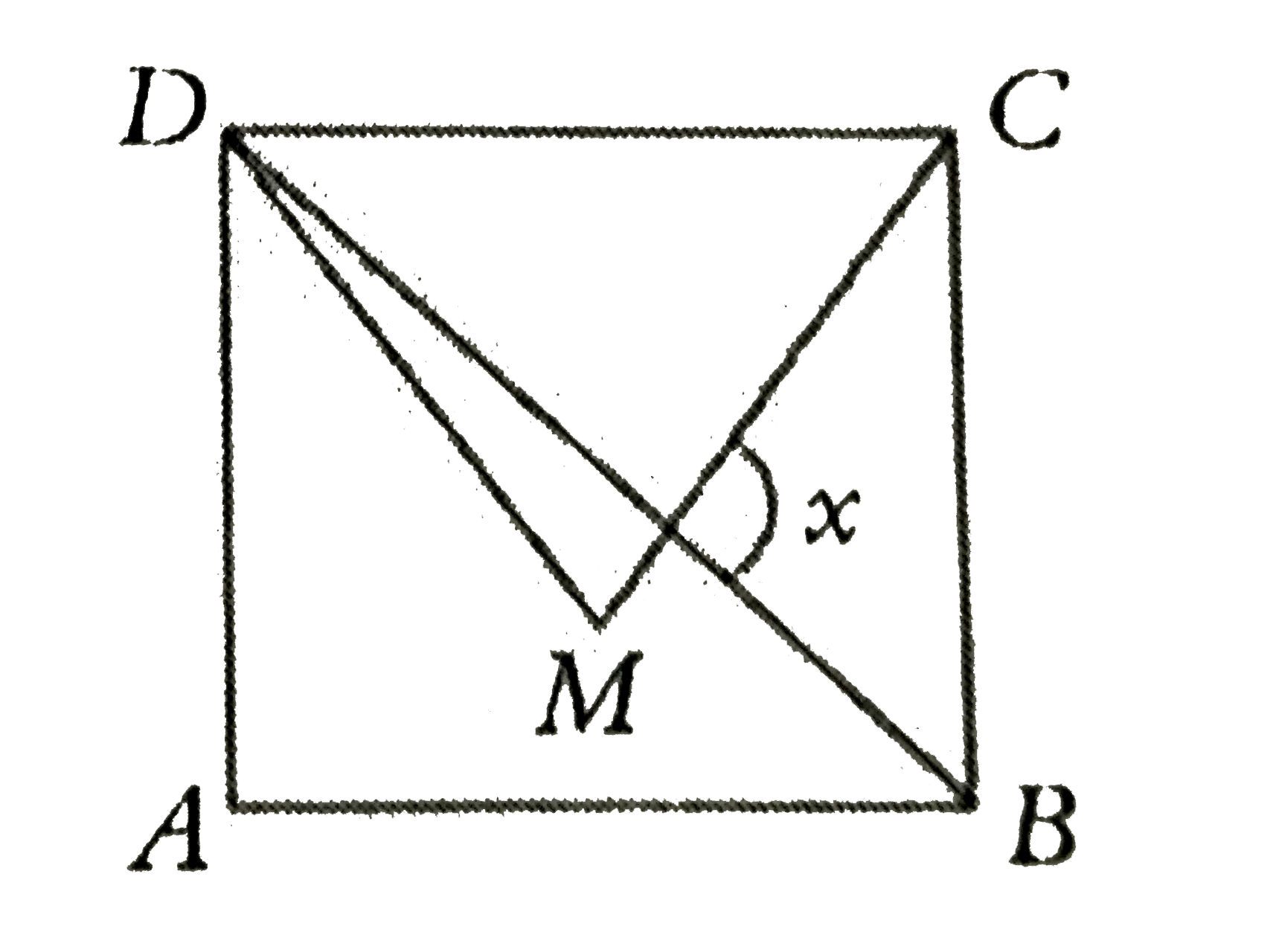
View Solution
In the above figure, `GH ||IJ` and `AC || BD, AB` and CD are bisectors of `/_ EAH` and `/_ FCJ` respectively. Find the `/_ ABD +/_ BDC `, if `/_ BAC= 3/_ BDC`.
View SolutionIn a mombus PORS,the diagonals intersect at o Given that `/_P=120^(@)` and `OP=3cm` .What is the side of the mombus?
View Solution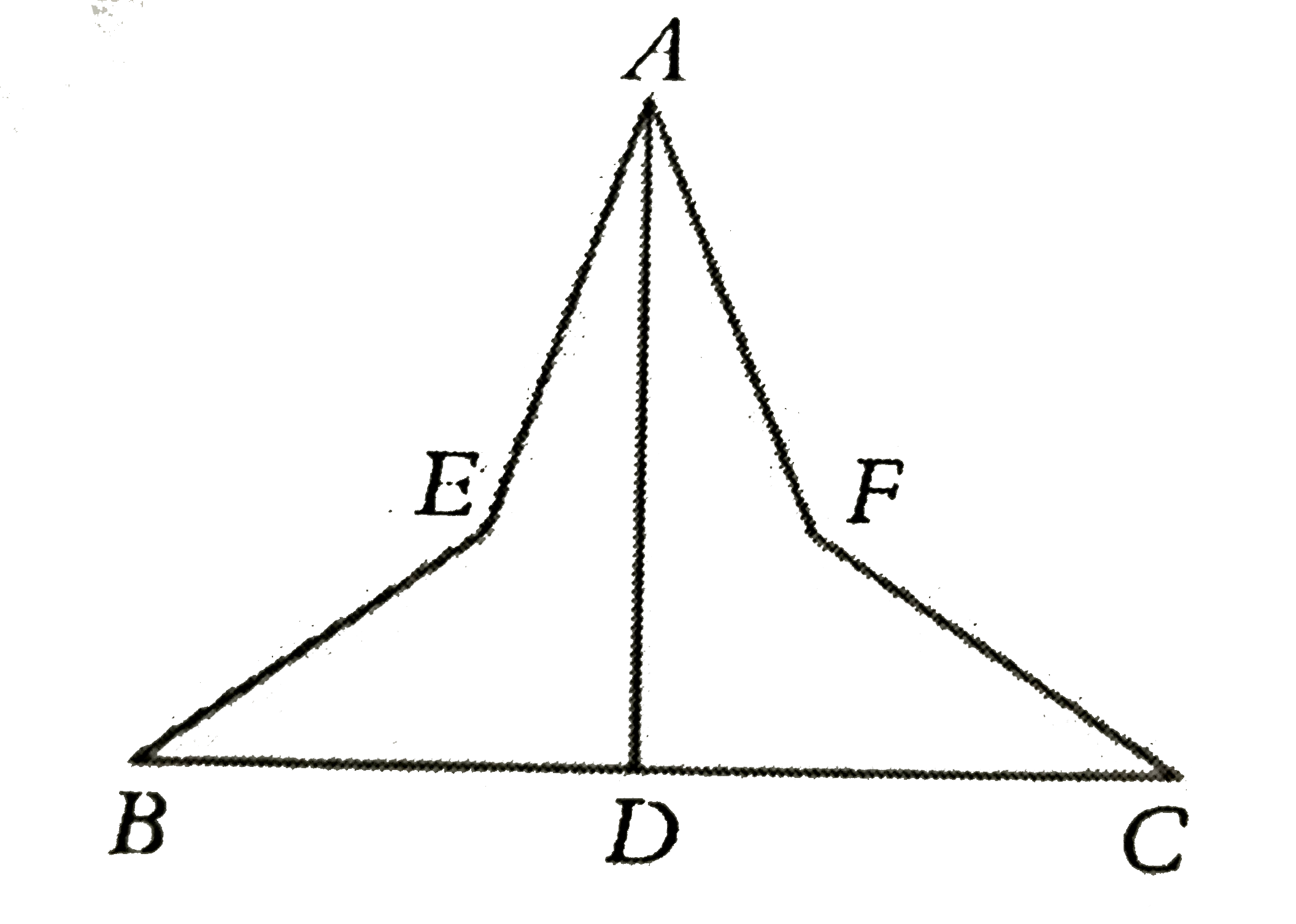
In the figuare above ( not to scale), `bar(AD)` is the angle bisector of `/_EAF, /_AFC = 110^(@)` and `/_ DCF =20^(@)`. If `/_ DAF =30^(@)` and `/_ EBD =10^(@)`, then `/_ AEB =`
View SolutionIn a rhombus ABCD, the diagonal intersect each other at O. If `/_ A =60^(@)` and `OA=2` cm, then the side of the rhombus is `"_______________"`
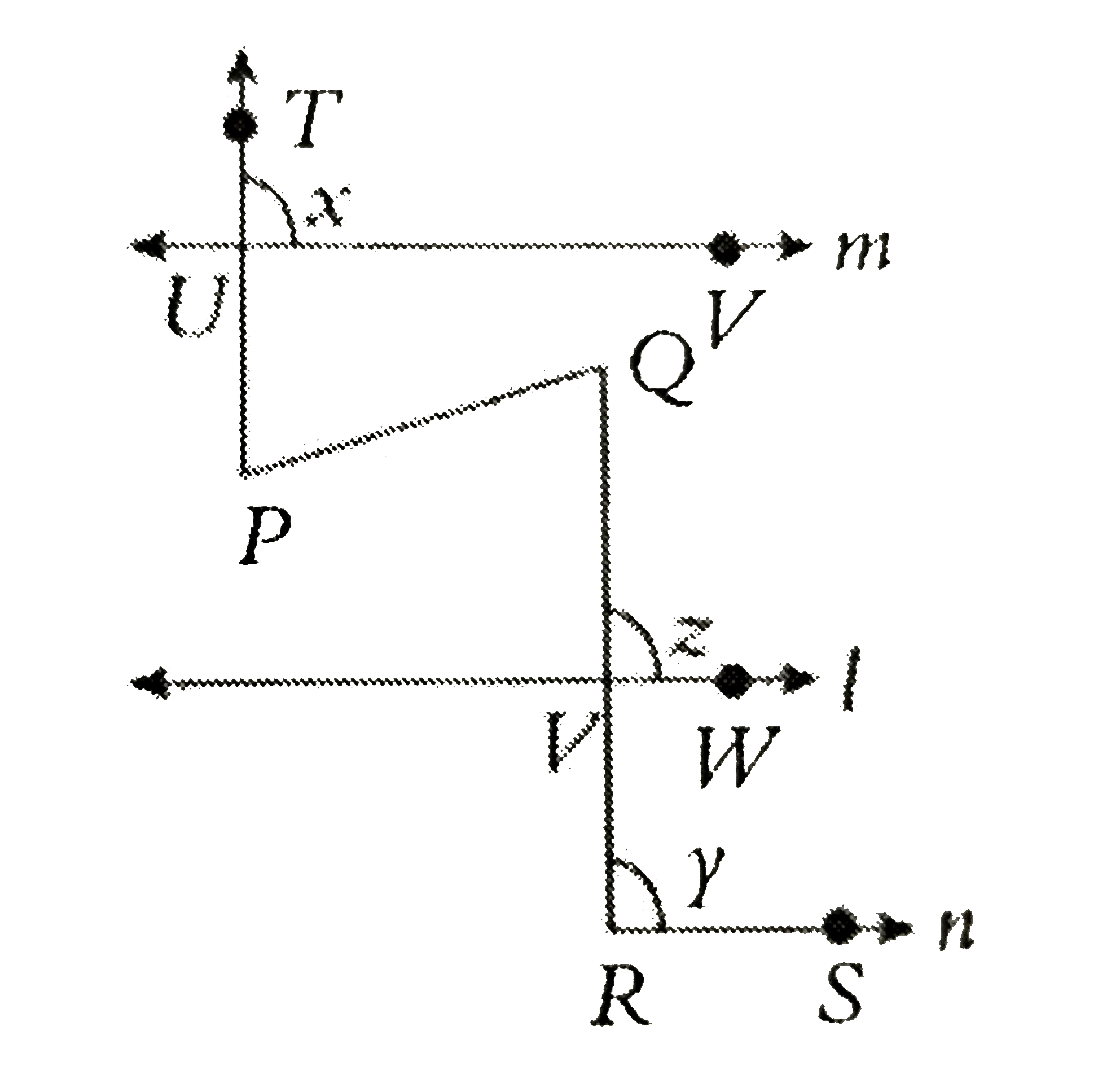
View SolutionIn the figure below, `m||l||n` and `bar(PT)||bar(QR)`. If `/_ TUV =x,/_QRS =gamma` and `/_ QVW =z`, then which of the following is necessarily true ?
View SolutionA circle is passing through three vertices of a rhombus of side 8 cm and its centre is the fourth vertex of the thombus .Find the length of the longest diagonal of the rhombus (in cm) .
View SolutionFind the sum of the interior angles of the polygon given below .
View Solution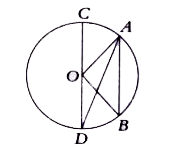
In the above figure (not to scale) , O is the centre of the circle and `overline(CD)||overline(AB)`.If `angleDAO=20^(@)` , then `angleAOB=` _______.
View Solution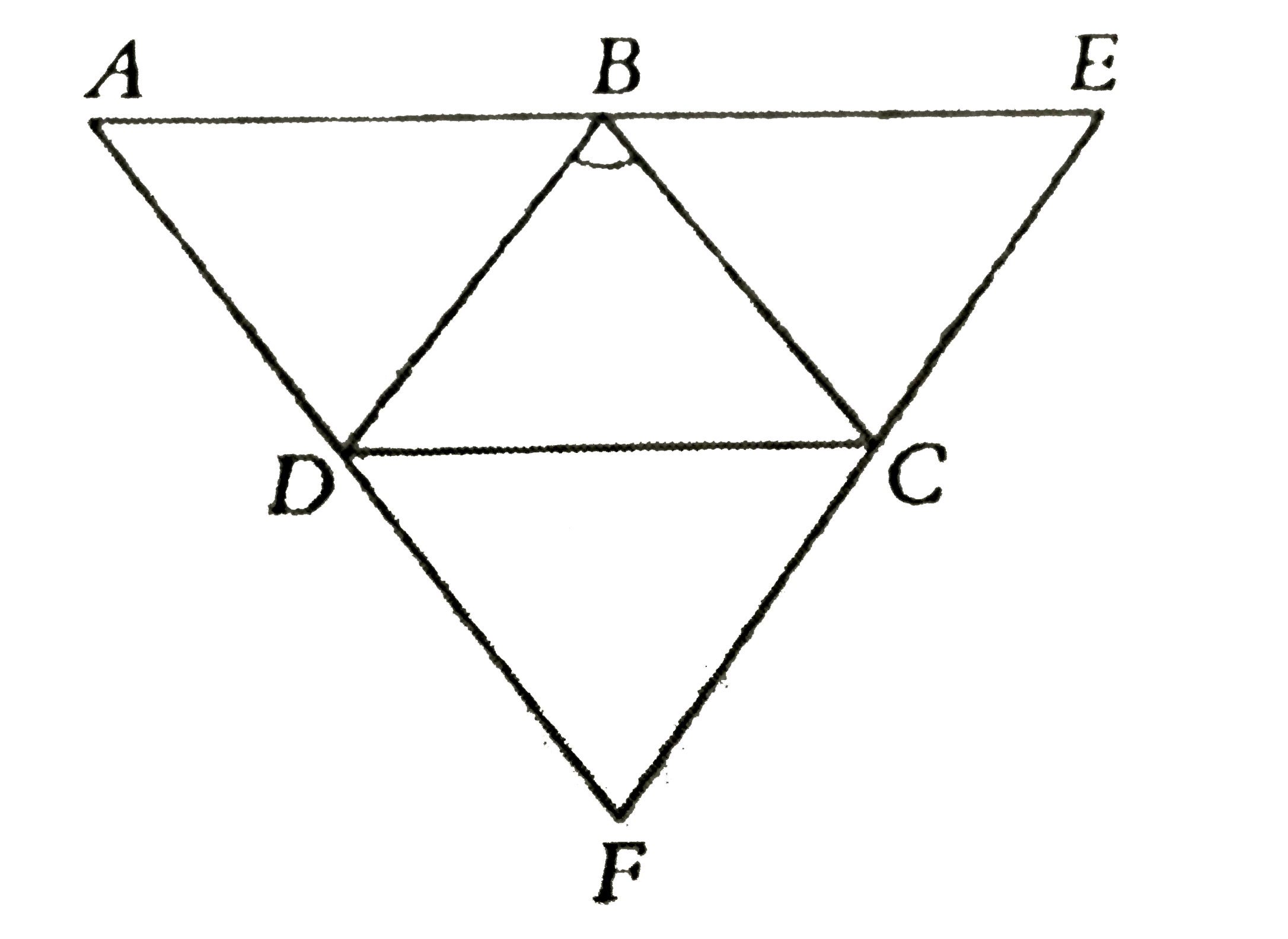
In the given figure, ABCD and BECD are parallelograms, BCFD is a rhombus. If `/_ DBC =80^(@), ` then which of the following are the angles of the triangle AEF ?
View SolutionThe perpenidicular drawn from the centre of a circle bisects any chord of the circle. The following are the steps involved in proving the above result. Arrange them in sequential order.
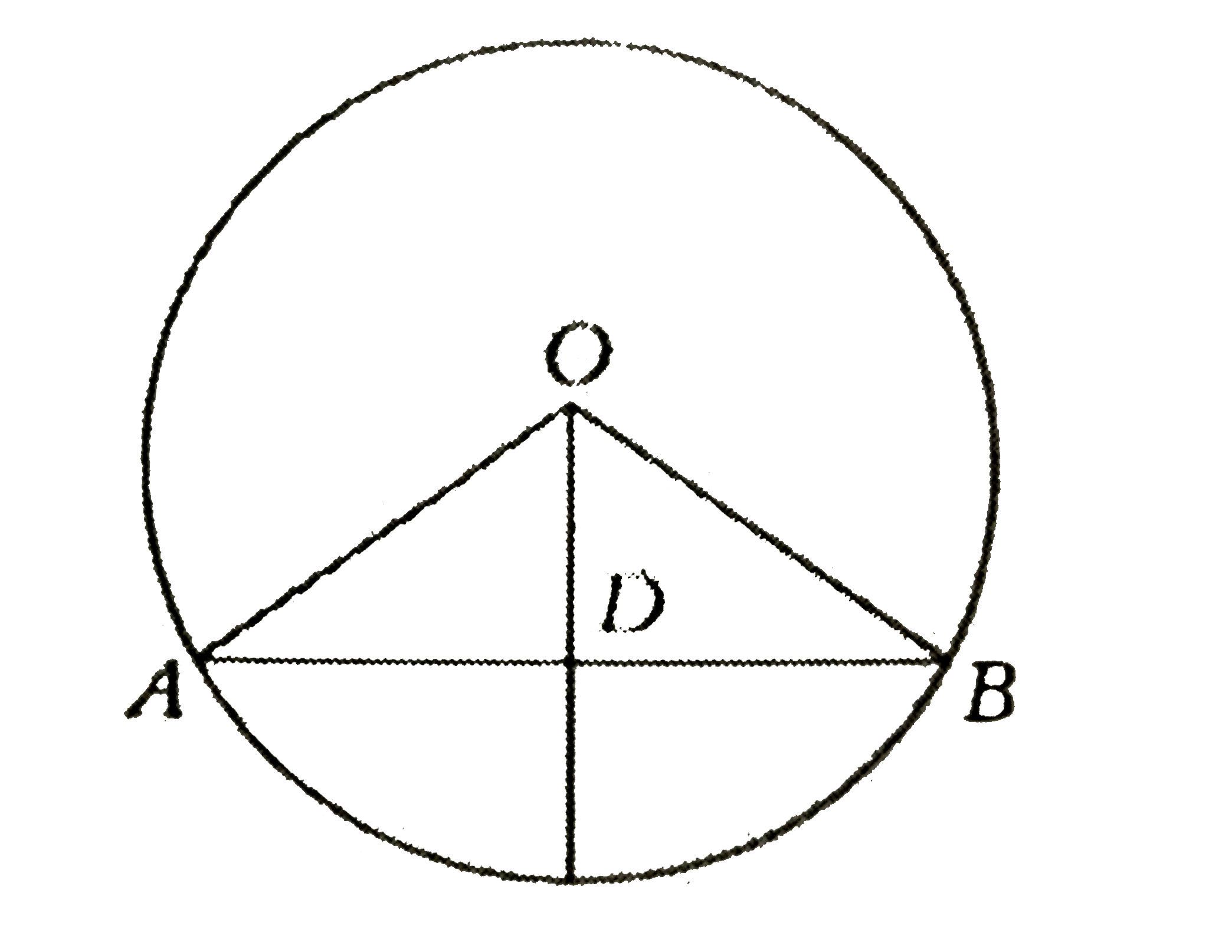
(A) Let `bar(OD) _|_ bar(AB)` .
(B) Let AB be the chord of the circle with centre O.
(C ) `Delta ODA -= Delta ODB` ( By RHS congruence property).
(D ) `OA =OB ` (radii), `OD= OD` ( common side) and `/_ ODA =/_ ODB =90^(@)`
(E ) `AD=DB` ( corresponding parts in congurents triangles ).
View SolutionIn the adjacent figure ( not to scale), O is the centre of the circle and `/_OBA =30^(@)`. Find `/_ ACB`.
The following sentences ae the steps involved in solving the above problem. Arrange them in sequential order from the first to the last.

(A) `/_OAB =30^(@), /_ OBA =30^(@)`
`implies /_ AOB =180^(@) -30^(@)-30^(@) =120^(@)`
(B) We known that `/_ ACD =("Reflex "/_AOB)/(2)=(240^(@))/(2)=120^(@)`
(C ) Reflex `/_ AOB =240^(@)`
(D ) `OA =OB` (radii) `implies /_ OBA= /_ OAB =30^(@)`.
View Solution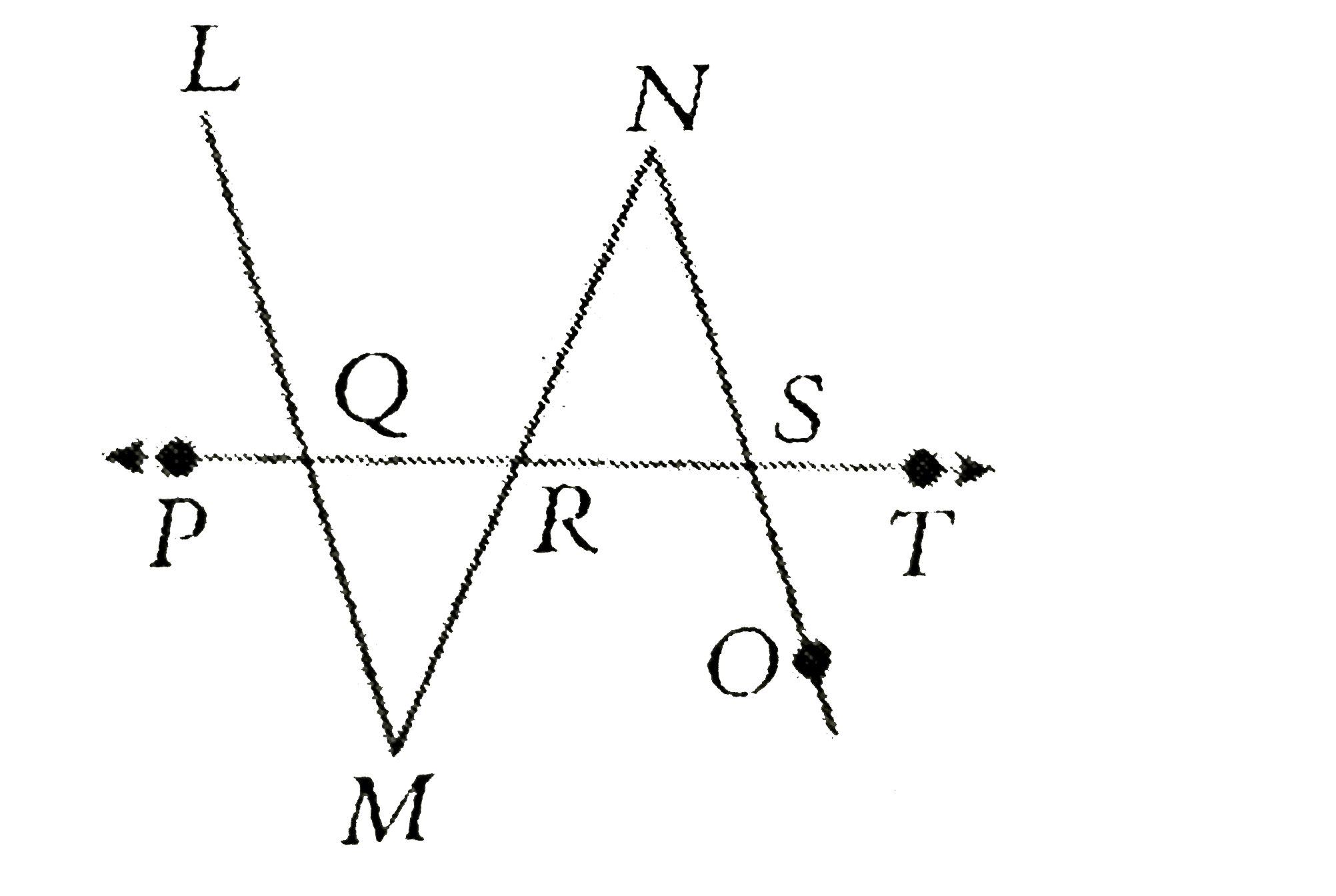
In the given figure , `bar(LM)||bar(NO), /_QMR=50^(@)` and `/_RSO =110^(@)`. Find `/_ MRQ`.
View Solution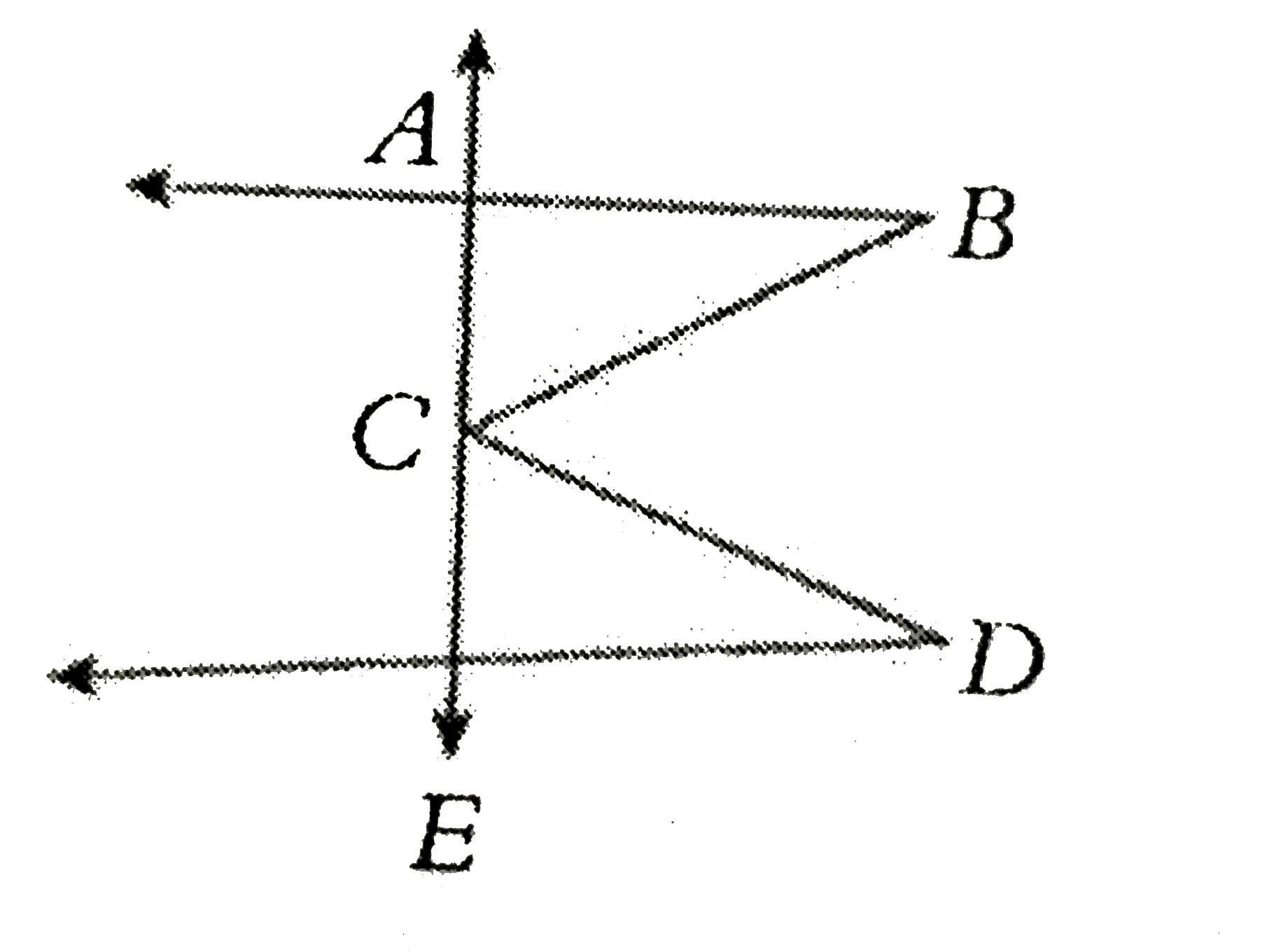
In the above figure, `bar(AB)||bar(DE)` and ACE is a straight line . I f `/_ABC =30^(@)` and `/_CDE =20^(@)`, then find `/_BCD`.
View Solution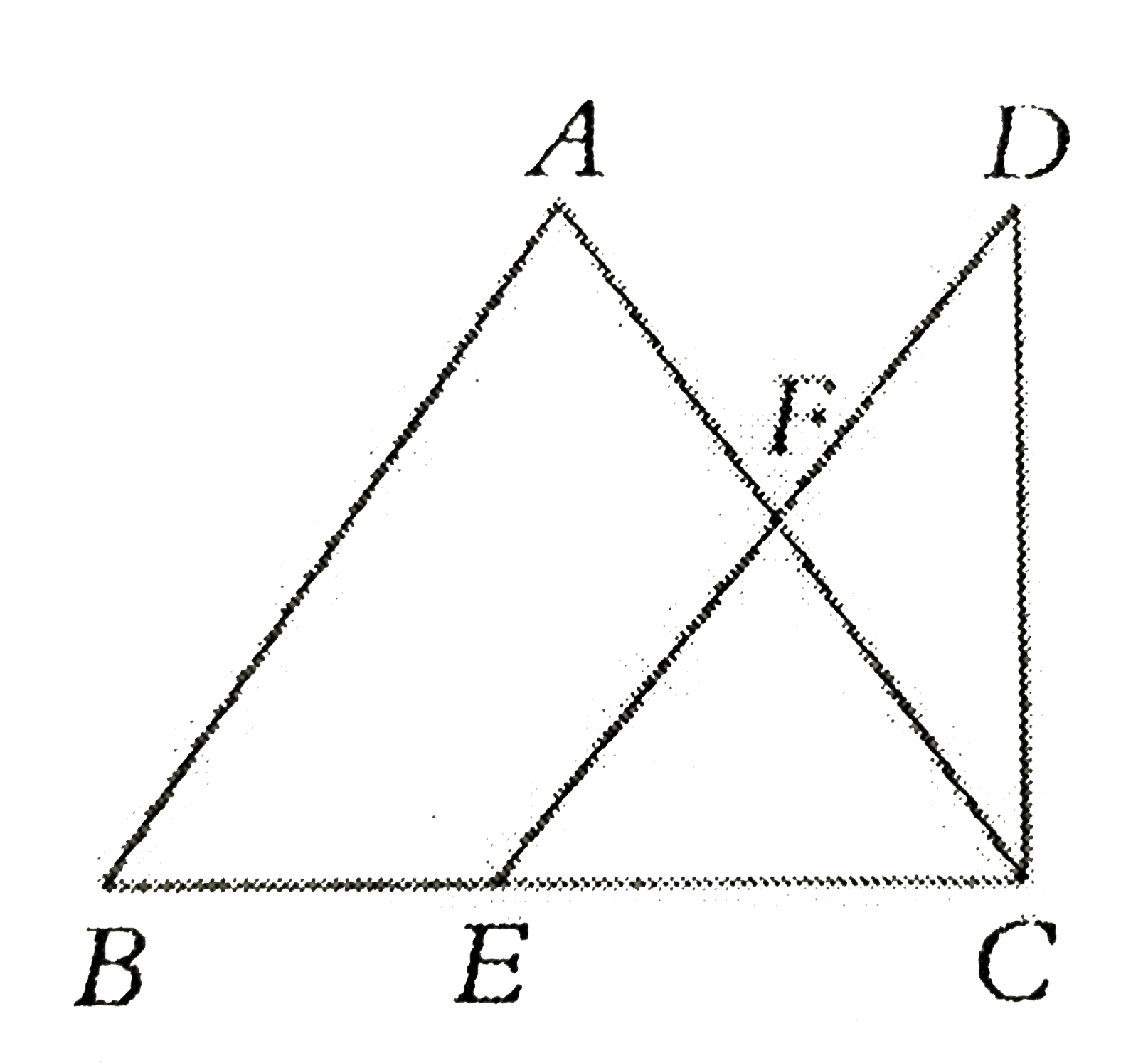
In the given figurs, `/_BAC =70^(@),/_BCD=80^(@),/_EFC =80^(@)` and `/_ABC =60^(@)`. How many isoscles triangles are there in the given figure ?
View Solution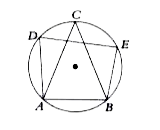
In the figure , A,B,C,andD are the points on the circle .If AB =BE and `angleACB=30^(@)` , then find `angleADE` .
View Solution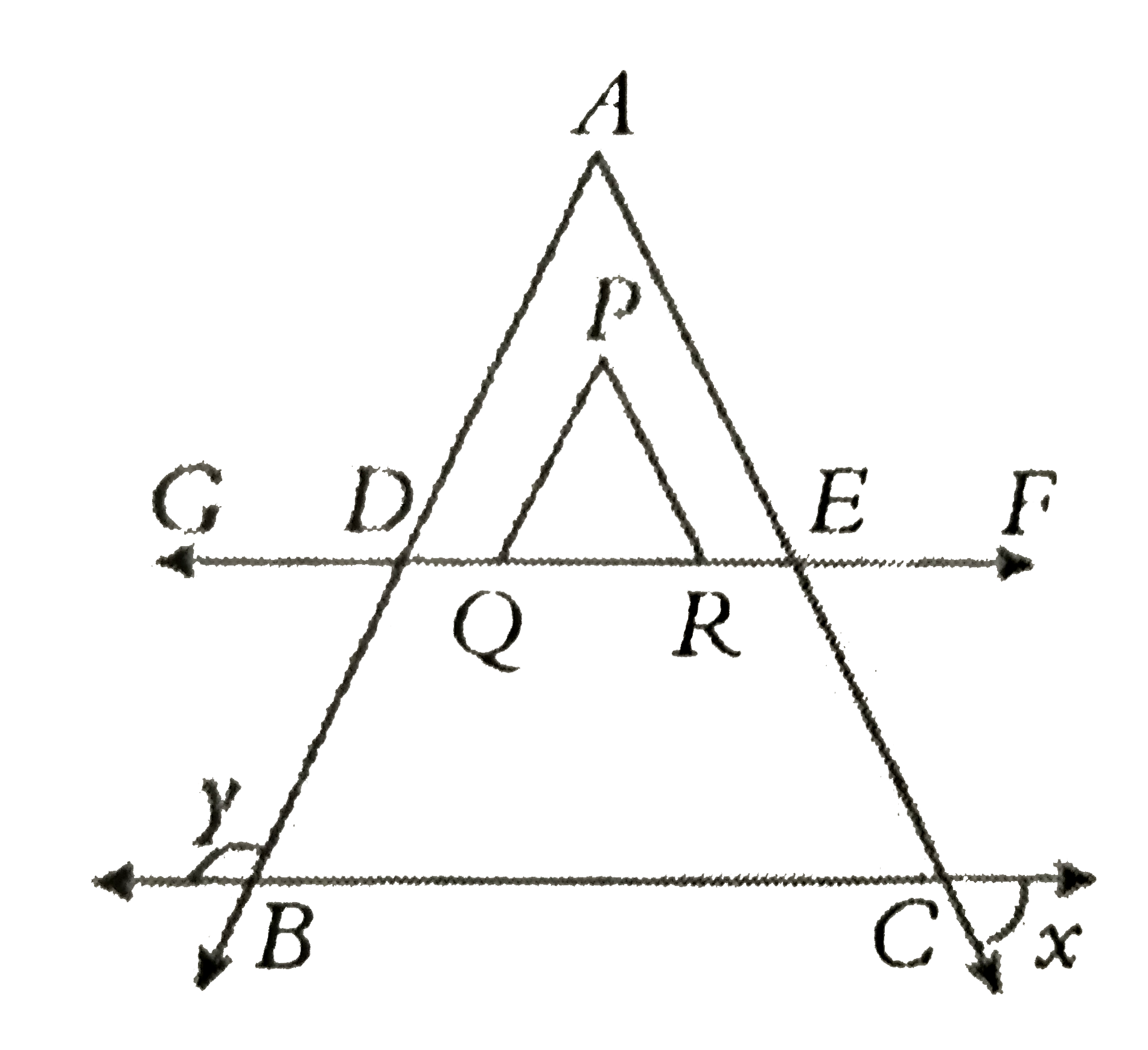
In the above figure (not to scale ), `bar(GF)||bar(BD),bar(B)||bar(PQ)` and `bar(AC)||bar(PR)` If `/_ x =40^(@)` and `/_ y= 110^(@)`, then find `/_ QPR`.
View Solution
In the figure above (not to scale ) , `angleABE=angleECDandangleEBD=angleACE`.If `angleBAC=80^(@)andangleBEC=100^(@)` , then `angleBDC`= _______.
View SolutionIn `Delta PQR, PD_|_ QR` and PO is the bisector of `/_ QPR`. If `/_ PQR=65^(@)` and `/_ PRQ =23(1)/(2). ^(@)` then `/_ DPO` in degrees `=`
View SolutionIn a parallelogram PQRS, the bisectors of `/_P` and `/_Q` meet on RS.If the perimeter PQRS is 13.5 cm, then find the measure of QR
View Solution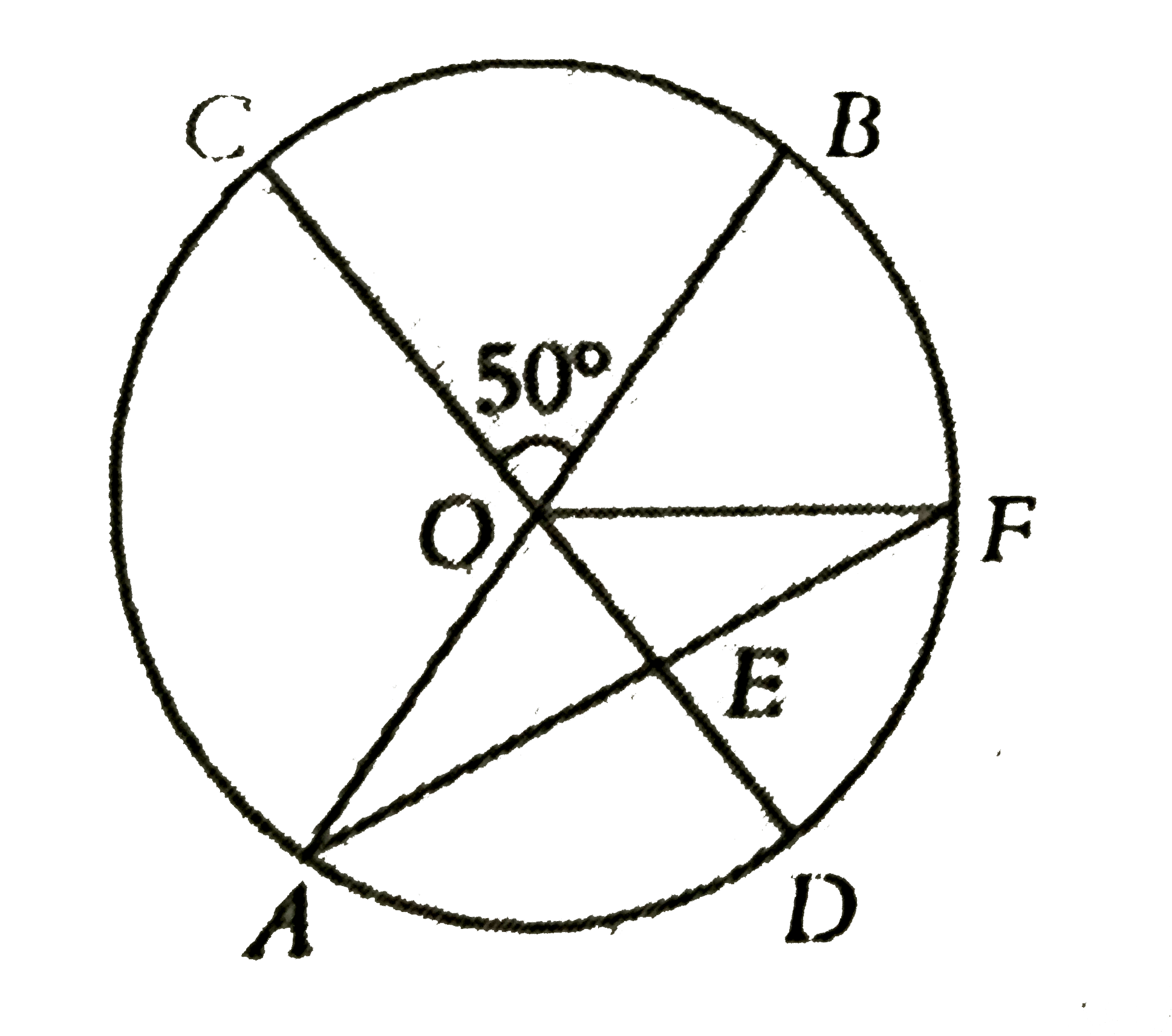
In the above figure , O is the centre of the circle, AB and CD are diameters. `/_ COB =50^(@)=50^(@)` . If E is the midpoint of AF, then find `/_ ADF`
View Solution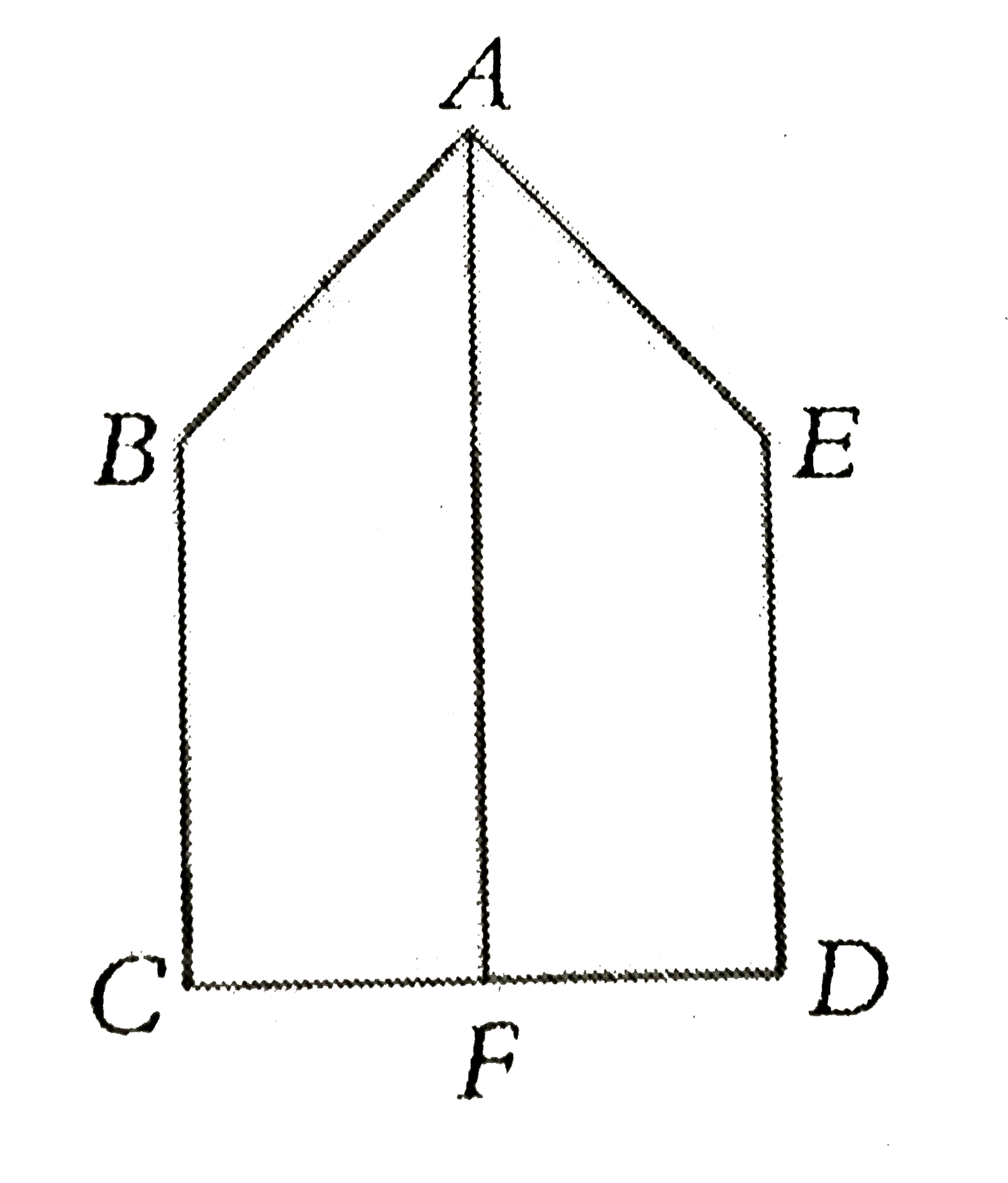
In the figure above (not to scale), ABCDE is symmetrical about AF. If `/_C =90^(@)` and `/_ BAF =45^(@)`, then find the `/_E`.
View Solution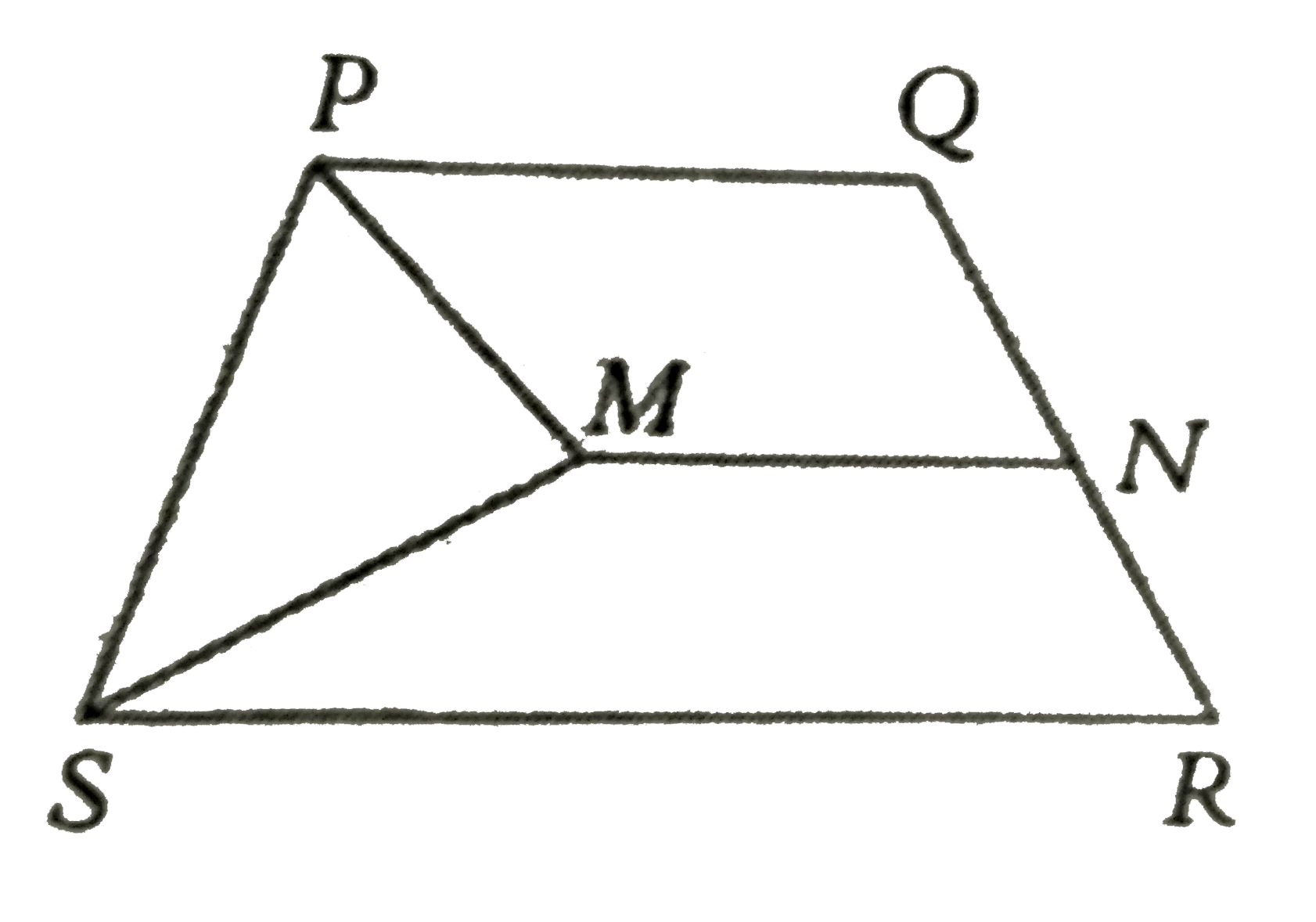
In the given figure, PQRS is an isosceles trapezium and `bar(PQ)||bar(SR)||bar(MN)` If `/_ SPM=70^(@)` and `/_ PQR =110^(@)`, then find `/_ PMN.`
View Solution
CONCEPT APPLICATION (Level 1) questions and complete solutions for chapter GEOMETRY of PEARSON IIT JEE FOUNDATION of Class 8