Complete Solutions to Level 1 of chapter GEOMETRY of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | GEOMETRY |
| PEARSON IIT JEE FOUNDATION | Level 1 |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
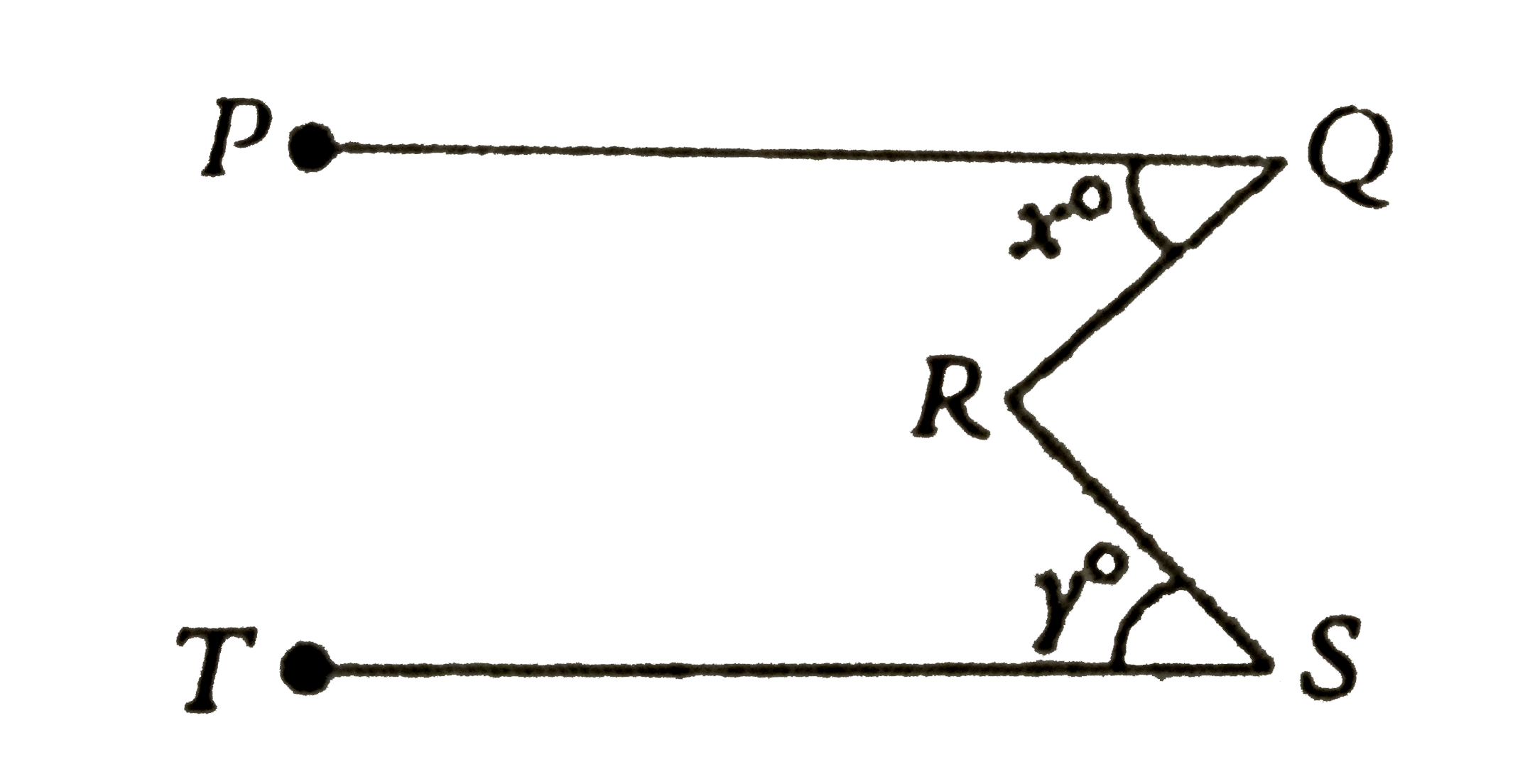
In the figure below (not to scale) , `bar(PQ)||bar(TS)`, reflex `/_ QRS=300^(@)` and `x-y =30^(@)`. The measure of `y` will be
View SolutionIn a triangle ABC, if `/_ A gt /_ B gt /_C` and the measures of `/_A , /_B ` and `/_ C` in degrees are integers, then the least possible value of `/_ A` is
View Solution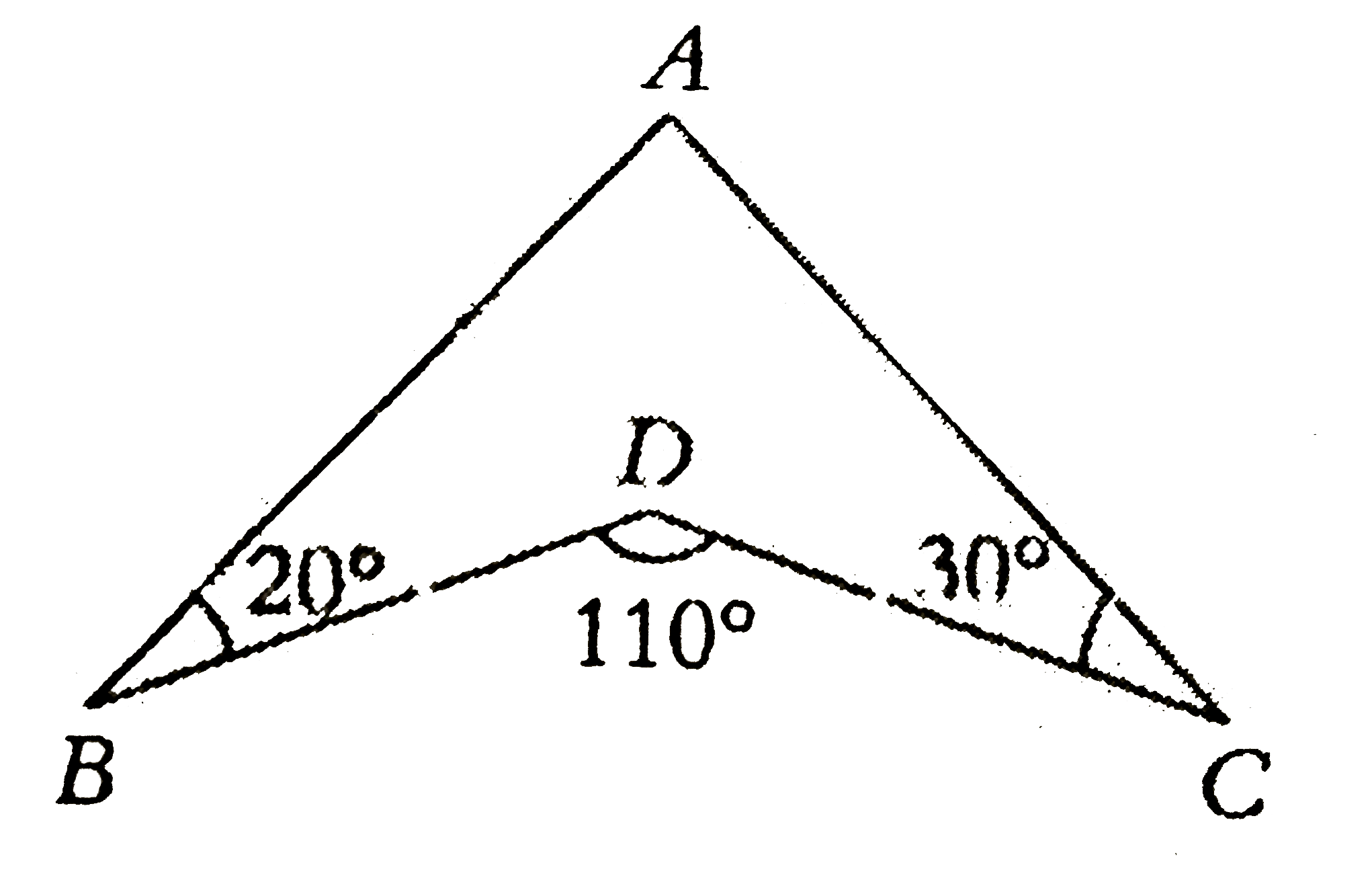
In the above figure, `/_ ABD =20^(@), /_ BDC =110^(@)` and `/_ DCA =30^(@)` . What is the value of `/_ BAC` ?
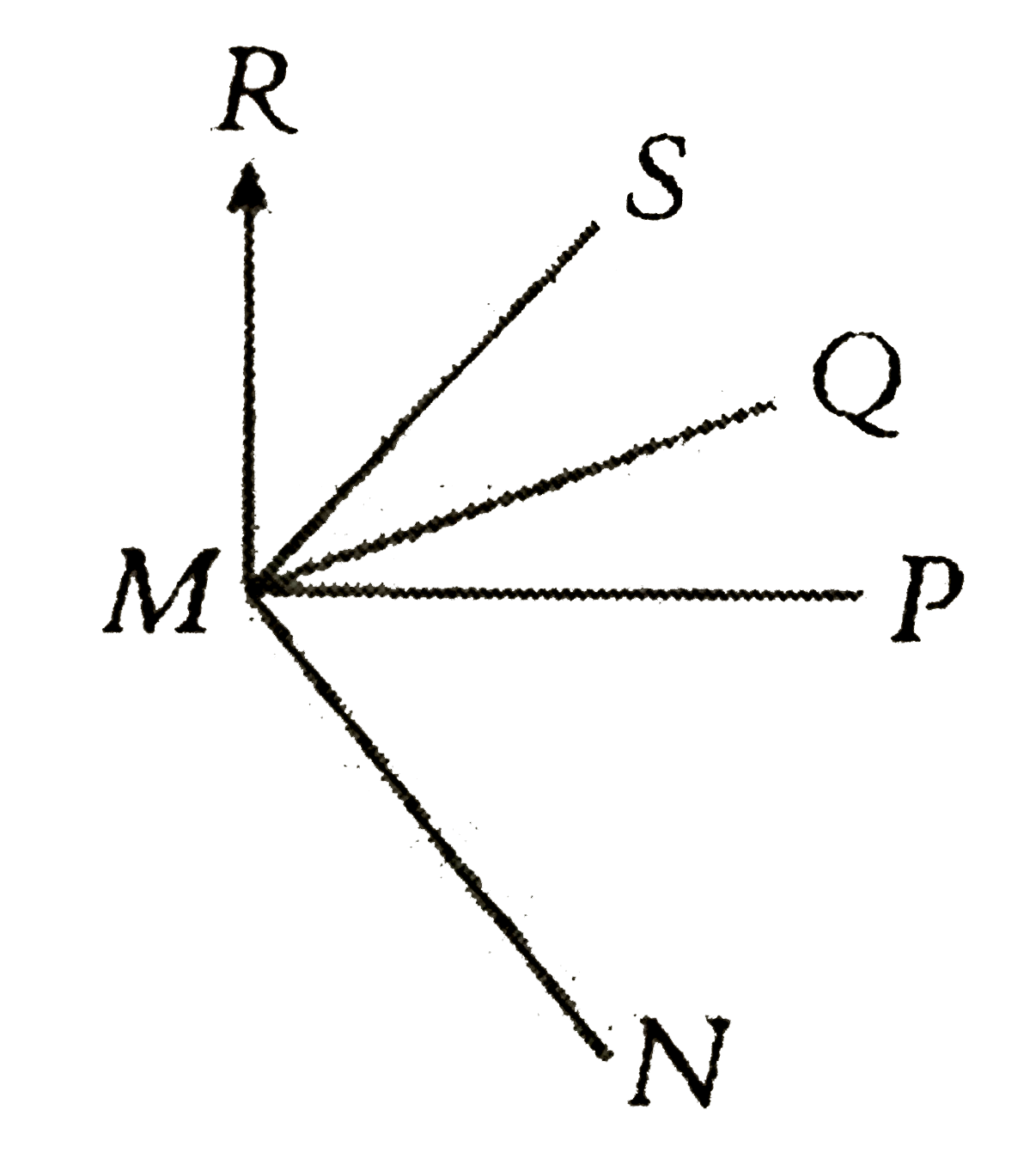
View SolutionIn the figure below (not to scale), `bar(MR )_|_ bar(MP), bar(MQ) _|_ bar(MN)`, and `bar(MS)` is bisector of `/_ RMQ` . If `/_ PMN=50^(@)` , then find the measure of `/_ RMS`.
View Solution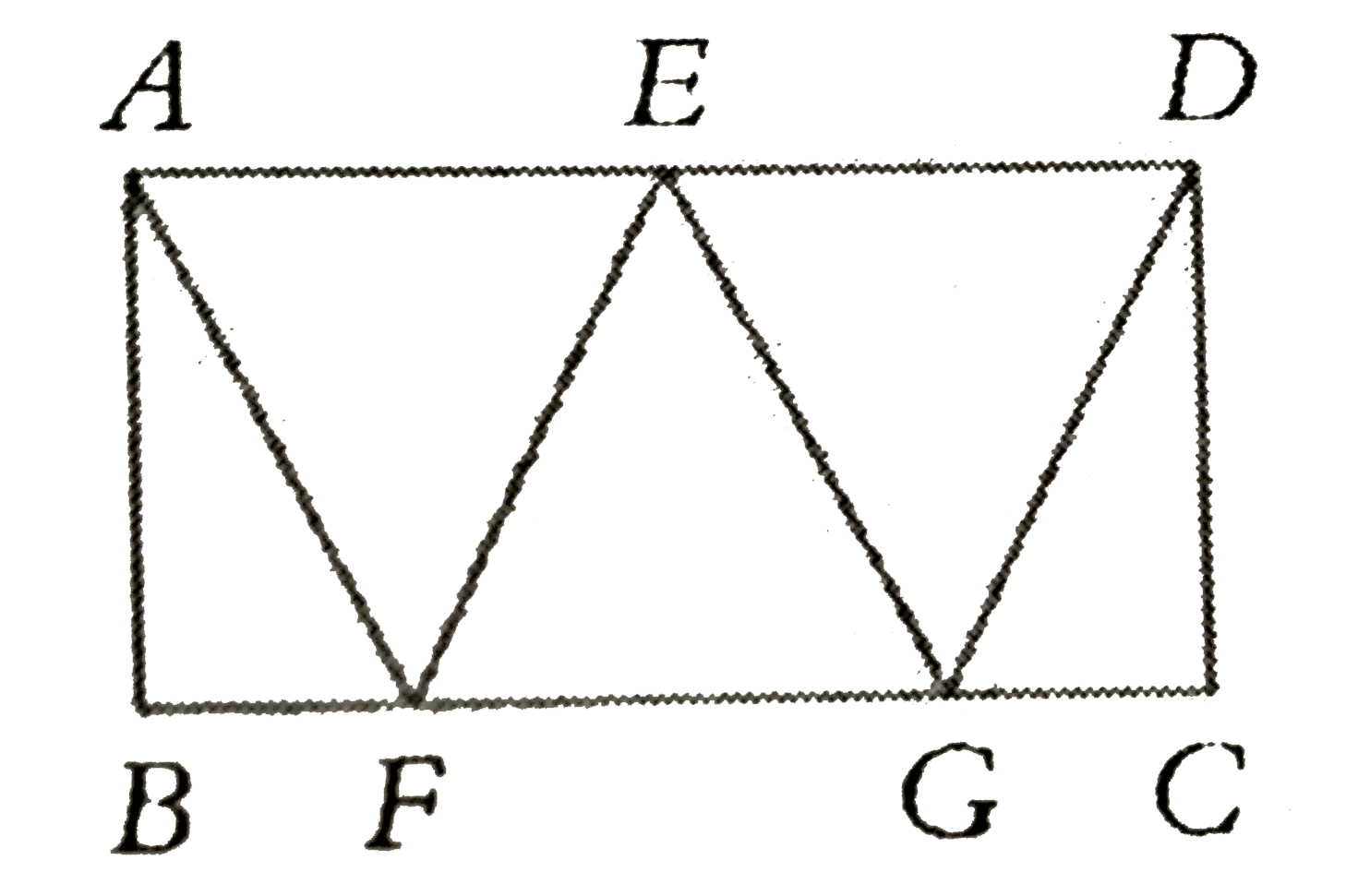 In the figure above (not to scale), `bar(EF)||bar(GD), bar(AF)||bar(EG), bar(AD)||bar(BC)` and `/_ DCG =100^(@)`. If `/_CDG=40^(@)`, then find `/_AEF`.
In the figure above (not to scale), `bar(EF)||bar(GD), bar(AF)||bar(EG), bar(AD)||bar(BC)` and `/_ DCG =100^(@)`. If `/_CDG=40^(@)`, then find `/_AEF`.
View SolutionIn the figure below, `bar(BC)|| bar(EF),BC=EF ` and `DF =AC`. Which of the following congurency axiom(s) is`//` are suitable to prove that `Delta BCA =Delta EFD` ?
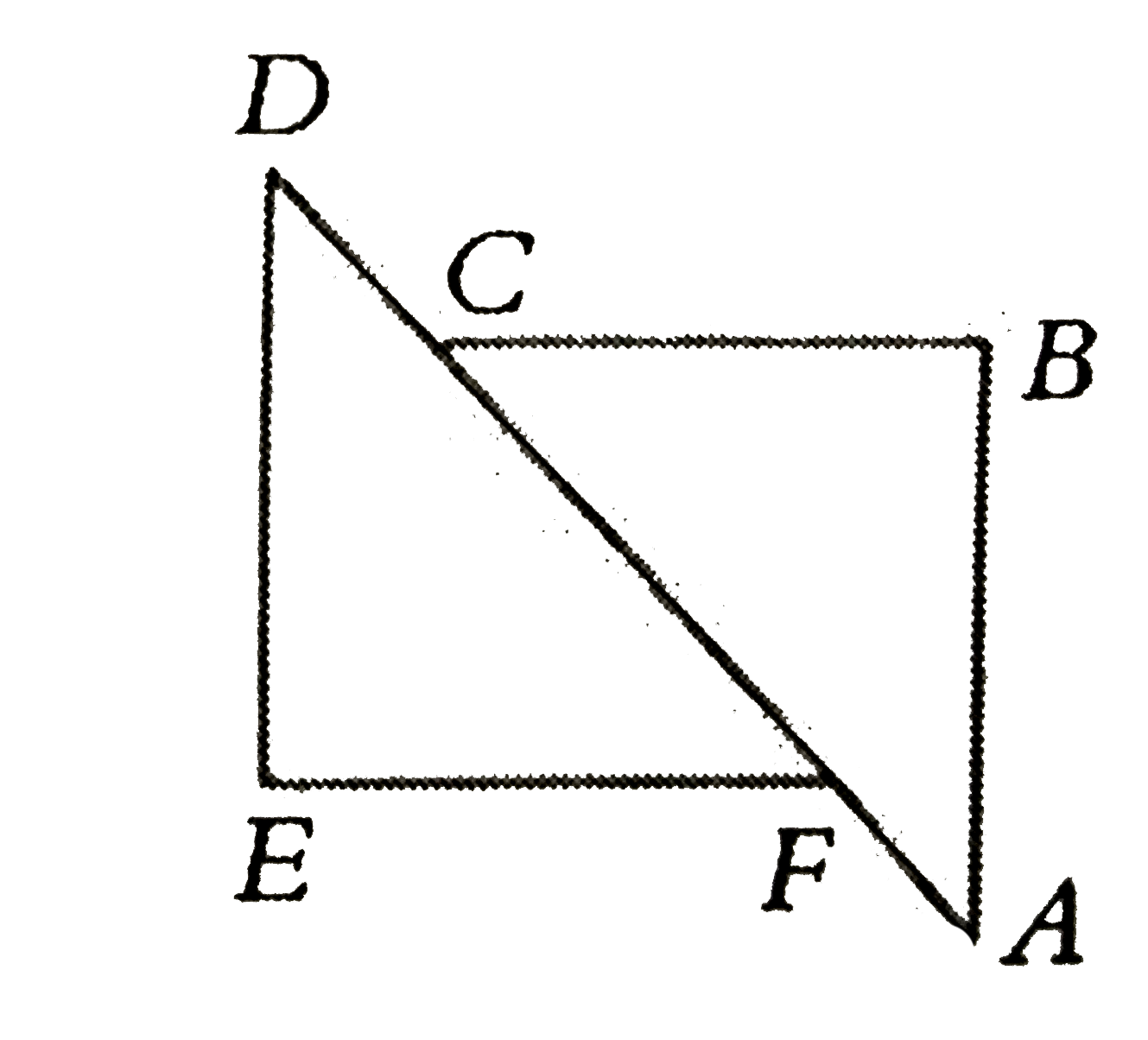
View Solution
In the above figure (not to scale), E and F are the mid points of AB and CD respectively.
`bar(AB) | |bar(CD),bar(BC)||bar(AD),/_ADE =70^(@)`, AND `/_BCE =40^(@), /_DEC` is
View SolutionWhat is the number of lines of symmetry for a parallelogram ?
View SolutionGiven below are some figures. Choose the image of the given figure with respect to the given line from the given choices.

View SolutionIn the given figure , PQ and RS are chords of length 10 cm each intersecting at B . If `anglePBS=90^(@)and` the area of `DeltaPBS` is 32 `cm^(2)` , then the length of BR is ________ .
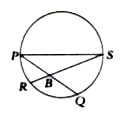
View Solution
In the above figure (not to scale), O is the centre of the circle. `bar(BC)` and `bar(CD)` are equal chords. If `/_ OBC =70^(@)` , then find `/_BAD`.
View Solution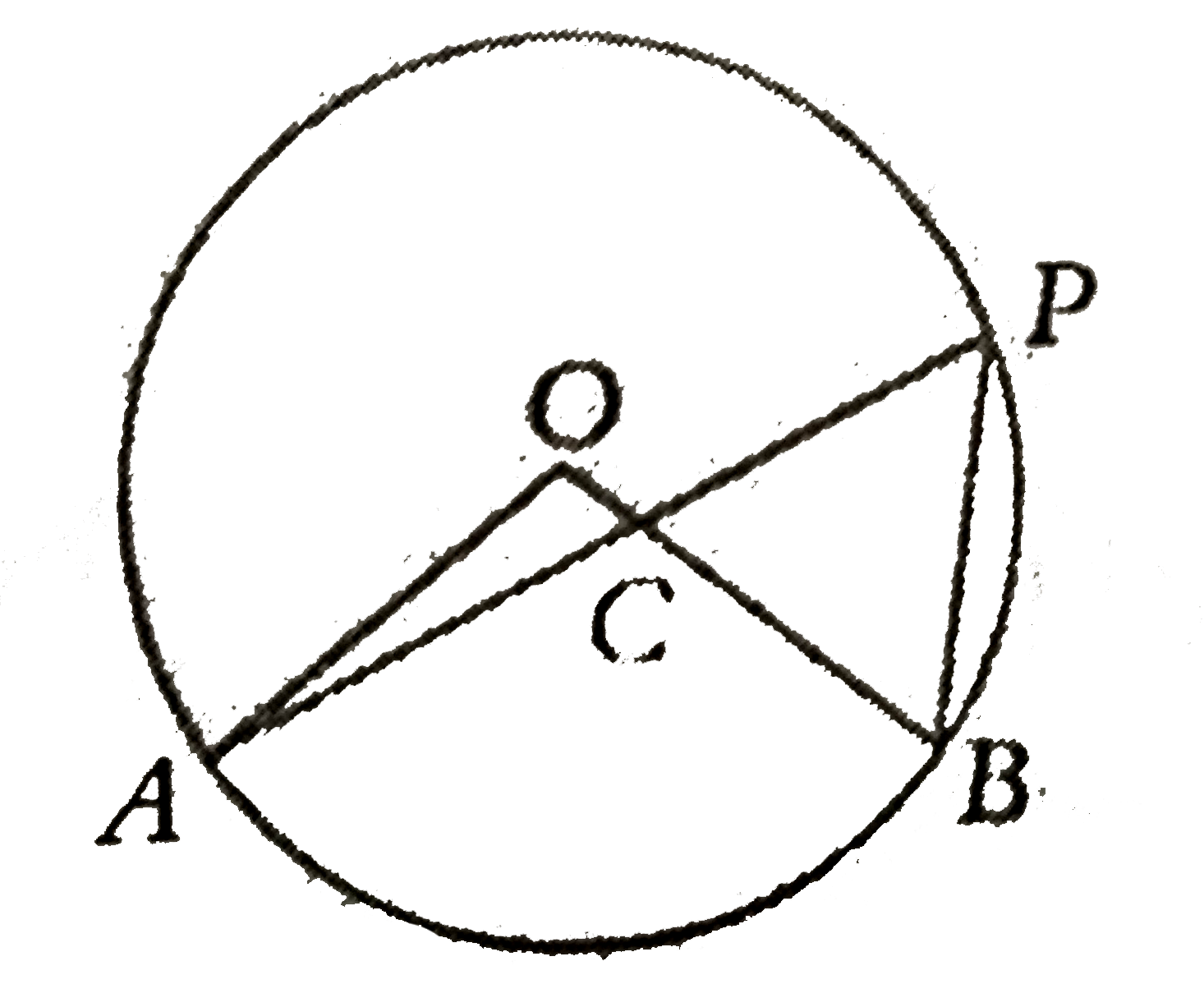
In the above figure (not to scale), O is the centre of the circle. `bar(AP)` and `bar(BP)` are two chords. C is the point of intersection of `bar(AP)` and `bar(OB)`. If `/_ OAC= 30^(@)` and `/_ PBC =80^(@)`, then `/_ AOB=`
View Solution
In the above figure , `overline(AB)andoverline(AC)` are equal chords and `overline(OD)` is perpendicular to `overline(AC)` . If `angleCOD=60^(@)`, then the angle between the chords is ______ .
View Solution
In the above figure, O is the centre of the circle and `AB=CD`. If `/_ APB=110^(@)`, then find the angle made by the chord CD at the centre.
View Solution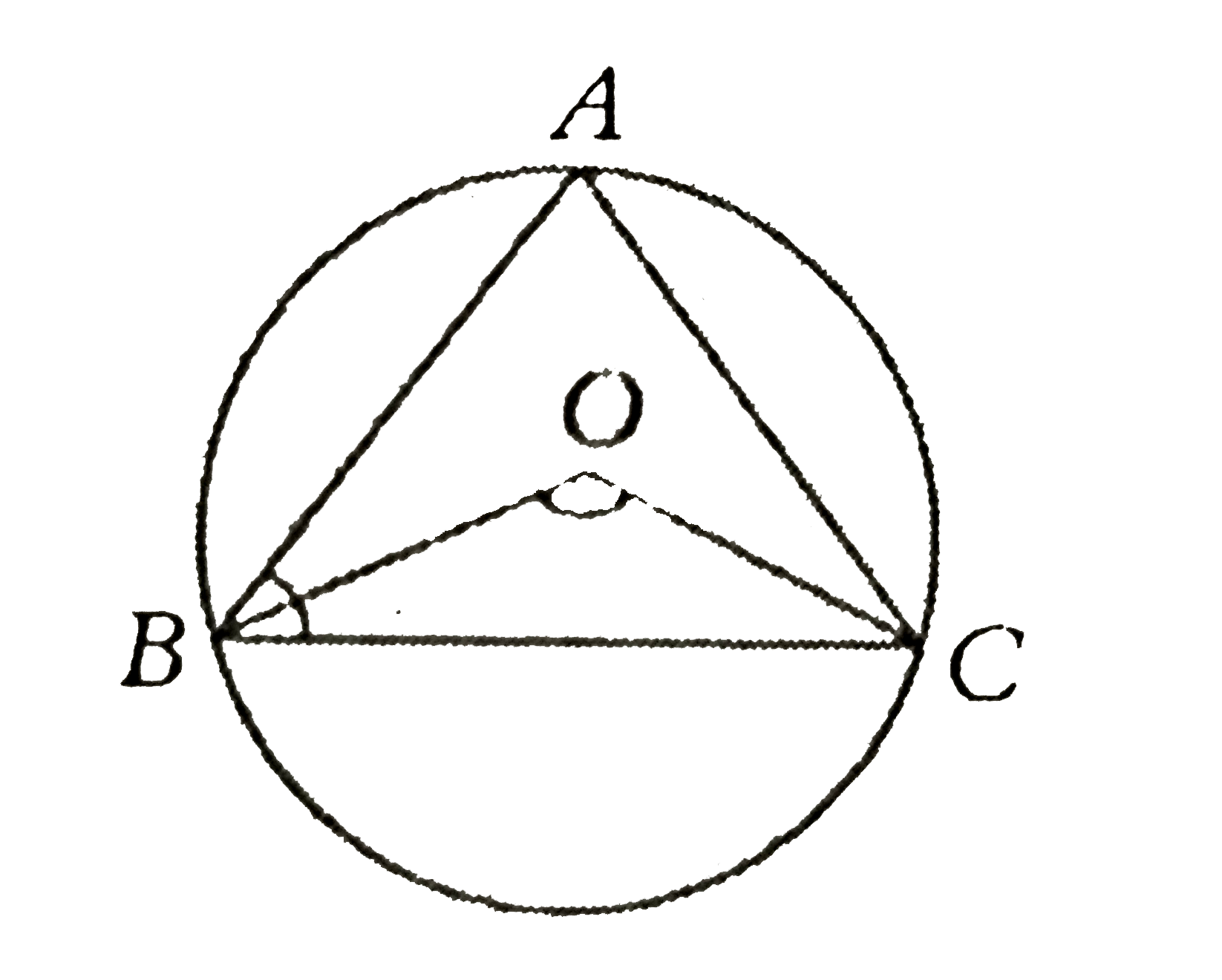
In the above diagram (not to scale), `AB=AC=`. O is the centre of the circle. If `/_ ABC =80^(@)`, then `/_ BOC =`
View Solution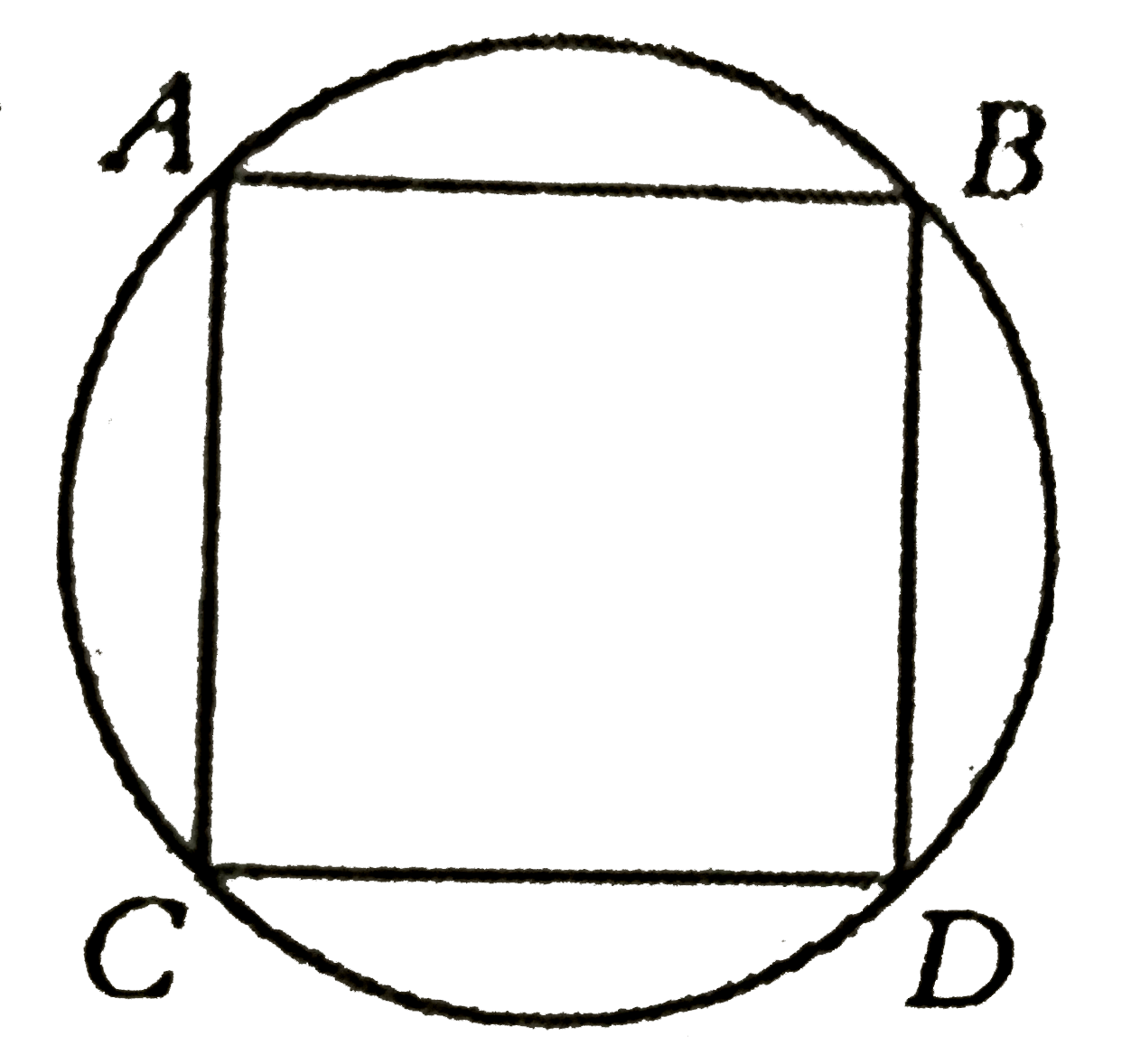
In the figure above (not to scale), `AB=CD` and `/_A =100^(@)`. `/_ C =`
View Solution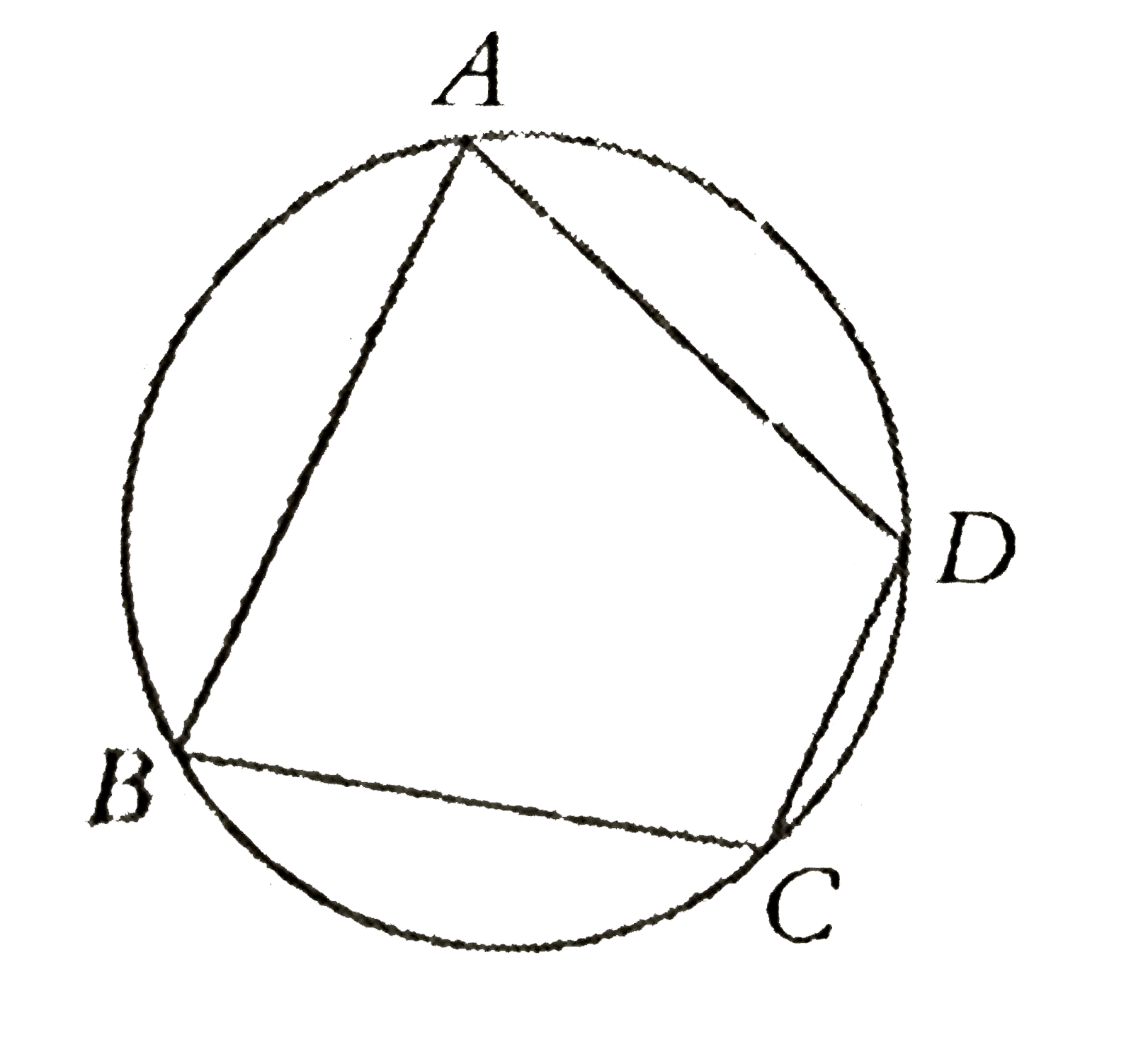
In the above figure, ABCD is a cyclic quadrilateral and `/_BCD =2 /_ BAD`. Find the angle made by the diagonal BD at the centre of the circle.
View SolutionIn the below figure, one part of the line of symmetrcy is given. Recongnise the second part.
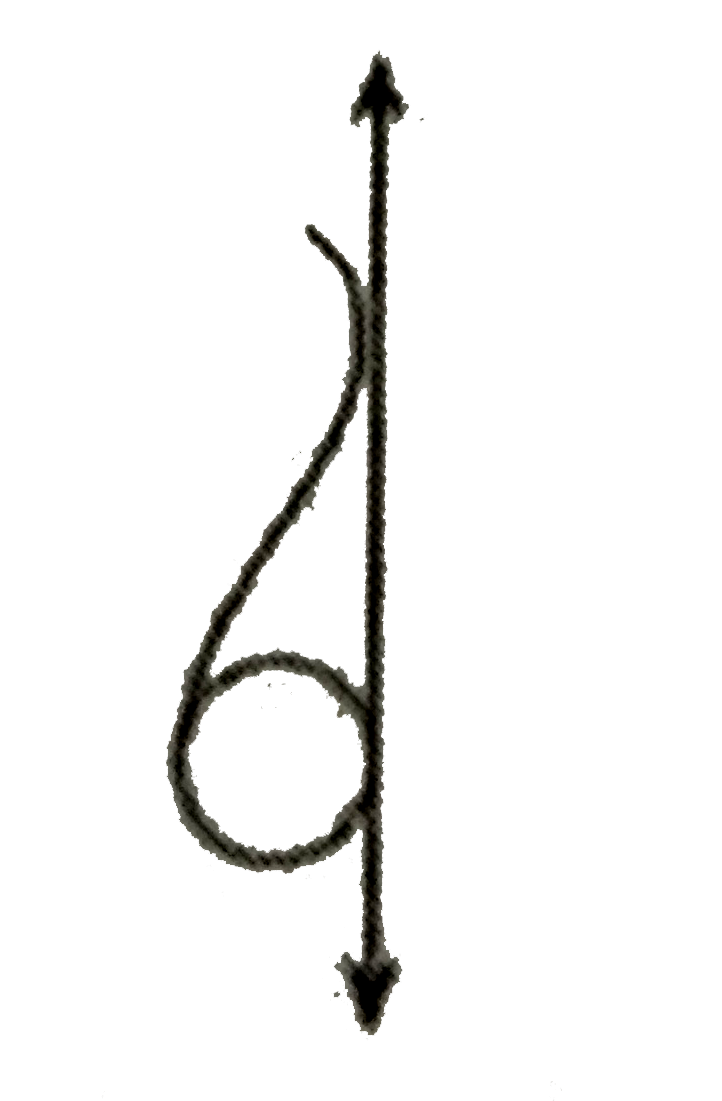
View Solution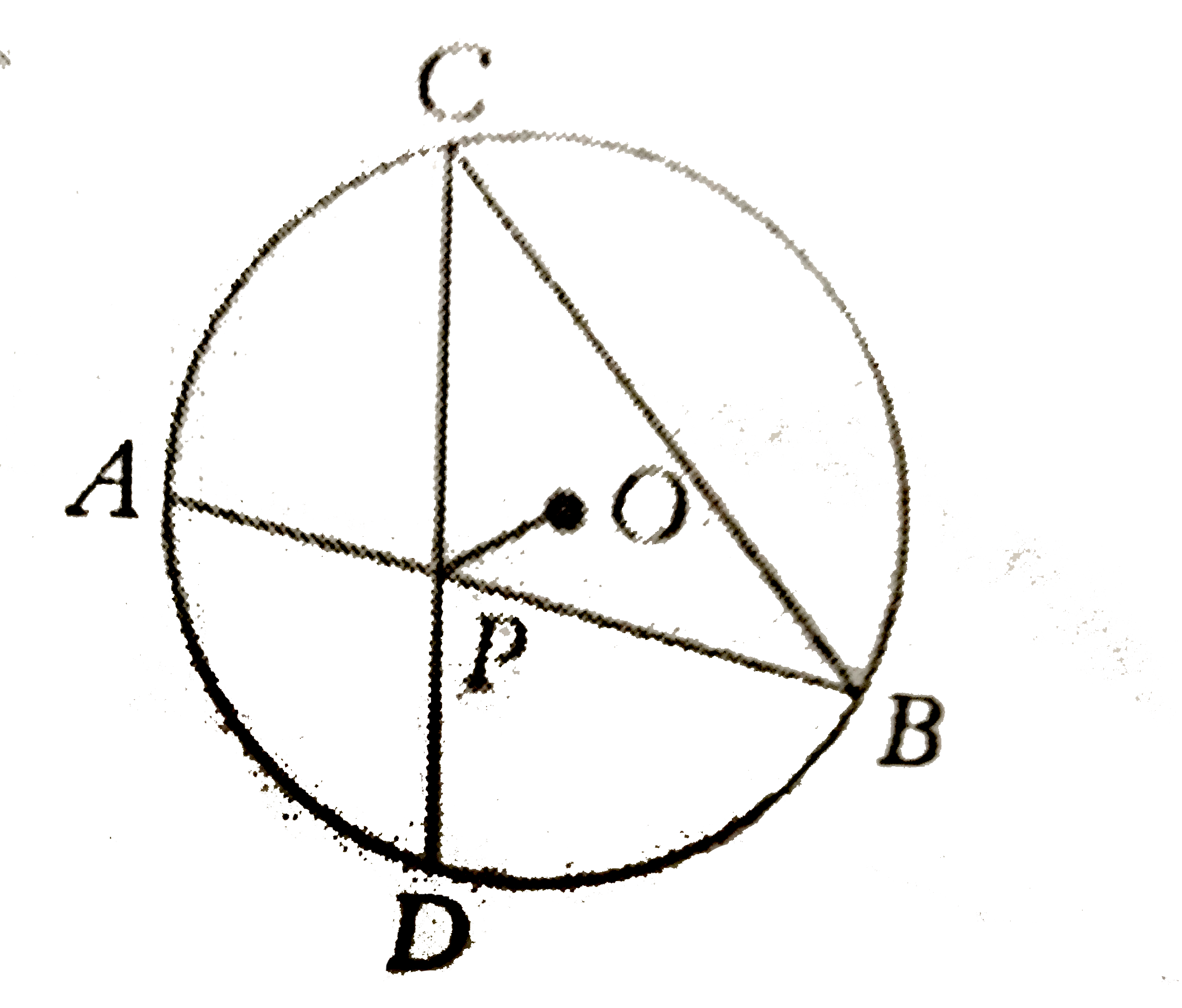 In the above figure , AB and CD are equal chords and O is the centre of the circle. If `/_ OPB =50^(@)`, then `/_ PBD = "____________"`
In the above figure , AB and CD are equal chords and O is the centre of the circle. If `/_ OPB =50^(@)`, then `/_ PBD = "____________"`
View Solution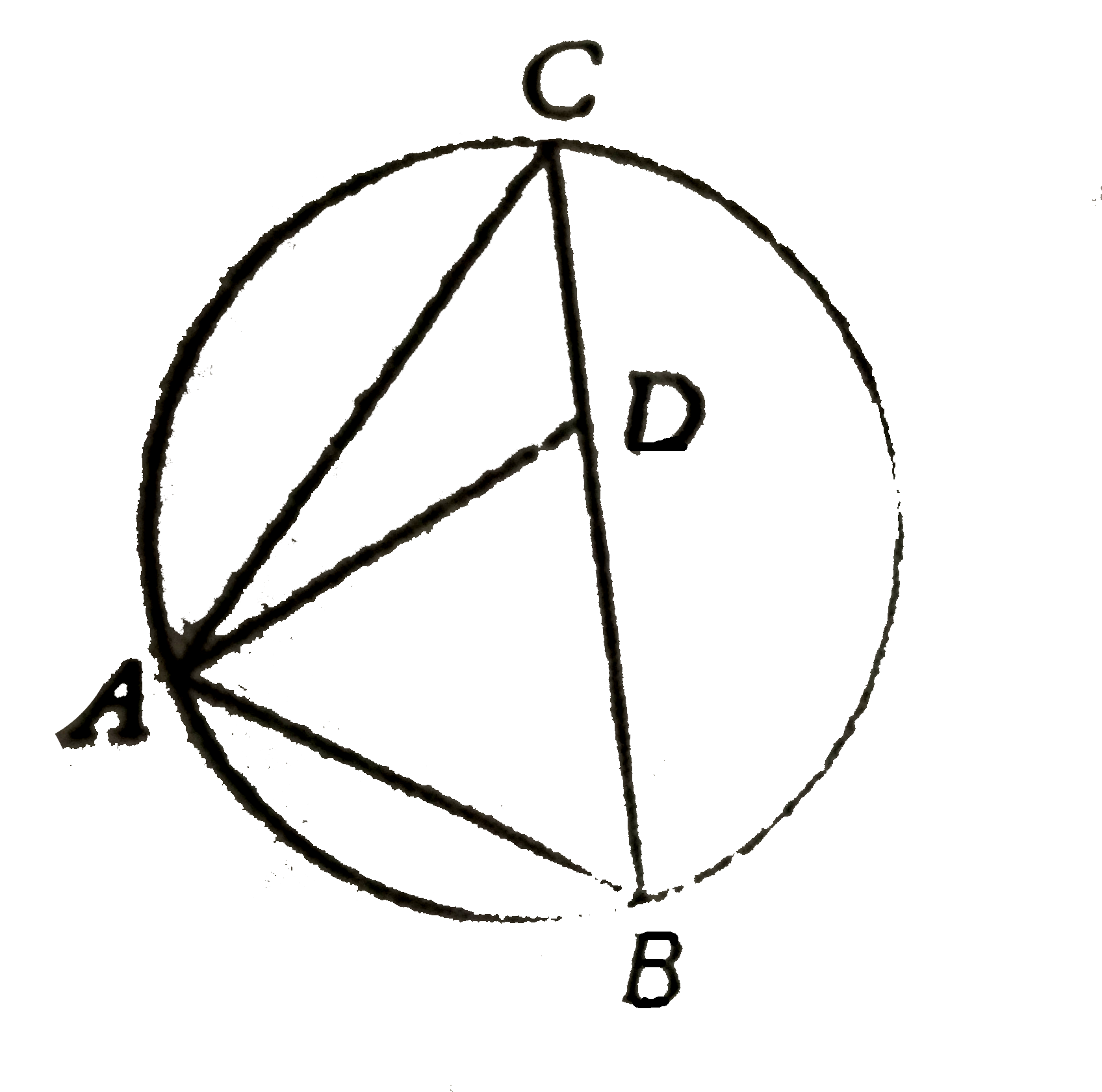 In the given figure, `/_DBA=2 /_DAB = 4/_ CAD`.
In the given figure, `/_DBA=2 /_DAB = 4/_ CAD`.
If `/_ ADC =120^(@)` , then the angle made by AB at the centre of the circle is
View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and `AB=CD`. If `/_MON =120^(@)`, then find `/_ OPN`.
View SolutionIn the following figure ( not to scale), `/_ ADC =60^(@), /_ BAD =80^(@)` and `/_EBC = 2/_PDE`. Find `/_ APE`.
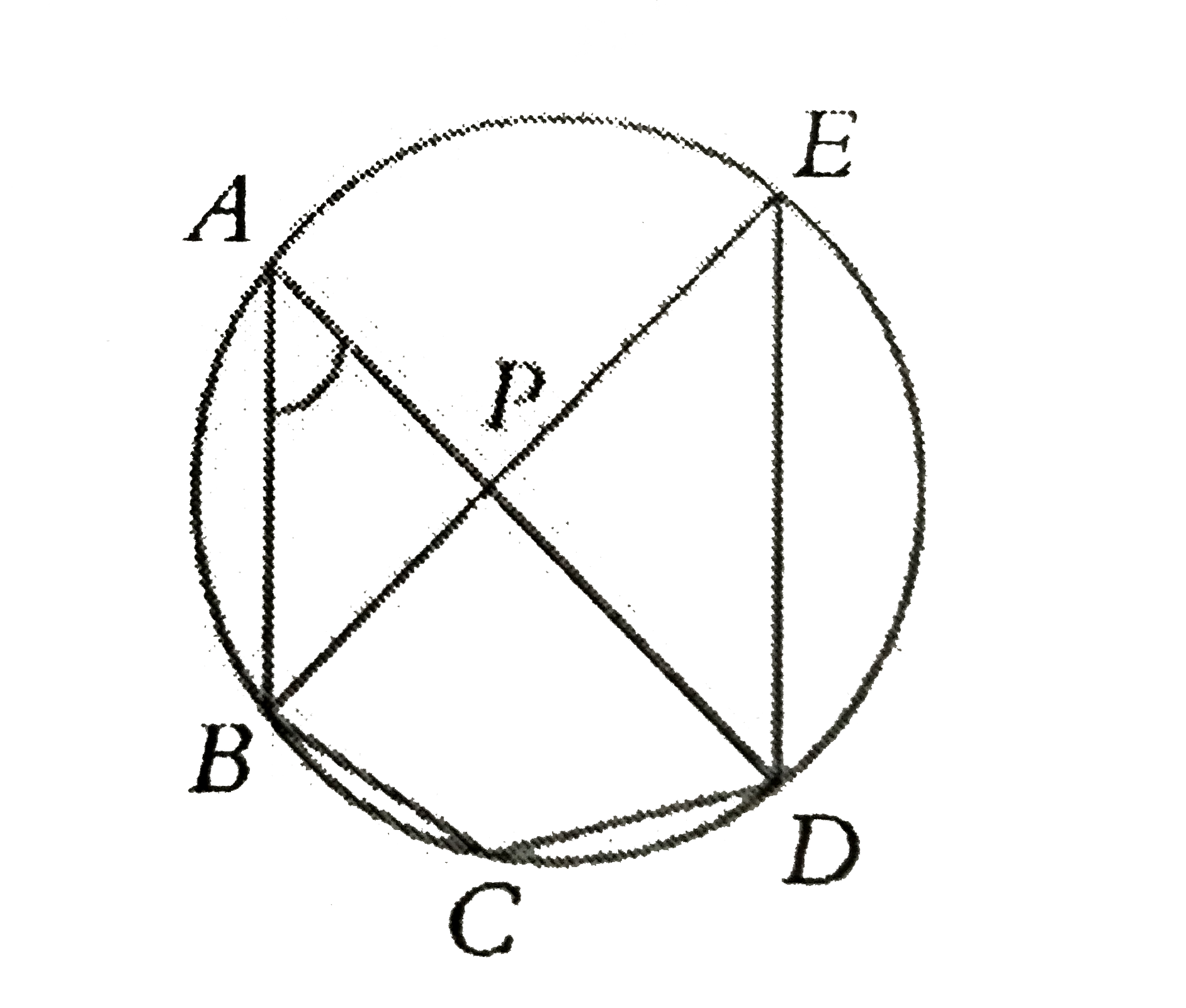
View SolutionHow many lines of symmetry does the above figure have ?
View Solution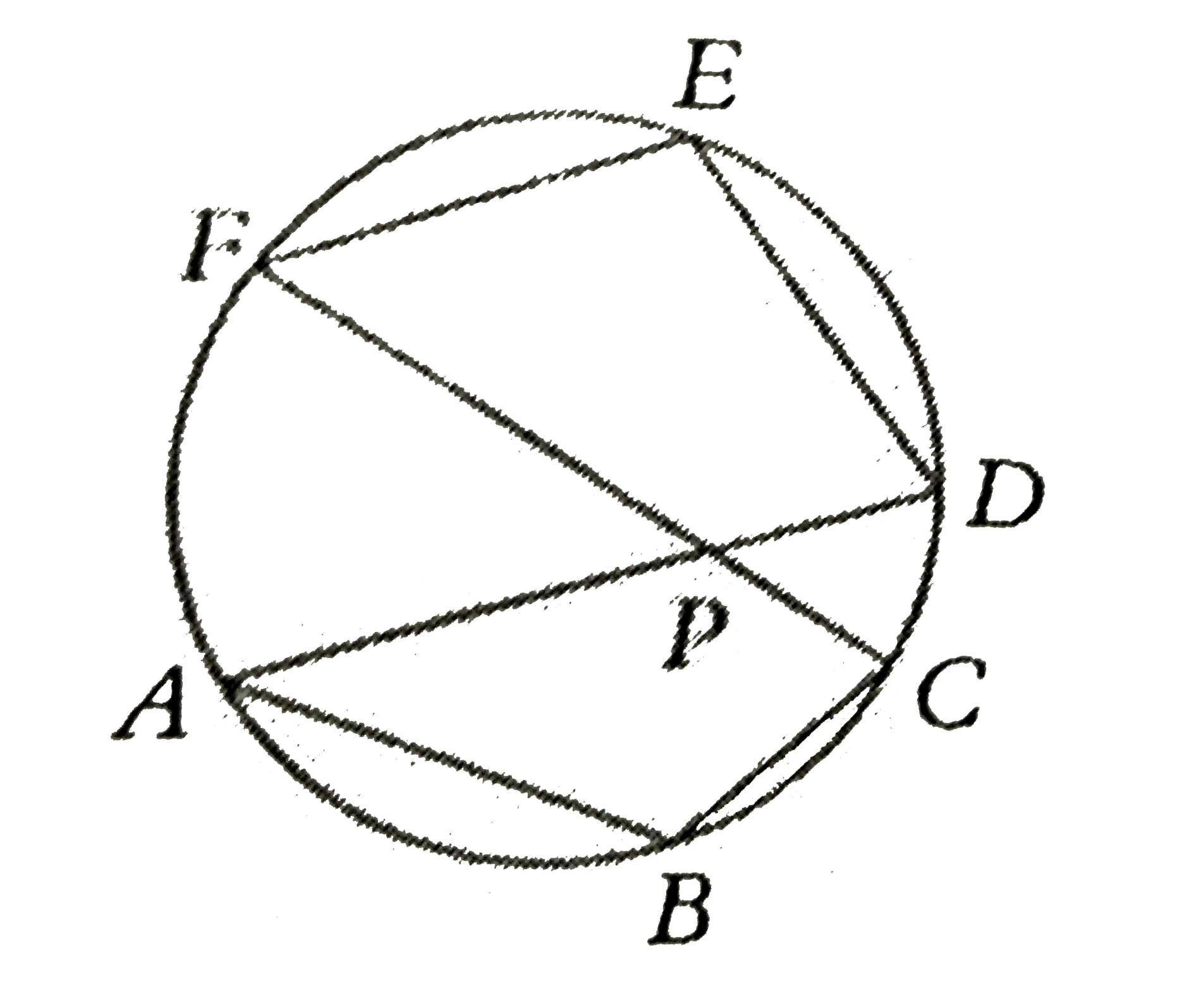 In the above figure (not to scale) `bar(AB),bar(BC),bar(CF),bar(DE)` and `bar(FE)` are chords of the circle. If `/_ ABC =100^(@)` and `/_ FED =110^(@)`, then `/_FPA =`
In the above figure (not to scale) `bar(AB),bar(BC),bar(CF),bar(DE)` and `bar(FE)` are chords of the circle. If `/_ ABC =100^(@)` and `/_ FED =110^(@)`, then `/_FPA =`
View SolutionIn the figure given below, `bar(ED)||bar(AB)` and `bar(EF)||bar(BC)`. If `/_FED =40^(@)` and `/_ DEC =20^(@)`, then the angle made by `bar(BC)` at the centre is
View SolutionThe supplement of an angle and the complement of another have a sum equal to half of a complete angle. If the greater angle is `10^(@)` more than the smaller , find the smaller angle.
View SolutionABCD is a trapezium in which `AB ||CD, AB =20cm, BC =10` cm, `CD =10` cm and `AD =10` cm . Find `/_ADC`
View SolutionP is an interior point of quadrilateral ABCD and `AB =3.5`cm, `BC =4 cm, CD=4.8 cm ` and `AD =3.7 ` cm . Then which of the following can be the possible value of `(AP+BP+CP+DP)` ?
View SolutionThe angles of a triangle are in the ratio `2:3:4` . Find them
The following are the steps involved in solving the above problem.
Arrange them in sequential order from the first to the last.
(A) `2x+3x+4x=180^(@)`
`implies 9x= 180^(@)implies x=20^(@)`
(B) Let the angles be A,B and C. Given `A:B:C=2:3:4`
`implies A=2x,B=3x=C=4x`
(C ) We know that the sumf of the angles of a triangle is `180^(@), ie., A+B+C=180^(@)`
(D) The angles are `:A=2(20^(@))=40^(@),B=3(20^(@))= 60^(@)` and `C=4(20^(@))=80^(@)`.
View SolutionProve that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
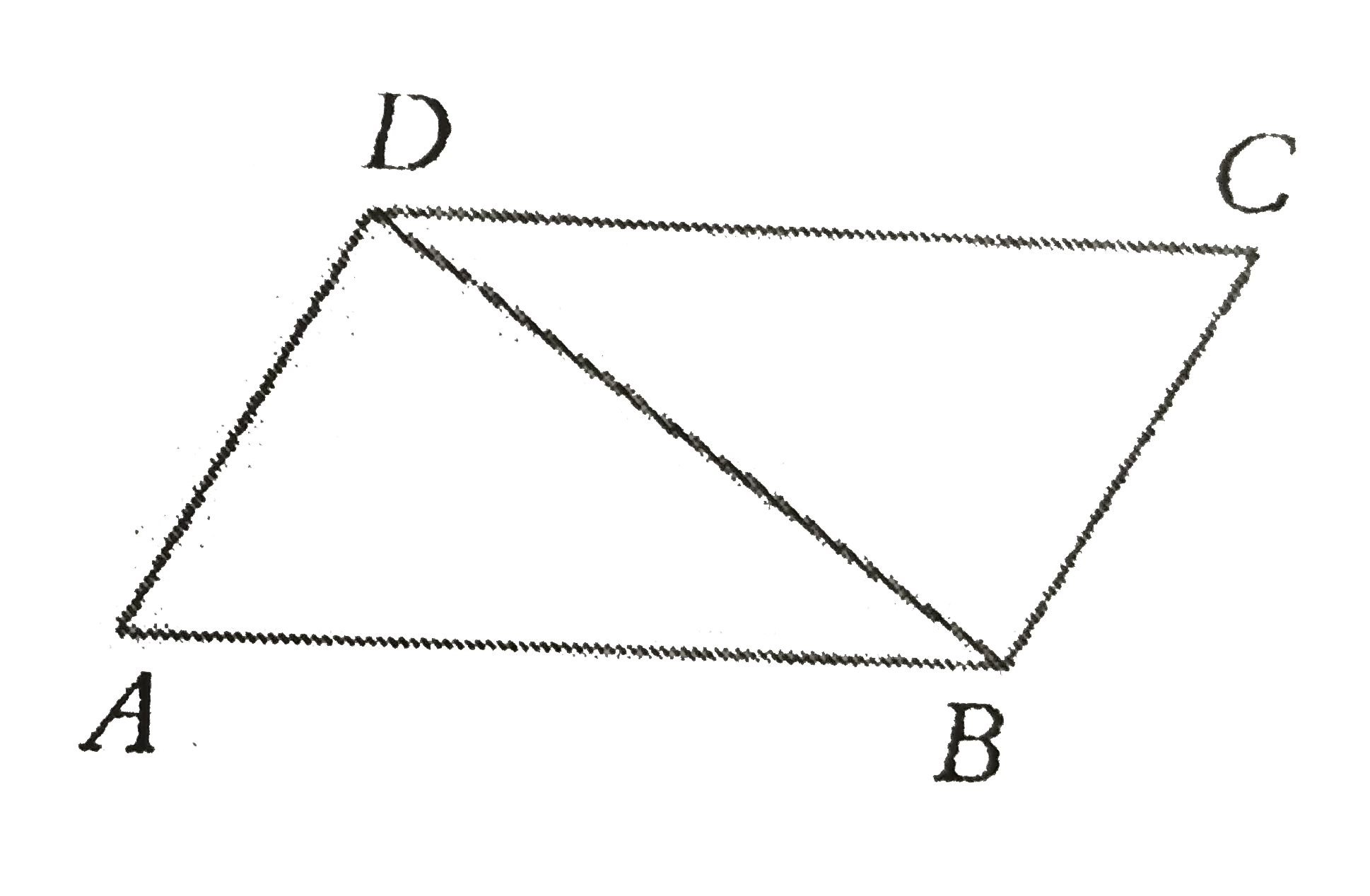
(A) By SSS conguruence property , `Delta DAB ~= Delta BCD`.
(B) Let ABCD be a parallelogram and join BD.
(C ) `AB=CD,AD=BC`(opposite sides of parallelogram) and `BD =BD` (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
View Solution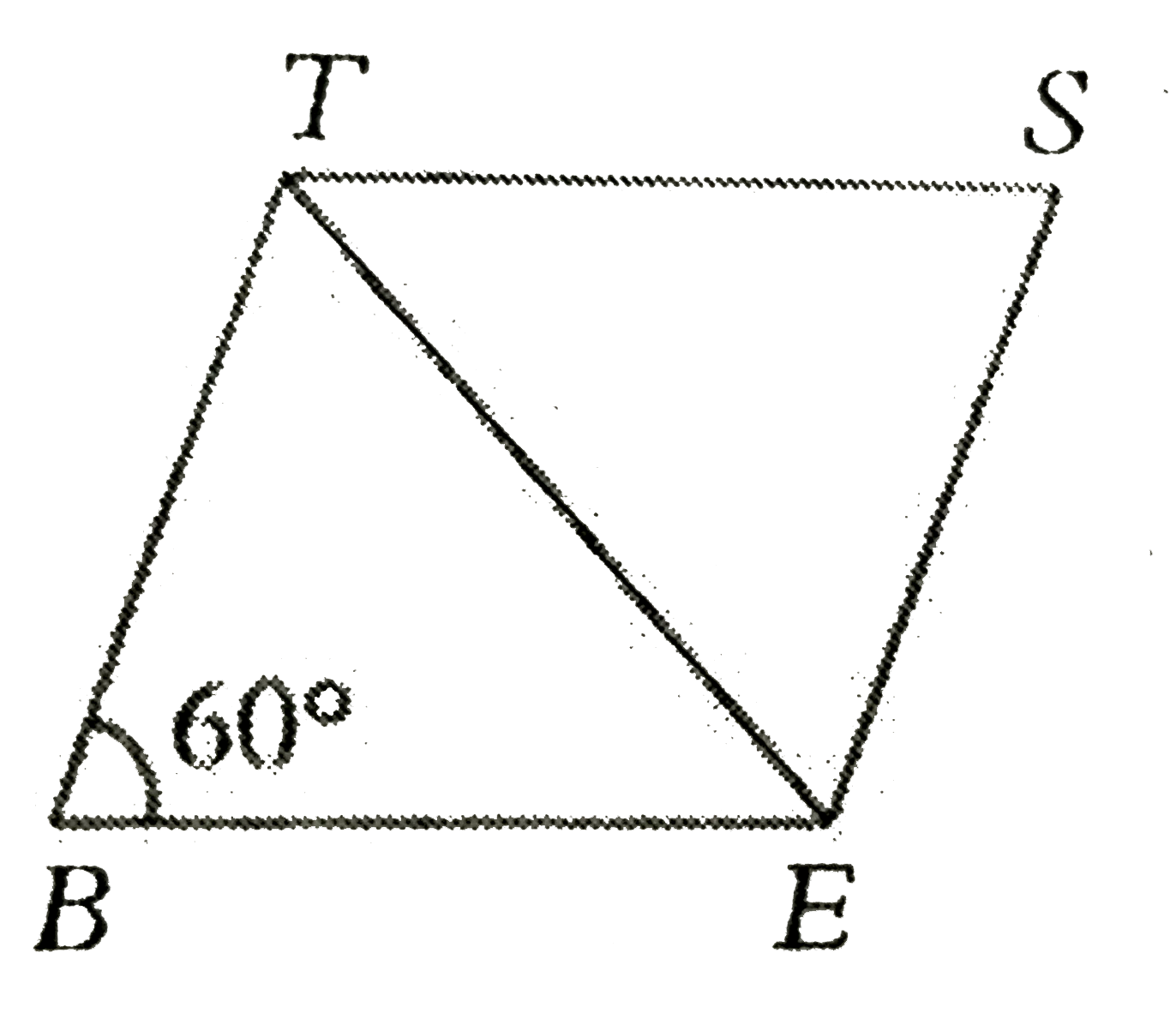
In a rhombus BEST,if `/_ B=60^(@)` and `BT =6cm`, then find the length of the diagonal TE.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) `implies Delta` BTE is an equilateral triangle.
(B) Join T and E
(C ) In `Delta BET, BT=BE implies /_ BTE =/_ BET =(180^(@)-60^(@))/(2)=60^(@) ( :' /_ B=60^(@))` .
(D) `TE=6 `cm
View SolutionThe following sentences are the steps involved in construction of the incircle for the triangle XYZ in which `/_Y =90^(@), XZ=6` cm and `YZ =4` cm.
Arrange them in sequential order from the first to the last.
(A) Mark the foot of the perpendicular from I onto YZ as D.
(B) Construct the triangle XYZ with `/_ Y =90^(@),XZ=6` cm and `YZ =4 cm`.
(C ) Draw a circle with I as the centre and ID as radius. This is the required incircle.
(D) Draw the bisectors of `/_ X, /_ Y` and `/_Z` and mark their point of concurrence as I.
View Solution
Level 1 questions and complete solutions for chapter GEOMETRY of PEARSON IIT JEE FOUNDATION of Class 8