Complete Solutions to TEST YOUR CONCEPTS ( SHORT ANSWER TYPE QUESTIONS) of chapter GEOMETRY of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | GEOMETRY |
| PEARSON IIT JEE FOUNDATION | TEST YOUR CONCEPTS ( SHORT ANSWER TYPE QUESTIONS) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |

In the above figure, AB is parallel to CD. P and R are the points on AB and CD respectively. Q is in between AB and CD. Find the value of x in degrees
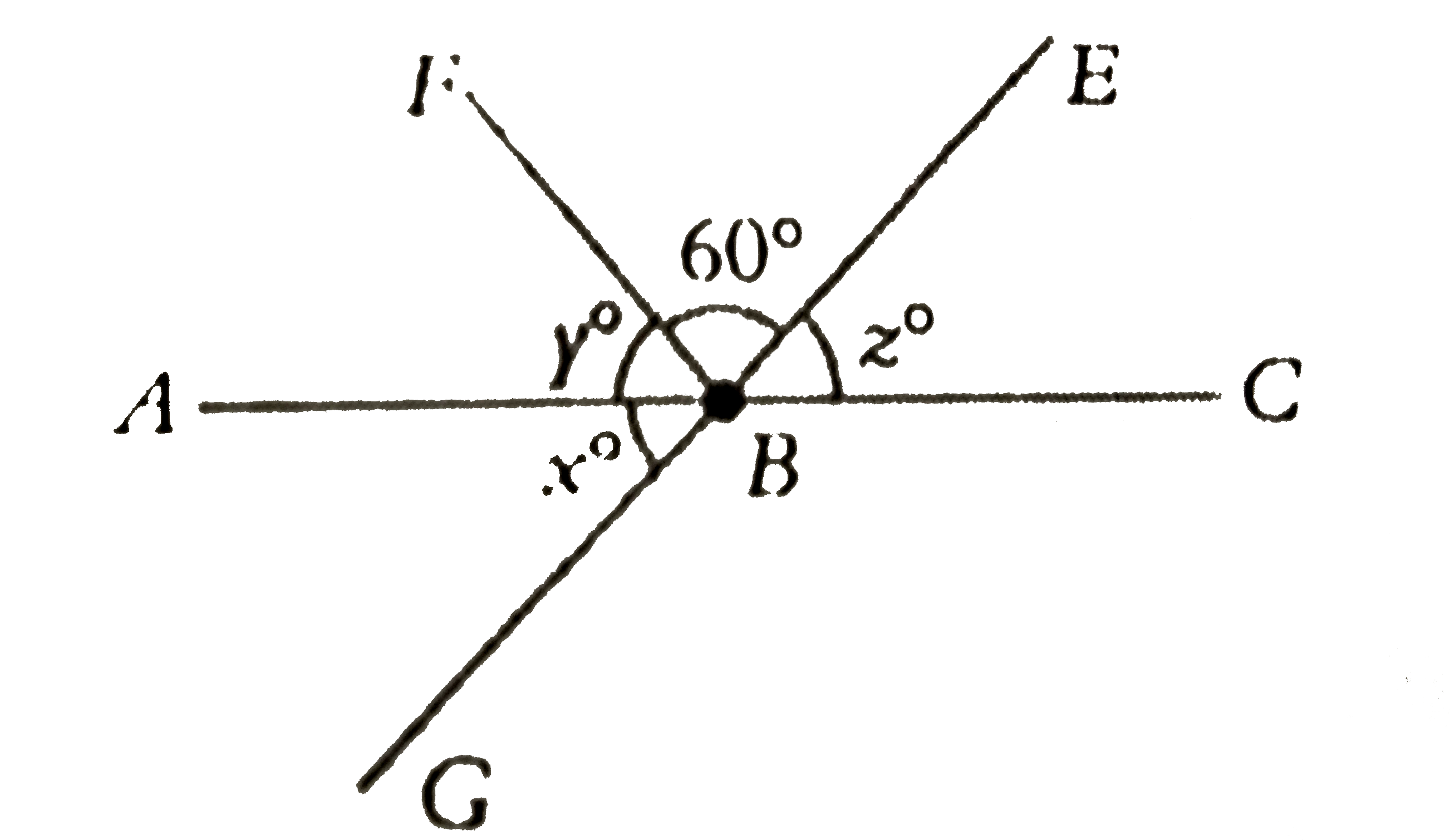
View SolutionIn the figure below ( not to scale), ABC is a straight line. If `/_ FBE =60^(@), /_ CBG =120^(@), /_ ABG = x^(@), /_ ABF= gamm^(@)` and `/_ CBE = z^(@) = 2 gamma^(@)`, then `( x^(@)+z^(@)) : gamma^(@)` is
View SolutionIn the figure below , `overline(EF)||overline(GH)`. If `overline(GI)` is the transversal , `angleIGH=y^(@),andangleFIG=3y^(@)` , then the ratio of the supplement of y to its complement is _______.

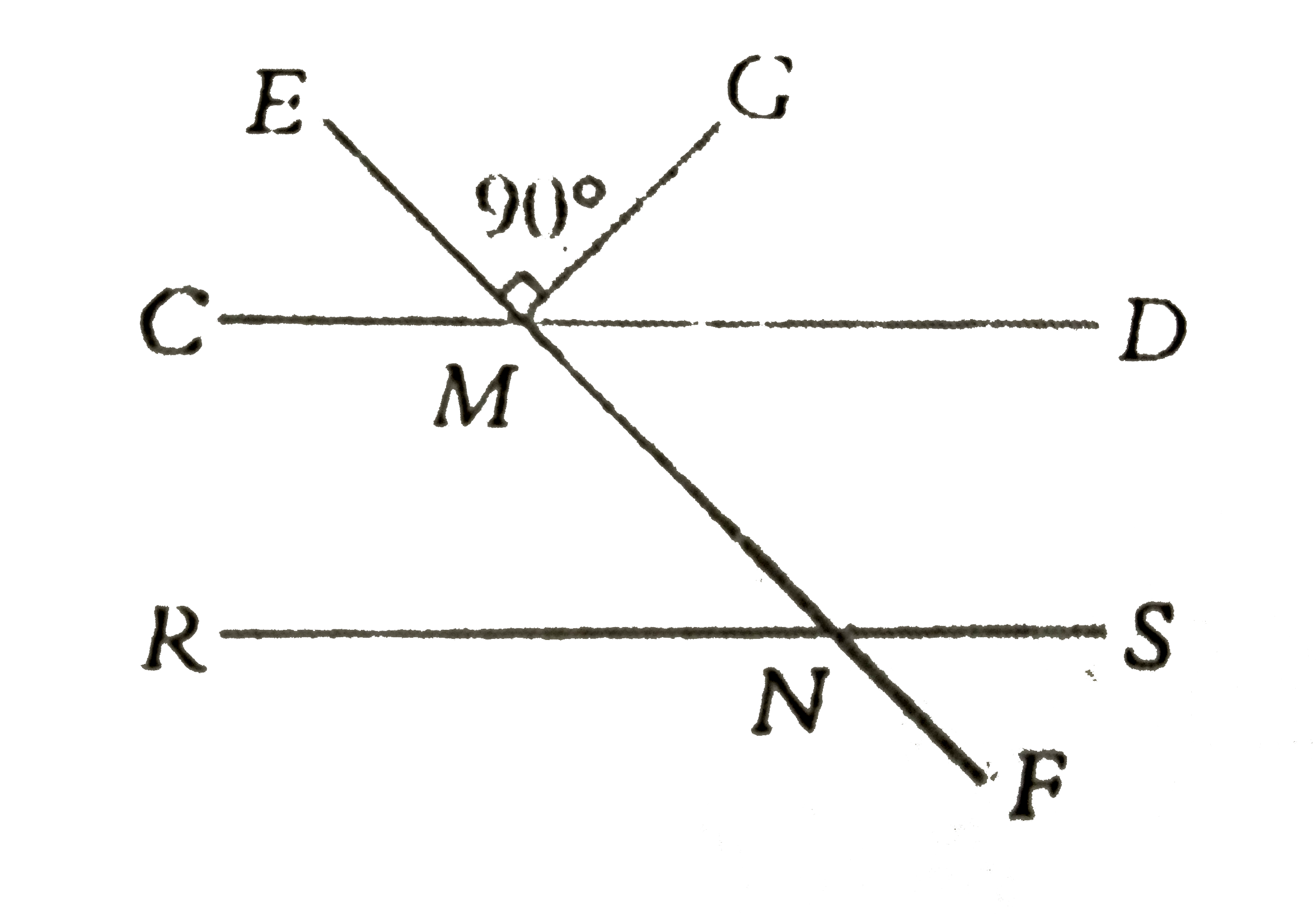
View SolutionIn the figure below ( not to scale) `bar(CD)||bar(RS) /_EMG=90^(@),/_GMD= gamma^(@),/_CME= x^(@) ` and `gamma^(@)=(x^(@))/(2)`. `/_ FNS : /_FNR `is
View Solution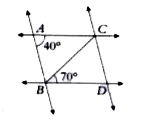
In the above figure (not to scale) , `overline(AB)||overline(CD)andoverline(AC)||overline(BD)`. If `angleBAC=40^(@)andangleCBD=70^(@)`, then `angleBCD=`_______.
View Solution
In the above figure , DF is parallel to MN . EGH is an isosceles triangle , where `EG=EHandangleGEH=50^(@)`. If EM and EN are the bisectors of the `angleDEGandangleFEH` , then
(i) Show that `angleDEM=angleFEN`.
(ii) Show that `angleGEM=angleHEN`.
View Solution
In the above `Delta ABC` ( not to scale ), OA is the angle bisector of `/_ BAC` . If `OB=OC,/_OAC=40^(@)` and `/_ ABO=20^(@)`. If `/_ OCB=(1)/(2) /_ ACO,` then find `/_ BOC.`
View Solution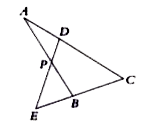
In the given figure , AB and DE are straight lines . `angleBAC=40^(@),angleBPD=110^(@),andangleDEC=40^(@)`. Find `angleACE`.
View SolutionIn the following figure ,ABCD is a parallelogram . Find the value of r .
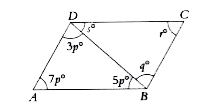
View SolutionThe angles of a quadrilateral ABCD are `x^(@),(x+1)^(@),(x+2)^(@)` and `(x+3)^(@)`, taken in the same order. Then the quadrilateral ABCD is necessarily a
View SolutionMN and PS are two euqal chords of a circle drawn on either side of centre O of the circle .Both the chords are produced to meet at point A . If the radius of the circle is 10 cm , MN =12 cm , and OA =17 cm , then find NA.
View Solution
In the figure above (not to scale), AB is the diameter of the circle with centre O. If `/_ ACO=30^(@),` then find `/_ BOC`.
View Solution
In the figure (not to scale ), O is the centre of the circle and `/_OBA=30^(@)`. Find `/_ ACB`
View Solution
In the figure above (not to scale ), AB= AC and `angleBAO=25^(@)`. Find `angleBOC`, if O is the centre of the circle .
View Solution
In the above figure (not to scale), O is the centre of the circle AC and OB are parallel lines .If `angleACO=80^(@)` , then find `angleADO` .
View Solution
TEST YOUR CONCEPTS ( SHORT ANSWER TYPE QUESTIONS) questions and complete solutions for chapter GEOMETRY of PEARSON IIT JEE FOUNDATION of Class 8