Complete Solutions to All Questions of chapter UNDERSTANDING PHASE-III (SPECIAL TYPES OF QUADRILATERALS) of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | UNDERSTANDING PHASE-III (SPECIAL TYPES OF QUADRILATERALS) |
| Mathematics | All Questions |
| Number Of Questions | 87 |
| Academic Year | 2023-24 |
In a parallelogram the sum of any two adjacent angles is `180^0dot`
View SolutionIn a parallelogram, two adjacent angles are supplementary.
View SolutionTwo adjacent angles of a parallelogram are equal. What is the measure of each?
View SolutionIn a parallelogram `A B C D ,\ /_D=115^0,` determine the measure of `/_A\ a n d\ /_Bdot`
View SolutionTwo adjacent angles of a parallelogram are as `2: 3.` Find the measures of all the angles.
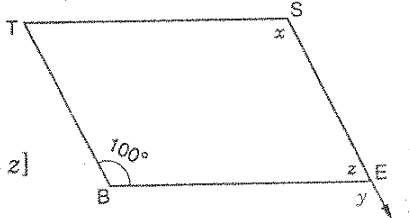
View SolutionIn Figure, `B E S T` is a parallelogram. Find the values of `x ,\ y\ a n d\ zdot`
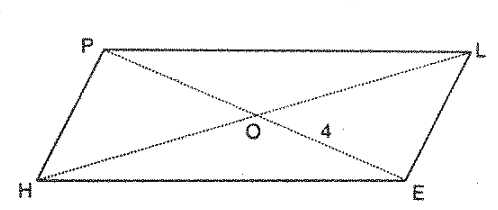
View SolutionIn Figure, `H E L P` is a parallelogram. If `O E=4c m\ a n d\ H L` is 5cm more then `P Edot` Find `O Hdot`
View SolutionIn Figure, `R I N G` is a parallelogram, if `/_R=70^0,` find all other angles.

View SolutionIn Figure, `A B C D` is a parallelogram in which `/_D A O=40^0,\ /_B A O=35^0\ a n d\ /_C O D=65^0dot` Find: `/_A B O\ ` (ii) `/_O D C` (iii) `/_A C B` (iv) `/_C B D`

View SolutionIn Figure, `A B C D` is a parallelogram in which `/_D A B=75^0,\ /_D B C=60^0dot` Calculate `/_C D B\ a n d\ /_A D Bdot`
View SolutionIn a parallelogram `A B C D ,` the bisectors of `/_A\ a n d\ /_B` meet at `Odot` Find `/_A O Bdot`
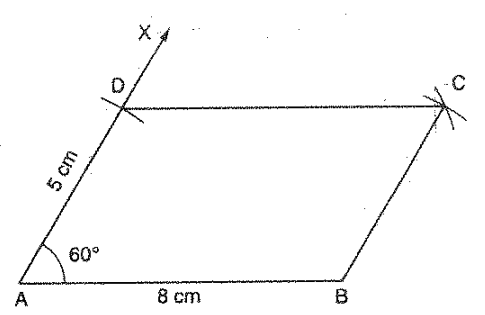
View SolutionDraw a parallelogram `A B C D` in which `A B=8c m ,\ A D=5c m\ a n d\ /_A=60^0dot`
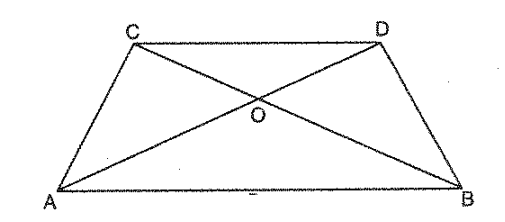
View SolutionGiven below is a parallelogram `A B C Ddot\ ` Complete each statement along with the definition or property used.
(i)`A D=`
(ii) `/_D C B=`
(iii)`O C=`
(iv) `/_D A B+/_C D A=`
View SolutionThe following figures are parallelograms. Find the degree values of the unknowns `x ,\ y ,\ z`
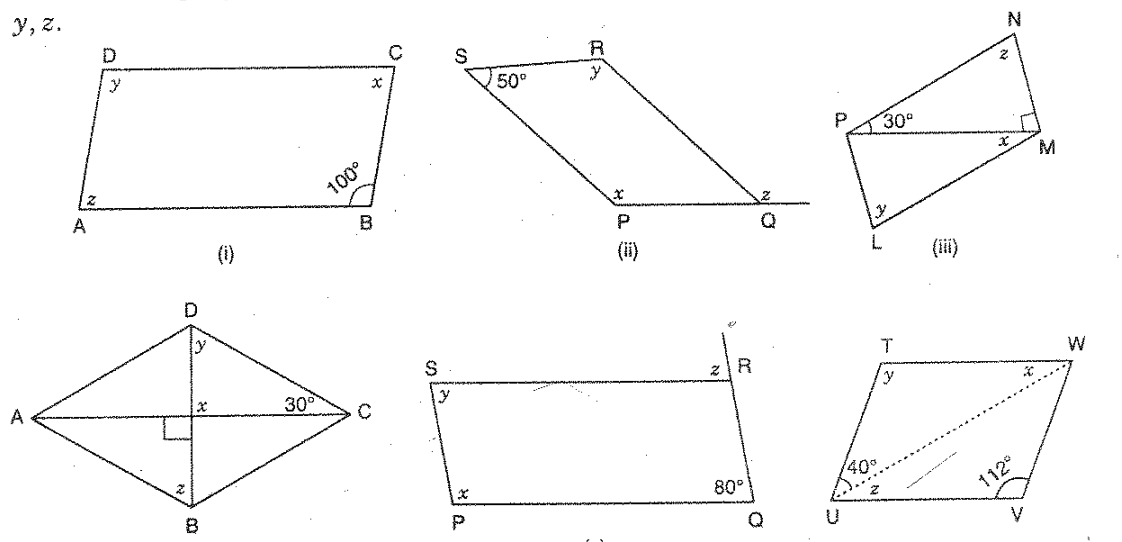
View SolutionCan the following figures be parallelograms. Justify your answer.

View SolutionIn the adjacent figure `H O P E` is a parallelogram. Find the angle measures `x ,\ y\ a n d\ Zdot` State the geometrical truths you use to find them.
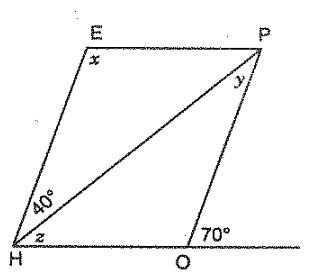
View SolutionIn the following figures `G U N S\ a n d\ R U N S` are parallelograms. FinD `x\ a n d\ y` .
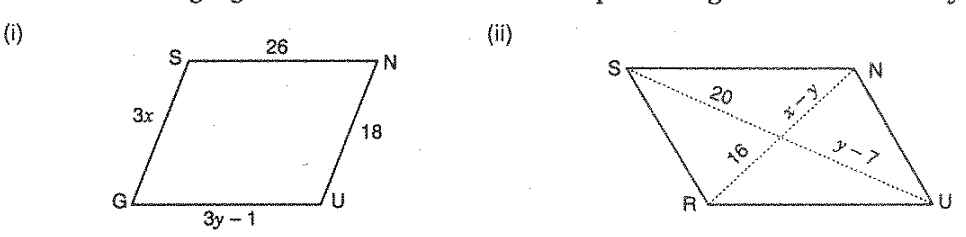
View SolutionIn the following figures `R I S K\ a n d\ C L U E` are parallelograms. Find the measure of `xdot`
View SolutionTwo opposite angles of a parallelogram are `(3x-2)^@ a n d\ \ (50-x)^@dot` Find the measure of each angle of the parallelogram.
View SolutionIf an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
View SolutionThe measure of one angle of a parallelogram is `70^0dot` What are the measures of the remaining angles?
View SolutionTwo adjacent angles of a parallelogram are as 1:2. Find the measures of all the angles of the parallelogram.
View SolutionIn a parallelogram `A B C D ,\ /_D=135^0,` determine the measure of `/_A\ a n d\ /_Bdot`
View Solution`A B C D` is a parallelogram in which `/_A=70^@dot` Compute `/_B ,\ /_C\ a n d\ /_Ddot`
View SolutionThe sum of two opposite angles of a parallelogram is `130^@dot` Find all the angles of the parallelogram.
View SolutionAll the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
View SolutionTwo adjacent sides of a parallelogram is 150cm. One of its sides is greater than the other by 25cm. Find the length of the sides of the parallelogram.
View SolutionThe perimeter of a parallelogram is 150cm. One of its sides is greater than the other by 25cm. Find the length of the sides of the parallelogram.
View SolutionThe shorter side of a parallelogram is 4.8cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
View SolutionTwo adjacent angles of a parallelogram are `(3x-4)^@a n d\ (3x+10)^@dot` Find the angles of the parallelogram.
View SolutionIn a parallelogram `A B C D ,` the diagonals bisect each other at `Odot` If `/_A B C=30^0,\ /_B D C=10^0a n d\ /_C A B=70^0,` Find: `/_D A B ,\ /_A D C ,\ /_B C D ,\ /_A O D ,\ /_D O C ,\ /_B O C ,\ /_A O B ,\ ` `/_A C D ,\ /_C A B ,\ /_A D B`
Given that
` ∠ABC = 30^2, ∠ABC = ∠ADC = 30^0`
[We know that measure of opposite angles are equal in a parallelogram]
`∠BDC = 10^0`
`∠CAB =70^0`
`∠BDA = ∠ADB = ∠ADC – ∠BDC `
` 30^2 – 10^2 = 20^2`
`∠DAB = 180^0 – 30^0 = 150^0`
` ∠ADB = ∠DBC = 20^0` (alternate angles)
` ∠BCD = ∠DAB = 150^0`
[we know, opposite angles are equal in a parallelogram]
` ∠DBA = ∠BDC = 10^0`
[we know, Alternate interior angles are equal]
In` ΔABC`
`∠CAB + ∠ABC + ∠BCA = 180^0`
[since, sum of all angles of a triangle is 180^0]
`70^0 + 30^0 + ∠BCA = 180^0`
`∠BCA = 180^0 – 100^0 = 80^0`
` ∠DAB = ∠DAC + ∠CAB = 70^0 + 80^0 = 150^0 `
`∠BCD = 150^0` (opposite angle of the parallelogram)
` ∠DCA = ∠CAB = 70^0 `
In `ΔDOC ∠BDC + ∠ACD + ∠DOC = 180^0`
[since, sum of all angles of a triangle is 180^0]
`10^0 + 70^0 + ∠DOC = 180^0 `
`∠DOC = 180^0- 80^0`
`∠ACB = 80^0`
View SolutionFind the angles marked with a question mark shown in Figure:

View SolutionThe angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is `60^0dot` Find the angles of parallelogram.
View SolutionIn Figure, `A B C D\ a n d\ A E F G` are parallelograms. If `/_C=55^0,` what is the measure of `/_F ?`
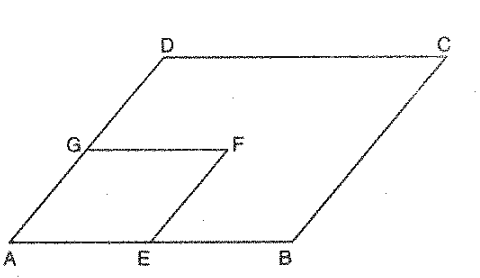
View SolutionIn Figure, `B D E F\ a n d\ D C E F` are each a parallelogram. Is it true that `B D=D C ?` Why or why not?
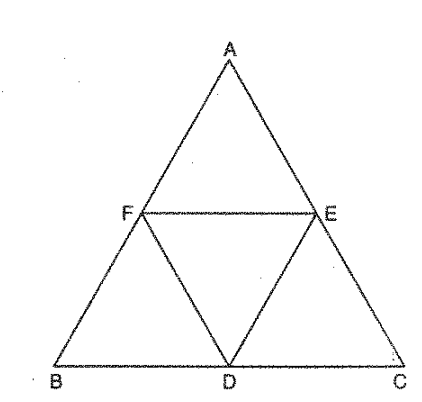
View SolutionIn Figure, suppose it is known that `D E=D Fdot` Then, is ` A B C` isosceles? Why or why not?
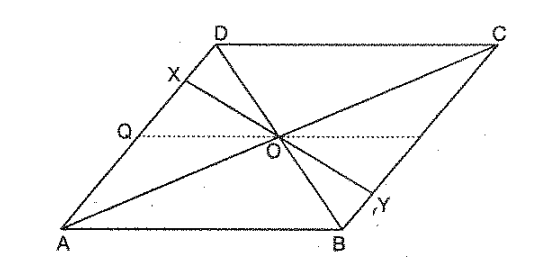
View SolutionDiagonals of parallelogram `A B C D` intersect at `O` as shown in Figure. XY contains `O ,\ a n d\ X ,\ Y` are points on opposite sides of the parallelogram. Give reasons for each of the following: `O B=O D` (ii) `/_O B Y=/_O D X` `/_B O Y=\ /_D O X` (iv) ` B O Y~= D O X` Now, state if `X Y` is bisected at `Odot`
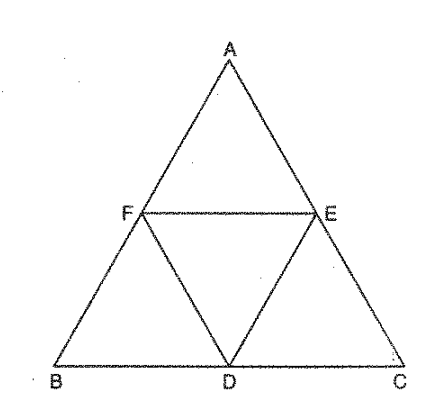
View SolutionIn Figure, `A B C D` is a parallelogram, `C E` besects `/_C\ a n d\ A F` bisects `/_Adot` In each of the following, if the statement is true, give a reason for the same: `/_A=/_C` (ii) `/_F A B=1/2/_A` `/_D C E=1/2/_C` (iv) `/_C E B=/_F A B` `c e A F`
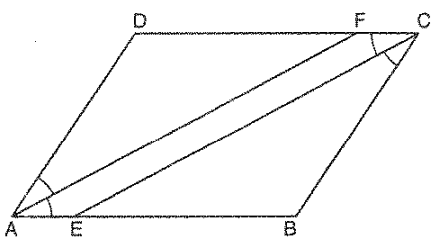
View SolutionDiagonals of a parallelogram `A B C D` intersect at `OdotA L\ a n d\ C M` are perpendiculars to `B D` such that `L\ a n d\ M` lie on `B D` . IS `A L=C M ?` why or why not?
View SolutionPoint `E\ a n d\ F` lie on diagonals `A C` of a parallelogram `A B C D` such that `An E=C Fdot` What type of quadrilateral is `B F D E ?` From the given figure we see that `BFDE`is also a parallelogram.
View SolutionIn a parallelogram `A B C D ,\ A B=10 c m ,\ A D=6c mdot` The bisector of `/_A` meets `D C` in `E,\ A E\ a n d\ B C` produced meet at `Fdot` Find the length `C Foot
View SolutionIn Figure, `R I C E` is parallelogram. Find `x ,\ y ,\ zdot`

View SolutionIn Figure, `A B C D` is a rhombus with `/_A B C=56^0dot` Determine `/_A C Ddot`
View SolutionOne of the diagonals of a rhombus is equal to one of its sides. Find the angles of the rhombus.
View Solution`A B C D` is a rhombus in which the altitude from `D` to side `A B\ ` bisects `A Bdot` Find the angles of the rhombus.
View SolutionConstruct a rhombus whose diagonals are 10cm and 8cm.
View SolutionWhich of the following statements are true for a rhombus?
View SolutionFill in the blanks, in each of the following, so as to make the statement true: (i)A rhombus is a parallelogram in which.... (ii)A square is a rhombus in which.... (iii)A rhombus has all its sides of ........ length. (iv)The diagonals of a rhombus..... each other at... angles. (v)If the diagonals of a parallelogram bisect each other at right angles, then it is a....
View SolutionThe diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
View SolutionThe diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is ‘No’, draw a figure to justify your answer.
View Solution`A B C D` is a rhombus. If `/_A C B=40^@,` find `/_A D Bdot`
View SolutionIf the diagonals of a rhombus are 12cm and 16cm, find the length of each side.
View SolutionConstruct a rhombus whose diagonals are of length 10cm and 6cm.
View SolutionDraw a rhombus, having each side of length 3.5cm and one of the angle as `40^0dot`
View SolutionOne side of a rhombus is a length of 4cm and the length of an altitude is 3.2cm. Draw the rhombus.
View SolutionDraw a rhombus, having each side of length 3.5cm and one of the angle as `40^0dot`
View SolutionOne side of a rhombus is of length 4cm and the length of an altitude is 3.2cm. Draw the rhombus.
View SolutionDraw a rhombus `A B C D ,` if `A B=6c m\ a n d\ A C=5c mdot`
View Solution`A B C D` is a rhombus and its diagonals intersect at `Odot`
Is ` B O C\ ~= D O C ?` State the congruence condition used?
Also state, if ` B C O= D C O`
View SolutionShow that each diagonal of a rhombus bisects the angle through which it passes. Let ABCD be a rhombus whose diagonal AC and BD intersect each other at O.
In `triangle AOD and triangle AOB`
`AD=AB`(sides of rhombus are equal)
`AO=AO`(common side)
`DO=OB`(diagonals bisect each other)
`triangle AOD cong triangle AOB`
`angleDAO=angle BAO`(cpct)
`angle ABO=angle CBO `
`angleADO =angle CDO `
Hence proved
View Solution`A B C D` is a rhombus whose diagonals intersect at `Odot` If `A B=10 c m,` diagonals `B D=16\ c m` , find the length of diagonal `A C`
View Solution
View SolutionIn Figure, `R E N T` is a rectangle. Its diagonals meet at `Odot` Find `x,` if `O R=2x+4\ a n d\ O T=3x+1.`
View Solution`P Q R S` is a square. `P R` and `S Q` intersect at `Odot` State the measure of `/_P O Qdot`
View SolutionIn Figure, `P Q R S` is a square. Determine `/_S R Pdot`
View Solution`A B C D` is a rectangle with `/_B A C=32^0dot` Determine `/_D B Cdot`
View SolutionThe diagonals of a rectangle `A B C D` meet at `Odot` If `/_B O C=44^@,` find `/_O A Ddot`
View SolutionIn Figure, `A B C D` is a rectangle. `B M\ a n d\ D N` are perpendicular from `B\ a n d\ D` respectively on `A C` . Prove that ` M B Ccong D N A` (ii) `B M=D N`
View SolutionThe diagonals of a rectangle `A B C D` intersect in `Odot` If `/_B O C=68^0,` find `/_O D Adot`
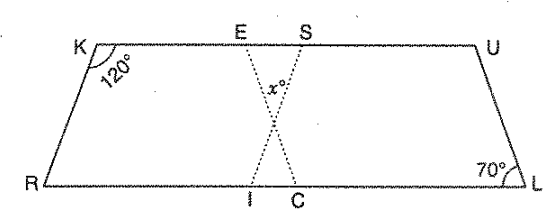
View SolutionExplain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
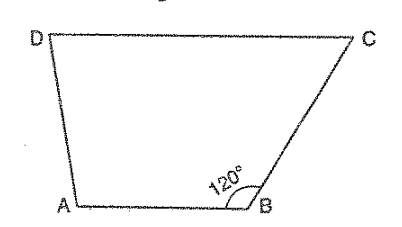
View SolutionIn the following figure `A B C D` is a trapezium in which `A B D Cdot` Find the measure of `/_C` .
View SolutionThe adjacent figure `P Q R S` is a trapezium in which `S P || R Q ,` find the measures of `/_P\ a n d\ /_Rdot`
View SolutionWhich of the following statements are true for a rectangle? It has two pairs of equal sides. It has all its sides of equal length. Its diagonals are equal. Its diagonals bisect each other. Its diagonals are perpendicular. Its diagonals are perpendicular and bisect each other. Its diagonals are equal and bisect each other. Its diagonals are equal and perpendicular, and bisect each other. All rectangles are squares. All rhombuses are parallelograms. All squares are rhombuses and also rectangles. All squares are not parallelograms. A rectangle is a parallelogram with one of its angles equal to right angles.
View SolutionWhich of the following statements are true for a square? It is a rectangle. It has all its sides of equal length. Its diagonals bisect each other at a right angle. Its diagonals are equal to its sides.
View SolutionFill in the blanks in each of the following, so as to make the statement true: A rectangle is a parallelogram in which.... A square is a rhombus in which.... A square is a rectangle is which....
View SolutionA window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
View SolutionIn a rectangle `A B C D ,` prove that ` A C Bcong C A Ddot`
View SolutionThe sides of a rectangle are in the ratio 2:3, and its perimeter is 20cm. Draw the rectangle.
View SolutionThe sides of a rectangle are in the 4:5. Find its sides if the perimeter is 90cm.
View SolutionWhat is the length of a diagonal of a rectangle whose sides are 5 cm and 12 cm long?
View SolutionConstruct a rectangle of side 8cm and diagonal 10 cm.
View SolutionConstruct a square of side 4.8 cm.
View SolutionIdentify all the quadrilaterals that have: (a) four sides of equal length (b) four right angles
View SolutionQ3) Explain how a square is: (a) a quadrilateral (b) a parallelogram (c) a rhombus (d) a rectangle
View SolutionName the quadrilaterals whose diagonals (i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
View SolutionABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
View SolutionTo make a concrete rectangular slab the man should ensure?.
View Solution
All Questions questions and complete solutions for chapter UNDERSTANDING PHASE-III (SPECIAL TYPES OF QUADRILATERALS) of RD SHARMA MATHS (HINGLISH) of Class 8