Complete Solutions to Exercise 11.4 of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| CPC CAMBRIDGE PUBLICATION | Exercise 11.4 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Parallelogram ABCD and rectangle ABEF are on the base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn the following Figure, D and E are two points on BC such that BD = DE = EC . Show that ar (ABD) = ar (ADE) = ar(AEC)
can you now answer the equation that you left in the "Introduction " of the capther, whether the filed of Budhia has been actually divided into three parts of equal area ?
View SolutionIn the following figure, ABCD, DCFR and ABFE are parallelograms. Show that ar (ADE) = ar (BCF)
View SolutionIn the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect AD = CQ. If AQ intersect DC at P, Show that ar (BPC) = ar (DPQ)
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8` ar(AFC)
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) ` xx ` ar (CPD) =ar (APD) `xx` ar (BPC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid point at AP, show that
(i) ar (PQR) = ` 1/2` ar (ARC)
(ii) ar (RQC) = `3/8` ar (ABC)
(iii) ar (PBQ) = ar (ARC)
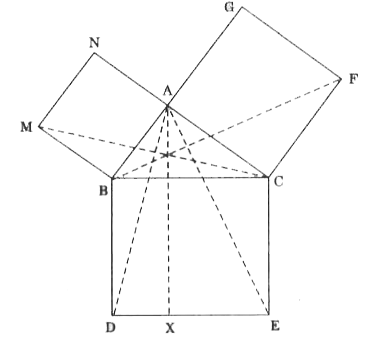
View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ` bot ` DE meets BC at Y. Show that
(i) ` tirangle MBC = tirangle (MBC)`
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ` tirangle FCB = tirangle ACE`
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
View Solution
Exercise 11.4 questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9