Complete Solutions to TOPIC-2 of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| OSWAL | TOPIC-2 |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
`angleBOC`
View SolutionIn the given on equilateral triangle ABC is inscribed in a ciecle with centre O. Find:
`angle OBC` and `angle BOC`
View SolutionIn the given the length of arcs AB and BC are in the ratio `3:2.`
If `angle AOB = 96 ^(@)` find
`angle BOC`
View SolutionIn the given the length of arcs AB and BC are in the ratio `3:2.`
If `angle AOB = 96 ^(@)` find
` angle ABC`
View SolutionDraw the circles of different radii. How many points, these circles can have in common ? What is the maximum number of common points ?
View SolutionSuppose you are given a circle. Describe a method by which you can find the centre of this circle.
View SolutionThe circumference of a circle, with centre O, is divided into three arcs APB, BQC and CRA such that : `(arc APB)/(2)= (arc BQC)/(3) =(arc CRA)/(4)` Find `angleBOC`.
View SolutionIn the given arc AB= twice are BC and `angle AOB = 80 ^(@)` find:
`angle BOC`
View SolutionIn the given arc AB= twice are BC and `angle AOB = 80 ^(@)` find:
`angle OAC`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.
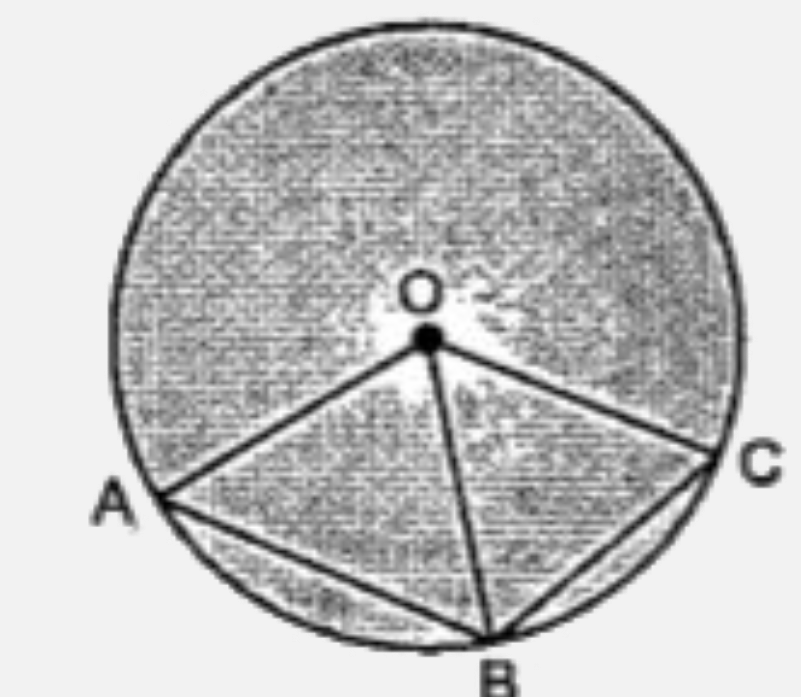
`angle AOB`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.
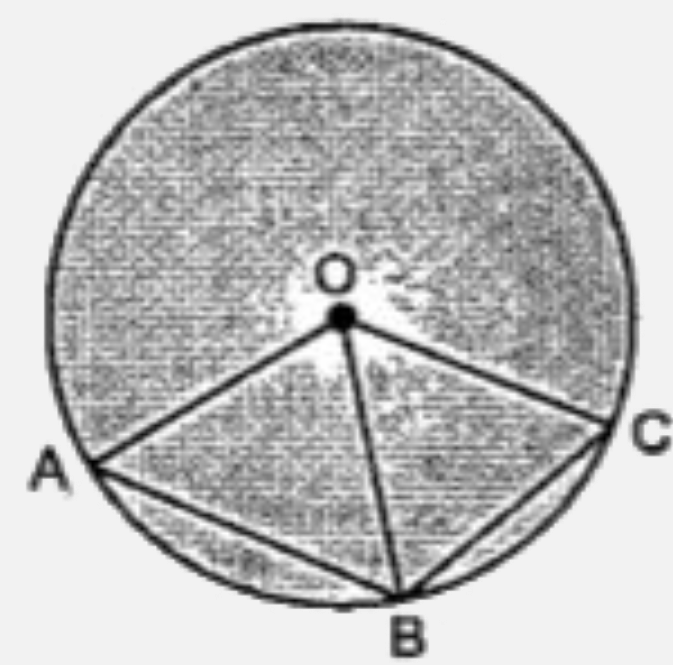
`angle BOC`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

`angle AOC`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

`angle OBA`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

`angle OBC`
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

`angle ABC`
View SolutionIn the given `AB= BC = DC and angle AOB = 50^(@)`
`angle AOC`
View SolutionIn the given `AB= BC = DC and angle AOB = 50^(@)`
`angle AOD`
View SolutionIn the given `AB= BC = DC and angle AOB = 50^(@)`
` angle BOD`
View SolutionIn the given figure, AB = BC = DC and `angleAOB = 50^(@)`

`angleOAC`
View SolutionIn the given figure, AB = BC = DC and `angleAOB = 50^(@)`

`angleODA`
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and `anglePOQ = 150^(@)` find `angleAPQ
View SolutionIn the given figure, 'O' is the centre of the circle, Arc AB = Arc BC = Arc CD. If `angle OAB = 48^(@)`, find :

(i) `angle AOB`
(ii) `angle BOD`
View SolutionIn the given figure, 'O' is the centre of the circle, Arc AB = Arc BC = Arc CD. If `angle OAB = 48^(@)`, find :

(i) `angle AOB`
(ii) `angle BOD`
View SolutionIn the given 'O' is the centre of the circle, Arc `AB = Arc BC = Cd. If angle OAB = 48 ^(@),` find:
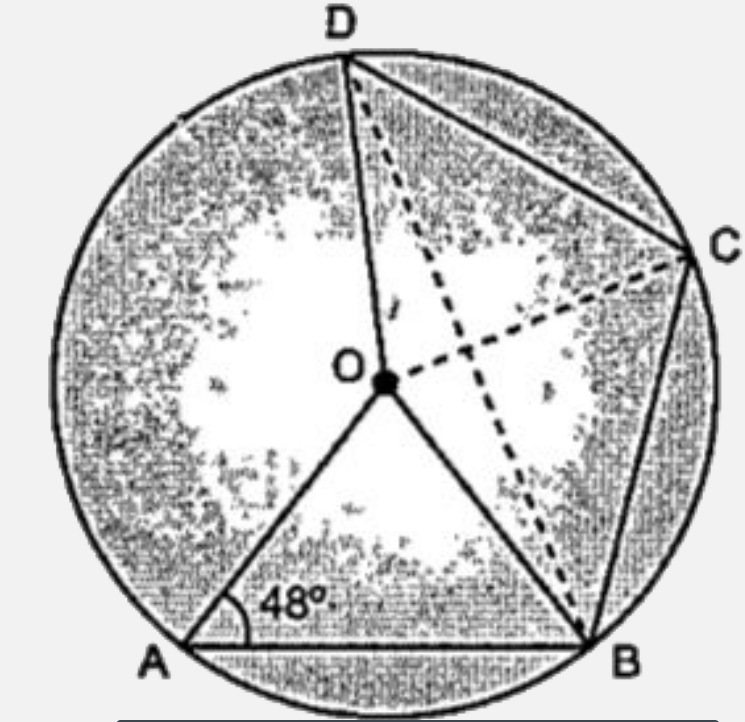
` angle OBD`
View Solution
TOPIC-2 questions and complete solutions for chapter CIRCLES of ICSE of Class 9