Complete Solutions to Exercies 16(C ) of chapter AREA THEOREMS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA THEOREMS |
| SELINA PUBLICATION | Exercies 16(C ) |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
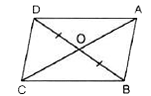
In the given figure, the diagonals AC and BD intersects at point O. If OB=OD and `AB////DC`, prove that :
(i) ` "Area" (DeltaDOC)= "Area" (DeltaAOB)`.
(ii) ` "Area" (DeltaDCB)= "Area" (DeltaACB)`.
(iii) ABCD is a parallelogram.
View SolutionThe given figure shows a parallelogram ABCD with area `324sq.` cm. P is a point in AB such that AP:PB= `1:2`. Find the area of `DeltaAPD`.
View SolutionIn `triangleABC`,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the `DeltaOBC` and quadrilateral AEOF are equal in area.
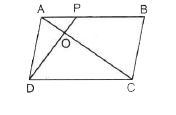
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of `DeltaPOB=40cm^(2)` and OP:OC= `1:2`, find :
(i) Areas of `DeltaBOC` and `DeltaPBC`
(ii) Areas of `DeltaABC` and parallelogram ABCD.
View SolutionThe medians of a triangle ABC intersect each other at point G. If one of its medians is AD, Prove that :
(i) ` "Area (ΔABD)=3x "Area" (ΔBGD)`
(ii) ` "Area (ΔACD)=3x "Area" (ΔCGD)`
(iii) ` "Area (ΔBGC)=(1)/(3)x "Area" (ΔABC)`
View SolutionThe perimeter of a triangle is `300 mdot` If its sides are in the ratio `3:5: 7.` Find the area of the triangle.
View SolutionIn parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF:FE= `5:3` and area of `DeltaADF` is `60cm^(2)`, find :
(i) area of `DeltaADE`
(ii) if AE:EB= `4:5`, find the area of `DeltaADB`
(iii) also, find area of parallelogram ABCD.
View SolutionIn the following figure, BD is parallel to CA, E is mid-point of CA and BD = `(1)/(2)` CA.
Prove that : `ar.(DeltaABC)=2xxar.(DeltaDBC)`
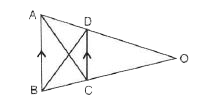
View SolutionIn the following figure, OAB is a triangle and `AB////DC`.
If the area of `DeltaCAD=140cm^(2)` and the area of `DeltaODC=172cm^(2)`, find
(i) the area of `DeltaDBC`
(ii) the area of `DeltaOAC`
(iii) the area of `DeltaODB`.
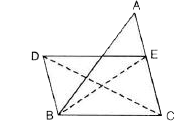
View SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of `DeltaADX` = area of `DeltaACY`.
View SolutionIn the given figure, the diagonals AC and BD intersects at point O. If OB=OD and `AB////DC`, prove that :
(i) ` "Area" (DeltaDOC)= "Area" (DeltaAOB)`.
(ii) ` "Area" (DeltaDCB)= "Area" (DeltaACB)`.
(iii) ABCD is a parallelogram.

View SolutionThe given figure shows a parallelogram ABCD with area `324sq.` cm. P is a point in AB such that AP:PB= `1:2`. Find the area of `DeltaAPD`.

View SolutionIn `triangleABC`,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the `DeltaOBC` and quadrilateral AEOF are equal in area.
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of `DeltaPOB=40cm^(2)` and OP:OC= `1:2`, find :
(i) Areas of `DeltaBOC` and `DeltaPBC`
(ii) Areas of `DeltaABC` and parallelogram ABCD.
View SolutionThe medians of a triangle ABC intersect each other at point G. If one of its medians is AD, Prove that :
(i) ` "Area (ΔABD)=3x "Area" (ΔBGD)`
(ii) ` "Area (ΔACD)=3x "Area" (ΔCGD)`
(iii) ` "Area (ΔBGC)=(1)/(3)x "Area" (ΔABC)`
View SolutionThe perimeter of a triangle ABC is `37` cm and the ratio between the lengths of its altitudes be `6:5:4`. Find the lengths of its sides.
View SolutionIn parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF:FE= `5:3` and area of `DeltaADF` is `60cm^(2)`, find :
(i) area of `DeltaADE`
(ii) if AE:EB= `4:5`, find the area of `DeltaADB`
(iii) also, find area of parallelogram ABCD.
View SolutionIn the following figure, BD is parallel to CA, E is mid-point of CA and BD = `(1)/(2)` CA.
Prove that : `ar.(DeltaABC)=2xxar.(DeltaDBC)`

View SolutionIn the following figure, OAB is a triangle and `AB////DC`.
If the area of `DeltaCAD=140cm^(2)` and the area of `DeltaODC=172cm^(2)`, find
(i) the area of `DeltaDBC`
(ii) the area of `DeltaOAC`
(iii) the area of `DeltaODB`.

View SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of `DeltaADX` = area of `DeltaACY`.
View Solution
Exercies 16(C ) questions and complete solutions for chapter AREA THEOREMS of ICSE of Class 9