Complete Solutions to Example of chapter AREA THEOREMS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA THEOREMS |
| SELINA PUBLICATION | Example |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
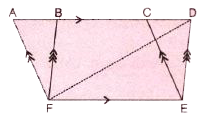
In the adjoining figure, area of parallelogram AFEC is `140cm^(2)`. State, giving reason, the area of :
(i) parallelogram BFED.
(ii) triangle BFD.
View SolutionIn a given figure, `AB////DC////EF, AD////BE "and" DE////AF`. Prove that the area of prallelogram DEFH is equal to the area of parallelogram ABCD.

View SolutionP is any point inside a parallelogram ABCD. Prove that :
Area `(DeltaAPB)+Area(DeltaCPD)`
`=Area(DeltaAPD)+Area(DeltaBPC)`
View SolutionProve that a median divides a triangle into two triangles of equal area.
View SolutionIn `DeltaABC`, AD divides BC in thr ratio `m:n`. Show that `( "Area" (DeltaABD))/( "Area" (DeltaADC))=(m)/(n)`
View SolutionIn triangle ABC, D is a point in side BC such that `2BD=3DC`. Prove that the area of triangle ABD = `(3)/(5)xx "Area of" DeltaABC`
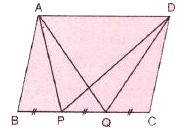
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
`ar.(DeltaAPQ)=ar.(DeltaDPQ)`
`=(1)/(6)xxar.` (Parallelogram ABCD)
View SolutionIn the adjoining figure, area of parallelogram AFEC is `140cm^(2)`. State, giving reason, the area of :
(i) parallelogram BFED.
(ii) triangle BFD.

View SolutionIn a given figure, `AB////DC////EF, AD////BE "and" DE////AF`. Prove that the area of prallelogram DEFH is equal to the area of parallelogram ABCD.

View SolutionP is any point inside a parallelogram ABCD. Prove that :
Area `(DeltaAPB)+Area(DeltaCPD)`
`=Area(DeltaAPD)+Area(DeltaBPC)`
View SolutionProve that a median divides a triangle into two triangles of equal area.
View SolutionIn `DeltaABC`, AD divides BC in thr ratio `m:n`. Show that `( "Area" (DeltaABD))/( "Area" (DeltaADC))=(m)/(n)`
View SolutionIn triangle ABC, D is a point in side BC such that `2BD=3DC`. Prove that the area of triangle ABD = `(3)/(5)xx "Area of" DeltaABC`
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
`ar.(DeltaAPQ)=ar.(DeltaDPQ)`
`=(1)/(6)xxar.` (Parallelogram ABCD)

View SolutionThe area of the sector of a circle with radius 6 cm and of angle `60^@` is
View Solution
Example questions and complete solutions for chapter AREA THEOREMS of ICSE of Class 9