Complete Solutions to Exercies 16(B) of chapter AREA THEOREMS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA THEOREMS |
| SELINA PUBLICATION | Exercies 16(B) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
Show that :
(i) a diagonal divides a parallelogram into two triangles of equal area.
(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
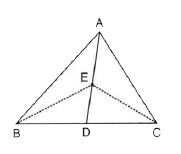
View SolutionIn the given figure, AD is median of `DeltaABC` and E is any point on median AD. Prove that Area `(DeltaABE)` = Area `(DeltaACE)`
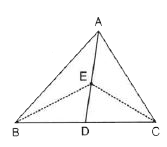
View SolutionIn the figure of question `2`, if E is the mid point of median AD, then prove that :
`"Area" (DeltaABE)=(1)/(4) "Area" (DeltaABC)`.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= `(1)/(8)` of the area of parallelogram ABCD.
View SolutionThe base BC of triangle ABC is divided at D so that BD = `(1)/(2)` DC.
Prove that area of `DeltaABD=(1)/(3)` of the area of `DeltaABC`.`
View SolutionIn a parallelogram ABCD, point P lies in DC such that DP:PC= `3:2`. If area of `DeltaDPB=30sq.` cm, ffind the area of the parallelogram ABCD.
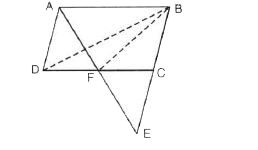
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If `ar.(DeltaDFB)=30cm^(2)`, find the area of parallelogram
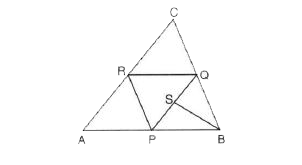
View SolutionThe following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : `ar.(DeltaABC)=8xxar.(DeltaQSB)`
View SolutionShow that :
(i) a diagonal divides a parallelogram into two triangles of equal area.
(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
View SolutionIn the given figure, AD is median of `DeltaABC` and E is any point on median AD. Prove that Area `(DeltaABE)` = Area `(DeltaACE)`

View SolutionIn the figure of question `2`, if E is the mid point of median AD, then prove that :
`"Area" (DeltaABE)=(1)/(4) "Area" (DeltaABC)`.

View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= `(1)/(8)` of the area of parallelogram ABCD.
View SolutionThe base BC of triangle ABC is divided at D so that BD = `(1)/(2)` DC.
Prove that area of `DeltaABD=(1)/(3)` of the area of `DeltaABC`.`
View SolutionIn a parallelogram ABCD, point P lies in DC such that DP:PC= `3:2`. If area of `DeltaDPB=30sq.` cm, ffind the area of the parallelogram ABCD.
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If `ar.(DeltaDFB)=30cm^(2)`, find the area of parallelogram

View SolutionThe following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : `ar.(DeltaABC)=8xxar.(DeltaQSB)`

View Solution
Exercies 16(B) questions and complete solutions for chapter AREA THEOREMS of ICSE of Class 9