Complete Solutions to Exercies 16(A) of chapter AREA THEOREMS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA THEOREMS |
| SELINA PUBLICATION | Exercies 16(A) |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
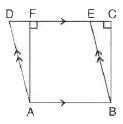
In the given figure, if area of triangle ADE is `60cm^(@)`, giving reason, the area of :
(i) parallelogram ABED,
(ii) rectangle ABCF,
(iii) triangle ABE.
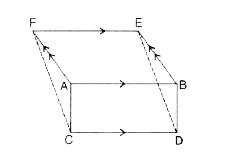
View SolutionThe given figure shows a rectangle ABDC and a parallelogram ABEF, drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram, (ii) Area of quad. CDEF
= Area of rec. ABDC
`+ "Area of" ////gm.ABEF`.
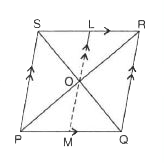
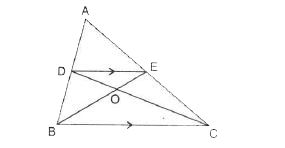
View SolutionIn the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) `2 "Area" (DeltaPOS)= "Area" (////gmPMLS)`
(ii) `"Area" (DeltaPOS)+ "Area" (DeltaQOR)`
`=(1)/(2) "Area" (////gmPQRS)`
(iii) `"Area" (DeltaPOS)+ "Area" (DeltaQOR)`
`= "Area" (DeltaPOQ)+ "Area" (tDeltaSOR)`
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) `DeltaCPD` and `DeltaAQD` are equal in area.
(ii) Area `(DeltaAQD)`
`= "Area" (DeltaAPD)+ "Area" (DeltaCPB)`
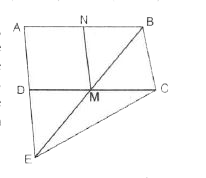
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is `48cm^(2)`,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
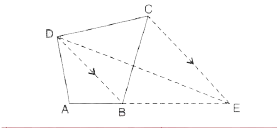
View SolutionIn the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced ar point E.
Prove that `DeltaADE` and quadrilateral ABCD are equal in area.
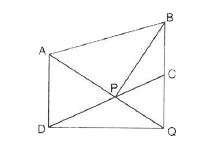
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.
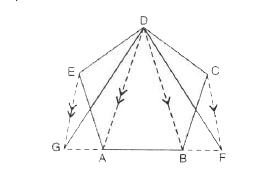
View SolutionThe given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
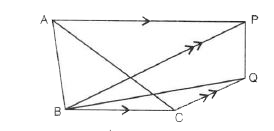
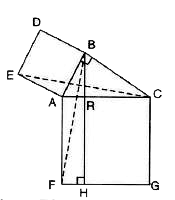
View SolutionIn the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) `DeltaEAC~=DeltaBAF`.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) ` "Area" (DeltaADC)= "Area" (DeltaAEB)`
(ii) ` "Area" (DeltaBOD)= "Area" (DeltaCOE)`.
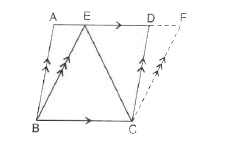
View SolutionABCD and BCFE are parallelograms. If area of triangle `EBC=480cm^(2), AB=30cm "and" BC=40cm`, Calculate,
(i) area of parallelogram ABCD,
(ii) area of the parallelogram BCFE,
(iii) length of altitude from A on CD,
(iv) area of triangle ECF.
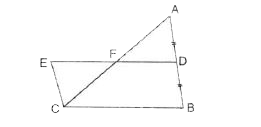
View SolutionIn the given figure, D is mid-point of side AB of `triangleABC` and BDEC is a parallelogram.
Prove that :
Area of `DeltaABC` = Area of `////gmBDEC`
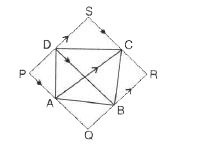
View SolutionIn the following figure, `AC////PS////QR "and" PQ////DB////SR`.
Prove that :
Area of quadrilateral `PQRS=2xx "Area of quad. ABCD"`.
View SolutionABCD is a trapezium with `AB////DC`. A line parallel to AC intersects Ab at point M and BC at point N. Prove that :
`"area of" DeltaADM= "area of" DeltaACN`.
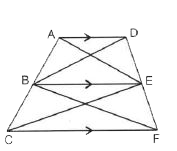
View SolutionIn the given figure, `AD////BE////CF`.
prove that :
area `(DeltaAEC)`
= area `(DeltaDBF)`
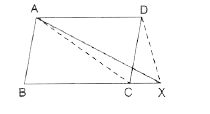
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
`"area" (DeltaABX)= "area" (quad.ACXD)`
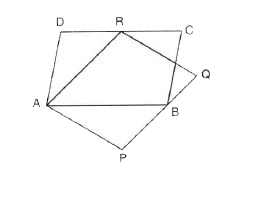
View SolutionThe given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
[Join B and R]
View SolutionIn the given figure, if area of triangle ADE is `60cm^(@)`, giving reason, the area of :
(i) parallelogram ABED,
(ii) rectangle ABCF,
(iii) triangle ABE.

View SolutionThe given figure shows a rectangle ABDC and a parallelogram ABEF, drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram, (ii) Area of quad. CDEF
= Area of rec. ABDC
`+ "Area of" ////gm.ABEF`.

View SolutionIn the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) `2 "Area" (DeltaPOS)= "Area" (////gmPMLS)`
(ii) `"Area" (DeltaPOS)+ "Area" (DeltaQOR)`
`=(1)/(2) "Area" (////gmPQRS)`
(iii) `"Area" (DeltaPOS)+ "Area" (DeltaQOR)`
`= "Area" (DeltaPOQ)+ "Area" (tDeltaSOR)`

View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) `DeltaCPD` and `DeltaAQD` are equal in area.
(ii) Area `(DeltaAQD)`
`= "Area" (DeltaAPD)+ "Area" (DeltaCPB)`
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is `48cm^(2)`,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.

View SolutionIn the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced ar point E.
Prove that `DeltaADE` and quadrilateral ABCD are equal in area.

View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.

View SolutionThe given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.

View SolutionIn the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) `DeltaEAC~=DeltaBAF`.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.

View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) ` "Area" (DeltaADC)= "Area" (DeltaAEB)`
(ii) ` "Area" (DeltaBOD)= "Area" (DeltaCOE)`.

View SolutionABCD and BCFE are parallelograms. If area of triangle `EBC=480cm^(2), AB=30cm "and" BC=40cm`, Calculate,
(i) area of parallelogram ABCD,
(ii) area of the parallelogram BCFE,
(iii) length of altitude from A on CD,
(iv) area of triangle ECF.

View SolutionIn the given figure, D is mid-point of side AB of `triangleABC` and BDEC is a parallelogram.
Prove that :
Area of `DeltaABC` = Area of `////gmBDEC`

View SolutionIn the following figure, `AC////PS////QR "and" PQ////DB////SR`.
Prove that :
Area of quadrilateral `PQRS=2xx "Area of quad. ABCD"`.

View SolutionABCD is a trapezium with `AB////DC`. A line parallel to AC intersects Ab at point M and BC at point N. Prove that :
`"area of" DeltaADM= "area of" DeltaACN`.
View SolutionIn the given figure, `AD////BE////CF`.
prove that :
area `(DeltaAEC)`
= area `(DeltaDBF)`

View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
`"area" (DeltaABX)= "area" (quad.ACXD)`

View SolutionThe given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
[Join B and R]

View Solution
Exercies 16(A) questions and complete solutions for chapter AREA THEOREMS of ICSE of Class 9