Complete Solutions to EXERCISE 7.1 of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| KUMAR PRAKASHAN | EXERCISE 7.1 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
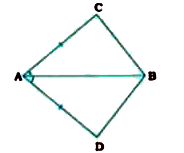
In quadrilateral ACBD. AC = AD and AB bisects `angle` A (see the given figure). Show that `triangle ABC = triangle ABD`. What can you say about BC and BD?
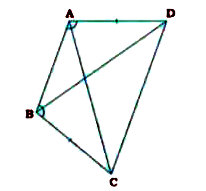
View SolutionABCD is a quadrilateral in which AD = BC and `angle DAB = angle CBA` (see the given figure). Prove that ( i ) `triangle ABD = triangle BAC, ( ii) BD = AC and (iii) angle ABD = angle BAC`
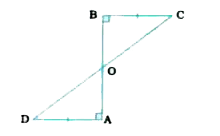
View SolutionAD and BC are equal perpendiculars to a line segment AB (see the given figure) Show that CD bisects AB.
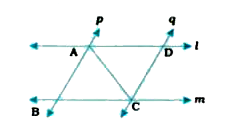
View SolutionI and m are two parallel lines intersected by another pair of parallel lines p and show that `triangle ABC = triangle CDA`
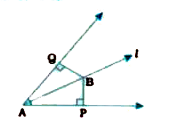
View SolutionRay 1 is the bisector of an angle `angle` A and B is any point on I. BP and BQ are perpendiculars from B to the arms of `angle` A (see the given figure). Show that:
(i) `triangleAPB=triangleAQB`
(ii) BP = BQ or B is equidistant from the arms of `angleA`
View SolutionIn the given figure, AC = AE, AB = AD and `angle BAD = angle EAC`. Show that BC = DE.

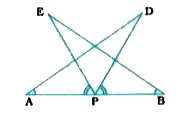
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angle BAD = angle ABE and angle EPA = angle DPB` (see the given figure). Show that:
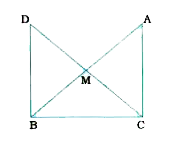
View SolutionIn right triangle ABC, right angled at C, M is the midpoint of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
(i) `triangle AMC = triangleBMD`
(ii) `angle DBC` is a right angle
(iii) `triangleDBC = triangleACB`
(iv) `CM=1/2` AB
`
View Solution
EXERCISE 7.1 questions and complete solutions for chapter TRIANGLES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9