Complete Solutions to SKILL TESTING EXERCISE of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| KUMAR PRAKASHAN | SKILL TESTING EXERCISE |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
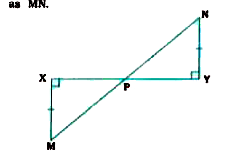
In the given figure, XM and YN are both `lt` perpendicular to line segment XY and XM = YN. 4 Prove that P is the midpoint of XY as well as MN
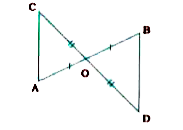
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
View SolutionIn rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View SolutionProve that the medians of an equilateral triangle are equal.
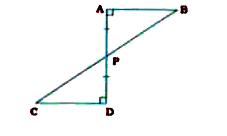
View SolutionIn the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.
View SolutionIn `triangle` ABC, AB = AC and the bisector of `angle A lt` intersects BC at D. Prove that, ( 1 )`triangle ADB = triangle ADC ( 2 ) angle ABC = angle ACB`
View SolutionIn `triangle` ABC, the bisectors of `angle`B and `angle` C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionIn `triangle` ABC, AB = AC and `angle` A = `36^(@)`. The bisector of `angle` C intersects AB at D. Find the measures of required angles to prove that AD = BC
View SolutionIn the given figure, PS = PR and `angle` TPS = `angle` QPR. Prove that PT = PQ.

View SolutionIn `triangle` ABC, D is the midpoint of BC. DFZAB and DE `bot` AC, where points F and E lie on AB and AC respectively. If DF = DE, prove that A ABC is an isosceles triangle.
View SolutionIn parallelogram ABCD, diagonals AC and BD are equal. Find the measure of `angle` ABC and prove that the quadrilateral ABCD is a rectangle.
View Solution`triangle` ABC and `triangle` DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionAD, BE and CF are altitudes of `triangle` ABC. If AD = BE = CF, prove that `triangle` ABC is an equilateral triangle.
View SolutionIn quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects `angle` ABC as well as `angle` ADC.
View SolutionIn `triangle ABC, AB gt AC` and D is any point of BC. Prove that, AB `gt` AD.
View SolutionIn `triangle ABC, AC gt AB`. AB is extended to P and AC is extended to Q. Prove that, `angle PBC lt angle QCB`.
View SolutionIn `triangle` ABC, AD, BE and CF are altitudes. Prove I, that, `AD + BE + CF lt AB + BC + CA`
View SolutionPoint S lies in the interior of A PQR. Prove that, SQ + SR `lt` PQ + PR.
View SolutionIn `triangle` ABC, AD is a median. Prove that AB + AC `gt` 2AD
View SolutionFor any triangle, prove that the sum of the sides of the triangle is greater than the sum of the medians of the triangle.
View Solution
SKILL TESTING EXERCISE questions and complete solutions for chapter TRIANGLES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9