Complete Solutions to EXERCISE (Subjective Problems) ( Short Answer Type) of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| MTG IIT JEE FOUNDATION | EXERCISE (Subjective Problems) ( Short Answer Type) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
If the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
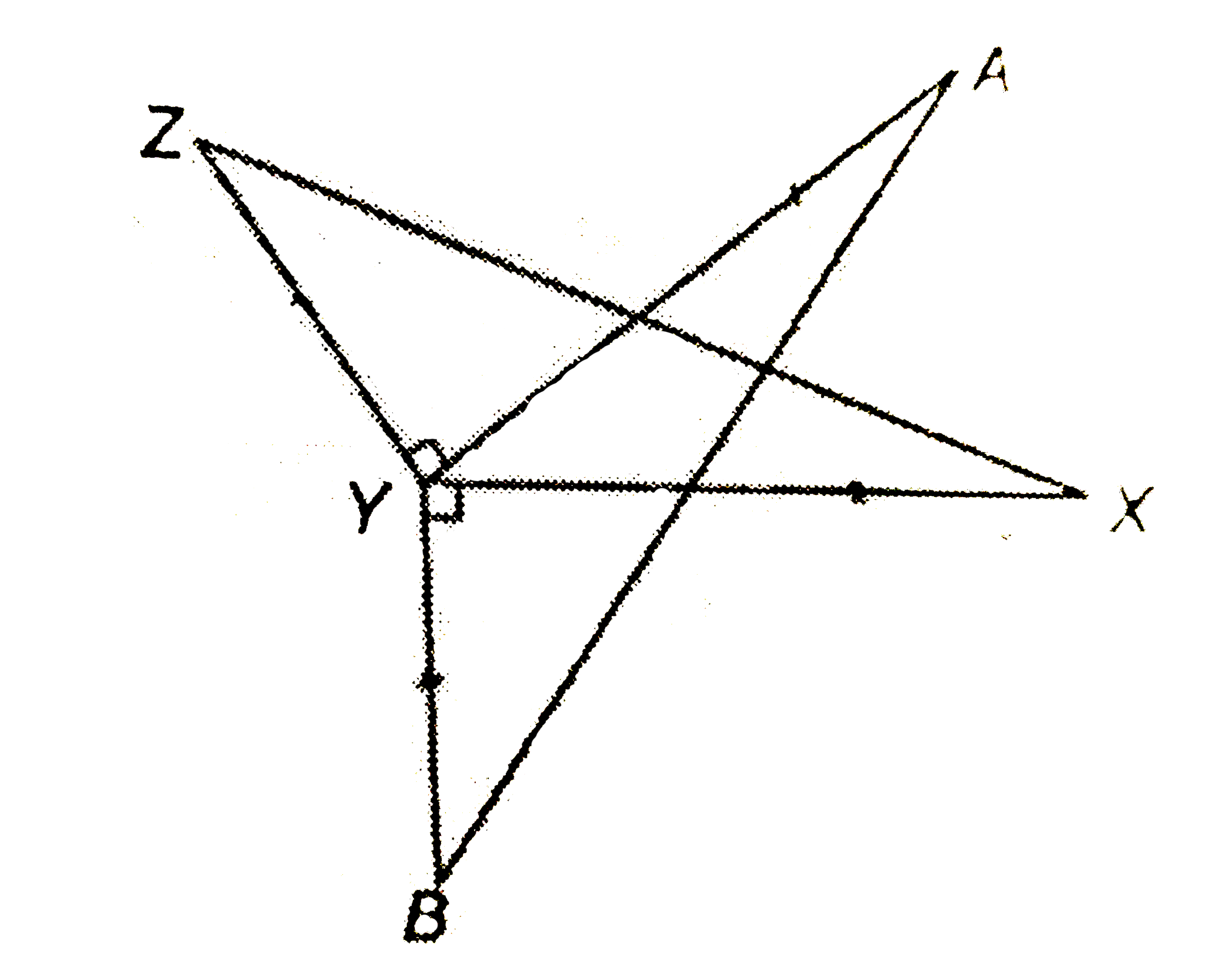
View SolutionIn the adjoining figure, `angleAYZ=angleBYX=90^(@), AY = YZ` and `XY = BY`. Prove that `AB = ZX`.
View SolutionIn the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.

View SolutionAB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P, prove that
`DeltaAPX~=DeltaBPY`
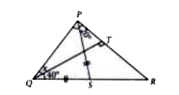
View SolutionIn the given figure, `QT bot PR` and QS = PS. If `angleTQR = 40^(@) and angleRPS = 20^(@)` then find value of x.
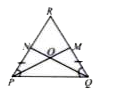
View SolutionIn the figure, `angleQPR = anglePQR` and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
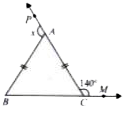
View SolutionIn the figure `AB=AC, angle ACM=140^(@) and anglePAB=x`. Find the value of x.
View SolutionIn the figure, show that `2(AC+BD) gt AB+BC +CD+ DA`.

View SolutionIn a right angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side.
View SolutionIn figure, it is given that `RT=TS, angle1=angle4 and angle3=angle2`. Prove that `DeltaRBT~=DeltaSAT`.
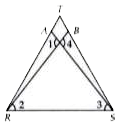
View Solution
EXERCISE (Subjective Problems) ( Short Answer Type) questions and complete solutions for chapter TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS TRIANGLES
- EXERCISE (Multiple Choice Questions) (ASSERTION & REASON TYPE)
- EXERCISE (Multiple Choice Questions) (COMPREHENSION TYPE)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
- EXERCISE (Multiple Choice Questions) (PASSAGE)
- EXERCISE (Subjective Problems) ( Integer/Numerical Value Type)
- EXERCISE (Subjective Problems) ( Long Answer Type)
- EXERCISE (Subjective Problems) ( Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 7.1)
- NCERT SECTION (Exercise 7.2)
- NCERT SECTION (Exercise 7.3)
- NCERT SECTION (Exercise 7.4)
- NCERT SECTION (Exercise 7.5)
- OLYMPAID/ HOTS CORNER
- SOLVED EXAMPLES