Complete Solutions to SOLVED EXAMPLES of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| MTG IIT JEE FOUNDATION | SOLVED EXAMPLES |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Prove that `DeltaABC` is isosceles if median AD is perpendicular to BC.
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

View SolutionIn figure it is given that `BC=CE and angle1=angle2`. Prove that `DeltaGCB~=DeltaDCE`.

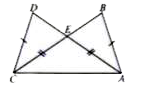
View SolutionIn the figure it is given that AB=CD and AD=BC. Prove that `DeltaABC~=DeltaCDA`.
View Solution`A B C D` is a parallelogram, if the two diagonals are equal, find the measure of `/_A B Cdot`
View Solution`A D ,\ B E\ a n d\ C F ,` the altitudes of ` A B C` are equal. Prove that ` A B C` is an equilateral triangle.
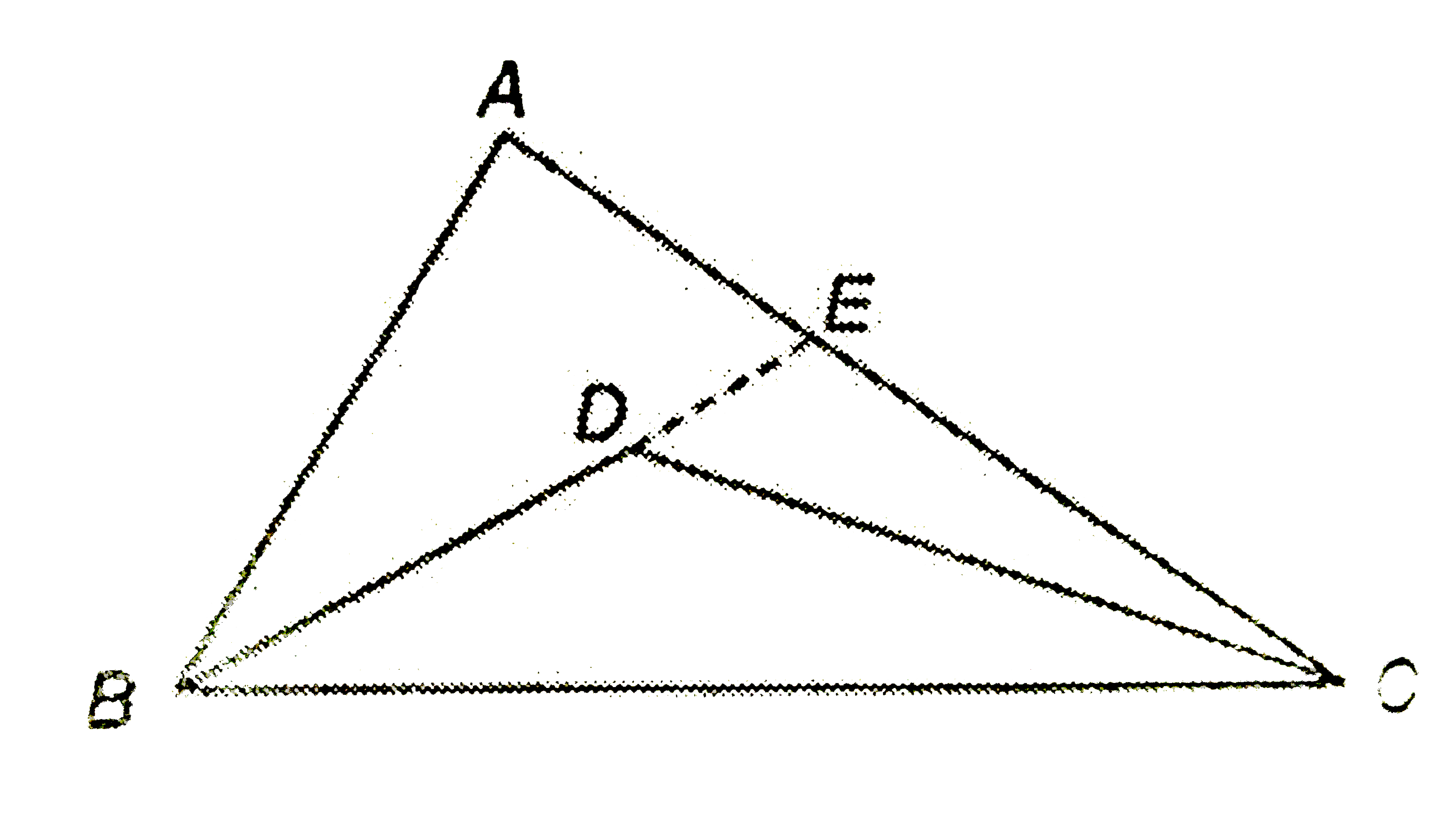
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that `BD+DC lt AB +AC`.
View SolutionIn the given figure, `AP_|_QR, PR gt PQ and PQ=PS`. Show that `ARgt AQ`.

View SolutionIn Figure, `A D` is a median and `B L ,\ C M` are perpendiculars drawn from `B\ a n d\ C` respectively on `A D\ a n d\ A D` produced. Prove that `B L=C M`
View SolutionSuppose line segments `A B\ a n d\ C D` intersect at `O` in such a way that `A O=O D\ a n d\ O B=O Cdot` Prove that `A C=B D` but `A C` may not be parallel to `B D`
View SolutionA point `O` is taken inside an equilateral four sided figure `A B C D` such that its distances from the angular points `D` and `B` are equal. Show that `A O` and `O C` are in one and the same straight line. GIVEN : A point `O` inside an equilateral quadrilateral four sided figure `A B C D` such that `B O=O Ddot` TO PROVE : `A O` and `O C` are in one and the same straight line.
View SolutionIn figure, prove that `(AM+BM+CM+DM) gt (AO+BO+CO+DO)`

View SolutionIn figure prove that
`MN+NO+OP+PM gt 2MO`

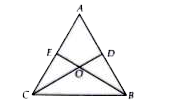
View SolutionIn figure, it is given that AE=AD and BD=CE. Prove that `DeltaAEB~=DeltaADC`.
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS TRIANGLES
- EXERCISE (Multiple Choice Questions) (ASSERTION & REASON TYPE)
- EXERCISE (Multiple Choice Questions) (COMPREHENSION TYPE)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
- EXERCISE (Multiple Choice Questions) (PASSAGE)
- EXERCISE (Subjective Problems) ( Integer/Numerical Value Type)
- EXERCISE (Subjective Problems) ( Long Answer Type)
- EXERCISE (Subjective Problems) ( Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 7.1)
- NCERT SECTION (Exercise 7.2)
- NCERT SECTION (Exercise 7.3)
- NCERT SECTION (Exercise 7.4)
- NCERT SECTION (Exercise 7.5)
- OLYMPAID/ HOTS CORNER
- SOLVED EXAMPLES